川西南下寒武统筇竹寺组页岩旋回地层学研究
2024-02-26周杨金思丁刘岩刘四兵张全林
周杨,金思丁,刘岩,刘四兵,张全林
1.成都理工大学能源学院,成都 610059
2.油气藏地质及开发工程全国重点实验室(成都理工大学),成都 610059
3.中石化西南油气分公司,成都 610041
0 引言
四川盆地筇竹寺组是寒武系页岩气的重要勘探目的层[1-2],是继志留系龙马溪组之后的又一页岩气勘探开发的热点层段,具有较好的勘探前景[3-4]。前人针对该层段沉积、层序地层方面做过诸多工作[5-8],但由于寒武系地层时代老,取心长度有限,区域上也缺乏可靠的古生物地层或年代地层等资料的约束,筇竹寺组地层的沉积旋回与充填过程至今尚不十分明朗,很大程度上制约了该层系页岩气的勘探进程。大量学者尝试对四川盆地及周缘地区的寒武纪地层进行了层序地层划分[9-11]。大多数划分方案都以典型露头剖面实测为基础,结合岩石薄片、钻测井、古生物、地球化学和地球物理等资料,通过对层序界面特征和层序内部充填样式的识别,建立年代地层、岩石地层与层序地层之间的联系。然而不同学者的层序划分方案和标准并未达成一致,尤其是没有利用统一的时间区间对层序进行分级。三级层序海平面升降的起源是过去30 年悬而未决的问题之一,目前被广泛接受的一种级别划分方式是将三级层序的形成归因为冰川型海平面变化的结果,并将三级层序的持续时限与海平面变化的周期相对应[12-13]。因沉积相类型多且变化快,无法通过某一个或几个剖面去追踪区内所有三级层序界面,前人对下寒武统泥页岩沉积地层的三级层序的划分存在一定不合理性。近年来,基于米兰科维奇理论的高频层序识别与划分已成为研究的热点和前沿领域[14-15],不仅成功应用于厘定地层沉积持续时间及判别重要地质事件的天文影响因素[16-19],并且通过提取天文周期曲线为参考曲线的方式,实现了深水页岩沉积的高频层序定量划分[20-22],该理论方法可以从成因上解决高频沉积层序单元的划分问题[23]。在解决页岩地层精细划分和对比的问题基础之上,可进一步实现页岩油气勘探有利层段的预测,对页岩油气勘探也具有重要意义。
国内在20 世纪90 年代初就开始利用测井资料进行旋回地层学研究[24],目前常规测井曲线(自然伽马、电阻率、密度、声波时差等)是最常使用的测井资料[25-27]。其中,自然伽马测井综合反映了沉积地层中放射性元素(钍、铀、钾)的含量,能够较好地反映岩性变化,尤其是地层中黏土矿物和有机质含量的变化,常被用作古气候替代指标[20,26,28];电阻率若仅受黏土矿物含量或有机质含量其中之一的单因素调控,亦能成为有效的古气候替代指标[29],例如:美国西部内陆盆地白垩纪Niobrara 组地层电阻率被认为与天文轨道驱动作用下的碳酸盐岩含量相关[30];位于佛罗里达海峡附近的钻探(航次166,站位1006)的声波曲线记录了1.4 m的天文强迫周期[31]。天文轨道周期驱动作用下的气候变化能对不同沉积组分产生相应的影响,且不同测井参数对古气候的响应方式不同[29,32],单一测井替代指标及划分标准不能同时适用于所有地层。
本次研究拟对四川盆地井研—犍为地区下寒武统筇竹寺组沉积地层开展旋回地层学研究。在考虑测井响应主控地质因素的前提下,以常规测井数据作为替代指标,并对测井数据进行多窗口频谱分析和相关系数分析,从地层中识别出可靠的米兰科维奇信号。通过长偏心率滤波和天文校准,建立金页1井的“浮动”天文年代标尺。根据沉积噪音模型DYNOT 曲线,从相对海平面变化周期的角度探讨筇竹寺组三级层序的划分方案,并根据已建立的天文标尺,估算各个三级层序的持续时间。最后,尝试以邻区梅树村剖面石岩头组底部CA-ID-TIMS U-Pb 定年结果(526.86±0.16 Ma)为年龄控制点,估算金页1井时间序列关键界面的年龄,并与2020 年国际地质年代表进行对比,验证本次旋回地层研究的准确性。
1 地质概况
1.1 古地理背景
四川盆地位于上扬子板块,是一个四面被造山带环绕的菱形叠合盆地,总面积为18×104km2(图1a)。震旦纪灯影阶至早寒武世麦地坪阶,上扬子地区发生了三幕桐湾运动[33],区域性隆升和间断性剥蚀作用使得岩相古地理极其复杂,由北西向南东的沉积环境展布为:古陆—滨海相—浅水陆棚相—深水陆棚相[34-35]。查明不同地区富有机质页岩段的等时对比关系是制约四川盆地页岩气勘探选区的关键地质问题,刘忠宝等[9]将上扬子下寒武统整体划分为8 个三级层序,其中筇竹寺阶发育4 个三级层序(图1b)。大量研究表明,四川盆地绵阳—长宁拉张裂陷槽在早寒武世充填了巨厚的深水陆棚相泥页岩[36],受裂陷槽影响,筇竹寺组泥页岩在资阳—宜宾一带地层横向发育稳定,无沉积间断且厚度大,较裂陷槽外部浅水陆棚及台地区更适宜开展旋回地层学工作。
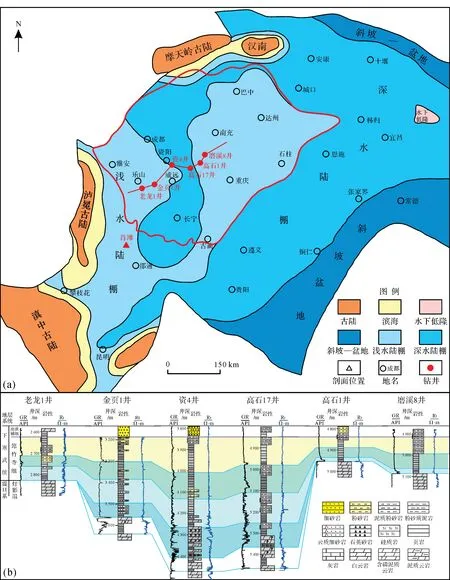
图1 (a)四川盆地及周缘地区下寒武统筇竹寺组岩相古地理平面图;(b)四川盆地下寒武统层序地层对比图Fig.1 (a) Lithofacies paleogeography of Lower Cambrian Qiongzhusi Formation in Sichuan Basin and the adjacent areas;(b) sequence stratigraphic correlation map of Lower Cambrian in Sichuan Basin
1.2 地层划分与年代地层
与全球寒武纪年代地层划分方案相对比,国内传统划分的下寒武统下部相当于纽芬兰统和第二统[37]。四川盆地及其周缘地区下寒武统自下而上划分为梅树村阶、筇竹寺阶、沧浪铺阶与龙王庙阶,其中四川盆地麦地坪组(下寒武统底部)大致对应的国际年代地层单位为纽芬兰统幸运阶与第二阶,筇竹寺组大致对应第二阶与第三阶[38-39]。四川盆地内该套沉积地层具有同时异相性,地层序列的时空变化极为复杂,岩石地层名称复杂且不统一[40](表1)。金页1 井在寒武系筇竹寺组沉积期时处于裂陷槽沉积中心附近,已经有许多学者对金页1井进行了较为丰富的层序、沉积研究[4-6,44-45],为我们的研究提供了宝贵的基础资料。通过前人对四川盆地下寒武地层的时间框架的搭建,可以初步判定金页1井筇竹寺组沉积于~529 Ma 至~521 Ma 之间(表1)。同时可将该钻井与东北部发表了丰富同位素和生物地层的肖滩剖面进行横向对比[41-43](图2a,b)。肖滩剖面石岩头组下段存在的一段黑色岩性标志层,在整个华南板块内部台地区域可以进行对比,金页1井筇竹寺组下段同样也发育这样一套黑色页岩(图2c),表明筇竹寺组底部与石岩头组底部位于同一沉积时期;金页1井麦地坪组白云岩和磷块岩可与肖滩剖面朱家箐组中谊村段的特征岩性进行对比,麦地坪组与筇竹寺组不整合接触,四川盆地麦地坪组与肖滩剖面寒武系早期朱家箐组处于同一沉积时期[52]。
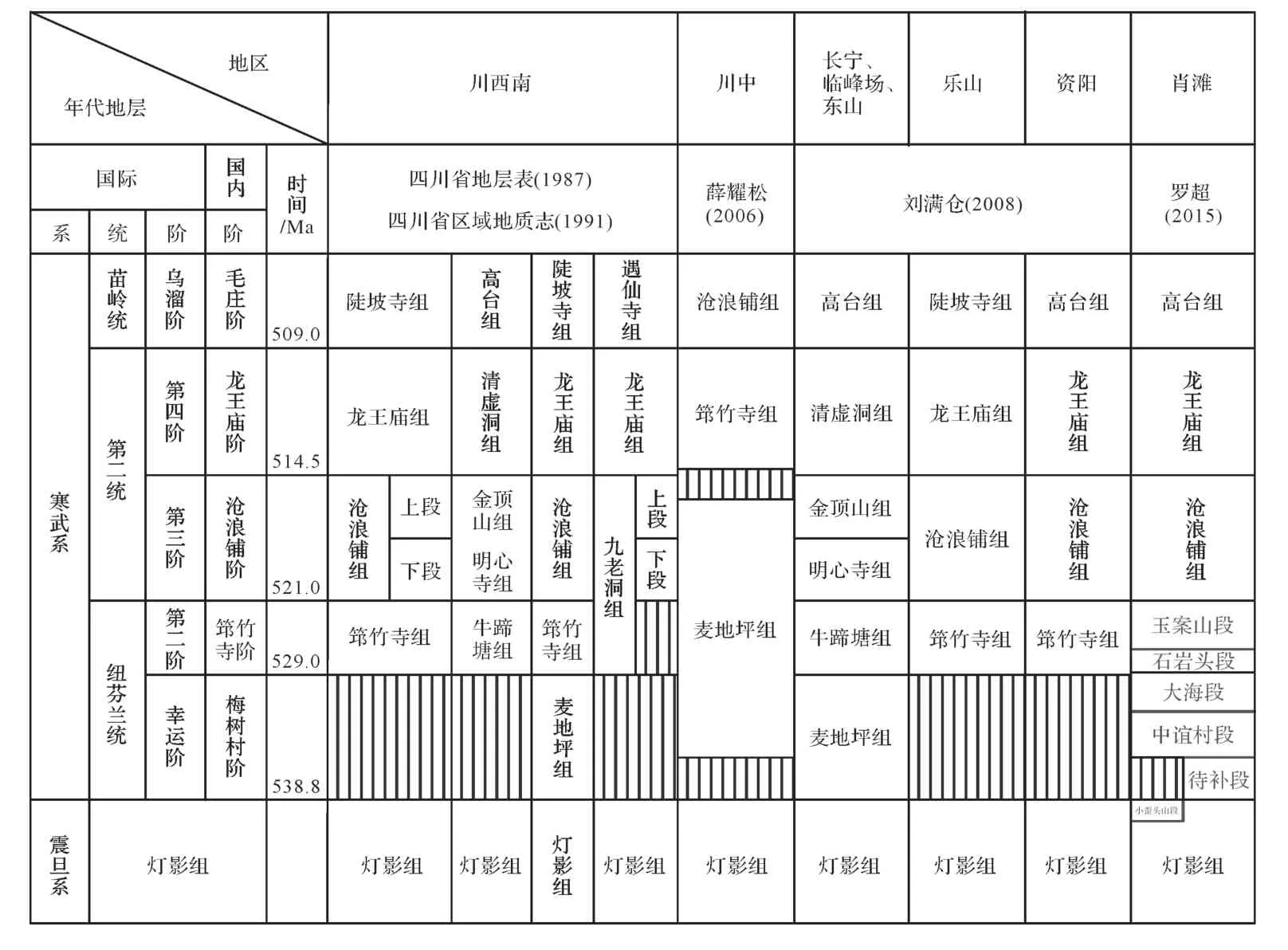
表1 四川盆地及周缘地区下寒武统地层与时间框架[40-43]Table 1 Stratigraphy and geological time scale of the Lower Cambrian in Sichuan Basin and the adjacent areas[40-43]
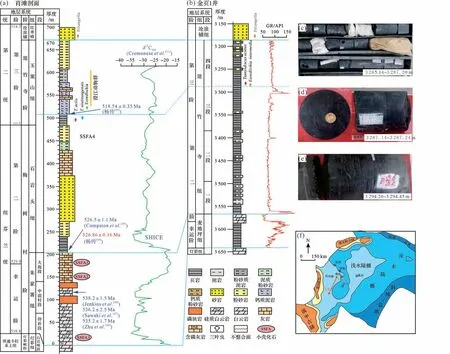
图2 金页1 井与肖滩剖面岩石地层、古生物地层和年代地层对比[46-51](a)肖滩剖面地层划分方案及年代地层学;(b)金页1井地层划分方案;(c~e)金页1井典型岩心照片及古生物照片;(f)钻井及剖面位置Fig.2 Correlated lithostratigraphy,biostratigraphy and chronostratigraphy between well Jinye-1 and Xiaotan section[46-51](a) stratigraphic and chronostratigraphic division of Xiaotan section;(b) stratigraphic division of well Jinye-1;(c-e) photographs of typical cores and paleontological specimens of well Jinye-1;(f) location of well Jinye-1 and Xiaotan section
2 数据与方法
本文的研究数据主要为金页1 井的常规测井和自然伽马能谱测井,除此之外,还包括TOC含量和黏土矿物含量的实测数据及测井曲线拟合数据。该钻井以寒武系筇竹寺组页岩层系为目的层,钻至下伏灯影组,本文研究主要选取3 184~3 655 m,采样间隔为0.1 m 的测井数据进行旋回地层学分析。在进行天文旋回分析之前,对各类测井数据采用滑动窗口相关分析(evolutionary correlation analysis),可根据其所显示的平面二维热力图,对测井曲线数值的相关程度以不同深度及不同地层厚度变化的角度进行了解[29],并通过测井响应特征分析,选取最佳测井序列作为旋回地层学的替代指标。
旋回地层学分析方法主要是时间序列分析方法,包括Multitaper method(MTM)频谱分析[53]、Fast Fourier transform(LAH)滑动窗口频谱分析[54-55]、滤波分析、相关系数分析(correlation coefficient 及evolutionary correlation coefficient)、沉积噪音模型(sedimentary noise model)分析等[56]。由于曲线包含各类地质因素引起的周期性变化,除了一些与地质因素无关的干扰信号之外,还包括一些长周期引起的高频信号,在进行频谱分析之前,要将这种信号通过去趋势化的方法去除[57],去趋势化(detrended)的测井序列中受天文周期影响的信号将更突出。本次研究的所有计算使用的软件包为基于Matlab平台下的AcycleV2.4[58]。
3 测井响应特征分析
测井响应特征分析是利用测井资料进行地质分析的基础。古环境、古气候的变化对不同测井数据影响的差异,决定了不同测井资料是否能够解决相关古气候古环境问题。自然伽马(GR)测井的数值主要取决于地层中自然伽马辐射的强度,主要受地层中Th、U、K元素的分布与聚集的影响。K和Th的含量与黏土矿物含量关系密切,在风化和黏土矿物形成过程中,Th 元素具有有限的流动性,比K 更不容易溶解,完全存在于碎屑组分内。前人研究表明,Th 和K 的比值可以较好地反映碎屑颗粒的粒度大小,从而指示当时水体环境的能量大小[59]。Th 和U 的比值能够反映沉积水体的氧化还原条件[60],随着水体还原程度的逐渐增加,Th/U 值逐渐减小。一般而言,Th/U 小于4为强还原环境,大于4且小于10指示还原环境,大于10 指示氧化环境[61]。在具有很高的U 值,而Th、K 数值较低的层段,随U 值增高,Th、K 数值并未相应增大,可能是流体滤液十分活跃所离析的铀矿物附着于裂缝中所引起的。另外,U含量与氧化还原条件密切相关,还原环境下,有机质含量高,对应的U含量高。
金页1井筇竹寺组(3 184~3 566 m)的GR、U元素测井曲线具有相似的变化特征,而Th 元素和K 元素测井曲线变化趋势则与GR、U元素曲线明显不同(图3),推测U元素主要形成于后生成岩作用,自生铀在还原条件下的富集作用引起部分层位出现的高U值。与此同时,滑动窗口相关分析图显示(图4),GR曲线与Th、K元素含量的相关性整体上是正相关,但在较大部分的深度段相关系数都低于0.5,如3 303 m,3 384 m,3 496 m 深度附近,滑动窗口大小20 m 左右的热力图中相关系数的读数约为0.2,不具有相关性。而GR 曲线与U 元素含量整体上不具有明显的相关性,相关系数在热力图中的读数为0.2 左右,但在3 303 m,3 402 m,3 566 m深度附近,相关系数数值接近1.0,显示出强烈的正相关,推测是地层中放射性元素的非气候成因富集导致的异常高GR和高U值。因此,GR 和U曲线并不能很好地反映同沉积时期的沉积环境,不是天文旋回研究的有效古气候替代指标。由于Th 和K 元素都和碎屑黏土密切相关,所以黏土矿物含量与Th、K元素含量显示出明显的正相关性,从另一个角度证明自然伽马能谱测井曲线中的Th、K元素含量能够很好地反映古气候、古环境变化,可以作为金页1 井沉积地层的天文旋回研究的良好替代指标。Th/K与黏土矿物含量的相关性,不如Th、K元素与黏土矿物含量的相关性显著(图4),部分层段表现为负相关(3 303 m,3 566 m),这可能是由于K元素含量对黏土矿物含量的影响要高于Th元素。

图3 金页1 井筇竹寺组(3 184~3 566 m)测井曲线特征Fig.3 Logging characteristic of well Jinye-1,Qiongzhusi Formation (3 184-3 566 m)
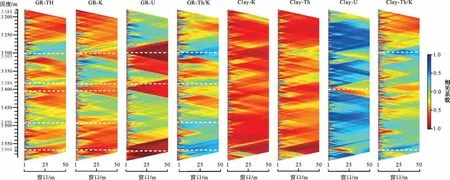
图4 金页1 井筇竹寺组伽马能谱测井相关分析Fig.4 Correlation analysis of natural gamma spectrometric logs in well Jinye-1,Qiongzhusi Formation
由于Th 元素和K 元素对古气候的响应机理类似,在偏心率较大的地质历史时期,相对温暖湿润的气候条件增加降水、化学风化强度等,导致沉积颗粒粒径减小,黏土矿物沉积量增加;升高的黏土矿物含量通常对应于的高Th和高K值,高Th和K值被认为与高偏心率的地质历史时期对应,本文采用K 元素含量作为旋回地层学的替代指标。在3 303 m,3 384 m,3 496 m等深度段测井数据均出现了较为明显的变化(图3,4)。为了分析不同沉积环境的测井响应特征,分别对这四个深度段进行测井值统计分析(图5)。可以看出在筇竹寺组的四段地层中,各类测井曲线的均值和方差都发生了明显的变化,指示出筇竹寺组页岩沉积环境及沉积速率在这四段沉积地层中发生了明显变化。
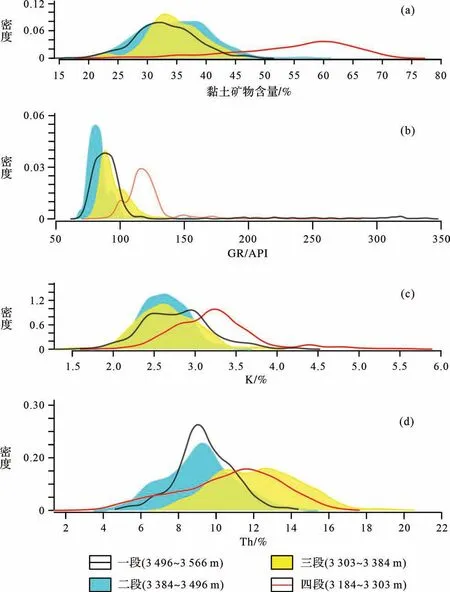
图5 金页1 井筇竹寺组不同层段伽马能谱测井响应特征统计Fig.5 Density plots of different layers natural gamma spectrometric logging in well Jinye-1,Qiongzhusi Formation
4 旋回地层学分析
4.1 寒武纪早期的天文轨道周期
由于太阳系内的行星混沌作用贯穿始终,50 Ma以前的地层并没有高精度的天文年代学校正[62]。寒武纪早期的天文轨道周期不同于运用在比较新的地层中20∶5∶2∶1的周期比值,斜率和岁差会更接近,部分叠置难以识别;且短偏心率周期与斜率周期也可呈4∶1的比值关系,与长偏心率与短偏心率4∶1的比值相同,而造成多解性。目前有三种轨道周期方案试图通过建立相对准确的地月系统演化模型来确定较老的地层的天文周期信号[63-64]。本次研究采用Waltham[65]解决方案,认为405 kyr长偏心率周期在地质历史时期内保持稳定不变,以同时代古潮汐韵律计地球自转速度建立月球撤退模型计算出520 Ma 左右的天文轨道周期为405 kyr,131 kyr,95 kyr,36.4 kyr,28.2 kyr,20.4 kyr,19.4 kyr,16.8 kyr。
4.2 深度域频谱分析
未做处理的K元素测井曲线存在随深度增大先减小,随后又增加的趋势(图3),这可能是长周期的构造演化所产生的信号,也有可能是测井曲线在原位地层中受地层温度、压力的影响所导致的与天文周期无关的旋回信号。前人研究表明,该沉积地层的沉积速率在2~5 cm/kyr[66],长偏心率周期(405 kyr)控制的沉积旋回厚度为8~20 m,因此本次研究中去趋势化处理采用的窗口大小为30 m,用于保留天文轨道长偏心率周期。
对趋势化后的K元素测井数据进行滑动窗口频谱分析(图6a),滑动窗口步长为0.7 m,窗口长度为30 m。图谱中峰值所对应的深度(频率的倒数)表明各个深度段均保存了长偏心率、短偏心率及斜率的信号,岁差信号不明显。然而,谱图中峰值所对应的频率在3 303 m,3 384 m 和3 496 m 处同样出现了明显的峰值信号不连续现象(图6a),是由于某些深度段的测井序列中包含更多的噪声,高频信号被具有更高功率的噪声所抑制[67],也可能是由于沉积速率的变化导致沉积周期发生了变化[68]。综合考虑滑动频谱图谱上出现信号不连续的深度(图6a),及测井响应特征(图4,5)发生变化的深度,将整个筇竹寺组(3 184~3 566 m)划分为四个层段,从下到上依次为:一段(3 496~3 566 m),二段(3 384~3 496 m),三段(3 303~3 384 m)和四段(3 184~3 303 m)(图6b~e),并分别进行频谱分析。在筇竹寺组一段地层中(图6b),高于90%置信度的6 个频率谱峰对应的厚度周期为10.44,3.68,2.53,1.34,1.08 和1.01 m;筇竹寺组二段地层(图6c),高于90%置信度的6 个频率谱峰对应的厚度周期为18.86,6.25,4.52,2.43,1.70 和1.70 m;筇竹寺组三段地层(图6d),高于90%置信度的7个频率谱峰对应的厚度周期为11.76,5.71,3.41,2.34,1.21和0.87 m;筇竹寺组四段地层(图6e),高于90%置信度的7 个频率谱峰对应的厚度周期为13.33,4.64,3.21,2.51,1.40和1.01 m。筇竹寺组内划分的四个层段识别的部分显著周期均和405∶131∶95∶36.4∶28.2的比值相接近,证明筇竹寺组四段地层沉积时期均受到米兰科维奇旋回的影响。由于沉积环境在不同层段发生了改变,沉积速率发生了微小变化,此处通过长偏心率周期(405 kyr)对应的沉积厚度,对每段沉积速率进行一个初步估计:一段沉积速率约为2.46 cm/kyr,二段沉积速率约为4.65 cm/kyr,三段沉积速率约为2.90 cm/kyr,四段沉积速率约为3.28 cm/kyr。金页1 井筇竹寺组的沉积速率呈现先增大后减小,随后又增大的趋势。

图6 金页1 井筇竹寺组(3 184~3 566 m)K 元素曲线频谱分析图(a)3 184~3 566 m滑动窗口频谱分析;(b)3 184~3 303 m 频谱分析;(c)3 303~3 384 m频谱分析;(d)3 384~3 496 m频谱分析;(e)3 496~3 566 m频谱分析Fig.6 Spectral analyses of K logging series in the Qiongzhusi Formation (3 184-3 566 m) in well Jinye-1(a) evolutionary spectral analysis of 3 184-3 566 m;(b) spectral analysis of 3 184-3 303 m;(c) spectral analysis of 3 303-3 384 m;(d) spectral analysis of 3 384-3 496 m;(e) spectral analysis of 3 496-3 566 m
4.3 最优沉积速率的估算
通过频谱分析,在90%的置信度之上检测到了周期性变化的功率,但所选取的K 元素测井曲线的数据是以深度为单位,在对应的沉积时间范围内并没有进行频率计算。因此,本文通过“COCO(correlation coefficient)”和“eCOCO(evolution correlation coeffi cient)”[57]两种方法分析,将深度序列的替代指标转换成时间序列,然后计算该时间序列的功率谱与天文解决方案功率谱之间的相关系数,从而提高旋回识别的准确性(图7)。本次研究的“COCO”计算得出金页1 井筇竹寺组的平均沉积速率在2.5,2.9,3.4 和4.8 cm/kyr 处的H0显著水平(被错误拒绝的零假设,即非天文轨道驱动信号)都低于0.001,且参与计算的天文轨道参数分量多于6个。本次研究的eCOCO分析选取1~6 cm/kyr 的沉积速率区间,滑动步长为0.5 m,滑动窗口为30 m,蒙特卡洛模拟2 000次,得到图7所示结果,其中红色(极值)决定了特定深度的最优沉积速率。

图7 金页1 井筇竹寺组深度序列(3 184~3 566 m)的COCO 分析和eCOCO 分析结果Fig.7 “COCO”and“eCOCO”analyses of the Qiongzhusi Formation depth-rank series in well Jinye-1 (3 184-3 566 m)
根据频谱分析,用比值法对不同深度段的平均沉积速率的初步估算(2.46 cm/kyr,4.65 cm/kyr,2.90 cm/kyr 和3.28 cm/kyr),与用检验法(eCOCO)对最优沉积速率的评价的结果相一致,再次证明本次研究选取的功率谱频段组合是满足天文轨道驱动条件的。
4.4 滤波和调谐
基于频谱分析及COCO、eCOCO 分析的结果,将代表长偏心率(E,405 kyr)的沉积旋回通过高斯带通滤波提取出来。其中,筇竹寺组一段的滤波频率为0.10±0.02 cycles/m,二段的滤波频率为0.053±0.009 cycles/m,三段的滤波频率为0.085±0.015cycles/m,四段的滤波频率为0.075±0.001 cycles/m(图8)。滤波结果显示金页1井筇竹寺组总共记录了29个长偏心率周期,其中:一段(3 496~3 566 m)记录了约7 个长偏心率旋回;二段(3 384~3 496 m)记录了6 个长偏心率旋回;三段(3 303~3 384 m)记录了7 个长偏心率旋回;四段(3 184~3 303 m)记录了9 个长偏心率旋回(图8c)。本次研究选取代表长偏心率的滤波曲线建立深度—时间模型,从而得到时间域数据序列,并结合对应的深度域序列获得金页1 井筇竹寺组连续变化的沉积速率曲线(图8d)。在3 303 m,3 384 m 和3 496 m 处沉积速率出现了明显的变化,整个筇竹寺组沉积时期,由下到上呈现先增大后减小的趋势。
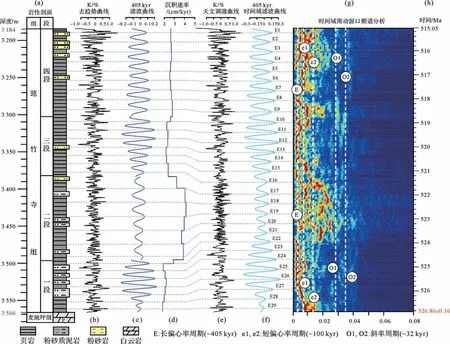
图8 金页1 井筇竹寺组K 元素曲线滤波、调谐、时间域滑动窗口频谱分析和浮动天文年代标尺(a)岩性剖面;(b)去趋势化的K元素测井曲线(深度域);(c)K元素405-kyr滤波曲线(一段频率:0.10±0.02 cycles/m,二段频率为0.053±0.009 cycles/m,三段频率为0.085±0.015 cycles/m,四段频率为0.075±0.001 cycles/m);(d)沉积速率变化曲线(深度域);(e)调谐后的K元素测井曲线(时间域);(f)时间域K元素测井曲线405-kyr滤波曲线;(g)时间域K元素测井曲线滑动窗口频谱分析;(h)浮动天文年代标尺Fig.8 Filtering,tuning,evolutionary spectra analysis and floating astronomical time scale of K logging series in well Jinye-1(a) lithological profile;(b) de-trended K series in depth domain;(c) 405-kyr filtered K series in depth domain (bandpasses of the four sections: 0.10±0.02,0.053±0.009,0.085±0.015 and 0.075±0.001 cycles/m respectively upwards from bottom);(d) sedimentation rate in depth domain;(e) 405-kyr tuned K series in time domain;(f) 405-kyr filtering curve in time domain;(g) evolutional spectra analysis of tuned K series;(h) floating astronomical time scale
4.5 “浮动”天文年代标尺的建立
以筇竹寺组底部年龄526.86±0.16 Ma 作为天文年代调谐的初始锚点,界定本次研究的时间范围,建立“浮动天文年代标尺”(图8h)。为了验证滤波和调谐结果的准确性,对用天文校准后转化成时间域的数据序列再次进行滑动窗口频谱分析(图8g),结果显示识别的频率有0.002 5,0.007 6,0.010 5,0.027 8,0.038 5 cycles/kyr,在405 kyr(长偏心率期),131 kyr(短偏心率周期),95 kyr(短偏心率周期),36 kyr(斜率周期),28 kyr(斜率周期)的位置上有较强的功率谱,验证了天文调谐的结果是可靠的。在岁差频率上由于沉积速率较低和数据分辨率不够等问题,没有获得较明显的天文信号。
5 基于米兰科维奇理论的层序地层划分
传统的层序地层学研究多应用于盆地边缘的沉积序列中,基于等时的角度研究地层叠加样式及其变化[69],层序地层学的发展极大地完善了与海平面变化相关的沉积物堆砌样式的解释,并通过建立等时地层格架,来重建地质历史时期的海平面变化[70-71]。然而,对于盆地中心的深水沉积物,某些“不整合面”可能是非常细微尺度的,甚至是“整合的”,很难通过传统的层序地层学研究方法进行识别。基于米兰科维奇理论的旋回地层学,以地球轨道周期为“成因”控制,对细粒沉积地层进行定量分析,可以利用天文周期的时间属性约束不同级次的海平面变化旋回,从而进行高频率层序地层划分。
5.1 沉积噪音模型
Liet al.[56]开发的沉积噪音模型(DYNOT和ρ1)是一种基于轨道调谐后的动态沉积噪音模型,也被证明是一种有效的海平面变化重建方法[56,72-73]。沉积岩中不同气候替代指标保存的信息包括“信号”(即轨道周期作用下的产物和“噪声”和无轨道控制作用的影响因素),如定年误差、差异压实、不稳定沉积和成岩作用等,在固定位置与水深有关的噪声的变化可能与海平面的变化有关。当海平面相对较高时,与水深相关的噪声相对较低,反之亦然。选取DYNOT模型中功率谱中非轨道方差的比值,用于度量气候和海平面替代指标中的噪声;如果与替代指标相关的噪声比较小,噪声的方差可以作为海平面相对变化的指标,在滑动时间窗口中计算出非轨道信号方差和总方差的比值,即DYNOT 值;当相对海平面较高的时候,DYNOT 较低,反之亦然[56]。DYNOT 模型之外的补充模型——独立的lag-1 自相关系数模型,即ρ1 模型,作为相对海平面变化的第二个独立噪声指标进行检验,噪声的增加会导致ρ1 值的降低,反之亦然[56]。基于沉积噪音模型的假设和计算,本文通过对K 元素时间序列进行沉积噪声曲线重建,获得两条能够替代同沉积时期相对海平面变化的曲线:DYNOT 和ρ1 曲线(图9f,g)。金页1 井筇竹寺组沉积时DYNOT 和ρ1 曲线呈现相似的模拟结果,整个沉积时期有9 处(图9 蓝色条形填充)显著增强的噪声(低信噪比)均出现在eCOCO 图谱中相关系数的低值区,即相对浅水、不稳定的沉积环境导致了噪声的增加,亦从另一个角度反映了相对海平面处于下降阶段。

图9 金页1 井筇竹寺组沉积噪音模型与相对海平面变化解释[51,74](a)岩性剖面;(b)去趋势化的K元素测井曲线(深度域);(c)深度域ρ1曲线;(d)eCOCO滑动窗口相关系数分析(深度域);(e)调谐后的K元素测井曲线和405 kyr滤波曲线(时间域);(f)DYNOT模型及DYNOT中值曲线的2.4 Myr滤波曲线(时间域);(g)ρ1模型(时间域);(h)全球海平面变化(GTS2020);(i)碳同位素变化曲线;(j)层序地层划分Fig.9 Sedimentary noise model and interpretation relative sea-level changes in well Jinye-1[51,74](a) lithological profile;(b) de-trended K series in depth domain;(c) ρ1 curve in depth domain;(d) eCOCO and sedimentation rate in depth domain;(e) 405 kyr tuned K series(black line) and 405 kyr filtering curve (red line) in time domain;(f) DYNOT model in time domain;(g) ρ1 model in time domain;(h) global sea-level change in GTS2020;(i) δ13C curve;(j) sequence stratigraphic division
5.2 层序地层划分
三级层序海平面波动的驱动机制长期以来备受争议,但越来越多的地质证据表明天文轨道周期通过调制气候波动来控制海平面的变化[75-78],长斜率周期(1.2 Myr)和长偏心率周期(405 kyr)控制着三级层序海平面波动及四级层序海平面波动。对旋回地层学与经典层序地层学的研究,在受海平面变化控制的成因和机理上有相似之处,天文旋回的时间内涵可以标定地质年代,可以作为层序划分的时间标尺。
前人针对页岩的层序地层研究,主要运用T-R旋回理论基础作为层序发育的主控因素,即海退旋回(R)和海进旋回(T)[79-80]。本次研究利用沉积噪音模型的计算,根据DYNOT和ρ1模型所指示的相对海平面变化特征,将筇竹寺组划分为4个三级层序和4个T-R旋回(图9j)。值得指出的是,本文通过对K元素深度域测井序列进行滑动窗口频谱分析(图6),及eCOCO进行最优沉积速率估算的同时(图7),通过找出的功率图谱上出现变化的深度值,将整个数据区间划分为四个段分别进行滤波,最后调谐得出的时间域曲线在这四段内具有明显不同的沉积速率,故此时的4 个三级层序与前文所划分的4 段地层是一一对应的。其中,4 个层序界面均发育于DYNOT 模型中值曲线的高值区,及对应ρ1模型中值曲线的低值区,代表相对海平面下降到最低点,发育层序边界,沉积速率发生改变;4个最大海泛面位于海进旋回T和海退旋回R之间,和DYNOT模型中值曲线的低值区及ρ1模型中值曲线的高值区相对应,代表了相对海平面升高至最大值。结合“浮动”天文年代标尺,SQ1三级层序对应地质年代处于526.86~523.68 Ma,SQ2 对应523.68~521.65 Ma,SQ3 对应521.65~518.68 Ma,SQ4对应518.68~515.05 Ma,得出每个三级层序的沉积时限分别为3.18,2.03,2.97 和3.63 Ma,分别包含8 个,5 个,7 个和9 个长偏心率(405 kyr)周期。405 kyr 的长偏心率旋回的变化常常与四级层序存在成因联系[81],2.4 Myr 周期通过地球和火星的天文共振而形成,也是三级海平面变化旋回的共有周期。图9f显示的DYNOT中值曲线的2.4 Myr滤波曲线呈现出4.5个2.4 Myr 变化周期,同时证明相对海平面变化受到2.4 Myr的三级海平面变化旋回的调控作用。
5.3 碳同位素漂移
寒武纪发生了多次碳同位素漂移事件,碳同位素异常事件在寒武系等的划分和对比中有着广泛的应用[26]。根据所建立的天文年代标尺,将全球无机碳同位素曲线[51]与相对海平面变化曲线[82]进行对比(图9i)。发现ZHUCE 正异常对应着相对海平面的高值区,SHICE 负异常对应着相对海平面的低值区,SHICE 之上的两次明显正异常均对应着相对海平面的极高值。推测可能是因为随着海平面下降,大量有机质被氧化,向海水中释放碳同位素偏轻的无机碳,造成海水中的δ13C 变轻[83]。Cremoneseet al.[51]在对肖滩剖面的有机碳同位素(δ13Corg)研究中识别了SHICE碳同位素漂移事件(图2),δ13Corg组成的影响因素众多,不同剖面相同层位之间δ13Corg曲线变化巨大,时常出现δ13Ccarb组成与δ13Corg组成不同步变化的情况,在肖滩剖面的δ13Corg曲线中未能识别其他碳同位素异常事件。
6 结论
(1)对四川盆地金页1 井筇竹寺组地层进行了测井曲线的响应特征分析,选取K 元素序列为相对最合适的替代指标,并按测井曲线的不同特征筇竹寺组地层分为四段进行频谱分析和滤波分析。发现目标层段记录的天文轨道控制作用下的沉积周期分别为405 kyr,131 kyr,95 kyr,36 kyr,28 kyr;根据长偏心率周期的天文校准建立了连续约11.8 Myr 的 “浮动”天文年代标尺。
(2)通过轨道调谐后的沉积噪音模型,恢复了沉积时期的相对海平面变化。根据DYNOT和ρ1曲线,将筇竹寺组划分为4个三级层序,识别了对应的4个层序界面和4 个最大海泛面,证明了405 kyr 的长偏心率旋回与四级层序存在成因上的联系。
(3)通过相对海平面变化曲线与全球性碳同位素漂移曲线的对比,发现海平面下降往往对应着碳同位素的负异常,推测是由于海水下降导致的有机质氧化,从而轻碳富集。
