基于GA-BPANN的钻井机械钻速预测模型

李 博，王鲁朝

（山东省第三地质矿产勘查院，山东烟台 264000）

随着我国经济的快速发展，资源、环境等问题变得越来越突出，科学钻探及矿产勘查等工作，都在持续不断地向深部延伸以解决上述矛盾[1-2]。然而，在钻探过程中，机械钻探速度对施工工期和经济效率有巨大关系，因此有较多学者针对机械钻探速度进行研究，取得了一些重要成果。早在1974 年，Bourgoyne 和Young（B＆Y）建立了一个数值模型，将机械钻速分析为八个因素的函数，包括(F1)地层强度的影响，(F2)地层正常压实的影响，(F3)地层欠压实的影响，(F4)压差的影响，(F5)钻头直径和钻头重量的影响，(F6)转速的影响，(F7)齿磨损的影响和(F8)钻头水力学的影响。B＆Y模型已被用作提高钻井效率的标准和可靠的方法[3-4]。然而，一些研究表明，由于缺乏多元回归技术，如回归点数量的敏感性和多重共线性的存在，B＆Y模型无法准确预测和模拟具有有意义常系数值的钻井行为。国内外传统统计分析建立地层可钻性模型的方法主要有dc指数模型法[5]、分形理论法[6-7]、测井参数计算法[8-12]和基于机械钻速的地层可钻性分级法[13-15]。然而，传统统计建模分析方法虽然考虑了较多因素的影响，但是在复杂地质钻进过程中由于各因素之间经常存在强耦合现象，导致其模型预测具有较大误差。针对复杂地质钻进过程中存在的不确定性、时变时滞和各变量之间强耦合等特性，运用机器学习方法是解决复杂地质钻进过程中进行机械钻速预测的有效途径。然而，针对碳酸盐岩地质基于机器学习方法预测机械钻速方面仍鲜有研究和报道。

本文建立了碳酸盐岩钻井机械钻速的支持向量回归（SVR）、BP人工神经网络（BPANN）和遗传算法优化BP 人工神经网络（GA-BPANN）三种机器学习预测模型，以期得到一种快速便捷的机械钻速预测方法，为碳酸盐岩地质钻井作业决策提供依据。

1 机器学习方法简介

1.1 支持向量回归（SVR）

支持向量回归在高维空间中构造超平面或超平面集合，将有限维空间映射到维数更高的空间中，从而可以同时最小化经验误差和最大化几何边缘区，直观的来说，分类边界离最近的训练数据点越远越好，因为这样可以缩小泛化误差[16]。值得注意的是在间隔边界之内的数据并不进行误差计算，即认为只有在间隔边界之外的数据才进行误差计算，在找到一个最优超平面的基础上，进一步确定一个在最优超平面上下范围内的空间，这个空间即为支持向量回归的结果[16]。

1.2 GA-BPANN神经网络

传统BPANN神经网络在进行模型训练时，其初始权重和偏置通常随机产生，但是如果初始权重和偏置选取不合理，极易导致神经网络模型的学习速率过慢而难以达到收敛，甚至会陷入局部最优的情况。

在确定BPANN神经网络结构后，通过遗传算法对神经网络进行优化，首先对BPANN神经网络各层间的初始权重和偏置进行实数编码，再经过选择、交叉、变异等遗传操作获取较优值，并将其作为BPANN神经网络的初始权重和偏置。遗传算法个体基因位数等于BPANN神经网络权重和阈值的个数，每位个体的适应度函数根据训练误差进行设计[17]，计算公式如下：

式中：f(i)——第i个染色体的适应度值；

p——神经网络训练样本数；

yij——第i个染色体对第j个样本的预测输出值；

tij——样本实际输出值。

2 碳酸盐岩钻井钻速的智能预测模型

2.1 输入数据

本文实例数据来自汶川地震断裂带科学钻探工程的主孔之一，位于四川省都江堰市虹口乡八角庙六组境内，钻井井位位于小沟山沟谷底的简易公路与河流之间的河床上，钻井位置海拔高度约1150m，工作区处于龙门山中央断裂带，井口距断裂带地表露头约650m。钻孔设计和实际钻孔结构和套管程序分别如图1（a）、（b）所示。

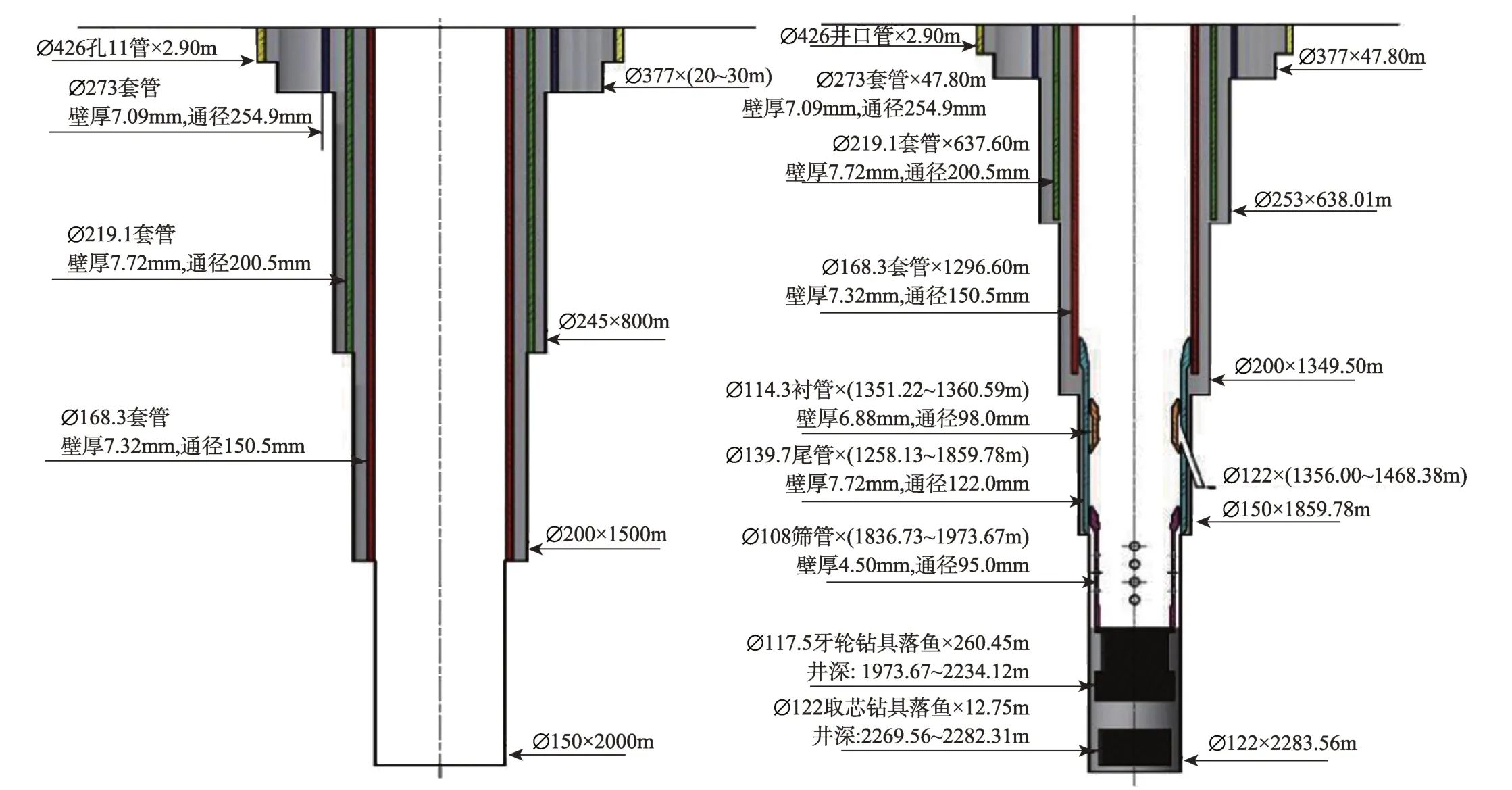
图1 钻孔结构和套管程序

收集的数据包括钻时、钩载、钻压、泵压、流量、转速、扭矩和总池体积，部分数据资料如表1所示。完整数据可在地质云网站中获取（https://geocloud.cgs.gov.cn/）。

表1 部分钻井数据

为了降低数值大小对模型精准度的影响，在进行训练模型时将表1中的数据，需要对各列数据进行归一化处理，如式（2）所示：

式中：x′i——归一化的数值；

xi——原始数值；

xmin——数值最小值；

xmax——数值最大值。

2.2 MIC相关性分析

MIC 的想法是针对两个变量之间的关系，将其离散在二维空间中，并且使用散点图来表示，将当前二维空间在x、y方向分别划分为一定的区间数，然后统计当前的散点在各个方格中落入的情况，即联合概率的计算，从而解决了在互信息中的联合概率难求的问题。MIC的计算公式如下式所示。

其中，X、Y是x、y方向上的网格划分个数，B是常数，通常取约m0.6。p(X,Y)为变量x和y之间的联合概率。

从图2可以看出，机械钻速与各因素的相关性均大于1/m（其中，m为模型输入变量的个数，此处m=9），说明各因素对机械钻速存在一定的影响。机械钻速与井深、钩载、钻压、流量、转速和扭矩的MIC值较大，说明这些因素对机械钻速的影响较高。然而，机械钻速与泵压和总池体积的MIC值较低，说明这两个因素虽然也会对机械钻速产生影响，但是影响程度较低。因此，本文选取MIC值较大的6 个影响因素作为输入变量，分别为井深、钩载、钻压、流量、转速和扭矩。

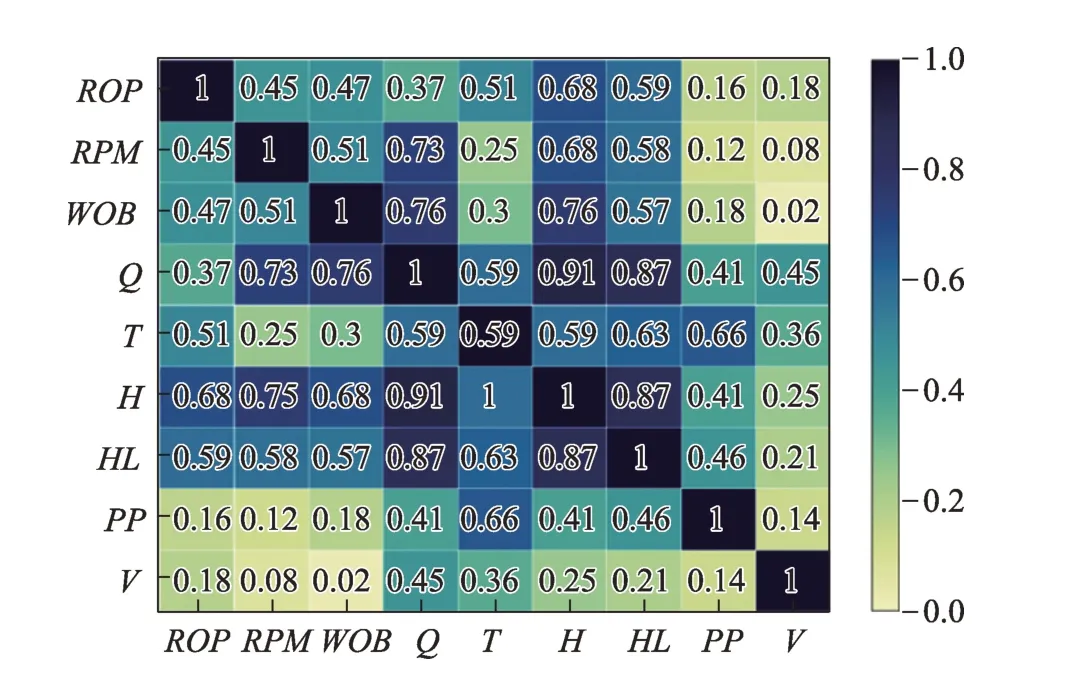
图2 钻井因素MIC值热力图

2.3 GA-BPANN神经网络结构参数设计

本文利用Python 工具箱进行BPANN 神经网络结构参数设计，其关键是确定BPANN 神经网络层数、隐藏层神经元个数和激活函数等方面[17]。

（1）BPANN 神经网络层数。研究表明，当单隐藏层无法达到预期效果时，可以通过适当增加隐藏层数来提高精准度，然而隐藏层数目过多会导致网络的复杂度增加，因此隐藏层一般不超过两层[17]，即隐藏层数目设为imin=1，imax=2。为了提高模型的预测精度本文隐藏层数目设置为2层。

（2）隐藏层神经元个数。通常采用试错法确定隐藏层神经元个数，神经元个数可由经验公式获得参数设置范围：，其中δ＝1，2，…，10。

采用上述原则及试错法确定的预测模型参数如表2所示。

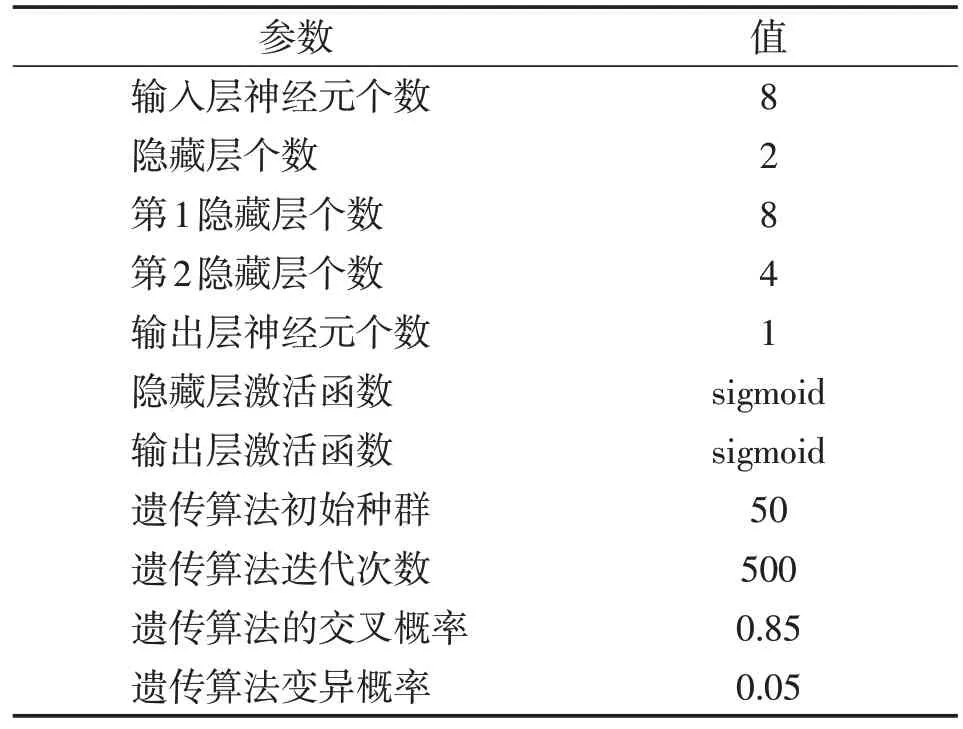
表2 模型参数

2.4 预测模型建立

采用2.2 小节中的参数，建立碳酸盐钻井的钻速GA-BPANN智能预测模型，其实现流程图如图3所示，同时建立相应的支持向量回归（SVM）和BP 人工神经网络（BPANN）预测模型，用以进行性能预测比较，其中BPANN采用的模型参数和GA-BPANN一致。

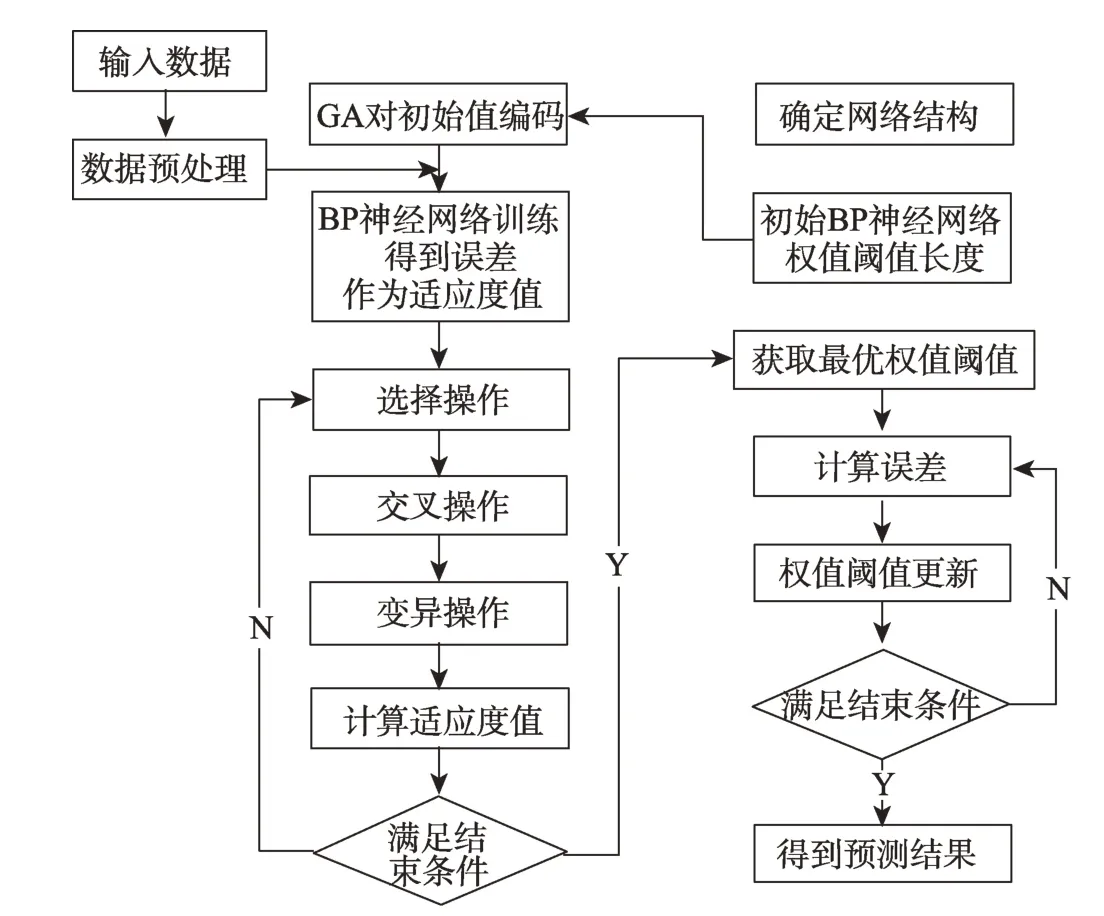
图3 GA优化BPANN流程图

2.5 模型评价

本文采用四个性能指标对所提模型的性能进行了评估。这些度量是产生的模型和实验结果之间的确定系数（R2）、平均绝对误差（MAE）、均方值误差（RMSE）和平均绝对百分误差（MAPE），分别如式（5）至式（8）所示：

式中：——预测值；

Yi——实测值；

——实测值均值。

3 预测结果及单因素分析

3.1 预测结果分析

通过上节的模型建立流程，首先进行数据预处理，然后对数据进行归一化处理，建立3个预测模型，最后对3个模型进行模型评价。三种模型模型的评价指标如表3所示。

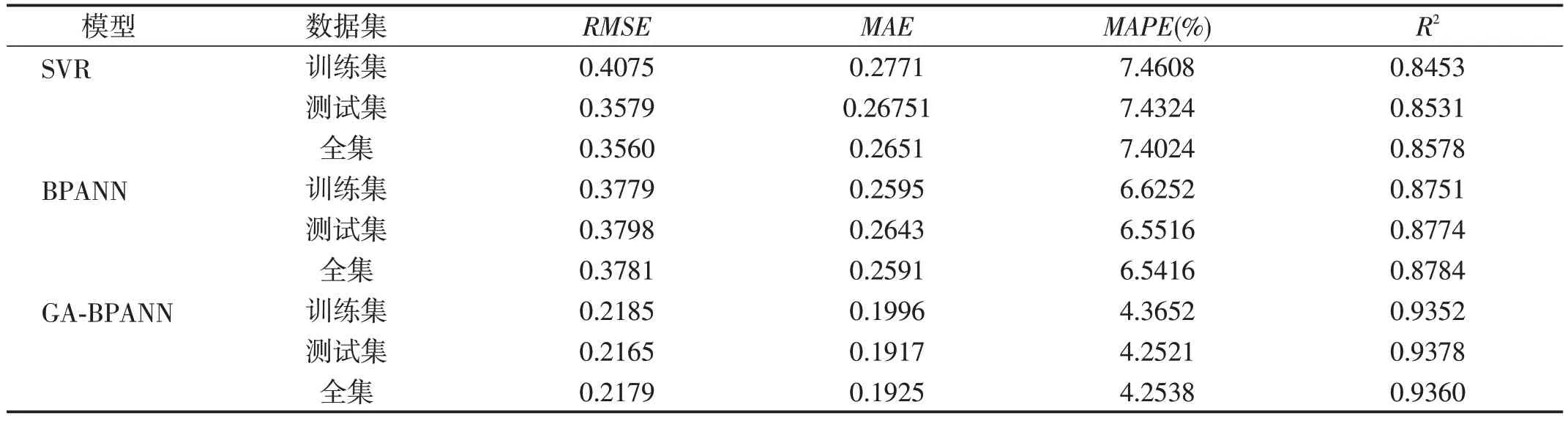
表3 模型的评价指标

为了挑选出更为精确的智能预测模型，除计算了全集R2评价指标外，还计算了RMSE、MAE和MAPE评价指标。一般认为MAPE＜10%表明预测精度较高。由表3 可知，上述预测方法的MAPE值均小于10%，说明所建立的三种智能预测模型具有较高的预测精度，其中GA-BPANN 模型的MAPE仅为4.2538%，均低于SVR 和BPANN 模型的7.4024%和6.5416%。在RMSE和MAE方面，也可以看出GA-BPANN模型的RMSE和MAE值均低于SVR 和BPANN 模型，说明采用遗传算法优化BPANN可以进一步提升模型精测精度。

为了更直观地反映本文建立的GA-ANN模型的计算误差，将全集的预测结果与实测数据进行对比，如图4所示。由图4对比可见，GA-BPANN模型的预测值与实测值分布具有较好的一致性，说明本文所建立的碳酸盐岩钻井的GA-BPANN 钻速预测模型的预测值和实测值吻合较好，可以达到准确预测的效果。

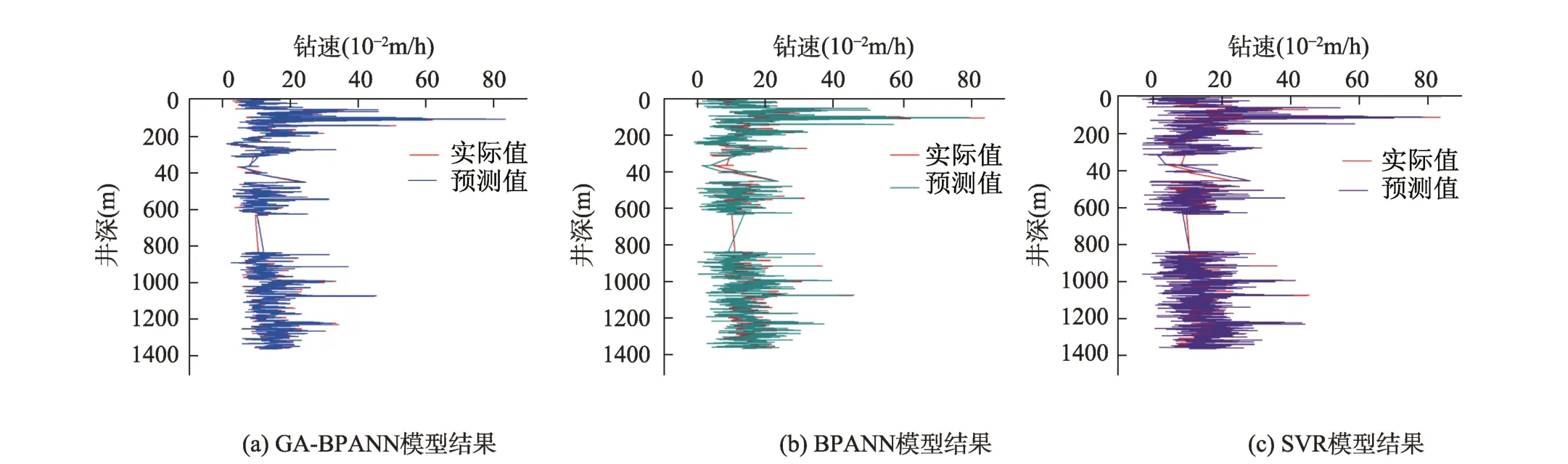
图4 模型预测结果

3.2 单因素分析

从图5（a）展示了ROP 随H 的变化规律，当深度变化时ROP 处于一个相对稳定的状态，说明钻进过程处于一种良好的状态。但是，当井深在100m 处时，ROP出现了一些较大值，可能是因为该处出现了部分软弱层造成的。从图5（b）展示了ROP随HL的变化规律,可以看出随着HL的增大，ROP具有增大的趋势，当HL在75~100kN 时得到了较高的ROP。从图5（c）展示了ROP随WOB的变化规律，当WOB小于40kN时ROP随WOB的增加具有增大的趋势，之后呈现下降趋势。从图5（d）可以看出，Q 为20 时具有较好的ROP。从图5（e）可以看出，随着RPM 的增大，ROP 具有增大的趋势。从图5（f）可以看出，随着T的增大，ROP具有减小的趋势，因为T越大需要克服的阻力越大。

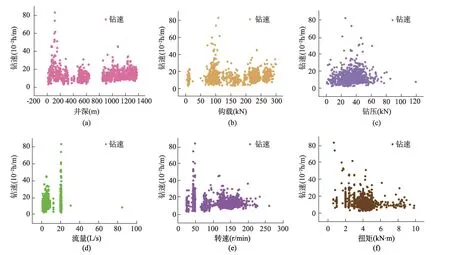
图5 不同因素对机械钻速的影响规律

4 结论

钻井钻进过程中存在的众多不确定性、时变时滞及变量间强耦合等特性，在传统理论分析中，建立多影响因素的统一数学预测模型具有很大难度，并且预测精准度较低。本文开发了基于遗传算法优化BP 人工神经网络的机械钻速预测模型。通过最大信息系数方法筛选出井深、钩载、钻压、流量、转速和扭矩作为输入变量，建立机械钻速预测模型。该GA-BPANN 预测模型具有较高的预测精度，可为后续工程应用提供技术指导。在后续研究中，收集更多的数据，建立鲁棒性更强、适用范围更广、精准度更高的机械钻速预测模型是值的研究的问题。