基于因子分析法的“双一流”建设高校生源质量评价模型研究与应用

2024-02-26张懿鑫王克勤龚思怡

创新创业理论研究与实践 2024年1期

张懿鑫，王克勤，龚思怡

（西北工业大学教务处，陕西西安 710072）

党的二十大报告提出要“全面提高人才自主培养质量”，高校人才培养的开端在招生，优质的生源质量是提高人才培养质量的首要要素。因此，要进一步提升人才培养质量，需首先提高生源质量[1]。

目前，对于生源质量的评价尚未达成共识，高校一般用入学考试成绩进行单一衡量，无法全面描绘出生源质量的精准画像，更难以提出生源质量提升的有效对策[2-6]。针对上述不足，本文重点研究以“双一流”建设高校为代表的高水平大学生源质量，通过因子分析法建立生源质量评价模型。

1 生源质量的评价模型

1.1 生源质量评价指标的确立

基于因子分析法的“双一流”建设高校生源质量评价研究的流程如图1 所示，影响指标的选取遵循全面性、客观性、相关性、可比性、明晰性、常用性原则[7]，选取录取数、计划执行率、标准化最低分、标准化平均分、标准化最高分（标准化成绩根据高考满分进行折算）、录取最低位次比、录取平均位次比、录取最高位次比（录取位次比通过该省高考人数和录取分对应位次的比值计算）、低重差（录取最低分和该省重点线的分差）、平重差（录取平均分和该省重点线的分差）、高重差（录取最高分和该省重点线的分差）、第一志愿满足率、志愿率、报到率、党团员比例、应届率、语文成绩、数学成绩、外语成绩、综合成绩进行测试，经过KMO 和Barlett 球度检验、判断后，确定本模型的影响指标分别为标准化最低分、标准化平均分、标准化最高分、平重差、录取平均位次比、志愿率、语文成绩、数学成绩、外语成绩、综合成绩，共10 个。

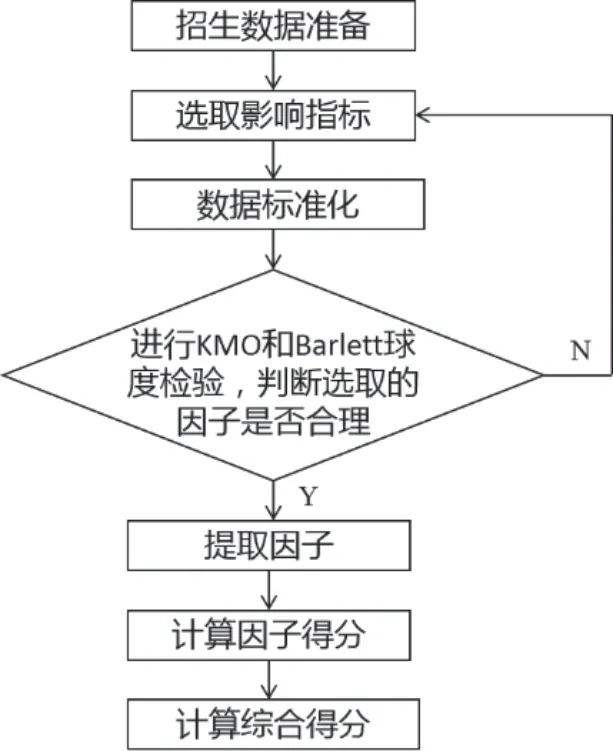
图1 研究流程

1.2 KMO 和Barlett 球度检验

研究模型以“双一流”建设高校X 为例，选取2022 年招生录取数据为研究对象，特殊类型招生（高水平运动队、高校专项计划、国家专项计划、艺术类等）因有关政策原因不具有普适性，不作为数据源进行统计。将考生原始数据进行标准化处理，采用SPSS 26.0 软件对标准化处理后的指标进行KMO 和Barlett 球度检验，计算结果如下：KMO 值为0.694（KMO 值越高，则变量间的共同因子越多，越适用于因子分析法），Barlett 球度检验统计量的观测值为261.003，自由度为45，检验的显著性概率P为0.000（P小于0.05 时，拒绝统计量相关矩阵为单位矩阵的假设，适用于因子分析法[8]）,因此，该模型适合采用因子分析法进行研究。

1.3 相关系数矩阵分析

相关系数矩阵表征指标间的关联度，系数越大，指标间代表的信息重叠度越高[9]。标准最低分、标准平均分和标准最高分3 个标准成绩间的关联程度均高于0.95，表明这3 个指标之间具有较高的关联度；标准成绩与单科成绩对比发现，3 个标准成绩与外语成绩和综合成绩间的关联程度明显高于语文成绩和数学成绩，此外，其他各项指标间也都存在一定的相关程度，因此，需采用因子分析法减小指标间的重叠信息，进一步探究生源质量的评价因素。

1.4 公因子提取

用因子分析法首先需确定因子个数，对标准化后的变量进行降维[10]，计算出所有变量相关系数矩阵的初始特征值、方差贡献率和累积方差贡献率，如表1 所示。为了不使信息丢失过多，取特征值大于0.6 的主成分作为初始因子，放弃特征值小于0.6 的主成分，即要求所得到的因子至少能解释一个变量60%的方差[11]。根据计算结果，按照特征值大于0.6 的原则提取4 个公因子，其特征值分别为5.011、2.303、1.111、0.786，累计贡献率达到92.104%，表明这4 个公因子所揭示的方差占整个方差的92.104%，因此，上述的10 个生源质量评价指标可综合成4 个公因子记为f1、f2、f3、f4,通过公因子提取一方面可以减少影响因素数量，另一方面在尽量减少信息丢失的情况下全面反映原始数据的信息。

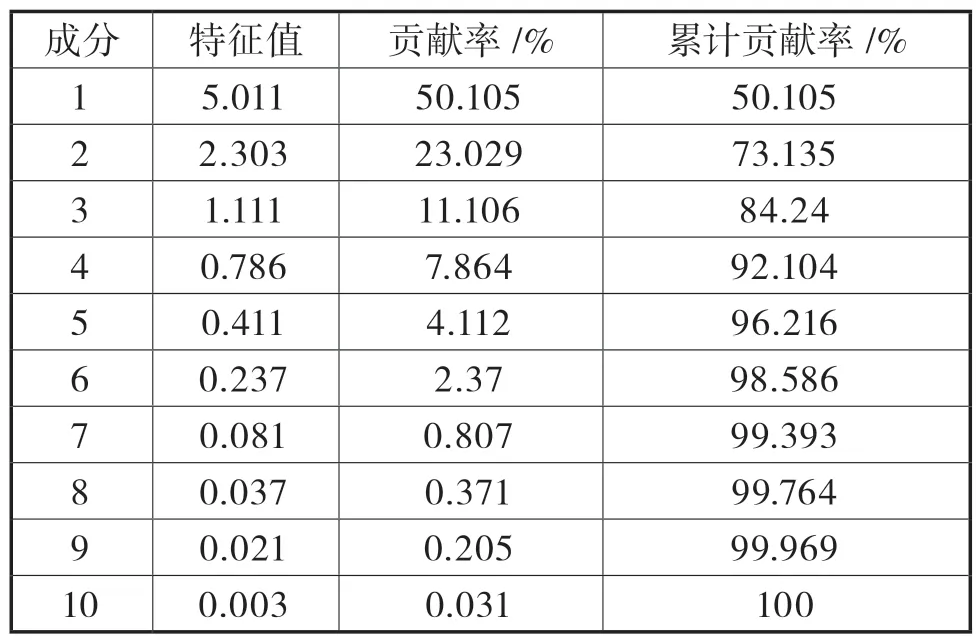
表1 生源质量评价指标相关系数的特征值及贡献率

根据因子分析原理，公因子间具备不相关性，每个因子与其所包含的指标之间具有高度相关性[9]，表2 为公因子和指标间的载荷矩阵，为进一步简化矩阵结构，将公因子载荷矩阵进行方差最大正交旋转，得到旋转后的公因子载荷矩阵，分析可知：公因子f1中，标准最低分、标准平均分和标准最高分的载荷较大，表明该公因子主要从录取分数上反映生源质量，因此命名为“分数因子”；公因子f2中，平重差和语文成绩的载荷比较大，该公因子主要从分数和重点线的差值来反映生源质量，因此命名为“分差因子”；公因子f3中，平均位次比的载荷较大，该公因子表现在位次的分布位置，因此命名为“位次因子”；公因子f4中，志愿率的载荷最大，表明该公因子主要从志愿满足情况反映生源质量，因此命名为“志愿因子”。

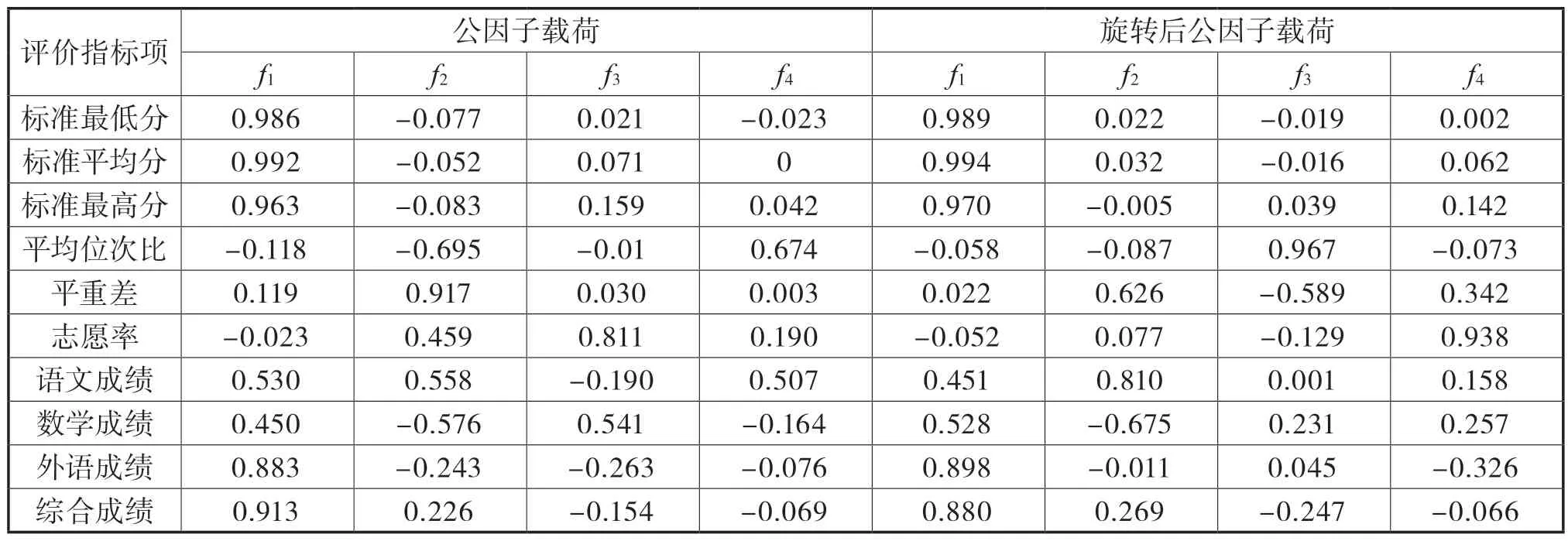
表2 生源质量评价指标公因子载荷矩阵

1.5 综合得分计算及分析

4 个因子按照公因子方差贡献率赋权求和计算综合得分，公式为：N=5.011f1+2.303f2+1.111f3+0.786f4。对4 个公因子计算其得分，并按照公式计算综合得分排序。

就综合得分而言，X 高校在天津、河南、广东、福建、广西等地生源质量较高，综合得分最高的为天津8.357 分，最低的为宁夏-12.927 分，综合得分的标准差为5.55，表明各地区生源质量分布不均。

就分数因子f1而言，天津（1.917）、四川（1.120）、北京（0.979）、云南（0.860）和河南（0.641）排在前5名，表明录取的该几个省市考生在高考成绩上表现较为突出，而内蒙古、黑龙江、甘肃、宁夏和青海则排在分数因子f1的末位，表明分数因子f1可以有效地评价录取考生的成绩水平。

排在分差因子f2前5 名的省份为广东（1.954）、福建（1.801）、湖南（1.436）、湖北1.169 和青海（0.855），该5 个省份在平重差中也排在前列，分差因子f2主要评价录取学生和该省重点线间的关系。

排在位次因子f3前5 名的省份（地区）为河南（2.282）、广西（2.090）、贵州（1.310）、云南（0.797）和甘肃（0.542），主要用于评价考生分数在该省所有考生中的分布位置。

排在志愿因子f4前5 名的省市为青海（2.110）、天津（1.325）、陕西（1.297）、甘肃（1.216）和北京（1.137），主要用于评价考生报考志愿的满足情况。

2 模型的应用价值

2.1 为生源质量评价提供科学模型

根据X 高校实际录取数据，基于因子分析法建立一套完整的高水平大学生源质量评价模型，可用于高校对省份、学院、专业等不同维度的生源质量进行全面评价，其优势在于：一是重点针对高水平大学确定影响指标，消除了如录取人数、计划执行率、报到率等对高水平大学生源质量影响较小的指标；二是通过公因子提取避免了单一指标评价的不系统和不全面；三是采用主成分分析法消除了指标间的信息重合，便于直观分析原因和差距[12]。