基于LAGRANGE 方程的深水钻井隔水管–水下井口系统动力分析

马永乾，赵鹏，畅元江，王仕超，张晏铭

1. 中国石化胜利石油工程公司钻井工艺研究院，山东 东营 257000

2. 中国石油大学（华东）海洋油气装备与安全技术研究中心，山东 青岛 266580

深水钻井隔水管系统是连接钻井平台及水下井口的导管系统，是支撑海洋钻井作业的关键核心设备，也是海洋钻井作业最脆弱环节。隔水管系统作业时将受到复杂海洋环境载荷激励和平台运动激励，使得其动态响应十分复杂且有断裂、疲劳破坏等风险，严重影响钻井作业的安全性。准确预测隔水管系统的运动状态和力学特性，对于指导深水钻井隔水管设计和作业安全具有重要意义[1]。

近年来，国内外针对钻井隔水管系统动力学建模及分析方面的研究已取得了较多进展。在针对隔水管的单独建模方面，Ham 等[2]、Iwona 等[3]基于柔性多体动力学、分段法、最小势能原理等方法建立了隔水管系统的动力学空间模型，开展了动力学特性分析；Yang 等[4]提出考虑空间柔性和活动约束的隔水管几何精确梁模型，提出动态响应的求解策略并对隔水管系统开展静力分析和反冲分析；Mao 等[5]建立了硬悬挂条件下钻井隔水管的动态分析模型，结合Newmark-β方法对模型进行了有限元求解；王宴滨等[6]建立深水钻井隔水管紧急解脱后反冲响应力学模型和控制方程，研究隔水管系统反冲响应特性。在钻井隔水管系统耦合建模方面，张慎颜等[7]采用多体动力学理论建立浮式平台–张紧器–隔水管耦合动力学模型，研究了多体耦合系统中隔水管系统的响应特性；Liu 等[8]建立了包含张紧器的隔水管系统多体动力学模型，基于所开发的程序分析了深水钻井隔水管系统在不同平台运动下的静动态特性；Low 等[9]建立了浮式平台–锚泊系统–隔水管全时域耦合动力学分析模型，认为整个系统本质的两类耦合为浮式平台/锚泊系统/隔水管的耦合以及平台平均偏移、波频运动和低频运动之间的耦合；Su 等[10]建立了SBOP–隔水管–导管系统的运动方程和自由振动方程，提出一种基于剖分延拓概念的自由振动半解析方法，并分析了井口和导管的动态响应参数敏感性；廖茂林等[11]提出了管中管动力学模型，采用 ABAQUS 有限元软件，对建立的管柱动力学模型进行动态响应模拟。目前在隔水管与防喷器组的耦合动力学建模方面还未见有文献报道，传统理论建模方法往往将钻井隔水管系统作为一个单独的研究对象来进行简化建模和分析，未考虑底部大质量防喷器组的存在及其对隔水管系统的影响，将会导致动力学分析结果与实际情况存在差异；或者采用耦合建模方法将防喷器组简化为质量和管单元的组合进行有限元分析，这种做法缺少理论依据，无法确定隔水管系统动力学分析的准确度。

由于隔水管具有超大长径比的特点，将其看作柔性梁来研究，而防喷器组因其刚度大的特点常被视为刚体模型，二者组成的系统属于典型的刚柔耦合范畴，借助于刚柔耦合动力学相关理论建立耦合模型。在刚柔耦合动力学建模方面，国内外学者已做了大量研究和探索，相关理论及方法已被广泛应用于航空航天、军事武器以及机器人等领域，而在海洋工程领域鲜有文献报道。陈思佳等[12]建立带有载荷的柔性机器人刚柔耦合动力学模型，研究柔性机器人在做大范围运动时关节铰的柔性以及杆端载荷对机器人运动响应的影响。李崔春等[13]建立挠性航天器的刚柔耦合动力学模型，研究其姿态机动轨迹并对其姿态进行控制。吕涛等[14]考虑桩腿柔性对自升式海洋平台升降作业的影响，研究平台整体升降动力学。目前主流刚柔耦合动力学建模方法有3 种：第二类LAGRANGE 法、Kane 方程法及哈密顿原理[15]，皆以分析力学原理为基础，使用能量、虚功等进行建模，其中采用LAGRANGE 方法建模不需要考虑各结构间的复杂内力关系，仅需通过计算系统动能和势能即可推导动力学方程，从而使得推导过程简洁有效。

考虑深水隔水管与防喷器组的结构特点，本文提出隔水管与防喷器组刚柔耦合概念，基于刚柔耦合理论和LAGRANGE 方程建立系统刚柔耦合动力学理论模型，采用科学计算软件和Newmark-β直接积分法进行数值计算，并以南海某深水井为例对理论模型计算结果进行对比分析。

1 深水钻井隔水管系统耦合动力学建模

深水钻井作业时，钻井隔水管与水下防喷器组通过下挠性接头连接，在海洋环境载荷的作用下，隔水管与防喷器组将发生相对运动并产生相对角位移。防喷器组坐在高压井口上并与其锁紧，受钻井隔水管柱所传递的动载荷作用，防喷器组会在水平方向产生一定往复运动。深水钻井隔水管–防喷器组运动如图1 所示。

图1 深水钻井隔水管–防喷器组运动示意

1.1 耦合系统动能

在对细长钻井隔水管进行建模时，可将其看作为柔性梁模型进行处理，梁模型上任一点P，在下挠性接头局部坐标系xjyj下的位置矢量可以表示为

式中：u(x,t)为点P的轴向位移变形，w(x,t)为点P的横向位移变形。

点P在全局坐标下的位置矢量可以表示为

式中：(rp)j为任一点P在局部坐标系xjyj下的位置向量；A(θb)是从防喷器组局部坐标系xbyb到惯性参考系的旋转变换矩阵；是从局部坐标系xjyj到局部坐标系xbyb的旋转变换矩阵，可分别表示为如下形式：

式中： θb为刚性防喷器组的转角，θj=θJ−θb为下挠性接头相对于坐标系xbyb的转角。下面分别对隔水管、下挠性接头和防喷器组的动能和势能进行推导。

隔水管系统在波流载荷以及平台运动的共同作用下会发生振动从而引起动能变化，将隔水管系统视为梁模型，其动能包括梁的横向和纵向位移变形引起的动能，可以表示为

式中：ρ为隔水管的材料密度，kg/m3；S为隔水管截面面积，m2。

将下挠性接头简化为线弹性扭转弹簧的形式，经分析可知，挠性接头运动轨迹是以水下井口基准面为圆心、以水下防喷器组高度为半径的圆周运动，基于线弹性扭簧的假设[16]，下挠性接头动能包括平动动能和转动动能，可表示为

式中：mJ为下挠性接头质量，kg；LJ为1/2 下挠性接头高度，m；JJ为下挠性接头的转动惯量，kg·m2；LB为水下防喷器组高度，m。

防喷器组的运动可描述为绕水下井口基准面中心点处的转动，其动能可以表示为

由于防喷器组形状复杂，为简化计算，在建模过程中将其等效为刚性管单元和质量单元的组合，其转动惯量可以表示为

式中：r为圆柱体半径，m；mB为防喷器组质量，kg。

将上述推导的隔水管、下挠性接头、防喷器组动能相加得到耦合系统的总动能：

1.2 耦合系统势能

隔水管梁模型的弯曲势能和拉压势能共同组成隔水管的变形势能：

式中：E为隔水管弹性模量，kPa；ρ为隔水管密度，kg/m3；I为截面惯性矩，m4。

下挠性接头的弯曲势能可以表示为

式中：kJ为下挠性接头转动刚度，kN·m/(°)。由于防喷器组自身刚度较大，自身产生的变形很小，故忽略其变形能变化。将上述推导的隔水管、挠性接头势能相加得到耦合系统总势能表达式：

将式(1)和下式表示为广义坐标的函数，并代入LAGRANGE 方程进行推导得到

1.3 隔水管系统耦合动力学方程推导

采用有限元法对柔性梁模型进行离散化，将柔性梁轴向位移u(x,t)和横向位移w(x,t)用形函数和位移函数描述为

其中，方程中部分参数表达式如下所示：

式中：M11、M22、M33分别为系统的转动惯量和梁的质量矩阵；M11是隔水管梁模型的弯曲和下挠性接头转动自由度的弹性变形对刚体转动惯量的贡献；M12、M13、M23为BOPs 运动、隔水管梁弯曲变形和下挠性接头转动变形之间的非线性惯性耦合，该系统的阻尼矩阵是挠性接头转动变形及其时间导数的非线性函数；K为受BOPs 运动和下挠性接头转角影响的刚度矩阵；M为隔水管系统刚度的质量矩阵。式(2)右端表示系统所受外力载荷向量。

2 隔水管系统耦合动力学模型求解

2.1 求解边界条件

为求解方程，取隔水管–防喷器组耦合系统的顶部和底部位移、弯矩等参数作为方程求解边界条件。选取上挠性接头处为作为上边界条件，在以往的研究中往往将下挠性接头当作下边界条件进行处理，忽视了防喷器组通过下挠性接头与隔水管的耦合关系，且忽略了防喷器组的运动，故本文考虑到其耦合关系和水下井口运动，将方程的下边界条件设置在水下井口模型底部。

若不计钻井平台的升沉运动，可将隔水管上边界条件设为简谐纵荡运动：

对于下边界条件，此处采用“等效桩法”，并取泥面下3 m 处固支约束[17]，于是下边界条件为

2.2 求解步骤

采用科学计算软件对隔水管与防喷器组刚柔耦合模型系统方程进行求解，模型求解采用Newmark-β直接积分法进行，具体计算步骤如下：

1） 初始状态计算：

② 计算系统质量矩阵M、阻尼矩阵C、刚度矩阵K；

③ 依据所需精度要求选择β、γ及Δt，并满足如下积分常数：

2）依据时间步长进行迭代计算：

① 有效刚度矩阵计算

②t+Δt时刻有效载荷计算

③t+Δt时刻位移计算

④t+Δt时刻加速度和速度计算

⑤ 重复运行步骤2）进行迭代运算。由于刚度矩阵会随时间发生变化，故每进行一个时间步的计算都需要计算新的有效刚度矩阵。为了获得稳态的刚柔耦合系统动态响应结果并可以研究更多耦合系统动态响应规律，选择1 500 s 作为分析时间。

隔水管–防喷器组–水下井口耦合动力学算法与流程如图2 所示。

图2 隔水管系统耦合动力学算法与流程

3 算例

3.1 算例参数

本文以南海某水深627 m 井为研究对象，隔水管系统配置见表1，隔水管外径0.533 4 m，壁厚0.015 875 m；导管外径0.762 m，壁厚0.025 4 m。海水密度和钻井液密度分别为1 025 和1 200 kg/m3。通过底部残余张力法[18]确定隔水管顶部张紧力为2.01 MN。上、下挠性接头转角刚度分别为733.386和1 873.572 KN·m/(°)，LMRP/BOPs 参数来自某深水钻井平台。海流剖面见表2，波高取8.4 m，波浪周期为12.1 s。

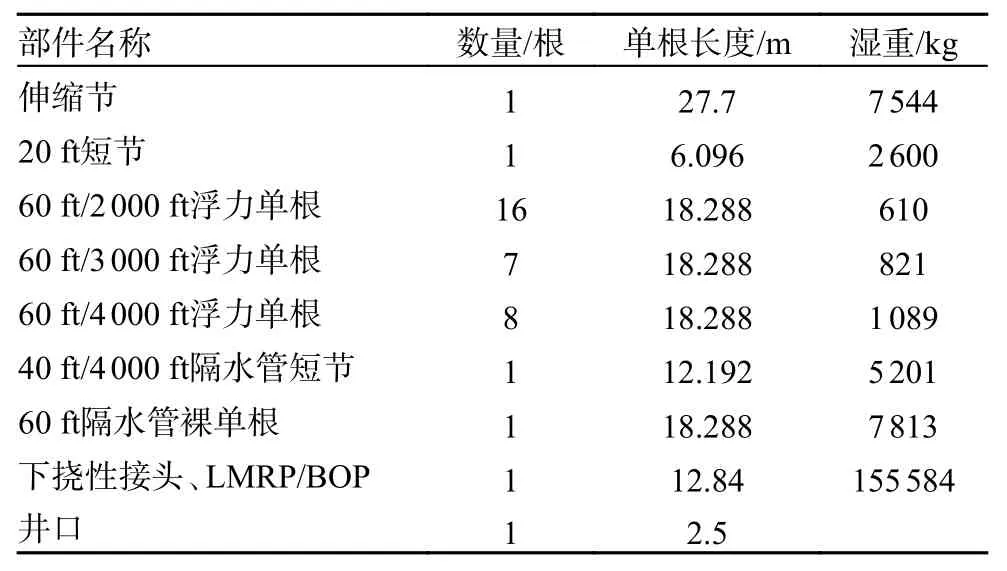
表1 钻井隔水管系统配置

表2 钻井隔水管系统配置

3.2 动力学分析与模型验证

本节借助有限元分析软件ABAQUS 建立隔水管–防喷器组刚柔耦合动力学仿真模型，根据挪威船级社的推荐做法建立水下井口等效模型，具体建模及等效过程见文献[17]。以上述627 m 水深隔水管系统为例，建立隔水管–防喷器组–水下井口系统耦合动力学理论模型和ABAQUS 仿真模型进行动态响应对比分析。根据文献[17]的方法，采用ABAQUS 建立隔水管系统有限元模型时，将隔水管采用管单元进行模拟，防喷器组被建模为管单元和质量单元的组合，管外径为0.914 4 m，壁厚为0.219 m，质量根据LMRP/BOPs 的实际质量沿高度方向平均分配。提取500 s 隔水管系统不同位置处节点位移、单元弯矩以及上、下挠性接头转角等时间历程，分别如图3～5 所示。图3～5 中红色实线为本文理论模型的计算结果，蓝色虚线为ABAQUS 仿真模型计算结果。

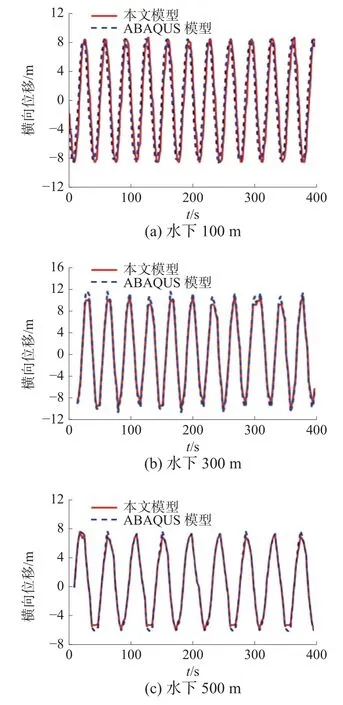
图3 隔水管系统横向位移时程曲线

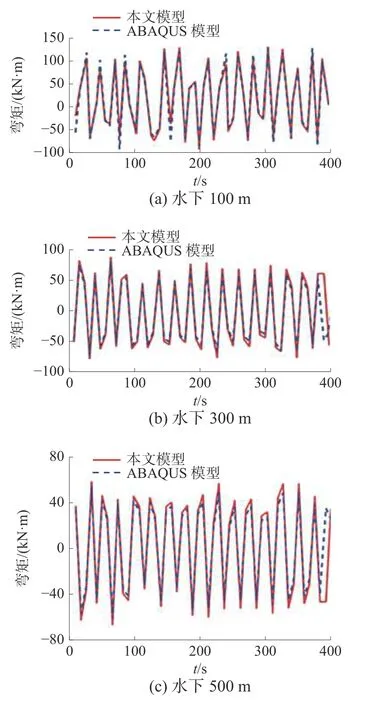
图4 隔水管弯矩时程曲线

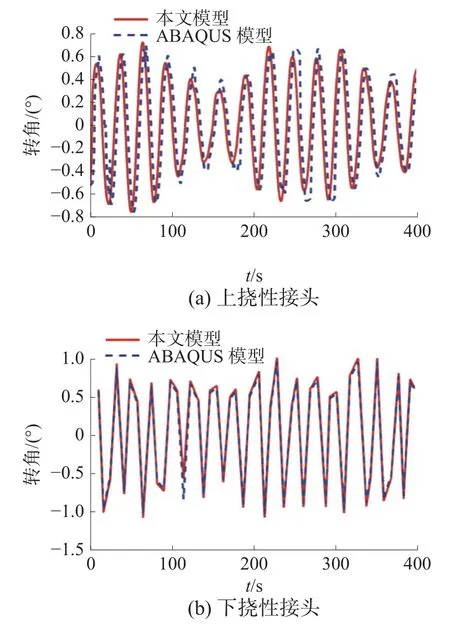
图5 上、下部挠性接头转角时程曲线

由图3～5 可知，采用本文建立的隔水管–防喷器组刚柔耦合动力学模型得到的动态响应计算结果，包括位移、弯矩和转角等时程曲线，均与ABAQUS 仿真结果吻合良好。2 种模型动态响应幅值均值最大偏差为8.8%，初步证明了本文理论模型的正确性。

为了进一步验证本文模型的计算精度，此处提取隔水管横向位移包络线和弯矩包络线进行对比验证，分别如图6 和图7 所示。图6～7 中，实线为本文理论模型计算结果，虚线为采用文献[17]方法的计算结果。

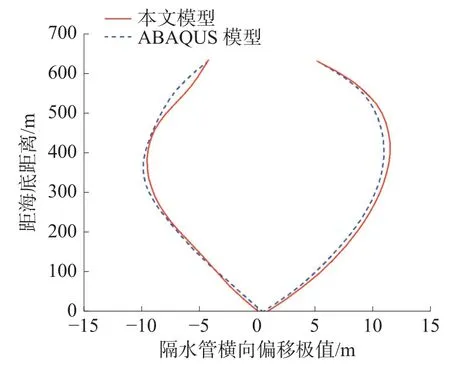
图6 整体侧向位移包络线结果对比

图7 整体弯矩包络线结果对比

由图6 和图7 可知，采用本文理论模型和参考文献模型得到的隔水管整体横向变形包络线、整体弯矩包络线计算结果吻合良好，2 种模型得到的隔水管整体横向变形包络线范围分别为−9.9～11.4 m 和−9.93～10.95 m；得到的隔水管整体弯矩包络线范围分别为−113.97～128.47 kN·m 和−115.65～124.93 kN·m。由此可见，相较于ABAQUS仿真模型，本文根据柔性隔水管与刚性防喷器组的结构特点所建立的隔水管–防喷器组–水下井口系统耦合动力学模型更接近于实际情况，更加适用工程应用环境，在隔水管系统耦合动力学分析上具有专用性。在计算效率上，本文模型计算效率高、求解速度快且计算结果更加准确。

4 结论

本文开展基于LAGRANGE 方法的深水钻井隔水管–防喷器组–水下井口耦合系统动力学建模与数值计算研究，所取得主要结论如下：

1）基于刚柔耦合动力学理论，采用LAGRANGE方法和有限元法建立隔水管–防喷器组–水下井口系统耦合动力学理论模型，采用Newmark-β直接积分法对动力学模型进行求解并采用科学计算软件开发动力学求解程序，实现了基于LAGRANGE方法的隔水管–防喷器组–水下井口系统耦合动力学数值计算。

2）以南海深水隔水管为算例开展动态响应分析，采用ABAQUS 建立隔水管–防喷器组–水下井口系统仿真模型，计算得到理论模型与仿真模型在节点横向位移、单元弯矩及上部和下部挠性接头转角等吻合良好，动态响应幅值均值偏差为8.8%。

3）对理论模型和ABAQUS 有限元仿真分析得到的整体侧向位移包络线和弯矩包络线进行对比分析，结果表明2 组包络线亦吻合良好，证明采用本文理论模型进行仿真分析时可以将防喷器组模拟为刚性管单元和质量单元的组合，从而可为深水隔水管和水下井口系统动态分析提供理论参考。