直流支撑电容器圆元件的散热模型与仿真研究

2024-02-25左强林雷乔舒钟少龙张涌新党智敏

电力电容器与无功补偿 2024年1期

左强林，雷乔舒，钟少龙，张涌新，党智敏

（1.无锡赛晶电力电容器有限公司，江苏无锡 214177；2.清华大学电机系新型电力系统运行与控制全国重点实验室，北京 100084）

0 引言

自愈干式金属化薄膜电容器因储能密度高、体积小、对环境友好而得到广大用户的青睐，在电动汽车、电力机车、脉冲功率等领域得到快速的应用和发展［1-8］。我国柔性直流输电技术的发展，为可应用于柔直工程的自愈干式直流支撑电容器带来了新的契机，各大院校、各个电容器厂家和相关机构对于柔直用直流支撑电容器的研究如火如荼［9-11］，相关技术问题也得到了分析与探讨，如直流叠加交流下的自愈性能问题［12］，温升分布不均匀问题［13］等。

柔直用直流支撑电容器与传统的高压油浸式电容器有很大的区别，电容器内部的散热方式只有热传导散热，且柔直用直流支撑电容器的容量大，损耗高，电容器的内部温升情况以及变化规律是众多高校、制造厂家研究的关键技术问题［14-16］。

柔直用直流支撑电容器在户内柔直环流塔中使用，而柔直换流塔的空间有限，导致柔直用直流支撑电容器的温升问题更为突出，用户对柔直用电容器内部温升也极为关注，这也造成了对电容器进行热仿真的需求。热仿真的前提是建模，建模的前提是对电容器的内部结构和性能特别是元件有充分的了解。陈红晓等对金属化膜脉冲电容器放电过程进行了热仿真与分析［17］，但未针对内部元件进行详细建模分析；李化等对高压交流金属化膜电容器的温升特性进行了建模仿真和试验验证［18-19］，但交流和直流电场下的热传导性能大有不同，且运行工况也完全不一样。随着计算机技术和算法的快速发展，有限元方法在解决多物理场耦合问题中表现出明显的优势[20]，而多物理场耦合环境更加符合元件工作的实际状态。郭小凡等人[21]通过电-热耦合得到了金属化膜电容器在多电平换流器工况下的温升特性，为设备的设计提供了有力的数值支撑。Yao 等人[22]建立了聚丙烯薄膜电容热-化学腐蚀多场有限元模型，对不同工况下电容器寿命进行了预测分析。Huang 等人[23]通过热-力耦合分析了多层陶瓷电容器的热应力分布。

目前国际上柔直用直流支撑电容器有两个技术方向，一个是扁元件，一个是圆元件。扁元件的热传导计算与传统的高压油浸式电容器类似，但和圆元件不太一样。本文研究对象是圆元件，研究问题包括圆元件的发热特性和热阻计算推导等。由于元件内部的温度目前没办法进行实测［24］，因此本文通过推导计算，得到圆元件的散热规律，通过试验验证，提出元件内部最热点温度的估算方法。最后采用电-热多物理场耦合有限元方法分析了损耗引起元件温度升高的分布情况，为研究柔性直流支撑式电容器整体发热分析奠定基础。

1 圆元件的散热问题研究

圆元件的散热问题比较复杂，首先元件本身整体是发热体，发热主要来自金属镀层和薄膜介质极化［25］，其次元件内部的热流密度是变化的，目前暂未有精确的计算公式。圆元件的散热由2 部分组成，1）轴向散热，2）径向散热［26］，下面做具体分析。

1.1 轴向散热

圆元件发热量分布在元件的有效部分，考虑到膜的发热是均匀的，可以认为发热量与发热体的体积成正比。对于从元件中线零点0 到元件端面Ly/2 之间任意处z，圆元件的轴向散热示意图见图1。

根据热工学原理［22］和热电对偶原理［22］，dz 处的热阻dRz为

式中：D为元件直径，m；d为心棒直径，m；λz为元件轴向导热系数，W/m·K。

0 到z 处的发热量（也就是流经dz 的热流）为

dz 处的温升dθz应为dRzPz，在0-Ly/2 内对dθz进行积分并化简，可以得到

式中：P为元件发热量，W；Ly为元件长度，m。

考虑到金属电极厚度很小且心棒和元件内外径比很小，则在工程上圆元件的截面积与金属化膜的长度与厚度的乘积可以被认为是一样的，即另外根据导热系数的定义，金属化膜宽度方向的导热系数由聚丙烯薄膜和镀层两部分合成。考虑到元件有两个端面，两个端面到元件中心线的热阻是并联关系。式（4）可以改写成

式中：λm、λjb分别为聚丙烯和镀层的导热系数，W/（m·K）；dm、djb分别为聚丙烯薄膜和镀层的厚度，m；Lm为金属化聚丙烯薄膜的有效长度，m。

如果按照热阻的定义，元件中心线到端面的热阻应为

对比式（7）与式（4）~（6）可以看出，按照元件分散性发热模型得到的热阻，只有直接按热阻定义得到的热阻的1/4，说明整体发热的热阻，不能按热阻定义来直接计算。

1.2 径向散热

对于圆元件，参考电缆的电阻计算模型，先假定元件的长度远大于直径。圆元件的径向散热见图2。

图2 圆元件径向散热示意Fig.2 Radial heat dissipation schematic diagram of circular element

圆元件发热量分布在元件的有效部分，考虑到膜的发热是均匀的，可以认为发热量与发热体的体积成正比。对于从心棒r到元件外径R之间任意处x，由热工学原理［22］和电热对偶原理［22］，dx处的热阻为

式中：Ryx为元件径向等效热阻，K/W；λx为元件径向导热系数，W/m·K。

r到x处的发热量（也就是流经dx的热流）为

dx处的温升dθx应为dRxPyx，在r-R内对dθx进行积分并化简，可以得到

式中，ΔTyx为元件径向温升，K。

元件径向热阻就是金属化膜的厚度方向热阻，由聚丙烯薄膜的热阻和镀层热阻串联组成。由于镀层厚度远小于薄膜的厚度，导热系数远大于薄膜的导热系数，元件的径向热阻可以看成就是聚丙烯薄膜的热阻，径向导热系数可以认为就是聚丙烯薄膜的导热系数，即λx≈λm。这样式（11）可以写成：

实际上轴向和径向的散热是同时进行的，根据热电对偶原理［22］，元件的热流按热阻的反比例分配。计算公式为

基于式（3）、（10），可以计算得到圆元件的散热及温升与元件尺寸的关系见图3-4。

图3 元件直径与散热的关系Fig.3 Relationship between element diameter and heat dissipation

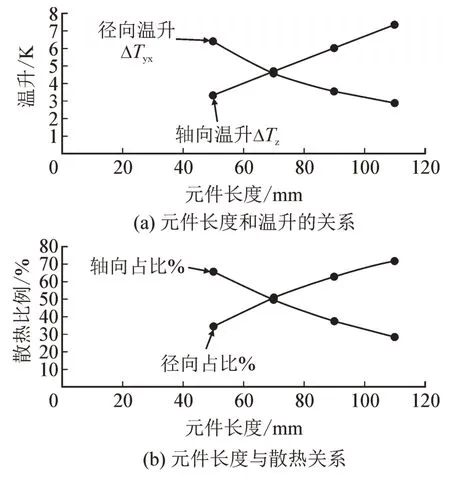
图4 元件长度与散热的关系Fig.4 Relationship between element length and heat dissipation

从图3-4 可以看出，元件的散热与元件的直径和长度有关，具体散热情况需要根据尺寸设计的具体情况确定。一般来说，元件的长径比越大，径向散热比例越大。

2 圆元件轴向散热和径向散热试验验证

2.1 元件散热模型

要对圆元件的散热进行验证，首先要建立圆元件的散热模型。根据前面的推导，圆元件的散热由径向散热和轴向散热2 部分组成，且为并联的形式。元件的热阻为

设介质的能量密度为A0，则有：

这样元件的温升为ΔTy=RyPy。将式（14）-（15）代入并化简得

为考虑理论计算与验证结果的等效性，等式右边考虑一个系数k0，这样式（16）、（17）可改写为：

式中A0与元件设计的损耗参数有关，可以通过试验确定。其余同上。

从式（16）可以看出，元件的长度越大，温升越高，元件的直径越大，温升也越高。具体见图5。

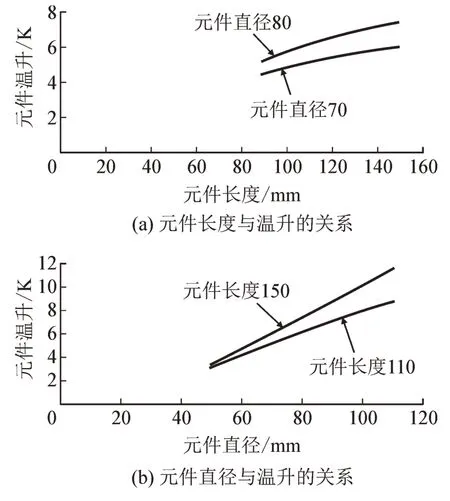
图5 元件尺寸与温升的关系Fig.5 Relationship between element size and heat dissipation

考虑到元件本身是均匀发热体，元件中单位体积的发热量与εE2/2 成正比，考虑到元件损耗为tanδ，式（16）可以改写为

从式（20）可以看出，圆元件的温升与元件的设计场强的平方成正比。对于金属化膜元件，由于非金属镀层的留边和空白边宽度通常小于5 mm，没有镀层的薄膜表面积占比很小，金属化膜发热体积与元件本身的体积可视为基本相等，β可以视为1，元件温升试验表明，系数β为1.02 以内，工程计算可以取β=1。

2.2 验证方案简介

下面为验证元件散热模型，选取元件尺寸为Ф77×103 的试品元件做对比试验。元件参数见表1。

表1 试品元件的基本情况Table 1 Basic situation of sample element

试验验证包括3 个方面：圆元件温升、圆元件径向和轴向散热比例以及式（19）的系数A1、k0的确定。为此，试品元件做如下处理：

1）4 个元件不做绝热处理，元件编号为1-1#-1-4#。见图6。

图6 正常试品元件Fig.6 Normal sample element

2）2 个元件在元件径向做绝热处理，元件编号1-5#-1-6#，见图7（右边的两个元件，只有轴向散热）。

图7 做绝热处理的元件Fig.7 Element for adiabatic treatment

3）2 个元件在元件的两个端面（轴向）做绝热处理，元件编号1-7#-1-8#，见图7（左边的2 个元件，只有径向中间部位散热）。

2.3 验证结果分析

2.3.1 试验验证结果

在环境温度为65℃的条件下，对元件施加510 V工频交流电压进行温升试验，温升试验的稳定条件按照标准规定，在6 h 内温度变化不超过1 K。最终试验结果见表2。

表2 元件温升试验结果（环境温度65 ℃）Table 2 Temperature rise test results of element（Ambient temperature at 65 ℃）

2.3.2 数据分析

从表2 可以看出，利用电缆+分布式发热模型计算圆元件的温升是在工程上可行的，但需要考虑一个修正系数k0。由于径向绝热很难做到完全的绝热，试验温升结果与计算结果偏差略大。

经过绝热处理的元件温升试验结果表明，圆元件的径向散热和轴向散热的计算推导基本正确，可以用于指导工程设计。对于验证试品，径向散热占62.4%，轴向散热占37.6%，与元件的长径比有关。需要注意的是，元件的散热模型与电容器的散热模型不是等同的，随着元件放置方式不同，散热模型也不一样。

2.3.3 电-热多场耦合有限元仿真分析

进一步采用有限方法对元件温升试验进行了数值计算，构建了电-热多物理场耦合仿真模型，在电流场中计算出不同试验条件下元件内部的损耗大小，传入固体传热场中作为热源引起元件温度升高。元件表面通过对流方式向空气散热，环境温度为65 ℃，而在径向和轴向绝热仿真中，对应表面设置为绝热边界条件。则在无绝热、径向绝热和轴向绝热3 种条件下，元件的温度分布见图8。

图8 不同条件下元件温度分布云图Fig.8 Temperature distribution cloud diagram of element under different conditions

由图8 可知，对于无绝热、径向绝热和轴向绝热3 种条件下，元件温度范围分别为68.7~70.4℃、73.4~75.3 ℃和71.6~74.4 ℃，与表2 试验测量结果吻合，径向绝热条件下元件温度大于轴向绝热条件。此外，在无绝缘状态下（图8（a），元件内部温度并非均匀分布，而随空间位置的变化而改变，从心棒到外表面，元件温度先增大后降低，最高温度点分布约在径向1/3 的位置。