基于多分辨率-多边形单元建模策略的多材料结构动刚度拓扑优化方法
2024-02-25江旭东马佳琪滕晓艳王亚萍
江旭东,马佳琪,熊 志,滕晓艳,王亚萍
(1.哈尔滨理工大学机械动力工程学院,哈尔滨 150080;2.哈尔滨工程大学机电工程学院,哈尔滨 150001)
在飞机、汽车制造与结构工程领域,多材料设计兼顾每一相基材料的有点,能够保证结构具有综合的力学性能,因而在飞机、汽车与桥梁结构中的应用日益增多[1-3]。拓扑优化方法能够寻求满足性能约束条件下材料的最优布局,极大地丰富了多材料结构的设计手段。与传统单一材料的拓扑优化相比,多相材料的拓扑优化极大地扩大了设计空间,能够提供综合性能更优的最优解。随着多材料增材制造技术的发展,依据最优拓扑的计算模型,使通过逐点和逐层方式打印多材料设计结构成为可能[4-6]。由此,多材料的拓扑优化问题引起了研究机构的广泛关注。根据设计变量的定义方式,多材料拓扑优化方法通常归纳为2 类:基于单元的方法[7-18]和基于边界的方法[19-23]。在基于单元的方法框架内,ZUO 等[7]、杜义贤等[8]、闫浩和吴晓明[9]通过构造材料性能的序列插值模型,实现了柔性机构和传热机构的多材料最优布局设计。俞燎宏等[10]和朱本亮等[11]采用交替主动相算法,将多相优化布局问题转变为序列两相材料优化子问题,然后通过并行计算策略逐级分层计算。目前,多体积约束下的多材料布局优化已拓展至稳态热传导[12]、热力耦合[13-14]、频域动力学[15]和空间桁架结构[16]的最优布局问题。最近,YANG和LI[17]、HUANG 和LI[18]则提出了单一质量约束下的多材料轻量化设计方法。在基于边界方法的框架内,水平集法[19-21]和移动构件法(MMC)[22-23]因其能使边界光滑清晰、便于提取设计构型等独特优势,也受到了一定的关注与研究。但是,现有的基于边界的方法未能充分考虑新孔洞的创建,优化结果过度依赖于初始设计,难于获得优化问题的全局最优解。
拓扑优化框架要求在消耗尽可能小的计算成本下获得高分辨率的优化结果,而上述目标的实现取决于有限元求解器、自由度数量、优化建模策略、材料插值模型以及后处理等诸多因素。SUKUMAR[24]首次提出了多边形有限元法,数值实验表明它非常适于求解具有复杂几何结构区域的连续介质力学问题。将多边形单元应用于拓扑优化问题,能够显著地减小棋盘格和孤岛效应等数值奇异性问题[25-28]。为了减少计算成本与提高求解精度,NGUYEN-XUAN[29]构建了多边形有限元法与自适应网格重划技术融合策略,CHAU 等[30]基于上述研究工作求解了多材料结构的静态拓扑优化问题。另外,NGUYEN 等[31]提出了高分辨率拓扑优化方法 (multiresolution topology optimization,MTOP),它采用多层级网格优化建模策略,即利用粗糙网格完成有限元分析,精细的重叠网格描述设计变量和密度变量空间,从而形成高分辨率的拓扑优化结果。最近,FILIPOV 等[32]将多边形单元替代传统单元作为分析单元,精确地估计复杂结构的动力学响应,高效地实现了特征值、受迫振动等结构频域动力学问题的高分辨率拓扑优化。
在结构时域动响应方面,以提高结构动刚度[27,33],降低结构振动幅度[34-35]和动应力幅值[28]等拓扑优化方法相继提出。SHOBEIRI[33]在敏度分析中忽略了动能对单元删除的影响,难于获得惯性力影响显著的动力学拓扑优化解。ZHAO 和WANG[34]、GIRALDO-LONDOÑO 等[27-28]分别采用了先微分-后离散和先离散-后微分的伴随敏度分析方法,但是,后者基于多边形单元计算结构动响应,能够处理任意曲线边界结构的动力学优化问题。针对模型减缩技术在动力学拓扑优化过程中的有效性问题,ZHAO 和WANG[35]指出模态加速法在减少响应计算规模和预测精度上的平衡能力优于模态位移法,然而,如果高频模态为主要影响模态时,模型减缩技术将失效。
多相材料时域动力学布局优化问题属于强非自伴随问题,需要考虑多材料结构的动态约束条件,致使敏度分析和优化问题求解具有挑战性,因而目前的多相材料布局优化集中于静态优化问题,而多相材料的时域动力学布局优化问题研究相对较少。因此,本文将多边形网格与MTOP 的融合方法拓展至多材料结构的动态拓扑优化问题,建立融合框架内的多相材料高分辨率布局的时域动力学优化模型。为了避免先微分-后离散方法引起的灵敏度计算的相容性误差,采用先离散-后微分的伴随敏度分析方法。通过泰勒公式实现近似描述目标函数和体积约束函数,建立原问题的凸规划子模型,采用基于敏度分离技术的ZPR方法求解子问题。最后,通过数值算例检验提出的方法在多相材料动力学布局优化的可行性。
1 多分辨率-多边形网格建模策略
多边形单元在动力学分析方面其求解精度优于传统单元,因而将其作为动力学优化问题的响应计算单元[25-28]。同时,将多边形单元劈分为精细的小单元形成设计变量与密度变量网格,并使两者具有相同的位置坐标,继而构建多分辨率-多边形单元的优化建模策略,能够实现粗糙位移网格条件下的高分辨率的拓扑优化构型设计(如图1所示)。多分辨率-多边形单元建模策略,利用粗糙的多边形网格精确求解位移场,精细的设计变量与密度变量重叠网格用于构型优化设计,将有效地提升优化计算效率与优化结果的品质[26]。
在MTOP 框架内,为了精确计算多边形位移单元的单元刚度矩阵,将形函数及其梯度的积分点设置在密度变量所在位置(也是设计变量网格的中心)。对于多材料问题,单元刚度和质量矩阵分别表示为:
式中:Nn为多边形位移单元积分点的个数;yℓ,ij为密度变量在积分点处的估计值;Bℓ为应变矩阵,D0为线弹性材料本构矩阵;Aℓ,i为设计变量网格或密度变量网格的面积; ρ0为材料密度;m˜E(yℓ,ij)和m˜V(yℓ,i j)为m种材料的刚度与体积差值函数。
基于门槛投影函数[36],体积插值函数表示为:
式中,p0>0为惩罚参数。然后,构造多材料刚度插值函数,表示为[38]:
式中,Ei为第i种材料的弹性模量。
由此,根据上述单元刚度与质量矩阵,多边形位移单元的总体矩阵表示为:
为了抑制棋盘格与孤岛现象,利用线性滤波方法获得网格无关的优化结果,则有:
式中:Si为相应于密度变量单元i所占的子域;xn为与设计变量dℓ,nj对应的设计变量网格的中心坐标。线性权重函数定义为:
式中:rni为单元密度单元i和n的中心距;rmin为指定的过滤半径。通过式(8)将设计变量线性加权处理而映射为密度变量,以此代入式(1)和式(2)中即可获得单元刚度与质量矩阵。
此外,根据式(8),密度变量对于设计变量的灵敏度为:
2 多材料结构动刚度拓扑优化
2.1 优化模型
以平均动柔度最小化为目标和多材料的体积占比为约束,建立多材料结构的动力学拓扑优化模型。假设设计域中包含m种材料,按弹性模量高低线性排列,在有限材料约束下,其动刚度优化模型为:
式中:d为设计变量矢量;Nt为动态激励作用时间定分的区间数;Nc为多材料体积约束的数量;fi为t=ti时的动载荷向量;ui、u˙i、u¨i分别为相应的结构位移、速度、加速度响应;C=αrM+βrK为阻尼矩阵( αr、 βr为瑞利阻尼参数); εj、 ηj、χj分别为单元指标集、设计变量指标集和多材料相数指标集,为第j种材料占设计域总体积的体积分数。
2.2 HHT-α 方法
HHT-α 方法作为广义的Newmark-β 方法,它通过数值阻尼参数α 调控动力学控制方程的积分格式,使迭代过程无条件稳定,非常适于求解结构动力学问题。根据文献[39],HHT-α 方法将优化模型式(11)中的半离散形式的有限元方程修改为:
通过Newmark-β 有限差分关系,位移、速度场的更新格式为:
式中,β=(1+α)2/4 ,γ= (1+2α)/2为算法参数,合理选择参数α 保证算法具有至少二阶精度和无条件稳定。
将式(13)、式(14)代入式(12),得到离散形式的控制方程的残差,则有:
对于HHT-α 残差方程式(15),其初始时刻的表达式为:
2.3 敏度分析
根据优化模型式(11),在MTOP 框架内目标函数对于设计变量的灵敏度为:
为了避免状态变量对于设计变量的导数计算,使用伴随变量法完成目标函数的敏度分析。类似于HHT-α 残差方程式(15),将Newmark-β 有限差分关系式(13)、式(14)变换为残差形式:
根据式(19)、式(20),∂Pi/∂dℓ,n j=0 和∂Qi/∂dℓ,nj=0以及初始条件∂u0/∂dℓ,nj=0 和∂u˙0/∂dℓ,nj=0,同时,满足伴随方程式(23)和式(24)使∂u¨0/∂dℓ,nj、∂u¨i/∂dℓ,nj、∂u˙i/∂dℓ,nj和∂ui/∂dℓ,n j等项消失,则式(21)化简为:
将HHT-α 残差方程式(15)、初始条件式(17)和Newmark-β 有限差分关系式(13)、式(14)代入伴随方程式(23)、式(24),则有:
由于优化模型式(11)中使用了体积插值函数V=与刚度插值函数E=,那么通过链式求导法则,拉格朗日函数与约束函数的灵敏度为:
我们这一代人一般都是三口之家。三居室的分配是这样的:夫妻一间,孩子一间,书一间。书跟人平起平坐,甚至因书太多,书房得足够宽敞,孩子只能屈尊居于小房间。
另外,根据优化模型式(11),目标函数和约束函数对于V=和E=的敏度表示为:
结合式(1)、式(2)和式(7),HHT-α 残差方程对于V=和E=的偏导数表示为:
由此,根据式(25)~式(28)确定伴随变量,随后将式(31)~式(37)代入式(29)和式(30),则可确定拉格朗日函数与约束函数的灵敏度。
2.4 ZPR 设计变量更新方案
利用凸近似方法,优化模型式(11)的近似子问题:
式(42)表明,每一个设计变量仅与一个约束函数相关,因而拉格朗日函数L可采用分离变量的方法求极值。鉴于Li的可分离特性,其一阶最优条件为:
将式(45)代入式(42),获得子问题的对偶目标函数,根据Li(d(λi),λi)的相互独立性,寻求拉格朗日乘子 λi使其达到极大值,则Li(d(λi),λi)的驻点条件表示为:
式(46)为关于 λi的非线性方程,可通过区间收缩法或迭代法求解。
3 典型算例
本节通过悬臂梁、简支梁、L 型结构与Michell型悬臂梁4 个典型数值算例,对比4 种工况:①静态载荷;② 载荷持续时间为0.05 s;③ 载荷持续时间为0.03 s;④ 2 种~10 种不同弹性模量(Ei=E0(m-i+1)/m,i=1,2,···,m,m=2,3,···,10,如图2 所示)多相材料的优化结果。分析该优化方法的可行性和动态载荷作用时间对优化结果的影响机制。

图2 多相材料的弹性模量Fig.2 Elastic modulus of multiphase materials
对于任一种多材料优化工况,每一相材料体积约束的上限v¯j=0.45/m(j=1,2,···,m)。另外,为了确保HHT-α 方法至少具有二阶精度和无条件稳定性,所用算例均使用α=0.05 ,β=(1+α)2/4,γ= (1+2α)/2。
3.1 悬臂梁
如图3 所示,悬臂梁右侧自由边中点处承受正弦半波载荷f(t)=f0sin(πt/tf),载荷幅值f0=1 kN,初始设计域的结构尺寸为L×H×h=8 m×4 m×0.01 m。多相材料的基准弹性模量E0=200 GPa,任一材料相的泊松比νi=0.3,密度ρi=7800 kg/m3,瑞利阻尼参数αr=10 ,βr=1×10-5。

图3 悬臂梁Fig.3 Cantilever beam
图4 为悬臂梁双材料设计的迭代历史(载荷作用时间tf=0.05 s)。目标函数渐进收敛于0.0294 N·m,软、硬两相材料均渐进收敛于体积约束的上限:
图5 为不同载荷持续时间工况下双材料悬臂梁问题的优化设计结果。静力学的优化拓扑更接近于动力学tf=0.05 s的结果,但是,动力学tf=0.03 s的优化拓扑显著不同于前两者的结果。与静力学解相比,动力学解分布硬的材料相或三角形结构用于强化载荷作用点处的刚度,以抵制动载荷的快速波动。如图6 所示,静力学工况的位移与动柔度响应均高于动载荷工况,从而验证了前面的假设。另外,tf=0.05 s工况下的设计将硬材料相置于载荷作用端,使其产生较小的变形,因而具有更高的动刚度。

图5 双材料悬臂梁问题动静态载荷优化结果对比Fig.5 Comparison of dynamic and static load optimization results of bimaterial cantilever beam
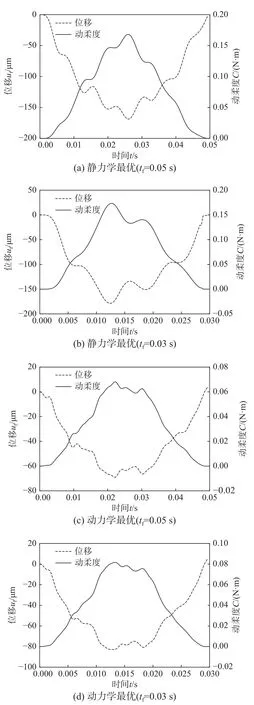
图6 最优悬臂梁载荷作用点处垂向位移和动柔度时间历程Fig.6 Time history of vertical displacement and dynamic flexibility at the loading point of optimal cantilever structure
图7 为tf=0.05 s时悬臂梁多材料拓扑优化结果。外部拓扑结构基本一致,内部拓扑结构依靠交叉肋结构强化,随着材料相数目的增加,低弹性模量材料向固定端分布,特别是对于4 种材料和10 种材料工况,固定端增加了强化结构平衡惯性力的影响。
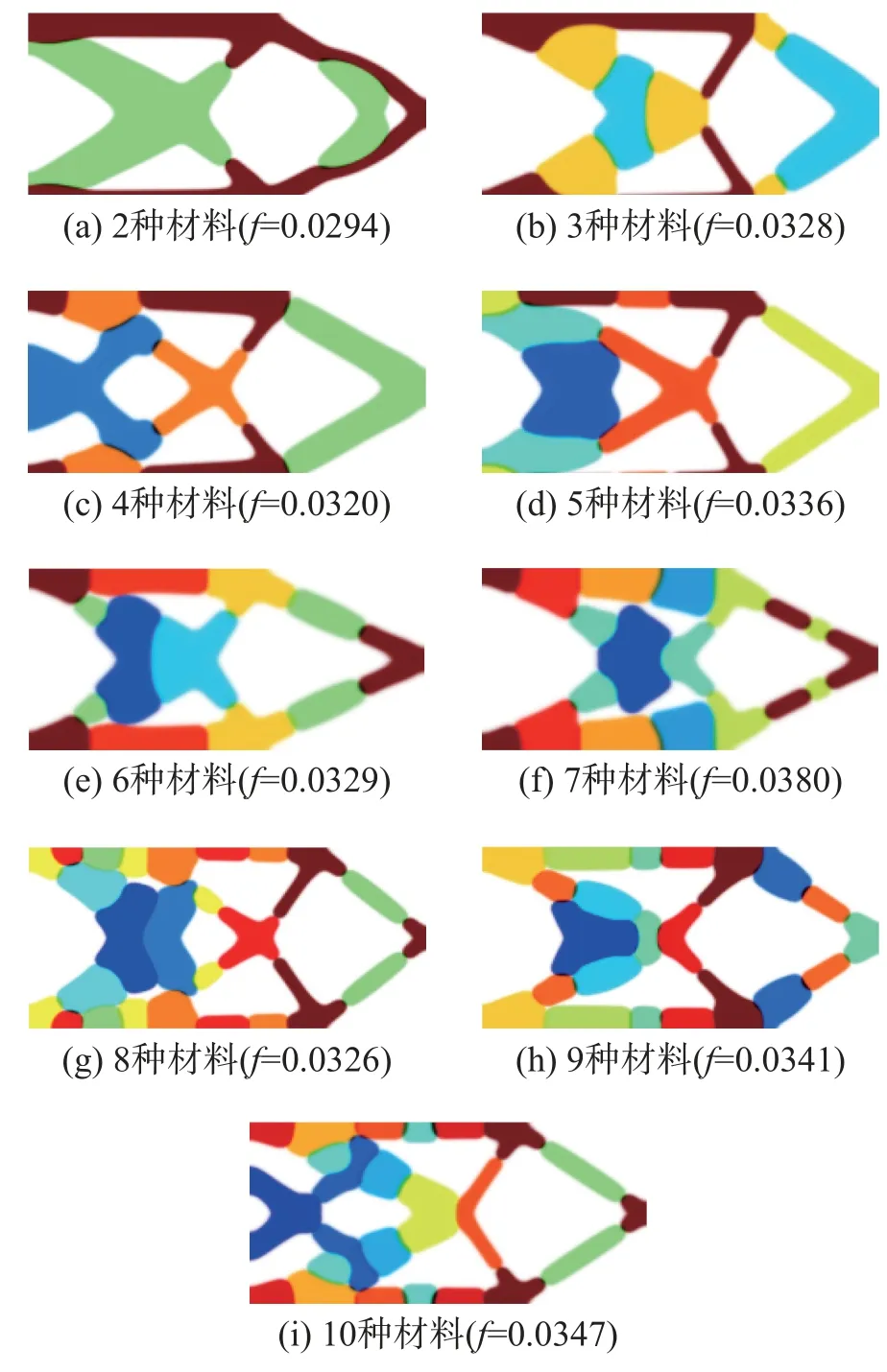
图7 悬臂梁的多材料拓扑优化Fig.7 Multi material topology optimization of cantilever beam
图8 为悬臂梁多材料最优拓扑的动柔度时间历程,多相材料设计的动柔度变化基本一致,平均动柔度几乎相同(如图7 所示)。由于7 相多材料设计的最软相材料位于内部加强肋的交叉点处,使结构的平均动柔度高于其他多相材料设计。
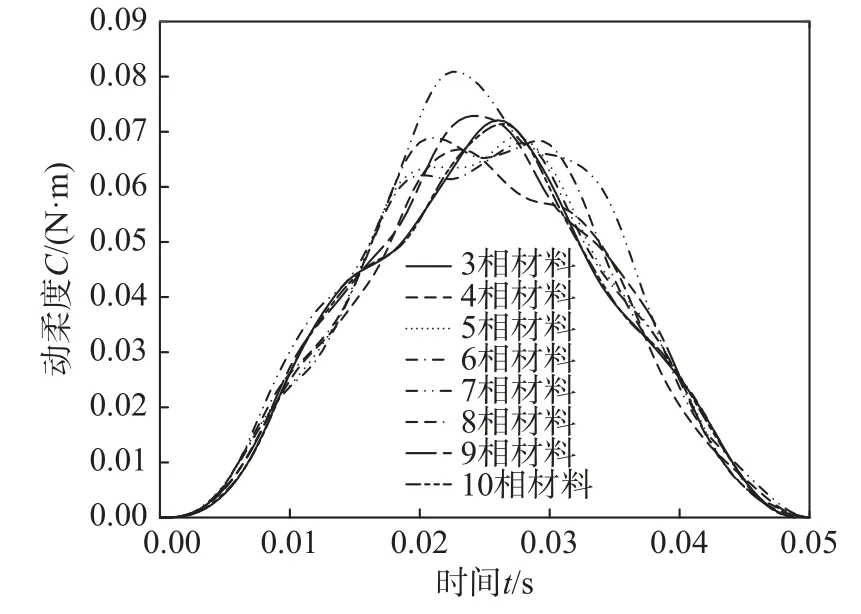
图8 悬臂梁多材料最优拓扑的动柔度时间历程Fig.8 Time history of dynamic flexibility for optimized multi-material topology of cantilever beam
3.2 简支梁
如图9 所示,简支梁上端自由边中点处承受余弦半波载荷f(t)=f0cos(πt/tf),载荷幅值f0=1 kN,初始设计域的结构尺寸为:L=12 m,H=2 m,h=0.01 m。多相材料的基准弹性模量E0=200 GPa,任一材料相的泊松比νi=0.3,密度ρi=7800 kg/m3,瑞利阻尼参数αr=10 ,βr=1×10-5。
图9 简支梁Fig.9 Simply supported beam
图10 为不同载荷持续时间工况下双材料简支梁问题的优化设计结果。3 种工况的优化拓扑皆是由两侧支撑杆和中间环型结构组成,但是两相材料分布迥然不同。静力学工况的优化拓扑在中间环型结构处集中了高弹性模量材料,因而它的动刚度大于动力学工况优化拓扑的动刚度;但是,动力学工况的优化拓扑在两侧支撑杆集中了高弹性模量材料,能够进一步抑制惯性载荷的影响,致使其动刚度大于静力学工况优化拓扑的动刚度。如图11 所示,静力学工况的位移与动柔度响应介于两种动载荷工况优化拓扑的相应动响应之间,验证了前面的结论。另外,随着动力学载荷作用时间的减少,阻尼对于结构的能量耗散作用有所减弱。

图10 双材料简支梁问题动静态载荷优化结果对比Fig.10 Comparison of dynamic and static load optimization results of bimaterial simply supported beam
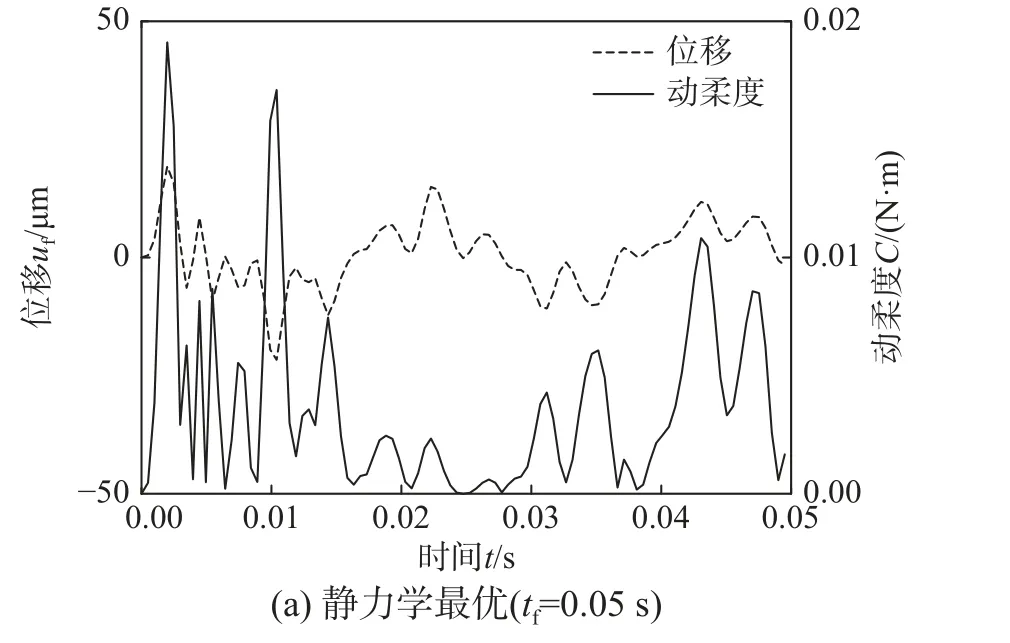
图11 最优简支梁载荷作用处垂向位移和动柔度时间历程Fig.11 Time history of vertical displacement and dynamic flexibility at the loading point of the optimal simply supported beam structure
图12 为tf=0.05 s 时简支梁的多材料拓扑优化结果,多相材料设计的平均动柔度基本一致。多相材料结构的整体拓扑基本一致,中间环型强化结构有所差异,特别是4 种材料、6 种材料和10 种材料的优化拓扑差异显著。随着材料相数目的增加,中间环型强化结构的下端桁架部分布置更多的低弹性模量材料,两侧支撑杆结构布置更多的高弹性模量材料,使两者能够达到刚度的最优匹配。
3.3 L 型结构
如图13 所示,L 型结构右侧自由边中点处承受正弦半波载荷f(t)=f0sin(πt/tf),载荷幅值f0=1 kN,初始设计域的结构尺寸为:L1=H2=12 m,L2=H1=18 m,厚度h=0.01 m。相材料的基准弹性模量E0=200 GPa,任一材料相的泊松比νi=0.3,密度ρi=7800 kg/m3,瑞利阻尼参数αr=50 ,βr=3×10-5。
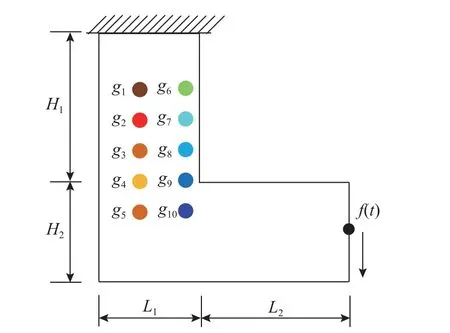
图13 L 型结构Fig.13 L-shaped structure
图14 为不同载荷持续时间工况下双材料L 型结构问题的优化设计结果。动力学工况的优化拓扑在内侧直角应力集中处分布了更多的高弹性模量材料,而静力学工况的优化拓扑在直角拐角处增加了加强筋强化结构。与静力学优化拓扑相比,动力学最优拓扑在载荷作用点附近分布了更多的材料,特别是外侧的三角形构型具有更大的截面尺寸,因而具有更大的动刚度。如图15 所示,静力学工况的位移与动柔度响应均高于动载荷工况,其动刚度偏低,从而验证了前面的假设。另外,动力学tf=0.05 s工况下的优化拓扑在内侧直角处堆积了更多的高弹性模量材料,使得其动刚度大于tf=0.03 s工况下优化拓扑的动刚度。
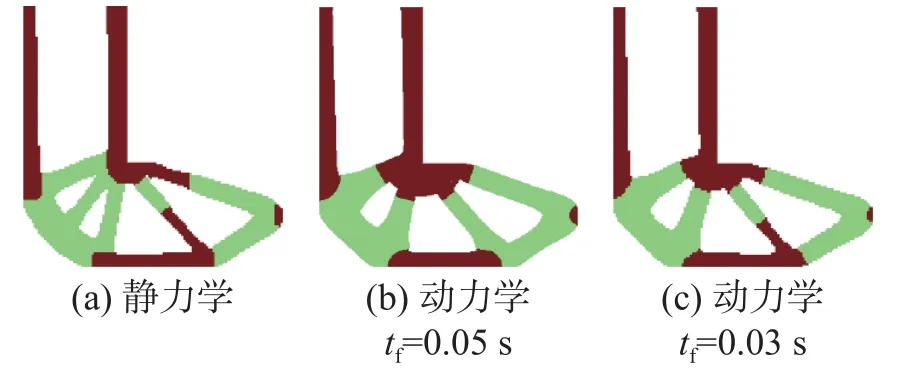
图14 双材料L 型结构问题动静态载荷优化结果对比Fig.14 Comparison of dynamic and static load optimization results of bimaterial L-shaped structure

图15 最优L 型结构载荷作用点处的垂向位移和动柔度时间历程Fig.15 Time history of vertical displacement and dynamic flexibility at the loading point of optimal L-shaped structure
图16 为tf=0.05 sL 型结构的多材料拓扑优化结果。多相材料结构的整体拓扑构型基本一致,载荷作用点附近的三角形构型的强化方式为:增加内侧棱边的截面宽度和内部添加加强筋。随着材料相数目的增加,高弹性模量材料分布于固定端垂向平行杆附近,低弹性模量材料分布于载荷作用点附近的三角形构型。但是,由于上述两种强化作用,致使载荷作用点附近的三角形构型与固定端垂向平行杆构型能够达到刚度匹配,从而保证整体结构的动刚度最优。对于6 相和10 相多材料设计,最软相材料位于载荷作用点附近的三角形构型的内部棱边,致使结构的平均动柔度均高于其他多相材料设计。

图16 L 型结构的多材料拓扑优化Fig.16 Multi-material topology optimization of L-shaped structure
3.4 Michell 型悬臂梁
如图17 所示,Michell 型悬臂梁右侧自由边中点处承受正弦半波载荷f(t)=f0sin(πt/tf),载荷幅值f0=1 kN,初始设计域的结构尺寸为:L=5 m,H=4 m,h=0.01 m,R=1 m。多相材料的基准弹性模量E0=200 GPa,任一材料相的泊松比νi=0.3,密度ρi=7800 kg/m3,瑞利阻尼参数αr=2.5 ,βr=4.5×10-4。
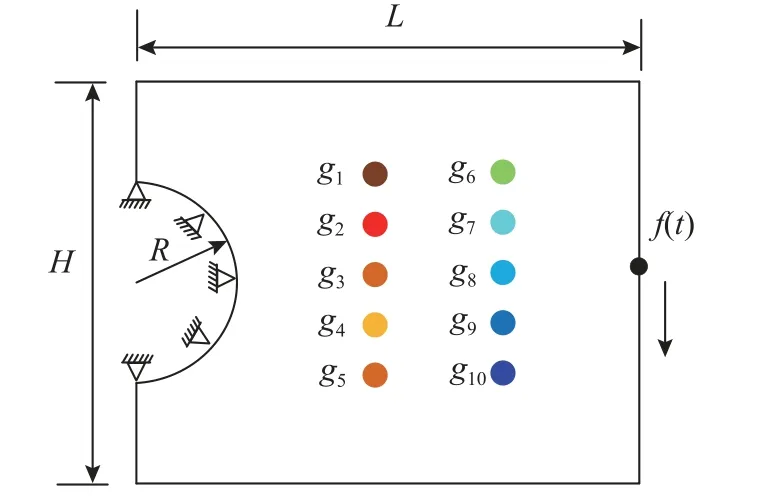
图17 Michell 型悬臂梁Fig.17 Michell cantilever beam
图18 为不同载荷持续时间工况下双材料Michell 型悬臂梁问题的优化设计。与静力学工况的优化设计相比,动力学工况的优化拓扑内部加强肋的具有更大的截面尺寸,载荷作用点附近聚集了更多的高弹性模量材料,因而后者具有更高的动刚度。此外,动力学tf=0.05 s工况下的优化拓扑内部加强肋的宽度尺寸较大,其方位更接近于垂向,有利于抑制动载荷作用下的变形,相对于tf=0.03 s工况下优化拓扑具有更高的动刚度。如图19 所示,静力学工况的位移与动柔度响应均高于动载荷工况,其动刚度偏低,而动力学tf=0.05 s工况的上述动响应最低,其动刚度最高,与优化拓扑的分析结果一致。

图18 双材料Michell 悬臂梁问题动静态载荷优化结果对比Fig.18 Comparison of dynamic and static load optimization results of bimaterial Michell cantilever beam
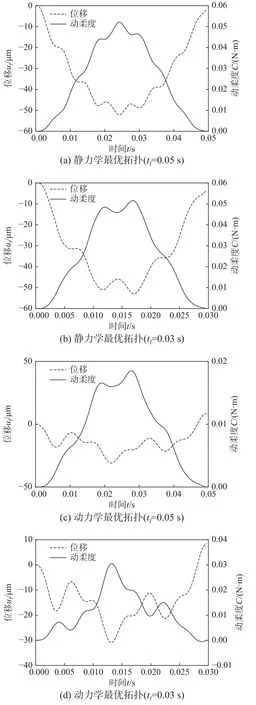
图19 最优Michell 型悬臂梁结构载荷作用点处的垂向位移和动柔度时间历程Fig.19 Time history of vertical displacement and dynamic flexibility at the loading point of optimal Michell cantilever beam structure
图20 为Michell 型悬臂梁的多材料拓扑优化结果。外环拓扑极为相似,内部强化构型差异显著。高比例的硬材料分布于外部拓扑,而软材料在内部联接于内部拓扑。另外,载荷作用点附近也集中了高弹性模量材料,抵消惯性载荷的动态影响。对于9 相和10 项多材料设计,最软相或次最软相材料位于载荷作用点附近的三角形构型的内侧棱边,致使结构的平均动柔度均高于其他多相材料设计。
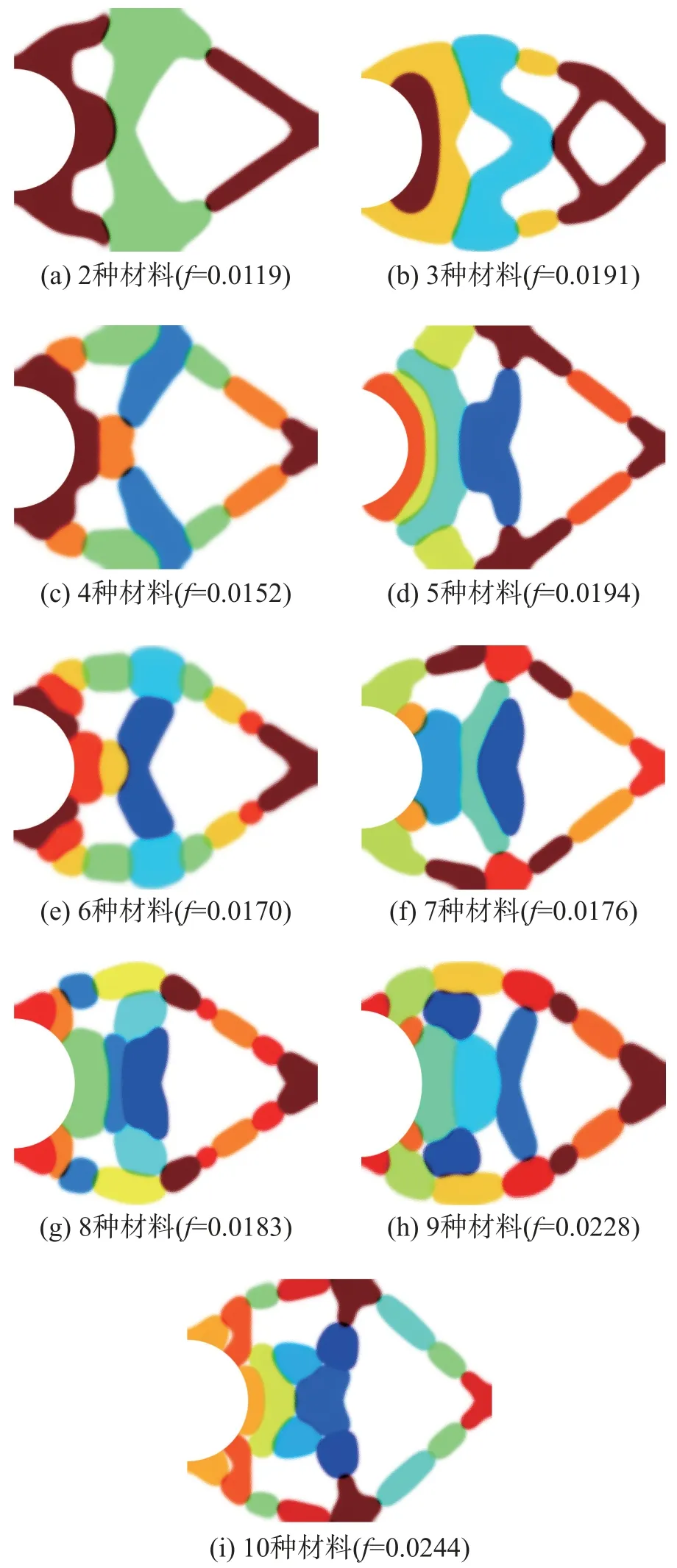
图20 Michell 型悬臂梁的多材料拓扑优化Fig.20 Multi-material topology optimization of Michell cantilever beam
4 结论
本文基于多分辨率-多边形单元建模策略,提出了求解多材料结构动响应问题的拓扑优化方法,研究结论如下:
(1) 通过悬臂梁、简支梁、L 型结构和Michell型悬臂梁等典型数值算例,验证了所提多材料结构时域动刚度拓扑优化方法的可行性。
(2) 动态载荷的作用时间对于优化结果具有重要的影响。随着载荷作用时间的减少,结构内惯性力的影响更加显著,致使多材料结构的优化拓扑存在明显的差异。
(3) 将本文所提出的多材料结构动力学优化方法延伸至超材料结构的动力学设计问题,可以实现高分辨率胞元-宏观结构构型的动力学多尺度协同优化设计。
基于提出的动力学多材料拓扑优化框架,作者将在后面工作中考虑动力学载荷作用下多材料之间的界面损伤与解耦,提出多材料结构界面失效问题的动力学拓扑优化方法。
