单圈图的Steiner k-general Wiener指数

王 笑,耿显亚

(安徽理工大学 数学与大数据学院,安徽 淮南232001)

本文中所研究的图都是简单、有限和无向的.本文所用的符号和术语请参考文献[1].设G是一个至少2阶的连通图,S是G的非空顶点集,则Steiner距离d(S)表示G中包含点集S的最小连通子树的边数.如果G的子图T是树并且S⊆V(T),则称T是S的Steiner树或S-Steiner树.Steiner树在计算机网络中有广泛的应用,有关Steiner距离的更多详细信息,请参考文献[2-6].

拓扑指数是一种由化合物结构导出的数学不变量,常用于描述有机化合物的物理、化学和药理特性,其中Wiener和Steinerk-Wiener指数是两个重要的拓扑指数,在对化学的研究中,它们是研究有机化合物结构关系的有用工具.2016年Li等[7]将Wiener指数推广到Steinerk-Wiener指数,并确定了一些特殊图类的Steinerk-Wiener指数的计算式及树的Steinerk-Wiener指数的上下界,有关Steinerk-Wiener指数的更多研究,请参考文献[8-15].本文进一步推广了Steinerk-Wiener指数,给出Steinerk-general Wiener定义以及单圈图的下界,并得到对应的极图.

1 基本概念

定义1[3]对于S⊆V(G),点集S的Steiner距离d(S)表示G中包含点集S的最小连通子树的边数,即

d(S)=min{|E(T)|:T是G的子树S⊆V(T)}

定义2[8]Steinerk-Wiener指数定义为

当k=2时,Steiner 2-Wiener指数就是wiener指数.

定义3 Steinerk-general Wiener指数定义为

特别地,当m=1时,Steinerk-general Wiener指数就是Steinerk-Wiener指数.

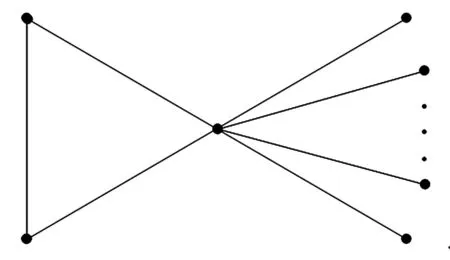
图1 图C3(Sn-2)

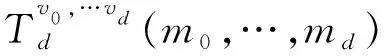
2 主要结论

设G,H是两个非平凡的连通图,且u∈V(G),v∈V(H),设GuH是通过用v重合u从G和H中获得的图.

引理2.1 设G是一个非平凡的连通图,且u∈V(G),Tm是一个非平凡的树(m阶),且v∈V(Tm),通过删除Tm的边从GuTm获得GuSm并将Tm/{u(v)}的顶点连接到u(v)上,k是一个整数,当2≤k≤n-2时,则有

当且仅当GuTm≅GuSm时等号成立.

证明对于任意的S⊆V(GuTm)=V(GuSm),|S|=k,下面分3种情况讨论.

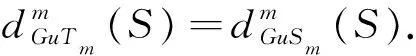
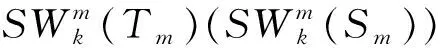
通过反复应用引理2.1的计算,得到以下推论.

推论 2.1 令G=Ct(Tt1,Tt2,…,Ttc)≠Cn,k是一个整数,且2≤k≤n-1,则有

当且仅当G≅Ct(St1,St2,…,Stc)等号成立.

引理2.2 设Ct(St1,St2,…,Stc)≠Cn,k是一个整数,且2≤k≤n-1,则有

当且仅当(Ct(St1,St2,…,Stc))≅C3(Sn-2)等号成立.

证明令G=Ct(St1,St2,…,Stc),将G和C3(Sn-2)的顶点集表示为V(G)=V(C3(Sn-2))={u0,u2,…,un-1},其中u0是G割点,是C3(Sn-2)唯一一个n-1度顶点.对于任意S⊆V(G),|S|=k,Steiner树TG(S)是毛毛虫树.

引理2.3 设k是一个正整数,且3≤k≤n-2,则

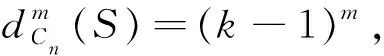
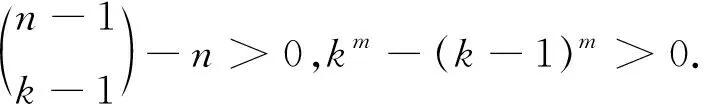
定理2.4 对于G∈UC(n)(n≥6),k是一个整数,且3≤k≤n-2,则有

当且仅当G≅C3(Sn-2)时等号成立.

3 结 语

在现有国内外专家研究的基础上,本文进一步推广了Steinerk-Wiener指数,给出了单圈图的Steinerk-general Wiener指数的下界,并确定了下界时的极图,为接下来关于Steinerk-Wiener的更多研究提供了思路.