颗粒混凝土冲击压缩动态力学特性试验研究
2024-02-24韩国庆穆朝民陆显峰时本军
韩国庆,穆朝民,陆显峰,王 阔,时本军
(1.安徽理工大学 安全科学与工程学院,安徽 淮南 232001;2.安徽理工大学 土木建筑学院,安徽 淮南 232001;3.陆军工程大学 爆炸冲击防灾减灾国家重点实验室, 南京 210007)
颗粒混凝土是一种密度小、孔洞密集、均质缓冲吸能性能强的轻材质.EPS是一种常见材料,将其应用到混凝土制作可降低成本,在抗震、绝热、绝缘和耐水方面有很好的性能,还兼备耐腐蚀性强的特性[1].近年来在实际工程中已得到一定的应用,在静力学方面,人们对颗粒混凝土进行了相对较多的探究,但涉及到其冲击力学特性的实验甚少.当下关于颗粒混凝土材质的力学研究多关注于材质改良及静态力学特性,如胡国峰和罗玉财[2-3]研究了EPS轻质混凝土制作流程,同时测出其静态抗压强度;于周平,刘凤利和李红超[4-6]研究了纤维对EPS混凝土力学性能的影响,得出掺入纤维可以在一定程度上改善混凝土的力学性能.管洪涛[7]等探索了EPS水泥复合材质的吸波性能与抗压特性,得出EPS添补水泥基体复合材质有较好的吸波特性,同时其添补率和颗粒大小对材料的吸波影响极强.胡艳丽[8]等研究了泡沫轻质混凝土与孔结构的关系,得出结论:轻质混凝土强度受孔大小影响,其中孔径离散度越小,强度越高,孔的形态对其特性影响较小.曹军平和李碧雄[9-10]借助正交实验方法,得到综合性能最佳的EPS轻型混凝土基础配合比.Laukaitis、Roy和GaneshBabu[11-13]探究了颗粒大小对EPS强度的影响.DucHoangMinh和K·Miled[14-15]等研究结果表明EPS结构混凝土的基体的骨料尺寸、EPS结构混凝土密度对其和易性、抗压强度等性能有影响,其中减小基体骨料粒径对提高其工作性和抗压强度的非常显著,而EPS混凝土的密度从1 400~2 000 kg/m3,抗压强度可增强到20 MPa.在动力学性能研究方面,PHBISCHOFF[16]等发现EPS混凝土在应力冲击作用下产生了较大变形,在此过程中反射和吸收大量能量,具备较强的吸能特性,可较好用在结构抗爆方面.其他研究发现对于采集波阻抗小的材料应采用灵敏系数比较高的应变片,对轻质混凝土恒应变率的冲击压缩试验.吴继囡[17]等围绕再生EPS颗粒对C40混凝土抗压强度的影响开展了试验研究,试验结果表明,掺入EPS颗粒的C40混凝土结构随颗粒直径的增加强度损失增加.李森森[18]等研究了不同EPS颗粒含量与不同EPS颗粒粒径对EPS混凝土抗压强度的影响.试验结果表明:随EPS颗粒含量增加,EPS混凝土的密度、强度降低.EPS颗粒粒径对EPS混凝土的密度及力学性能影响较小.于周平[19]等通过试验分析了聚苯颗粒混凝土破坏形态,研究混凝土密度、砂率和粗集料替代率对抗压强度的影响.结果显示聚苯颗粒混凝土的抗压强度随着随砂率、混凝土密度的增大而增大.Li等[20]对5种不同橡胶掺量和粒径的橡胶混凝土进行了试验.研究了橡胶对混凝土力学性能的影响,提出了适用于低橡胶掺量混凝土的改进本构模型.因此,对颗粒混凝土开展多种速度下动态压缩试验,获得应力峰值与应变率关系.本文使用SHPB研究颗粒混凝土在动态力学方面的特性,建立了颗粒混凝土峰值应力前和峰值应力后动态应力-应变的等效本构方程.
1 颗粒混凝土试样制备和SHPB
1.1 颗粒混凝土试样制备
颗粒混凝土(KL)是将水泥、微硅粉、水、石、砂和颗粒按表1配置,借助模具定型.对于素混凝土(S)使用C50.两种混凝土均做成Φ75 mm,高度为35 mm的试样,其物理参数见表2.

表1 颗粒混凝土配合比(单位:kg/m3)Table 1 Mix proportion of granular concrete

表2 物理参数Table 2 Physical parameters
1.2 SHPB装置
本系统的杆件为Φ75 mm SHPB,杆件示意图见图1.其中实验系统的撞击杆、入射杆、透射杆和吸收杆直径均为75 mm,长分别为400、4 000 mm和2 500 mm,材质均为高强度合金杆,杨氏模量为70 GPa,纵波波速为5 090 m/s.

图1 SHPB压杆装置示意图Figure 1 Schematic diagram of SHPB pressure rod device
1.3 数据处理
SHPB通常采用二波法[21]来处理实验数据,本文就使用经典二波法入射波及透射波计算出试样对应不同应变率下应力-应变关系,见式(1):
(1)
其中:E为对应杆的杨氏模量,A、A0分别为对应杆和试样的端面面积,C为波在对应杆中的速度,εi(t)为入射应变脉冲,εt(t)为透射应变脉冲,L为试样高度.
图2所示为碰撞期间颗粒混凝土两端的应力平衡曲线,入射、反射应力之和与透射应力基本相等,颗粒混凝土两端应力平衡可以得到满足,表明所得试验结果具有可靠性.
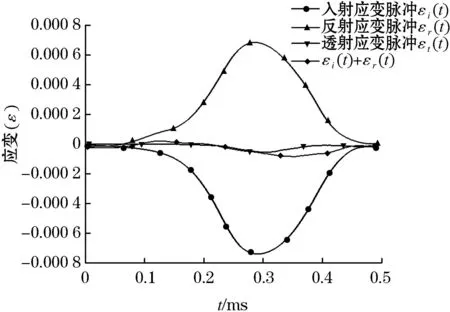
图2 颗粒混凝土实验波形Figure 2 Experimental waveform of granular concrete
2 试验结果分析
2.1 应力应变曲线和破坏形态
由图3可得到:1)伴随应变率变大,颗粒混凝土的应力-应变曲线呈现显著的差异,应力峰值、动态弹性模量均增大,整体表现出初始弹性段、较短的平台变形段和应变软化段,较短的平台变形段下的应力值较低,在3MPa以下;2)在464.71 s-1下,颗粒混凝土的应力与应变卸载段曲率存在转折处,在转折处之后应力平台显著.颗粒混凝土是由聚苯颗粒和混凝土混合制成的一种新材料.在加载变形过程中,颗粒和混凝土微孔洞彼此接触,混凝土微孔洞构造的侧向束缚和颗粒本身的应变率效应加强,其强度和颗粒材料比很大程度变强.伴随应变率变大,1)混凝土材料和聚苯颗粒材料的应变率效应提高均有表现,带来混凝土微孔洞结构在最开始时的支撑力有很大程度的提高;2)裂隙的扩展也引起混凝土微孔洞构造在很小的压缩情况下发生脆性断裂.在混凝土微孔洞崩塌下,才能对颗粒产生挤压变形,可呈现出显著的吸收能量的特性,在应力-应变图像中表现在卸载段的平台上.在图4(A)、(B)、(C)在最后毁坏外形上,可看出颗粒混凝土试样被压扁,但外形保持完整,呈现出清晰的可延性.如图4(D),随着应变率增加,颗粒混凝土破碎呈絮状.

图3 不同应变率下的颗粒混凝土试样的应力-应变曲线Figure 3 Stress-strain curves of granular concrete specimens under different strain rates

图4 颗粒混凝土试件破坏的形态Figure 4 Failure morphology of granular concrete specimens
为了剔除实验过程的误差对测得数据影响,也作为与颗粒混凝土参考组,使用了一组素混凝土SHPB作为对照组,其应力-应变曲线见图5.刚开始曲线呈上凹型,原因是由于素混凝土原本裂隙和孔洞在压力作用下慢慢的合拢所致,合拢之后,曲线可看作线性关系,持续加载下,裂隙在原裂隙基础上扩大,部分毁坏加剧,直至屈服极限,同时曲线斜率变小,试样切线模量也渐渐变小,接着迅速步入应变软化过程.剔除实验过程的误差,与素混凝土应力-应变图像对比,发现颗粒混凝土存在两个突出特征:1)曲线凹凸变化较大,在毁坏过程特别显著;2)应变软化期间应力大小并没有迅速降低直至几乎没有支撑力,而是存在了一个较高的应力平台的阶段,同时随着应变率的变大,应力平台阶段呈现出变长的趋势.
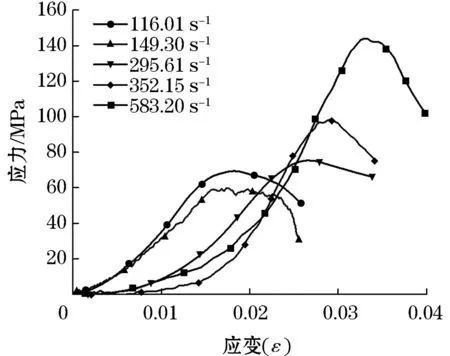
图5 素混凝土试件的应力-应变曲线Figure 5 Stress-strain curve of plain concrete specimens
2.2 抗压强度动力放大系数
在应变率较高的时候,混凝土材质抵抗压力的强度增长可以用动力放大系数DIF来体现:
(2)
其中:fc,d,fc,s分别表示试样单轴冲击作用下抗压强度和单轴静态抵抗压力的强度.
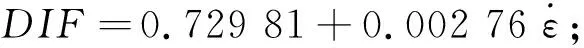

图6 动态增长因子随应变率变化趋势Figure 6 Trend of dynamic growth factor with strain rate
3 动态本构关系
近年来,Z-W-T(朱兆祥、王礼立和唐志平)本构模型能够很好的反应岩土材料动态本构关系,得到学术界广泛的认可,同时被许多国内外科研工作者处理成另外一种形式来反映其他材料的本构模型[22-24],但原理有异曲同工之妙.“Z-W-T”(朱兆祥、王礼立和唐志平)本构模型是由中国专家朱兆祥、王礼立和唐志平研发出来的,提出的初衷是想建立固态分子的动态力学关系,具体形式见式(3):
(3)
其中:α、β、E0为弹性系数;E1、E2为麦克斯韦体的弹模量;θ1、θ2为松弛时间.对于Z-W-T本构模型,可以通过以下模型反应,见图7.
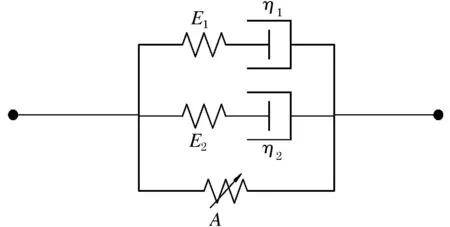
图7 “Z-W-T”本构关系Figure 7 "Zhu-Wang-Tang" constitutive model
Z-W-T本构模型方程一共分为两大项,对于第1项而言,是指平衡状态下的应力,E0具体含义是系统平衡下的弹性模量,其应变率效应可以忽略不计;Z-W-T本构模型方程的第2项具体含义是θ1和θ2差值较远的麦克斯韦体松弛关系;麦克斯韦在θ1时具体含义是反应某种材质在应变率比较小情况下的力学行为,同时发现有一种规律,在应变率比较小情况下材质的力学行为会伴随应变率增大而增大,θ1远远大于通过实测得到的时间,麦克斯韦体在较小频率状态下不会松弛,体现出线性弹簧过程;麦克斯韦在θ2时具体含义是反应某种材质在应变率比较大情况下的力学行为同时也发现有一种规律,伴随应变率降低,θ2远远小于通过实测得到的时间,麦克斯韦体在较大频率状态下将全部松弛,有黏壶模型的特性,发现较高频率的麦克斯韦的力学行为消失了,等价于无.
前人对各种固体材料本构关系已经做了许多探究并给予相应的方程式,基于这些专家研究之上,通过其应力与应变图像反映出应变、应变率硬化等特殊材料规律,Z-W-T本构模型可以更具有针对性对前面描述的动态力学行为做出更科学说明,Z-W-T本构模型式如下:
(4)
通过实验中得到的动态冲击下相关力学性能和Z-W-T(朱兆祥、王礼立和唐志平)明确的物理量的意义,做出更具有科学的简化:
等式的第一项σE=E0ε+αε2+βε3,反映在冲击作用下材质的平衡状态下的力学行为,可以忽略应变率带来的影响,通过实际实验场景,混凝土发生的变形特别小,借鉴过往学者专家的成果,将把非线性的弹簧给予线性化了,再将σE=E0ε+αε2+βε3中的三次方变为一次方,进一步得到:σ0=E0ε,原本的Z-W-T(朱兆祥、王礼立和唐志平)本构关系简化为线性弹簧.简化的Z-W-T(朱兆祥、王礼立和唐志平)本构模型式见式(5).
(5)
颗粒混凝土和普通混凝土微观结构通过电子显微镜发现混凝土的结构中有较大量的毛细孔和分布较广的裂隙,同时发现材质骨料分布没有规律不均匀,对于观察到的裂隙和毛细孔空间位置也是不明确的未知的,由于这些未知的信息非常多,但是这些信息又是客观存在的,所以在对混凝土建立动态冲击下的本构关系不能忽略这些信息,需要考虑这些客观存在现象,混凝土微观结构中毛细孔和分布较广的裂隙随机发展毫无规律可寻,为了更好地建立该模型同时去繁从简原则,借助连续损伤力学处理模式,将混凝土的材质看作均匀分布的物体,引入损伤这一物理量D来判定砼材质的破坏大小,参照Lemaitre应变等效理论,该损伤关系式见(6).
σa=(1-D)σr
(6)
其中:σa为有效应力;σr为原始应力;D为损伤物理量.
根据前人的研究成果结合现场实验现场发现,冲击气压越大,应变率相应增大,混凝土损伤的严重,碎块就越细,由块状、碎块状最后变成细粉末状,结合现场实验现象发现混凝土的破损是受应变率影响.将混凝土在施加动载冲击下的损伤与应变率和应变综合在一起,将混凝土的损伤发展等式写成式(7).
(7)

综上分析,混凝土的冲击作用下本构关系描述成式(8).
(8)
可以把霍普金森杆下应变率看成恒应变率,从而简化的Z-W-T(朱兆祥、王礼立和唐志平)本构模型描述见式(9).
(9)
根据简化的Z-W-T本构模型(9)对103.88、 195.43、 262.94 s-1和448.88 s-1四种应变率下颗粒混凝土峰前后冲击作用小计算出的应力-应变曲线借助ORIGIN绘图软件进行数值曲线拟合,圈曲线是实验测得,红色曲线是通过简化的Z-W-T本构模型(9)函数关系赋值拟合得到见图8,待确定的参数见表3,其中R2均在0.99附近,由图8可知,两曲线有很好的吻合度.

图8 颗粒混凝土的试验和拟合动态应力-应变曲线Figure 8 Experimental and fitted dynamic stress-strain curves for foam concrete

表3 颗粒混凝土简化的Z-W-T拟合参数Table 3 Simplified Z-W-T fitting parameters of granular concrete
4 结 论
1)随着应变率增大,颗粒混凝土的应力-应变曲线出现明显的差异,应力峰值,动态弹性模量均增大,整体表现出初始弹性段、较短的平台变形段和应变软化段,较短的平台变形段下的应力值较低,在3 MPa以下.在混凝土微孔洞崩塌下,颗粒才被压缩,可表现出明显的吸收能量的性能,在应力-应变曲线上体现在卸载段的平台上.在最后破坏形状上,可看出颗粒混凝土试样被压扁,但形状基本完整,表现出显著的可延性.
2)颗粒混凝土的动态抗压强度相比于普通混凝土低了将近两个数量级.素混凝土DIF拟合直线斜率大于颗粒混凝土的,即虽然两种混凝土都呈现出了显著的应变率效应,但颗粒混凝土对应变率的敏感性不及素混凝土.
3)该本构方程优点是针对反映颗粒混凝土峰值前后信息的方面取得了明显改善.本文对颗粒混凝土构建出对应的本构方程,改进了Z-W-T本构关系,建立了A、α、β、E0、E1、θ1、E2和θ2共八个参数的颗粒混凝土动态本构关系,拟合出103.88、195.43、262.94 s-1和448.88 s-1四种应变率下本构方程的八个参数值,实验数据和拟合数据具有较为明显的一致性,验证了本构方程的准确性.
