高温高应变率下钛合金Ti6Al4V 的动态力学行为及本构关系

杨 东，姜紫薇，郑志军

（1.安徽大学机械工程系, 安徽 合肥 230601；2.中国科学技术大学近代力学系, 中国科学院材料力学行为和设计重点实验室, 安徽 合肥 230026）

随着航空航天、国防工业等高端装备制造业的不断发展，对一些重要零部件材料的强度、硬度、热稳定性、耐腐蚀性等力学和机械性能的要求不断提高，促使钛合金材料的应用比例越来越高。然而，钛合金的机械加工却存在诸多难题，如加工过程中容易出现让刀、变形、振动等问题。探明钛合金在动态加载条件下的力学响应特性、获得率-热相关的本构模型对于优选其加工工艺具有重要意义[1]。

针对钛合金Ti6Al4V（TC4）的动态力学响应行为，国内外学者已开展了研究。Wang 等[2]采用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）技术对Ti6Al4V 试样进行冲击实验，研究了材料在不高于4 000 s-1的应变率范围内的断裂失效应变，发现断裂失效应变随着应变率的增大而减小。Longère 等[3]采用SHPB 技术获得了Ti6Al4V 在102～103s-1应变率下的剪切力学响应，发现随着应变率的升高，最大剪应变减小。Zhang 等[4]在3.9×103s-1的应变率下对Ti6Al4V 进行动态加载，发现微观断口形貌表现出韧窝区与平滑区交替分布的特征。张炜琪等[5]研究发现，Ti6Al4V 的流动应力存在明显的应变率强化效应，随着应变率的升高，失效应力逐渐增大，而失效应变逐渐减小。不同于准静态加载下的等温变形过程，钛合金的导热性能差使其在高应变率加载下的变形过程近似为绝热过程。Zhou 等[6]认为，随着应变率的增大，绝热温升引起的热软化成为影响材料变形的主导机制，并基于冲击加载实验数据构建了Ti6Al4V 的动态本构模型。陈敏[7]分析了应力状态、应变、应变率及温度对Ti6Al4V 力学性能的影响，并根据试验结果拟合出Johnson-Cook（J-C）本构模型。综合上述研究可以发现，针对Ti6Al4V 的动态力学行为研究主要集中在材料的强化和软化效应方面，关于材料在高温与高应变率耦合作用下的变形行为研究相对较少。此外，有研究表明，J-C 本构模型的精度随着应变率和温度的升高而降低[8]，材料在高温高应变率下的绝热温升效应不能忽视。

为此，本工作采用SHPB 技术研究Ti6Al4V 在高温高应变率加载条件下的动态力学响应，基于获取的实验数据，剖析其在高温高应变率下的流变应力特征、应变率增塑效应、微观组织变化及率-热敏感性，构建考虑绝热温升影响的本构模型，获得率-热相关的本构模型参数，为Ti6Al4V 在高速加工条件下的数值模拟及工艺参数优选提供理论依据。

1 实 验

实验用Ti6Al4V 为同批次锻坯块料。Ti6Al4V 为α+β 型钛合金，其原始金相组织的电镜图像如图1(a)所示。可以看出：初生α 相的颜色灰暗，呈等轴状，体积分数约为86.5%；β 相附着在等轴α 相上，色泽光亮。原始组织的晶粒尺寸分布和能量色散谱（energy dispersive spectroscopy，EDS）分别如图1(b)和图1(c)所示。可以看出，材料基体的晶粒尺寸分布不均，主要分布在8～18 μm 区间，平均尺寸为11.7 μm。

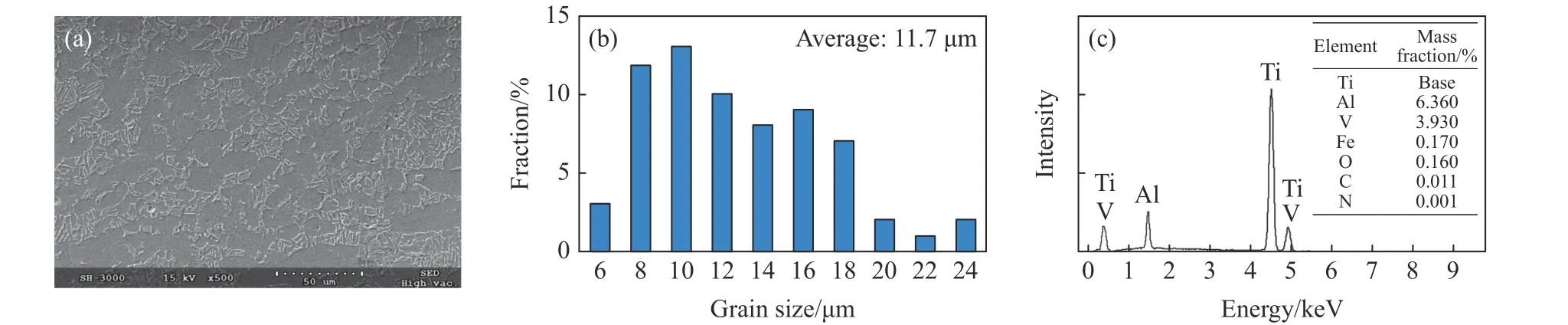
图1 钛合金Ti6Al4V 的初始金相组织(a)、晶粒尺寸分布(b)以及EDS (c)Fig.1 Original microstructure (a), grain size distribution (b) and EDS (c) of titanium alloy Ti6Al4V

室温准静态实验在EUT5105 电子万能试验机上进行。试样为直径8 mm、长8 mm 的圆柱体。参照GB/T 7314—2017《金属材料室温压缩实验方法》，采用恒应变率单向压缩试样，加载的应变率为10-3s-1，对应的加载速度为0.49 mm/min。为了保证实验数据的可靠性，进行3 次重复实验。

动态加载实验在SHPB 实验系统上完成。冲击试样为直径3 mm、长3 mm 的圆柱体，试样两端面抛光，表面粗糙度不大于0.8 μm。通过采集SHPB 系统入射杆和透射杆中的入射波应变εi、反射波应变εr和透射波应变εt信号，如图2 所示，基于一维应力波理论，计算得到材料的应力-应变曲线。所使用的SHPB 系统中，入射杆和透射杆具有相同的直径和长度，分别为8 和800 mm，撞击杆的直径和长度分别为8 和100 mm。

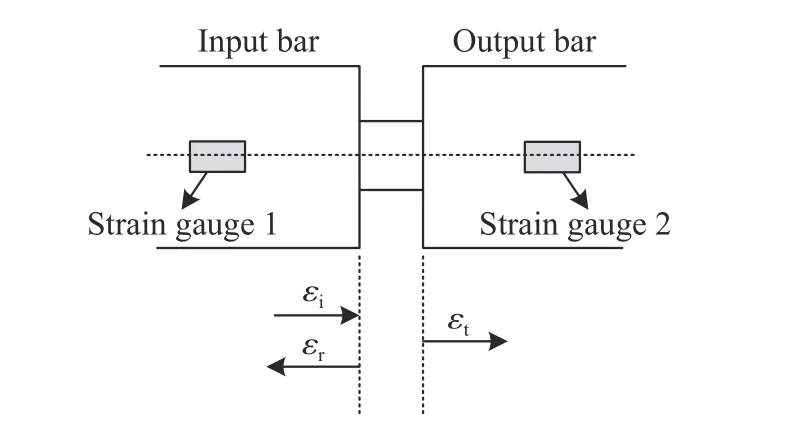
图2 应力波传播示意图Fig.2 Schematic diagram of stress wave propagation

冲击实验的初始应变率分别为2 000、3 000、5 000 和7 000 s-1。在进行高温SHPB 实验时，既要在试件上形成均匀稳定的温度场，还要尽可能地减少高温对入射杆和透射杆的影响。采用局部电阻丝快速加热法加热试样，通过程序将实验温度分别设定为25、100、200、400、600 和800 ℃。升温过程中，加载杆置于炉体外部。当温度到达指定温度后，通过计时器确定保温时间为10 min，保温结束时启动高温同步装置，通过高温同步装置在100 ms 内完成加载杆对试样的夹紧及冲击。每种工况下进行3 次重复性实验，取3 次实验数据的平均值作为实验结果。对回收试样沿轴向进行切割，采用2 000 目的砂纸打磨切割表面，经抛光处理后放入腐蚀液（HNO3、HF、H2O 的体积比为5∶3 ∶100）中保持10 s，采用金相显微镜观察变形试样的微观组织变化。

2 结果与讨论

2.1 流动应力特征

图3 为不同加载条件下钛合金Ti6Al4V 的真实应力-应变曲线。冲击加载初期，材料内部急剧的位错增殖使材料发生显著的应变硬化效应，宏观上表现为流动应力随应变增大而快速增大。随着应变的增大，当应变硬化效应与热软化效应达到动态平衡时，流动应力不再随应变的增大而发生明显变化，表现为应力-应变曲线的平台段，在此阶段流动应力稳步上升。随着变形量的进一步增大，晶格畸变能升高，位错密度降低，材料的软化效应增强。当达到材料的极限强度后，流动应力的增幅开始下降，直至材料失效[9]。

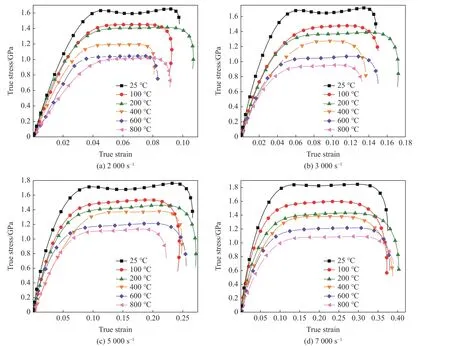
图3 Ti6Al4V 试样在不同温度和应变率条件下的真实应力-应变曲线Fig.3 True stress-strain curves of Ti6Al4V specimens at different temperatures and strain rates

从图3 还可以看出，在加载应变率相同的条件下，随着加载温度的升高，流动应力明显减小，材料呈现出明显的温度软化行为。高温促使材料的位错运动活跃，流动应力和动态屈服强度减小。图4 给出了率-热影响下Ti6Al4V 的动态屈服强度。在冲击加载应变率范围内，随着加载温度的升高，动态屈服强度降幅可达680 MPa。Ti6Al4V 还表现出显著的应变率强化效应，即相同的加载温度下流动应力随应变率的升高而增大，表现为屈服强度和强度极限随应变率的升高而显著增大。例如： 25 ℃时，强度极限由2 000 s-1时的1 683 MPa 增大至7 000 s-1时的1 822 MPa，这是因为高应变率下单位时间内塑性变形的增加需要更多的位错移动，加剧了金属内部的扭曲，位错相互纠缠形成割裂，使得位错滑移和扩散难度增加[10-11]。此外，随着应变率的升高，应变硬化效应减弱，表现为材料在塑性变形阶段的真实应力随应变增大的趋势逐渐放缓。高应变率下的材料变形过程可看作绝热过程，该过程中载荷作用时间极短，导致试样内塑性变形功转化的热能无法及时耗散，绝热温升与加载温度的共同作用导致试件产生热软化[12]。

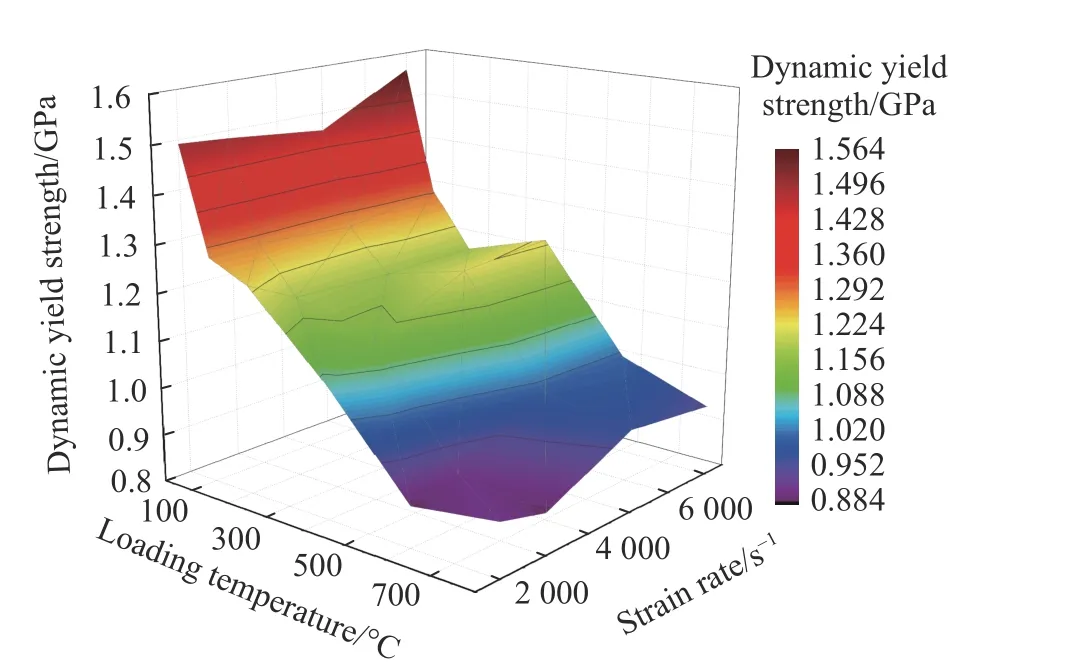
图4 率-热影响下Ti6Al4V 的动态屈服强度Fig.4 Dynamic yield strength of Ti6Al4V under the influence of strain rate and temperature

2.2 应变率增塑效应

从材料的真实应力-应变曲线可以看出，高应变率加载下Ti6Al4V 的最大塑性应变增量与应变率呈正相关。随着应变率的升高，应力-应变曲线的塑性流动趋势增强，塑性流动段显著变长，即高应变率下Ti6Al4V 表现出一定的应变率增塑效应。当加载温度为25 ℃，应变率为2 000、3 000、5 000、7 000 s-1时，最大塑性应变分别为0.06、0.10、0.18、0.24，增幅高达300%。这是因为高应变率加载极大地提升了变形孪晶密度，剧烈的变形孪生行为有利于激活滑移系。此外，Ti6Al4V 在高应变率加载下的绝热温升效应促使位错湮灭，降低位错滑移阻力，使材料内部发生软化。在变形孪生机制与绝热温升的共同作用下，Ti6Al4V 的塑性流动性提升，材料塑性增强。

Ti6Al4V 在绝热变形过程中的瞬态温升ΔT可表示为

式中：η 为塑性功热转换系数，对于高应变率变形过程，η 取0.9；ρ 为材料密度，取4 440 kg/m3；cp为比定压热容，25、100、200、300、400、500、600、700、800 ℃下Ti6Al4V 的cp分别为0.611、0.624、0.653、0.674、0.691、0.703、0.729、0.749、0.769 J/(g·K)[13]；σe为工程应力；εe为工程应变。

图5 显示了绝热温升随加载温度和应变率的变化。可以看出，在相同的加载温度下，绝热温升与应变率呈正相关。在相同的应变率下，绝热温升随加载温度的升高而下降，且在加载温度高于400 ℃时绝热温升降低的趋势不断放缓。当应变率大于5 000 s-1时，绝热温升响应曲线的斜率增大，表明绝热温升对加载温度的敏感程度增强，这是材料的cp随加载温度的升高而增大造成的。

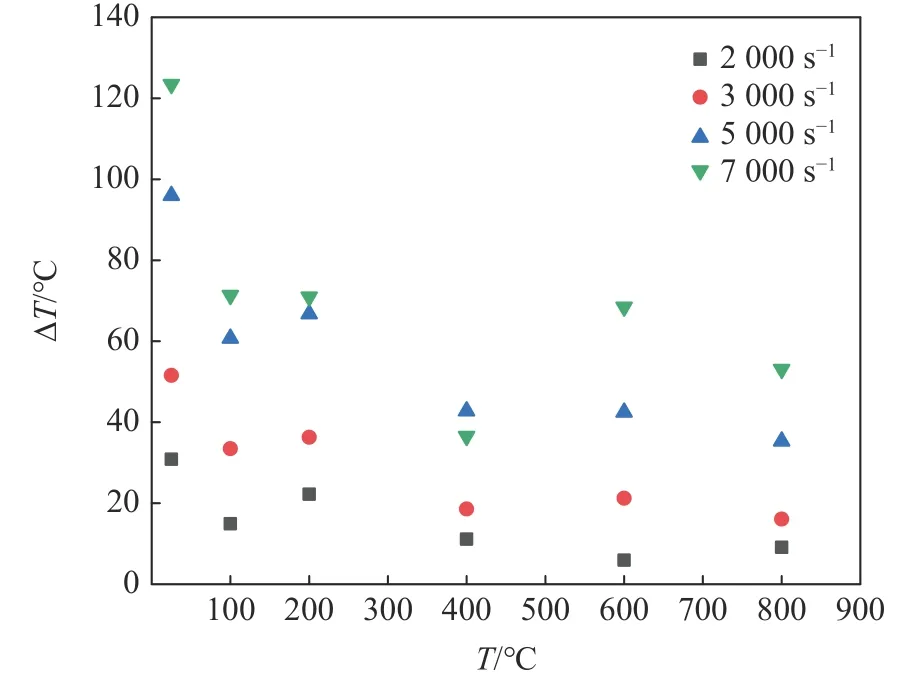
图5 绝热温升随加载温度和应变率的变化Fig.5 Variations of adiabatic temperature rise with loading temperature and strain rate

图6 为绝热温升（ΔT）以及加载温度-绝热温升耦合温度（T+ΔT）与试样的工程应变之间的关系。在本实验所研究的参数范围内，试样工程应变的最大值（0.315）出现在加载温度为800 ℃、应变率为7 000 s-1时，试样压缩变形最小值（0.092）出现在室温、应变率为2 000 s-1时。从图6 可以看出，随着绝热温升的升高，工程应变呈增大趋势。当绝热温升由最小值5.95 ℃（加载温度600 ℃，应变率2 000 s-1）升高到最大值123.43 ℃（加载温度25 ℃，应变率7 000 s-1）时，最大工程应变量由0.098 增大至0.313，增幅319%。加载温度-绝热温升耦合温度（T+ΔT）对试样最大工程应变的影响并不显著。

图6 ΔT 和T+ΔT 对试样工程应变的影响Fig.6 Influence of ΔT and T+ΔT on the engineering strain of specimens

2.3 微观组织变化

对变形试样沿轴向剖切，观察剖面的微观组织，可以发现，高应变率下，α 相沿加载轴向呈现出不同程度的压缩变形，其长宽比增大。如图7(a)和图7(b)所示，试件在高温预热、保温及高应变率冲击的综合作用下，热软化效应使拉长型α 相取代等轴α 相成为Ti6Al4V 微观组织的最典型特征。当加载温度达到600 ℃以上时，试样进入再结晶温度范围（600～800 ℃）[14]。在再结晶过程中，新的等轴α 相形成，如图7(b)所示，新生成的细小等轴α 晶粒的直径约为10 μm。达到Ti6Al4V 的再结晶温度后，回复过程中的热量主要通过空冷进行耗散，较长的耗散时间促使晶粒开始长大。晶粒长大有两种不同的形式：一种是冲击后Ti6Al4V 的压缩变形增大，应变诱发晶界迁移，大角度晶界向小角度晶界迁移；另一种是金相的选择性生长，金相仍维持原有的等轴形貌，但其尺寸与新生成的细化等轴α 相相比有明显的增大[15]。图7(c) 所示的α 相在应变能的作用下成组合并，形成直径大于50 μm 的块状α 相和拉长型α 相。图7(c)显示，生长后的等轴α 相晶粒尺寸达到25 μm。晶粒长大导致晶界减少，较低的晶界能导致晶体塑性变形抗力降低，在高温高应变率条件下试件的压缩变形显著增大。

图7 不同温度和应变率下Ti6Al4V 的微观组织Fig.7 Microstructures of Ti6Al4V at different temperatures and strain rates

2.4 率-热敏感性

为了定量描述材料的流动应力对应变率和温度的敏感性，采用温度敏感性因子ST和应变率敏感性因子Sε˙对Ti6Al4V 的率-热敏感性进行计算[16]。ST的表达式为

式中：T0为参考温度，σ0表示温度为T0时的真实应力，T为实验加载温度，σ 为当前条件下的真实应力。

图8 给出了Ti6Al4V 的ST随应变率 ε˙及温度T的变化（T0=25 ℃，ε=0.02）。从图8 中可以看出，所有工况下ST均为正值，表明Ti6Al4V 的温度敏感性与应变率呈正相关。当加载温度为100 ℃时，ST随应变率的升高而增大；当加载温度高于200 ℃时，ST随应变率的变化并不显著，表明在较高加载温度下应变率对ST的影响变弱。在同一应变率下，Ti6Al4V 的ST随加载温度的升高而显著降低，尤其当加载温度由100 ℃升高至200 ℃时，ST降低得最显著，表明Ti6Al4V 在该温度下的动态压缩力学行为受温度的影响最明显。当加载温度超过600 ℃时，ST的变化逐渐变缓。

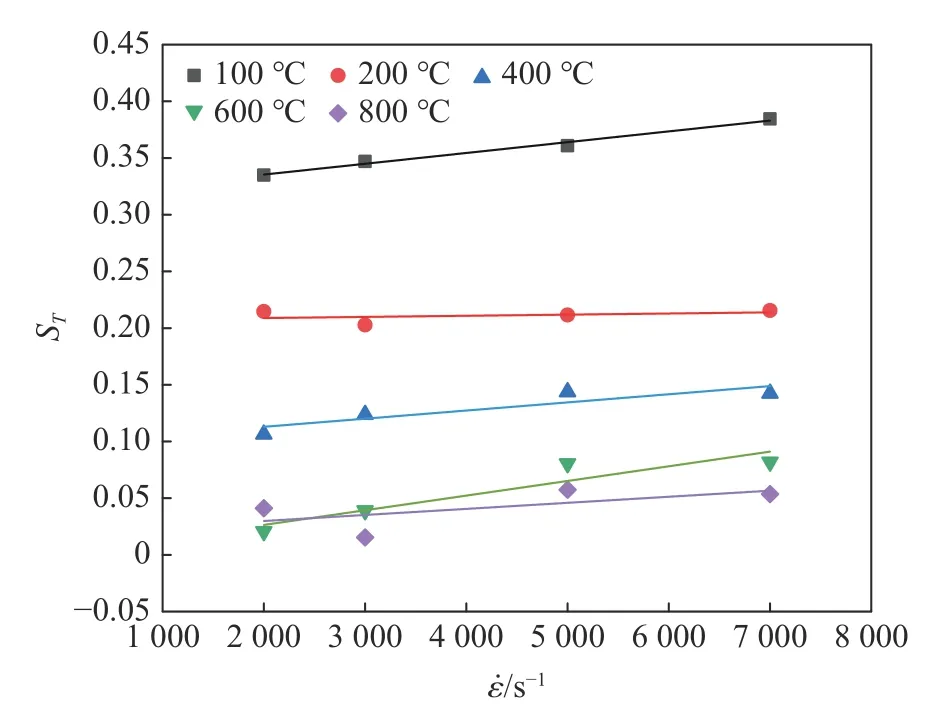
图8 不同加载温度下温度敏感性因子随应变率的变化（ε=0.02）Fig.8 Variation of temperature sensitivity factor with strain rate at different temperatures (ε=0.02)

图9 7 000 s-1 时应变率敏感性因子随真实应变的变化Fig.9 Variation of strain rate sensitivity factor with true strain at different temperatures ( ε˙0= 7 000 s-1)

Sε˙能够反映应变率对材料强化效应的影响程度，其表达式为

式中： ε˙ 为应变率； ε˙0为参考应变率，取0.001 s-1；σc为参考应变率下不同应变对应的真实应力。

3 动态本构模型

J-C 动态本构是一种唯象本构模型，其公式简单，且各部分含义明确，被广泛应用于金属切削加工等动态加载过程中材料的变形行为模拟。J-C 本构模型的表达式[17]为

式中：σf为材料的流动应力，A为准静态下材料的屈服强度，B为应变硬化系数，C为应变率强化系数，n为应变硬化指数，m为温度软化指数，εp为等效塑性应变， ε˙*为无量纲应变率，T*为相对温度，Tr为参考温度，Tm为材料熔点。J-C 本构模型表达式中等号右边3 项分别代表应变硬化项、应变率强化项和热软化项。

根据Ti6Al4V 在不同温度和应变率条件下的应力-应变关系，采用线性回归方法，可拟合得到其J-C 本构参数A、B、C、n和m。为获取A，在室温25 ℃、应变率为10-3s-1的条件下开展Ti6Al4V 的准静态压缩实验，将试样产生0.2%塑性形变时的应力作为材料的屈服强度，得到A=894 MPa。对B进行回归时，令J-C 本构关系中的应变率硬化项和热软化项为1，即参考温度取室温Tr=25 ℃，参考应变率取准静态加载应变率 ε˙0=10-3s-1，则式(4)可以转化为

对式(7)两端取对数，可得

通过线性回归拟合 ln(σf-A) - l nεp曲线，得到n=0.64，B=721 MPa。

对C进行回归时，令J-C 本构关系中的热软化项为1，将式(4)转化为

式中：σf的单位为MPa。

图10 对比了Ti6Al4V 在5 000 s-1、不同温度条件下的冲击压缩实验结果和J-C 本构模型预测结果。J-C 本构模型预测值较实验值总体偏小，且随着加载温度的升高，J-C 本构模型的预测误差逐渐增大。采用相关性系数R和平均相对误差δ 定量表征J-C 本构模型的预测精度，其计算公式[18]分别为

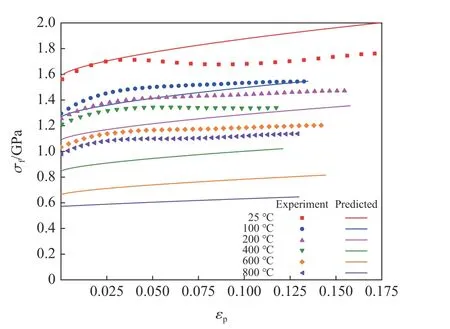
图10 实验数据与J-C 修正模型预测值的对比Fig.10 Comparison between experimental data and J-C modified model predictions

式中：下标exp 和mod 分别表示实验和J-C 本构模型预测值，N为实验数据个数。把实验数据和J-C 本构模型预测数据代入式(13)和式(14)，可求得R和δ。经计算，5 000 s-1、不同温度条件下的δ 在44%以内，R在0.72～0.95 之间。

J-C 本构模型仅通过应变硬化项、应变率强化项、温度软化项相乘将应变硬化、应变率强化和温度软化效应耦合，且确定每一项时，假定应变硬化项、应变率强化项和温度软化项彼此独立，并没有考虑应变、应变率、温度之间的耦合作用，无法描述应变硬化率随应变率的增大保持不变或降低的现象[19]。此外，材料的准静态变形过程可视为等温过程，而高应变率变形过程为绝热过程，J-C 本构模型没有考虑冲击变形过程的绝热温升影响，致使其对温度效应的预测结果低于实验结果[8]。

针对J-C 本构模型预测Ti6Al4V 在高温高应变率加载下的动力学响应存在的不足，对J-C 本构模型的形式进行修正，以描述应变率和温度对Ti6Al4V 动态屈服强度、应变硬化行为的影响，同时引入绝热温升软化项，以表达高应变率下绝热温升对应变硬化行为的影响[20]。修正的J-C 本构模型可表示为

式中：λ 为绝热软化系数，C1和C2分别表征应变率对初始屈服应力和应变硬化行为的影响，m1和m2分别表征温度对初始屈服应力和应变硬化行为的影响。Ti6Al4V 的修正J-C 本构模型参数采用如下方式确定。

假设等效塑性应变为零，则式(15)转化为

通过拟合应力-应变曲线在不同应变率和应变下的流动应力，得到A、C1、m1。m1随温度升高呈线性增长，可表示为

本构参数B、n、C2、m2的拟合是基于材料等温应力-应变关系得到的。首先计算绝热温升引起的应力变化Δσf

去除Ti6Al4V 冲击压缩动态真实应力-应变曲线中由绝热温升引起的应力变化，可得到等温条件下的修正应力-应变曲线。图11 显示了采用该方法得到的100 ℃、7 000 s-1条件下的绝热曲线和等温曲线。

图11 100 ℃、7 000 s-1 条件下等温曲线与绝热曲线的对比Fig.11 Comparison of isothermal curve and adiabatic curve at 100 ℃ and 7 000 s-1

对于材料的等温变形过程，式(15)可以转化为

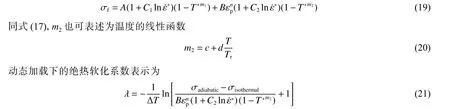
式中：σadiabatic和σisothermal分别为高应变率加载下绝热变形和等温变形过程对应的流动应力。修正J-C 本构模型参数列于表1。

表1 修正J-C 本构模型参数的拟合结果Table 1 Results of parameter fitting of modified J-C constitutive model

J-C 本构修正模型的预测结果与实验数据的对比如图12 所示。修正模型的预测精度良好，预测结果的R和δ 如图13 和图14 所示。所有工况下的R均大于0.85，δ 均在11.5% 以内，表明所构建的Ti6Al4V 的修正J-C 本构模型可以有效预测和表征材料在加载温度为100～800 ℃、应变率为2 000～7 000 s-1条件下的动态力学响应。

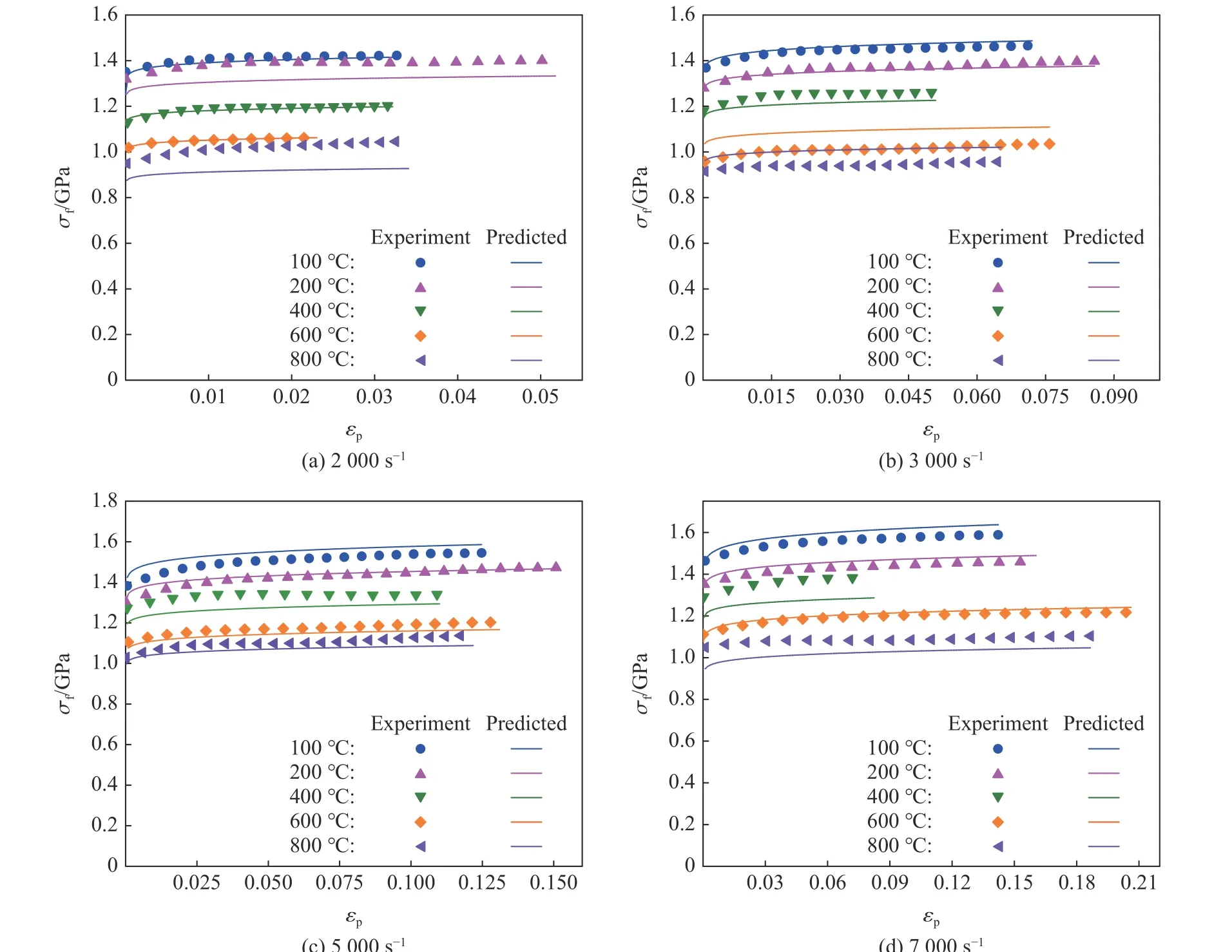
图12 Ti6Al4V 在不同加载条件下的实验数据与模型预测对比Fig.12 Comparison of experimental data and model prediction results of Ti6Al4V under different loading conditions

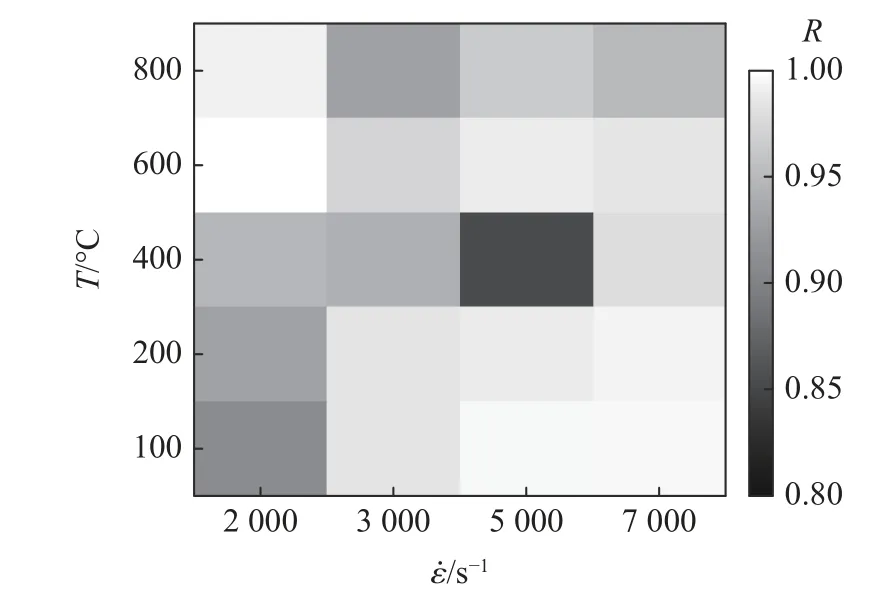
图13 不同加载条件下修正模型与实验数据的相关度Fig.13 Correlation degree between the modified model and experimental data under different loading conditions

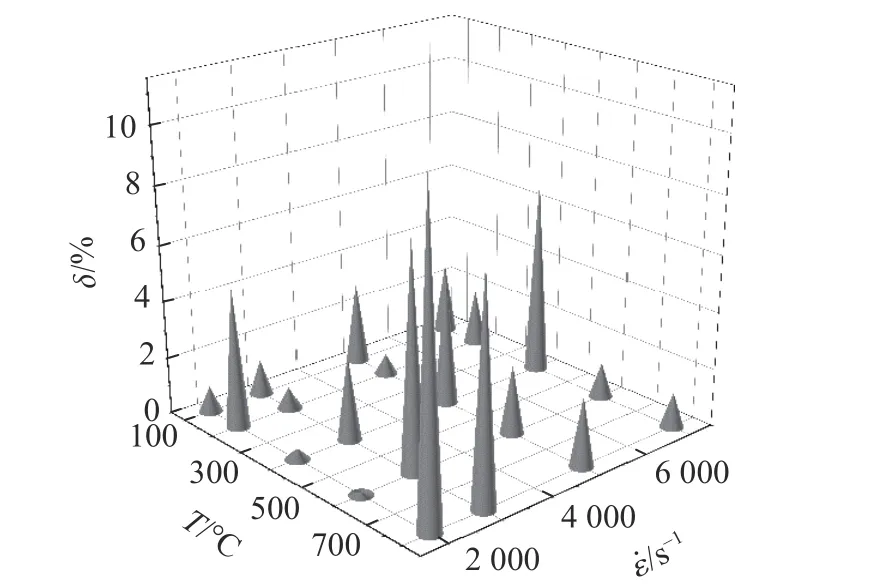
图14 不同加载条件下修正模型的平均相对误差Fig.14 Average relative error of the modified model under different loading conditions

4 结 论

(1) 率-热耦合加载下Ti6Al4V 呈现出显著的应变硬化、应变率强化、应变率增塑和温度软化效应。随着加载温度和应变率的升高，材料的应变硬化效应减弱。温度敏感性随着应变率的升高而增大，随着加载温度的升高而显著降低。应变率敏感性因子与加载温度呈负相关，但随真实应变的增加呈下降趋势。

(2) 高温高应变率下Ti6Al4V 的α 相沿加载轴向呈现出不同程度的压缩变形，形成拉长型α 相。当加载温度超过600 ℃时，在加载温度与绝热温升的耦合作用下，Ti6Al4V 再结晶产生新的等轴状α 相。回复过程中，α 晶粒开始长大。随着应变的增大，部分α 相在应变能的作用下成组合并，形成了直径大于50 μm 的块状α 相。高温高应变率下，细小等轴α 相、拉长型α 相和块状α 相取代初始等轴α 相成为Ti6Al4V 微观组织的典型特征。

(3) 针对J-C 本构模型预测Ti6Al4V 在高温高应变率加载下的动力学响应存在的不足，对J-C 本构模型的形式进行修正，以描述应变率和温度对Ti6Al4V 动态屈服强度、应变硬化行为的影响，同时引入绝热温升软化项，以反映高应变率下绝热温升对应变硬化行为的影响。修正J-C 模型的预测结果与实验结果的相关性系数大于0.85，平均相对误差小于11.5%，表明所构建的Ti6Al4V 的修正J-C 本构模型可有效预测材料在加载温度为100～800 ℃和应变率为2 000～7 000 s-1条件下的动态力学响应。