Prediction of Synthesis Condition and Magnetic Property of Screened Metallic Double-Perovskite Antiferromagnet Mn2FeOsO6

LI Jun, JIN Shangjian, ZHAO Shuang, YAO Daoxin, LI Manrong,4

（1.Key Laboratory for Microstructural Material Physics of Hebei Province, School of Science,Yanshan University, Qinhuangdao 066004, Hebei, China;2.State Key Laboratory of Optoelectronic Materials and Technologies, School of Physics,Sun Yat-sen University, Guangzhou 510275, Guangdong, China;3.Key Laboratory of Bioinorganic and Synthetic Chemistry of Ministry of Education, School of Chemistry,Sun Yat-sen University, Guangzhou 510275, Guangdong, China;4.School of Science, Hainan University, Haikou 570228, Hainan, China）

Abstract: We present a theoretical approach for predicting the electron configuration, polymorph,synthesis condition, and physical properties of complex magnetic double perovskite compounds.Our method is reasonable and computationally efficient, allowing us to identify an antiferromagnetic (AFM) metallic material, namely Mn2FeOsO6, with a high AFM Néel transition temperature (TN).Through extensive analysis, we demonstrate that Mn2FeOsO6 possesses a high density of states near the Fermi level and an AFM configuration, resulting in a zero total magnetic moment.Our findings suggest that the expected TN of Mn2FeOsO6 is as high as 680 K, representing a potential breakthrough in the field of spintronics.We have also constructed a sophisticated magnetic model for this material, and obtained a reasonably reliable magnetic excitation spectrum potentially comparable with neutron scattering spectra.This theoretical approach provides synthesis conditions that are consistent with many synthesized double perovskite compounds in experiments, and it holds promise for the prediction of other complex magnetic configurations.Our study may play a key role in the big data prediction of novel double perovskite materials.

Keywords: double-perovskite；antiferromagnet；Mn2FeOsO6

The field of antiferromagnetic (AFM) spintronics has recently garnered attention due to its ultrafast dynamics, zero net magnetization, and stability against external magnetic fields, which hold promise for future computing power[1-4].In these materials, information can be encoded by manipulating the antiferromagnetic order via domain wall motion[5], optical excitation[6], spin-orbit torques[3], and staggered local relativistic fields[7].Among the different categories of antiferromagnet, metallic antiferromagnet are particularly unique as they provide an ideal platform for fundamental studies and applications due to the strong interplay between electrons, spin,phonons, and photons[8-9].However, metallic antiferromagnets are rare, and the known materials display AFM order only well below room temperature (RT), which limits their practical applications.For instance, the transition-metal oxides Nb12O29[10], Ca3Ru2O7[11], CaCrO3[12], and LaNiO3[13]exhibit Néel transition temperatureTNof 12, 56, 90, and 157 K, respectively.Although RuO2exhibits AFM order at around RT (TN～ 300 K), the magnetic moment is as small as 0.05µB(µBrepresents Bohr magneton) at about 300 K.Therefore, exploring materials with RT magnetic order is of utmost importance for practical magnetic applications[1].

Recently, research on the magnetic properties of double-perovskite oxides A2BB'O6, where B and B'are ordered 3dand 4d/5dtransition metal ions, has demonstrated the emergence of homogeneous and long-range magnetic order due to periodic intrinsic magnetic ions and magnetic exchange interactions[2-9].These materials exhibit multiple functions resulting from multiple physical interactions, such as spin, orbit, dipole, and lattice.For example, such interactions give rise to magnetoelectric coupling based multiferroics[14-15], half-metallicity[16],colossal magnetoresistance[16], and ferromagnetic (FM) semiconductor and insulator[17]properties in RT perovskite-oxides magnets.

Theoretical analysis of A2BB'O6materials with divalent A-site alkali earth cations reveals that the maximum number of unpaired 3dand 4d/5delectrons can reach 3d5(in high spin) or 4d3/5d3() combination over the B- and B'-sites, such as in A2Fe3+B'5+O6(B'= Ru, Os) and A2Mn2+B'6+O6(B'= Rh, Ir) under charge balance.For example, the Ca2FeOsO6material exhibits electrically insulated behavior and undergoes a FM transition at about 320 K driven by lattice distortion and chemical pressure[6,18-19].In contrast, spin frustration arising from the disordered alignment of Fe3+/Ru5+in A2FeRuO6(Pbnmsymmetry)[20-21]may result in spin-glass or AFM behavior[22].Notably, the Fe/Ru ordered double perovskite Sr2FeRuO6is stabilized in film form by hetero-interface strain(chemical pressure) on SrTiO3substrate, achieving a Curie temperature (TC) of 390 K[23].To date, there are no reports on A2Mn2+Rh6+O6or A2Mn2+Ir6+O6.

The emerging research on exotic perovskites under high-pressure and high-temperature (HPHT) conditions has led to the investigation of transition metal cations at the A-site, resulting in enhanced magnetic interactions when compared to conventional analogs[14-15,17,24-34].The occupancy of the A-site by high-spind5-Mn2+cations can significantly increase the number of unpaired d electrons, thereby promoting strong magnetic interactions in Mn2BB'O6[35].Theoretically, there are 411 possible combinations of Mn2BB'O6in Mn2B1+B'7+O6, Mn2B2+B'6+O6,and Mn2B3+B'5+O6, as shown in Fig.1.Mn2B4+B'4+O6is unlikely to form ordered double perovskites and is ignored here.Up to now, only 20 compounds have been experimentally validated to crystallize in Mg3TeO6-type (R3)[36-37],Ni3TeO6-type (R3)[38-39], β-Li3VF6-type (C2/c)[40-42], and GdFeO3-type (P21/n)-type[43-44]structures, depending on the chemical and synthesis parameters (see Fig.1).

Taking the number of unpaired d electrons (nd), chemical valences and ionic radius into account, it is noteworthy that eight transition-metal-only (TMO) double perovskites withndbetween 14 and 18 exhibit robust magnetoelectric properties, which provides motivation for further exploration in this category.More than 70 TMO double perovskites can be formed in Mn2BB′O6by ordered combination of 3dand 4d/5dions over B- and B′-sites under charge balance, offering a vast space to explore new multifunctional materials.However, the normally arranged atoms will have a certain displacement and deformation due to the influence of strong magnetism[45],making TMO double perovskites’ symmetry further reduced than that of conventional nonmagnetic perovskites.As a result, tolerance factor (t)[46-47]and octahedral factor (µ)[48-49]as geometric descriptors for conventional perovskites with large A-cations are not longer suitable for the TMO double perovskites.Therefore, discovering these materials mainly relies on empirical intuition and costly trial-and-error in HPHT synthesis.

Recently, the successful prediction and precise synthesis of A3TeO6have provided insight into the screening of new materials oriented towards structure and function, which can help avoid the costly trial-and-error process involved in preparing magnetically exotic perovskites under HPHT[52-53].These studies have used first-principles density functional theory (DFT) calculations based on the Murnaghan equation of state for solids[54]to show that the phase stability between competing polymorphs can be estimated using the phase diagram of the relative enthalpy (ΔH), the total energy (E) and the pressure (p).The reported DFT-based workflow, which adopts a restricted collinear magnetic structure, has been shown to provide considerable accuracy in predicting the polymorph and corresponding synthesis parameters (such as pressure).However, for TMO double perovskites with 4d/5dions at the B′-site, the variation in the energy scale of possible interactions, such as magnetic interactions, spin-orbit coupling (SOC), Dzyaloshinskii-Moriya (DM) interaction, HubbardUand Hund’s interactions, cause a challenge for calculating these materials reliably and efficiently usingabinitiomany-body methods[45].This remains an open challenge in providing reliable and timely predictions for this strongly correlated perovskites family[55-56].Conversely, validation calculations based on experimentally reported TMO double perovskite-related compounds are expected to facilitate the understanding of dominant factors in inverse prediction and rational design.

In this article, we will firstly conduct test calculations on the known transition metal oxide Mn2BB'O6,establish calculation models, and then these models will be used to predict the pressure-dependent polymorph evolution and synthesis parameters of the TMO double perovskite Mn2FeOsO6, which contains a maximumndof 18.Additionally, we will propose several magnetoelectric properties of Mn2FeOsO6.Due to the high cationic disordering in corundum-type, Mn2FeRuO6is beyond the scope of this work, shown experimentally[25].

1 Symmetry Analysis

For double perovskite materials with the chemical formula A2BB'O6, the ideal crystal structure is usually doubled in all three crystallographic directions compared to a single perovskite ABO3, resulting in a space group ofFm3m[32].However, this only occurs when the size of the A-site cation is much larger than that of the B-site cation, i.e.with tolerance factortaround 1[57].When the size of the A-site cation is comparable to that of the B-site cation, i.e.with tolerance factortless than or equal to 0.85, the BO6octahedra will tilt to optimize the Acation bonding[58].According to Glazer’s tilt rule, there can be 12 tilt systems in A2BB'O6perovskites, as determined by Howardet al[59-60].As mentioned in our previous article[53], exotic double perovskites with transition metals andt≤0.85 may adopt one of six possible structures identified by database screening, including distorted GdFeO3-type double perovskite (P21/n), B-site ordered LiSbO3derivatives (Pnn2), Mg3TeO6(R3)[36-37],corundum derivatives (LiNbO3-typeR3c, ilmeniteR3, and ordered ilmenite or Ni3TeO6-typeR3)[38-39], bixbyite(Ia3), and β-Li3VF6(C2/c)[40-42].Based on chemical and geometrical considerations, the size and the charge differences between the A-site and B-site cations studied in this paper do not energetically favor the formation of bixbyite (Ia3) and LiSbO3derivatives (Pnn2).Therefore, we only consider the remaining four structures (R3,R3,C2/candP21/n).

Stretching the ideal face-centered cubic structureFm3malong the ＜111＞ direction results in theR3 structure, where the BO6octahedra tilts and the space group changes toa-a-a-in Glazer tilt systems.However, in practice, the orders of B and B'coordination can destroy the space-reversal symmetry, leading to theR3 polymorphs.The reportedR3cstructure is unlikely to happen for rock-salt double perovskite structures.

Meanwhile, theC2/candP21/nstructures can be obtained by sliding the idealFm3mstructure along the＜110＞ direction and considering the tilt of the BO6octahedra.In the case of small A-cations, the A cation is unlikely to maintain the ideal position, leading to the distortion of the lattice and the formation of theP21/nstructure witha+b-b-in Glazer tilt systems.BothC2/candP21/nconfigurations are commonly observed in double perovskite structures.

The single perovskite structure is also the most abundant inPnma(a+b-b-) andR3c(a0b-b-) configurations[48,61]since the tilt direction of BO6octahedra in the adjacent two layers of perovskite structure tends to be opposite.In the Glazer symbol, therefore, compared with in-phase BO6rotations, such asIm3 (a+a+a+) andPmmn(a-b+b+), the anti-phase BO6rotations are more common.When it comes to double perovskites A2BB'O6, two typical progress of octahedral tilts with decreasingthasbeenfoundas[62-63]

We note that in material calculations, A-site cations are always repelled or attracted by B-site cations due to the influence of magnetism and Jahn-Teller effect, making it difficult to maintain a square arrangement in a plane.Therefore, the common tetragonal lattice (I4/m(a0a0c-) orP4/mnc(a0a0c+)) in perovskite is hard to appear under the condition that both A- and B-sites of double-perovskite are transition metal ions.In fact, experimental research on this type of materials has also confirmed our conclusion, i.e.there is no report on tetragonal lattice doubleperovskite oxides with A-site alkali earth cations, B and B′ ordered transition metal ions so far, as shown in Fig.1(a).

In this work, we investigated the effect of magnetism on the lattice distortion of double perovskite structures,in addition to the BO6octahedral tilt induced by the small A-cation.Previous studies have also reported the influence of magnetism on the lattice distortion phenomenon[22-23,45].It is important to note that the nearestneighbor (NN) and next nearest-neighbor (NNN) interactions can have similar strengths.In the ideal double perovskite structure, there are many possible magnetic configurations.However, experimental observations have shown that only four magnetic configurations are mostly observed.There are three types of AFM order, namely,type-Ⅰ, type-Ⅱ, and type-Ⅲ, depending on the relative magnitudes of NN and NNN interactions.For type-Ⅰorder, the spins are anti-parallel between the [100] planes and parallel within the [100] plane.Type Ⅱ order occurs when the NN interactions are weaker than the NNN interactions, with the spins arranged anti-parallel between the[111] planes and parallel within the [111] plane.Type-Ⅲ order is an intermediate form in which the NN interactions are relatively strong, while the NNN interactions are still significant.

In addition to these four configurations, there are other disordered magnetic phases such as magnetic frustration and spin-glass-type behavior.However, these phases are less relevant to the present study, therefore,we limit our DFT calculation and analysis of structural optimization to the four aforementioned configurations.When analyzing the magnetic properties of materials, we consider as many magnetic configurations as possible to obtain more reliable magnetic properties.

Since most experimental synthesis of transition-metal double perovskites require HPHT conditions[64-66], we considered the synthesis pressure as a crucial parameter.To investigate the effect of pressure on the stability of double perovskite structures, we calculated the energies of all four lattice configurations and four magnetic configurations for each material under varying pressure conditions.

2 Model and Methods

To simulate the application of relatively large pressure, we started with a relatively small initial volume for each polymorph with a specific set of ingredients.We then gradually increased the simulating pressure by reducing the lattice to determine the most stable structure type at each given pressure.After that, we obtained the total energy (E) and volume (V) curve of each compound, and fit it with the Brich-Murnaghan function

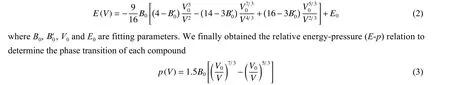
Our DFT calculations were performed using the Viennaab initiosimulation package (VASP)[67-70]with the projector augmented wave (PAW) method.We used the spin-polarized generalized gradient approximation (GGA)and the Perdew Burke-Ernzerhof (PBE) function to treat the electron exchange correlation potential[71].The plane wave kinetic energy cutoff was set to 400 eV.

To ensure our calculations are compatible with different magnetic configurations and atomic distortions, we used a 40-atom supercell, which can be considered as a (2, 2, 2) multiple of the ideal single perovskite structure along the three axes of Cartesian coordinate[50-51].The Γ point only in VASP was used to accelerate the crystal structure optimization until the force on each atom is less than 0.001 eV/Å.We built initial structure models for calculations by elemental substitutions of the crystallographic information files of known compounds with elemental substitutions.

To investigate the effect of pressure on the stability of double perovskite structures, we applied isotropic pressure during the calculations.In DFT calculations, we have considered various factors, such as collinear magnetic structure, SOC, DFT+U(UFe= 4.6 eV,UMn= 4 eV,UOs= 2.0 eV), and non-collinear magnetic structure to determine which factors would have undeniable impact on the structure.

For Mn2FeOsO6, its magnetic properties can be described by the Heisenberg Hamiltonian

where the symbolSi(Siz) represents the spin operator at the lattice sitei(along the z direction),Jijrefers to the Heisenberg exchange betweenSiandSj,Drefers to the DM interaction, and Δsrepresents the single-ion Ising anisotropy.

There are 8 magnetic atoms in a supercell, and it is needed to consider 64 types of magnetic exchange interactions between these magnetic ions.If we ignore magnetic exchange interactionJbetween identical magnetic ions (i.e.Jii= 0) and the directional dependence between different magnetic ions (i.e.Jij=Jji), there are 28 distinct values left.Therefore, we need to calculate these 28 different magnetic exchange interaction values individually.

We calculated 64 different magnetic configurations among the total 28= 256 configurations in the magnetic unit cell containing 8 magnetic ions.Because the magnetic anisotropy is basically negligible, we used collinear magnetic DFT calculations to save the resources requirement.These 64 magnetic configurations are enough to obtain 28 unknownJ.In order to simplify the calculation, we used the linear matrix method to calculateJone by one using the minimum dichotomy method

3 Validation Calculations on Known Two Double Perovskites

Table 1 provides the details of the synthesis conditions, structural symmetry, electron configurations, and physical properties of TMO double perovskites A2BB'O6where B- and B′-site cations is transition-metal atoms.The Re-based compounds crystallize in a distorted GdFeO3-type monoclinic structure (P21/n), while Mo-based and W-based compounds are more likely to adopt rhombohedral symmetry (R3).Previous studies have shown that DFT caculations in consideration of only collinear magnetic structures can yield reasonable and acceptable overall trends of synthesis condition andE-pphase diagrams for TMO double perovskites[52-53].

Table 1 Structural and electronic properties of the 7 experimentally realized TMO double perovskite-related compounds,along with the predicted Mn2FeOsO6.Here nd≥14 provide certain displacement and deformation due to the influence of strong magnetism, resulting in low symmetry (R3 and P21/n)

We investigated the effect of other possible properties, such as DFT+U(UFe= 4.6 eV,UMn= 4 eV,UOs=2.0 eV), and the role of non-collinear magnetic structure, on the energy-volume (E-V) results, but found that these interactions do not impact the results significantly.Therefore, we concluded that these additional interactions could be ignored in structural optimization, and we only adopted collinear magnetic structures in the structural optimization calculations to save computational resources.

To be clear, we started with Mn2MnReO6with the knownP21/nstructure synthesized in previous studies[16,29-30].To evaluate the effect of magnetism on the crystal structure, we calculated theE-Vcurve using the Brich-Murnaghan function.It turns out that for collinear magnetic structures, the magnetism contribution to the energy difference is on the order of 0.1 eV/atom, accordingly, having an effect on the lattice structure.However, theE-pcurve calculated using Eq.(3) shows that, theR3 structure is the most stable one whenp≤10 GPa, with a minimum energy difference of less than 0.1 eV per cell without considering the magnetic structure.This small energy difference results in inconsistency between the calculatedR3 output and the experimentalP21/nresult.Therefore, we must consider the magnetic structure in TMO double perovskites.We conjectured that the magnetic exchange between magnetic ions in Mn2MnReO6would affect the crystal structure, and the magnetic contribution of atoms should be considered in the DFT calculations of structure optimization.After considering magnetic structure, the type-Ⅱ AFM configuration has the lowest energy of the four collinear magnetic structures considered, which is a good validation of previous experiment results[29-31].

In the present study, we investigated the polymorphic phase transitions of five double perovskite compounds,namely Mn2MnReO6, Mn2CoReO6, Mn2FeReO6, Mn2FeMoO6, and Mn2FeWO6.In our calculations, we have considered the four different magnetic configurations and obtained their respectiveE-Vrelations (see Fig.2(a)-Fig.2(e)).However, due to the existence of metastable magnetic structures, the total magnetic moment after DFT convergence is found to be inconsistent with the calculations of a single magnetic configuration.TheE-Vcurves also exhibit abnormal points and protrusions, rendering the fitting of these curves with the Brich-Murnaghan function inaccurate.To address this issue, we selected the magnetic structure with the lowest energy under eachVpoint of the four magnetic configurations as the source ofE-Vcurve.By uniformly fitting theseE-Vcurves with the lowest energy, we obtained appropriate parameters to produce a sufficiently reliableE-pcurve.

Fig.2 E-p curves of Mn2FeWO6 and Mn2FeMoO6, as well as Mn2FeOsO6 with the magnetic structures in Table 1.(All these results are fitted by Brich-Murnaghan function Eq.(3) in consideration of the lowest energy of four collinear magnetic configurations.)

Upon adding magnetism, we observed that although the influence of magnetism on each structure is different, the total energy of the system is reduced by about 1 eV per cell.For Mn2MnReO6, such a small influence of magnetic exchange energy is able to reverse the two energy levels ofR3 andP21/nstructures under the external pressure around 7 GPa, beyond which theP21/nstructure is more stable and in good agreement with the experimental results[29,31].Notably, 5 GPa is needed to prepareP21/nMn2MnReO6in the experiment[29], and the gap of 2 GPa between theory and experiment may be caused by the 1 400 ℃ treatment and can be considered as within the theoretical error range.

We then applied this method to the related double perovskite compounds that had been experimentally prepared.In our calculations, the lowest synthesis energy configuration of Mn2CoReO6is always theP21/nstructure, which roughly echoes the experimental results[26].For Mn2FeReO6, the synthesis energies of the four structures exhibit little differences in the pressure range considered.The energy ofR3 overlaps that ofP21/nat 5 GPa, being consistent with the synthetic conditions in the experiment[16].The situations of Mn2FeMoO6and Mn2FeWO6are similar.Both compounds show theR3 structure under high pressure, and the synthesis conditions are about 6 GPa.We also checked the calculations without considering magnetic conditions and found that they do not match experiments.Validation calculations on these five synthesized double perovskite materials prove that our proposed method for computing polymorph-dependent phase diagrams is reliable.

4 Magnetism of Mn2FeOsO6

In this section, we present predictions on the structure and the properties of Mn2FeOsO6, a compound that has not yet been experimentally synthesized.Our DFT calculations demonstrate that theC2/cstructure is relatively stable under atmospheric pressure, as illustrated in Fig.2(f).However, under a pressure greater than 5 GPa, theP21/nstructure with type-Ⅲ AFM configuration becomes the most stable.

In addition, our calculations on the possible magnetic structures of Mn2FeOsO6revealed a standard AFM configuration, where the magnetism of each magnetic ion is reversed.Specifically, in a 40-atom supercell, four spins of the eight Mn atoms are opposite to the other four, and two spins of the four Fe atoms are also opposite to the other two.We have also confirmed that the magnetic anisotropy is relatively small, as the energy difference per cell caused by magnetism in the lattice vectorsa,b, andc(Fig.3(a)) directions is less than 0.1 meV.

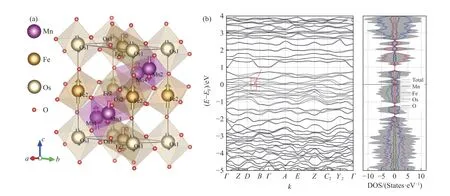
Fig.3 DFT results of Mn2FeOsO6 in consideration of SOC, DFT+U (UFe = 4.6 eV, UMn = 4 eV, UOs = 2.0 eV) and non-collinear magnetism: (a) the predicted atomic and magnetic structures, with a distorted GdFeO3-type monoclinic structure (P21/n) as for Mn2FeReO6[16,29-30] (The arrow on each atom represents the spin orientation and the size of spin value.Every spin is almost laying at ＜001＞ direction, forming a relatively ideal AFM configuration.); (b) energy band structure near Fermi level and spin-resolved density of states (DOS) (Mn2FeOsO6 has no bandgap, forming as conductor.There is a suspected formation of Dirac points between wavevectors B-D, marked by red rectangle and arrow.The DOS of spin-up and spin-down are basically the same, verifying the AFM configuration of Mn2FeOsO6.)

We then proceeded to approximate the magnetic properties of Mn2FeOsO6.Our calculations showed that the total magnetic anisotropy energy (MAE) in a single magnetic unit cell is negligible ( Δs＜0.1 meV) in consideration of SOC, and the spins of magnetic atoms exhibit almost collinear configuration with only a degree difference of less than 5°, as depicted in Fig.3(a).Therefore, in the estimation of magnetic properties, we neglected the MAE,as well as DM interaction, and only considered Heisenberg exchange in Eq.(4).

As illustrated in Fig.3, Mn2FeOsO6contains 8 magnetic ions in a single magnetic unit cell.Among them, the four Mn ions possess a local magnetic moment of approximately 4.5µB, and the two Fe ions possess a local magnetic moment of approximately 4µB, while the two Os ions possess a local magnetic moment of approximately 1µB.Although basically Os ions is not magnetic, they exhibit magnetism induced by the surrounding strong magnetic Mn and Fe ions.

In our magnetic exchange model for Mn2FeOsO6, we calculated 28 differentJdue to the irregular configuration of the magnetic ions in theP21/nstructure.Here, we present a few examples to illustrate the numerical values of theseJ.The AFM exchanges (J＞ 0) between the NN Mn ions (J13≈J24) and NNN ones are approximately equal to the values reported in [74].However, due to the low symmetry ofP21/n, there are two different distances between NN Mn ions, resulting in slightly different FM exchanges (J23＜J14) induced by indirect Ruderman-Kittel-Kasuya-Yosida (RKKY) exchanges.Thus, our group of magnetic exchange models, which contains 8 different magnetic ions, is considered to be reliable.

According to the aforementioned magnetic structure model, we constructed the corresponding exchange interactions between magnetic ions, as shown in Table 2.The result of spin dynamic behaviours of Mn2FeOsO6is shown in Fig.4(b).Note that we have ignored the DM interaction and single-ion Ising MAE in the Hamiltonian.An obvious value of intensity is shown at AFM order wave vectorQAFM= (0, 0, 1).As the NN interactions are on the order of 10 meV, the maximum of the magnon dispersion reaches 600 meV.Interestingly, the 8 bands along theZ-Dmomentum path all show characteristics of flat band.

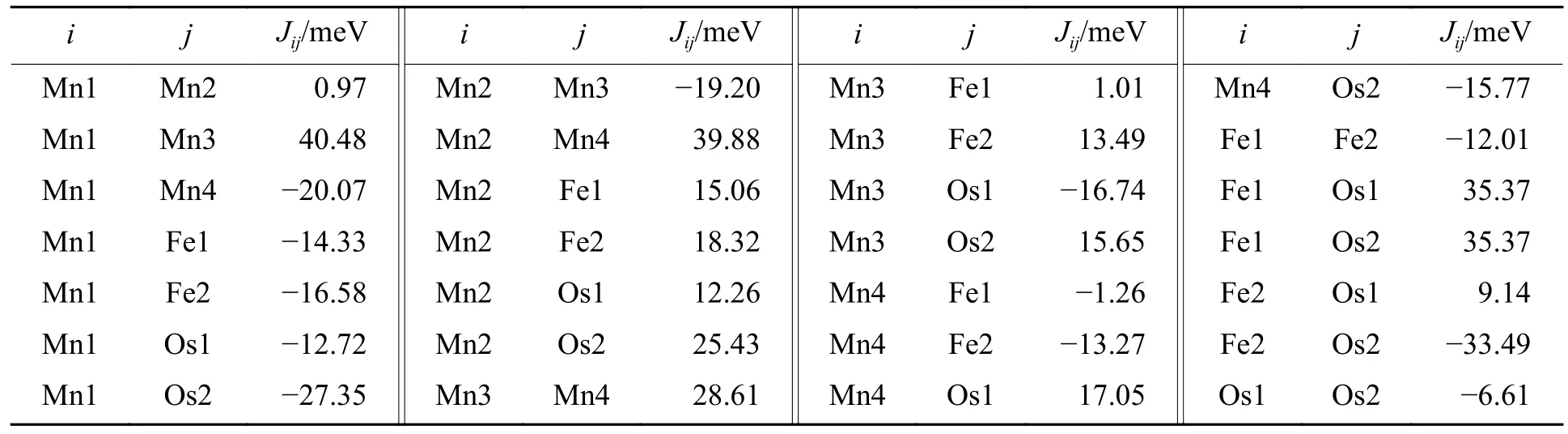
Table 2 Magnetic exchange Jij between magnetic ions within a magnetic unit cell of Mn2FeOsO6

In Fig.4(a), the magnetization and magnetic susceptibility of Mn2FeOsO6were calculated using classical Monte Carlo simulations with Metropolis algorithm.It was observed that the magnetic susceptibility curve has two peaks, indicating the possible existence of two different AFMTNin this system, consistent with previous experiments[29].We propose that this phenomenon is due to two sets of AFM atoms at A and B sub-lattices.The higher AFMTNis directly dependent on the Mn ion at A-sites.The estimatedTNis above 680 K, which is higher than theTN(orTC) observed in related experiments.It is noteworthy that the estimated transition temperature is relatively conservative.The actual transition temperature would be further increased if the MAE resulting from shape and DM interaction is considered.

Additionally, the electronic band structure of Mn2FeOsO6was computed, shown in Fig.3(b).Due to the low lattice symmetry, the energy bands are complex and disordered.However, in contrast to other TMO double perovskites, Mn2FeOsO6exhibits metallic properties, with a high DOS near the Fermi surface.The DOS indicates that the energy band near the Fermi level is primarily contributed by the 3delectrons of the magnetic ions.Furthermore, the system presents an AFM configuration, where the spin up and down DOS are consistent, and the total magnetization equals zero.Thus, Mn2FeOsO6is an ideal AFM metallic material.

Finally, the excitation spectrum mode of the above spin model was computed using the spin-wave method.The excitation mode, shown in Fig.4(b), reveal clear AFM imprints in the ＜100＞ direction, consisting of two sets of different AFM excitation spectra, supporting the previously estimated AFM configuration obtained by our Monte Carlo method.

5 Conclusions

In conclusion, we extend a method that can determine the complex magnetism configuration and synthesis condition of double perovskite materials at the same time consuming relatively low computational resources.Our method is shown to provide satisfactory results for several known double perovskite compounds.

We apply this method to investigate the promising material Mn2FeOsO6, which has not yet been experimentally synthesized.Our analysis reveals that this material has aP21/nstructural configuration with a high density of states near the Fermi level, making it an ideal AFM metal with a total magnetic moment of zero.Using a set of matrix operations, we are able to obtain the complex magnetic exchange interaction of theP21/nstructure,and identify two sets of AFMTN.Our findings are further verified by classical Monte Carlo simulations and spin wave excitation spectrum analysis.

Overall, we theoretically identify an ideal AFM metal with extremely high AFMTN, which has promising applications in the field of spintronics.Our method is an effective approach to study complex magnetism in double perovskite materials and can be extended to investigate other related materials.