束状孔与当量大孔爆破应力波在节理岩体中的衰减规律
2024-02-23熊常然
熊常然 陈 何
(1.北京矿冶研究总院,北京 100160;2.矿冶科技集团有限公司,北京 100160)

由于岩体是由节理和裂隙以及被他们分割成的岩石所组成的复杂地质体,而节理的存在会使爆炸应力波在结构面处发生反射、折射和透射,同时会导致炸药爆破的能量从结构面“泄出”,严重阻碍爆炸应力波的传播[2],最终导致爆炸产生的能量分布不均,使得炸药能量利用率低,影响爆破作用效果。关于普通单孔爆炸应力波在节理岩体中的传播规律,国内外学者已经进行了不同方面的研究[3-6],然而针对束状孔爆破在节理岩体中爆炸应力波传播规律的研究较少,为了更加具体地了解节理对束状孔爆炸应力波传播规律的影响以及节理岩体中束状孔与当量大孔爆破的区别,本文通过构筑不同节理厚度的束状孔与当量大孔混凝土模型进行爆破试验。
1 模型试验
1.1 模型设计
以某矿山的工程岩体为原型,主要研究不同布孔方式下,节理岩体中爆炸应力波的传播规律,因此主要考虑试验模型材料力学性质的相似关系[7,8]。基于模型试验的精度和工作量,将相似比取为4。模型选用42.5R普通硅酸盐水泥,粗骨料为石子,最大粒径不大于2 cm,河砂的粒径小于1 mm,水泥∶石子∶河砂∶水为1∶1.69∶1.21∶0.4(质量比)。
在浇注混凝土模型时,在同一批次混凝土中制作标准模型进行普通混凝土抗压强度试验、静力受压弹性模量试验和劈裂抗拉强度试验,对模型材料的静力学性能进行测定,得到的模型材料力学参数见表1。

表1 岩体与模型材料物理力学参数
节理岩体模型爆破试验共制作4个直径2.4 m、高度0.6 m的混凝土圆柱体模型,其中束状孔与当量大孔模型各2个。为了避免爆生气体的影响,束状孔模型中炮孔用4根直径30 mm的钢管垂直布置在模型中心,束内孔间距为120 mm(图1);当量大孔模型炮孔为1根直径60 mm的钢管垂直布置在模型中心(图2);每个模型分别在4个方向布置不同厚度(4~16 mm)的节理,节理材料选用PVC板进行模拟,垂直布置在各个模型中,为减少不同方向上的应力波之间互相干扰,节理材料长度不宜过大,节理材料长度选取为300 mm。

图1 不同节理厚度的束状孔模型(单位:mm)Fig.1 Bunch-holes models with different thicknesses of joints(Unit:mm)
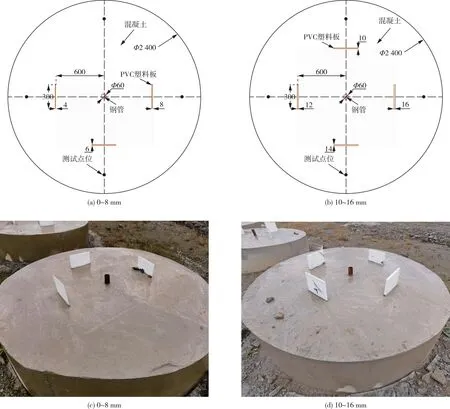
图2 不同节理厚度的当量大孔模型(单位:mm)Fig.2 Equivalent large hole models with different thicknesses of joints(Unit:mm)
1.2 试验方法
为了研究束状孔和当量大孔在不同节理条件下的爆破应力波传播规律,采用混凝土制作节理岩体相似模型,采用PVC塑料板模拟充填节理,每个炮孔由钢管包围,忽略爆生气体的作用,以导爆索束作为炸药对束状孔与当量大孔的混凝土节理模型进行爆破,采用TC-4850N测振仪监测爆炸应力波的振动速度。
炸药选用PB12型导爆索,用小刀切段(5 cm/段)并由胶带绑成一束(图3),由数码电子雷管起爆。装药量为9.2 g,埋藏深度(以药包中心计算)为11.5 cm。测振仪布置在每个节理后远离炮孔的方向,起爆后多台测振仪同时采集信号。

图3 导爆索束Fig.3 Manufacture of the detonating cord bundles
2 试验结果与讨论
2.1 试验结果
束状孔模型和当量大孔模型的测振仪采集的数据分别见表2、表3。将测点的三个方向速度曲线进行合成,得到不同节理厚度的束状孔模型合成速度时程曲线分别如图4、图5所示。
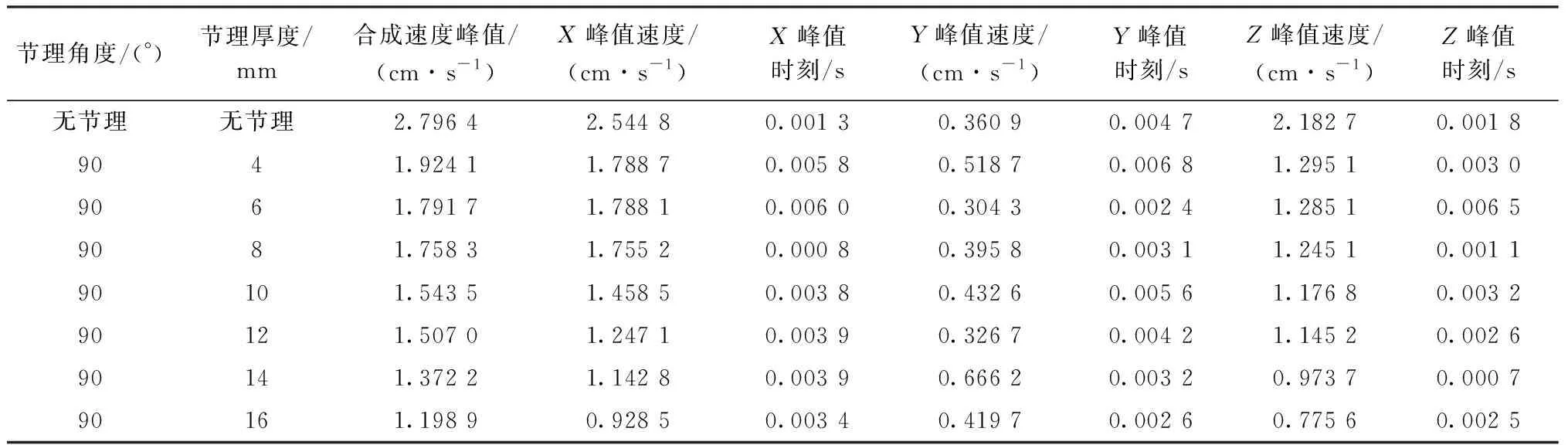
表2 束状孔模型数据
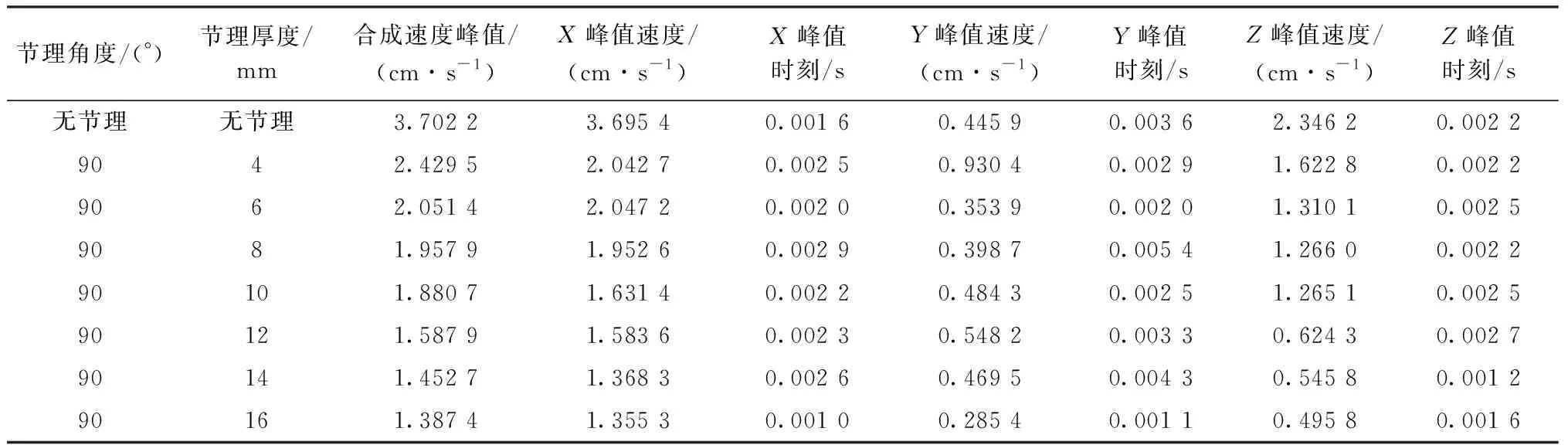
表3 当量大孔模型数据

图4 束状孔模型不同节理厚度合成速度时程曲线Fig.4 The vector velocity-time curves of bunch-holes models under different thicknesses of joints

图5 当量大孔模型不同节理厚度合成速度时程曲线Fig.5 The vector velocity-time curves of equivalent large hole models under different thicknesses of joints
2.2 结果分析与讨论
2.2.1 节理厚度对爆炸应力波的影响
对比图4和图5可以看出,爆炸应力波经过节理后会呈现出多峰状态,说明爆炸应力波在经过节理时会在节理内发生多次反射和折射;随着节理宽度的增加,节理对爆炸应力波的阻碍作用也变大,并且应力波峰值到达时间逐渐延长,即应力波在节理内的传播时间与节理厚度成正比。由此可以判断,节理的存在对爆炸应力波有明显的泄能作用,炸药爆炸的能量会以“冲炮”或者其它形式从节理中泄出,从而导致爆破作用效果降低。
不同节理厚度的束状孔与当量大孔模型峰值速度曲线如图6所示,衰减系数对比数据见表4。从图6可以看出,两种布孔方式的测点峰值速度均是随着节理厚度增加逐渐减小;当节理条件从无节理到节理厚度为4 mm时,测点峰值速度都急速下降;当节理厚度为4~16 mm时,峰值速度开始呈线性缓慢降低,节理厚度对于两种布孔方式爆炸应力波的影响规律总体上相似:随着节理厚度的增加,应力波峰值到达时间逐渐延长,测点峰值速度逐渐降低。

表4 不同节理厚度衰减系数数据

图6 不同节理厚度峰值速度对比Fig.6 Comparison of peak velocities under different thicknesses of joints
由表4可知,在相同的节理厚度条件下,束状孔与当量大孔爆炸应力波衰减系数在节理厚度为4 mm时分别约为31.19%和34.38%,在节理厚度为16 mm时分别约为57.1%和62.5%;束状孔爆炸应力波的衰减系数均小于当量大孔爆炸应力波的衰减系数,相差幅度在3.19%~11.00%。
为了进一步研究节理厚度对束状孔和当量大孔的影响区别,采用Origin软件对数据进行拟合,结果如图7所示。
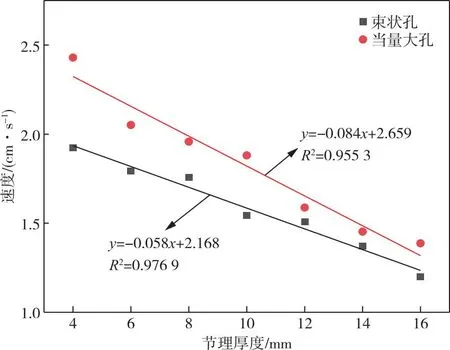
图7 峰值速度与节理厚度关系拟合曲线Fig.7 Fitting curves of the relationship between peak velocity and joint thickness
图7中,x—节理厚度L,mm;y—测点节理模型测点峰值速度v,cm/s。得到的衰减公式分别见式1、式2。
束状孔:v=-0.058L+2.168
(1)
当量大孔:v=-0.084L+2.659
(2)
从图7可以看出,当量大孔模型拟合曲线的截距大于束状孔模型的,差值约0.491,说明当量大孔的爆炸应力波峰值远高于束状孔模型,这也对应了当量大孔爆炸应力波高峰值的特点;束状孔模型拟合曲线的斜率绝对值小于当量大孔模型,差值约0.025,即束状孔模型测点峰值速度v1随着节理厚度L的增加而衰减的幅度小于当量大孔模型的衰减幅度。原因主要是束状孔中多个炮孔的爆炸应力波在节理处产生的多个反射波和透射波相互叠加,应力波在节理内反射的次数越多,该节理对应力波传递的影响就越小。因此,岩体中相同厚度的节理对束状孔爆炸应力波的衰减作用比当量大孔的更小。
2.2.2 束状孔与当量大孔的爆炸应力波波形比较
对比图4(a)和图5(a)可以看出,束状孔爆炸产生的爆炸应力波呈多个波峰形态,而当量大孔爆炸产生的爆炸应力波则呈现单峰形态,并且峰值更大,但应力波峰值过高可能会使炮孔周围出现较大的粉碎区,相对而言,束状孔爆破可减少出现较大的粉碎区。假定炸药在爆炸后产生的爆炸应力波能起到破岩效果的合成速度需大于1 cm/s,即为图4(a)和图5(a)内显示的有效作用区间,那么束状孔的有效作用区间长度要大于当量大孔的有效作用区间长度,即束状孔爆炸应力波的作用时间更长,炸药能量利用率更高。
综上可知,与当量大孔爆炸相比,束状孔爆炸更具优势。
3 结论
1)节理的存在会影响束状孔爆炸应力波的传播。
2)随着节理厚度的增加,节理厚度对应力波衰减的影响会逐渐变大,不同节理厚度下的束状孔爆炸应力波的衰减率更低。
3)在节理岩体中,束状孔爆破的应力波作用时间比当量大孔的更长,对炸药的能量利用率更高,同时束状孔爆破能够尽可能减少出现岩石过粉碎现象,从而改善爆破作用效果。
