钢筋混凝土黏结⁃滑移行为敏感性分析及机器学习模型

李宏伟，王文武，贾冯睿，苏昱太，龙旭

钢筋混凝土黏结⁃滑移行为敏感性分析及机器学习模型

李宏伟1，王文武1，贾冯睿2，苏昱太3，龙旭3

（1.辽宁石油化工大学 土木工程学院，辽宁 抚顺 113001； 2.浙江清华长三角研究院，浙江 嘉兴 314006；3.西北工业大学力学与土木建筑学院，陕西 西安 710072）

针对钢筋混凝土黏结⁃滑移行为，利用ABAQUS有限元软件，构建了基于内聚力模型的钢筋混凝土黏结⁃滑移有限元模型，通过能量和荷载⁃位移曲线探究了仿真模型网格敏感性以及内聚力参数敏感性。针对钢筋混凝土黏结强度问题，建立基于非线性自回归动态神经网络模型（NARX）的预测模型，以黏结长度、钢筋直径和加载方式为变量，建立20组数据对钢筋的荷载⁃位移曲线进行了预测。结果表明，当网格尺寸为6 mm时，可以较理想地平衡预测精度与计算成本；有限元预测结果对内聚力参数的敏感性由强到弱依次为损伤起始强度、断裂能和刚度；所建立的NARX预测精度达到99.6%，有潜力代替量大且耗时的数值模拟和物理试验，实现对钢筋混凝土黏结强度的高效准确预测，为钢筋混凝土黏结强度的预测和设计提供新的便捷途径。

钢筋混凝土黏结⁃滑移行为； 内聚力参数； 网格尺寸； 敏感性分析； NARX

钢筋混凝土具有承载力大、抗变形能力强、价格低和抗震等优势，被广泛应用于石油化工与天然气工程，而钢筋混凝土结构在油气管道支护方面具有重要的作用[1]。马国锐等[2]采用ANSYS软件，对钢筋混凝土管道结构进行数值模拟，解决了工程试验难以测得钢筋混凝土管道内部钢筋应力的难题。刘伟等[3]对油气管道中钢筋混凝土框架结构进行了调研。结果表明，采用装配式螺栓连接方式可以提高钢筋混凝土的结构稳定性。钢筋混凝土结构之所以能保持稳定，原因在于钢筋混凝土之间具有良好的黏结性能[4]。针对钢筋混凝土黏结⁃滑移问题，近年来国内外学者开展了一系列基于有限元仿真的数值研究工作。X.L.WANG等[5]建立钢筋混凝土结构模型，探究了混凝土保护层厚度对钢筋与混凝土之间黏结⁃滑动行为的影响。Z.Y.SUN等[6]以五根不同类型的钢筋加固的混凝土梁为研究对象，提出了基于等效黏结面积概念的简化黏结⁃滑移模型。A.ROLLAND等[7]建立纤维增强聚合物（FRP）钢筋混凝土的局部黏结⁃滑移模型，探究了钢筋混凝土之间的黏结性能。Z.H.WANG等[8]和郑山锁等[9]建立考虑冻融损伤的黏结⁃滑移模型，以混凝土材料强度和保护层厚度为条件，研究了钢筋混凝土之间的黏结性能。F.M.MUKHTAR等[10]采用两种不同的双剪切搭接试验设备，研究了纤维增强聚合物与混凝土之间的黏结性能。吴业飞等[11]以FRP钢筋混凝土为研究对象，进行分析并拟合内聚力参数，计算得到了断裂能和黏结强度，准确地得到了试件的极限承载力。J.HE等[12]研究了用韧性黏合剂黏合的FRP⁃钢接头的黏合行为，提出了一个有效黏结长度的模型。谢浩等[13]建立三维圆柱体板岩单轴压缩模型，从力学性能和破坏形态角度讨论了网格敏感性以及内聚力参数对模型预测结果的影响。牟晓光[14]通过二维钢筋混凝土黏结⁃滑移有限元模型，探究了钢筋的外形对混凝土黏结性能的影响。V.RANKOVIC等[15]建立支持向量机非线性自回归模型，对静水压力和温度作用下混凝土大坝的切向位移进行了预测，并对预测结果与物理实验结果进行了对比。结果表明，通过支持向量机非线性自回归模型可以得到较为准确的结果。O.B.OLALUSI等[16]基于高斯过程回归和随机森林技术，预测了无箍筋钢纤维混凝土细长梁的极限抗剪能力。L.DAI等[17]利用多层感知器神经网络和机器学习算法，探究了混凝土的抗压性能。结果表明，多层感知器神经网络预测混凝土抗压强度精度高。

研究人员对内聚力本构模型的钢筋混凝土黏结⁃滑移模型进行了大量研究。但是，尚未系统研究网格尺寸和内聚力参数对基于三维有限元模型的钢筋混凝土黏结⁃滑移行为的影响。本文以钢筋混凝土黏结⁃滑移模型为研究对象，采用内聚力理论建立有限元模型，通过与试验曲线进行对比分析，验证了所提出的内聚力有限元模型及所采用参数的正确性。在经过验证的有限元模型的基础上，进一步研究了内聚力本构行为对网格尺寸和内聚力参数的敏感性，从能量和响应曲线的角度考虑了网格敏感性以及网格敏感性与内聚力参数之间的关系。通过数值模拟的方法，将黏结长度、钢筋直径和加载方式作为输入层，将钢筋的荷载作为输出层，建立预测钢筋混凝土黏结⁃滑移行为的机器学习模型，以期为数值研究钢筋混凝土内聚力行为提供一个可靠且快速的分析手段。

1 内聚力模型

内聚力的发展主要分为三个阶段，分别为弹性变形的牵引⁃分离阶段、损伤起始阶段和损伤演化阶段。六面体内聚力单元如图1所示，双线型内聚力本构模型的损伤演化响应图如图2所示。图2中，横坐标为损伤位移，纵坐标为损伤强度；0为损伤起始强度，对应点的纵坐标；0、1分别为损伤起始点和损伤失效点所对应的位移，分别对应点和点；为弹性阶段的刚度，对应线段的斜率；为整个损伤阶段产生的能量，对应三角形的面积；为损伤变量，（1-）代表内聚力单元刚度的折减，对应线段的斜率。

图1 六面体内聚力单元

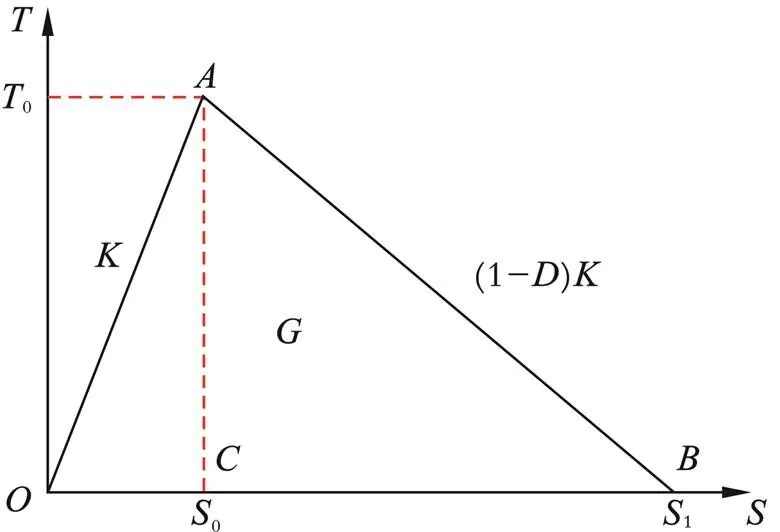
图2 双线型内聚力本构模型的损伤演化响应图

由图1及图2可以看出，当内聚力单元中应力满足损伤起始准则时，相邻的两个单元之间开始开裂并进入损伤演化阶段。随着两个单元的位移逐渐增加，内聚力单元应力逐渐降低，当达到一定位移时，单元间的内聚力彻底消失，裂纹的扩展也随之终止。

1.1 牵引⁃分离阶段

牵引⁃分离定律（Tension⁃Separation Law）用于描述图2中段的内聚力单元的弹性变形，其主要目的是建立牵引力与单元分离度之间的内在联系。当一个内聚力单元分离度达到一个特定材料的损伤起始位移0时，材料之间的黏结力开始减弱。牵引⁃分离定律的本构关系通常定义为：

式中：n为法向应力分量，MPa；s为第一切向应力，MPa；t为第二切向应力，MPa；为内聚力单元应力矢量，MPa，由n、s和t组成；nn、ns、nt分别为法向刚度、第一法向刚度、第二法向刚度，TN/m；ss、tt、st分别为切向刚度、第一切向刚度、第二切向刚度，TN/m；为内聚力单元弹性刚度，TN/m，由nn、ss和tt组成；n为法向应变分量，‰；s为第一切向应变分量，‰；t为第二切向应变分量，‰；为内聚力单元应变矢量，‰，由n、s和t组成。

1.2 损伤起始阶段

损伤起始准则是描述材料开始表现损伤行为的判定依据，即图2中的点。为了更好地探究内聚力单元的应力关系，采用二次名义应力准则（Quadratic Nominal Stress Criterion）作为损伤起始的判断依据：

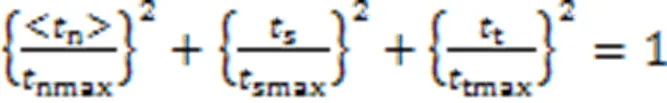
式中：nmaxsmax和tmax分别为法向、第一切向和第二切向内聚力单元所能承受的最大应力，MPa。

1.3 损伤演化阶段

损伤演化规律用于描述损伤起始后内聚力单元刚度退化的规律，即对应于图2中线段的斜率。该阶段通过引入损伤变量，描述内聚力单元刚度的退化过程。为了完整描述损伤演化阶段，在损伤起始并逐渐积累的过程中，损伤变量的取值从0单调地演化增加到1，从而判定材料的完全失效。为了更加合理地描述损伤演化过程，采用基于能量的损伤演化（Energy⁃Based Damage Evolution）模型，其表达式为：

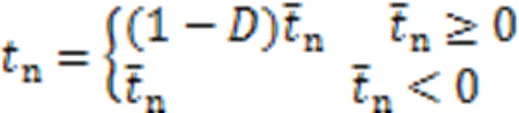
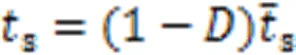
2 钢筋混凝土黏结⁃滑移行为的有限元模型

2.1 钢筋混凝土局部黏结⁃滑移性能测试方法

钢筋混凝土的黏结性能测试方法主要包括中心拉拔试验、梁式试验和局部黏结⁃滑移试验。其中，中心拉拔试验和梁式试验为典型的探究钢筋混凝土黏结性能的试验方法，但只能得出平均黏结应力，并不能很好地体现试件内部某一点的黏结应力与位移之间的关系。因此，通过局部黏结⁃滑移试验，获得钢筋混凝土局部黏结⁃滑移性能的试验数据。拉拔试件示意图如图3所示。钢筋混凝土的局部黏结⁃滑移试验能充分体现钢筋混凝土接触面间的力与位移的关系，而在钢筋混凝土结构分析的有限元模型中同样需要充分考虑钢筋与混凝土之间的相互作用规律。

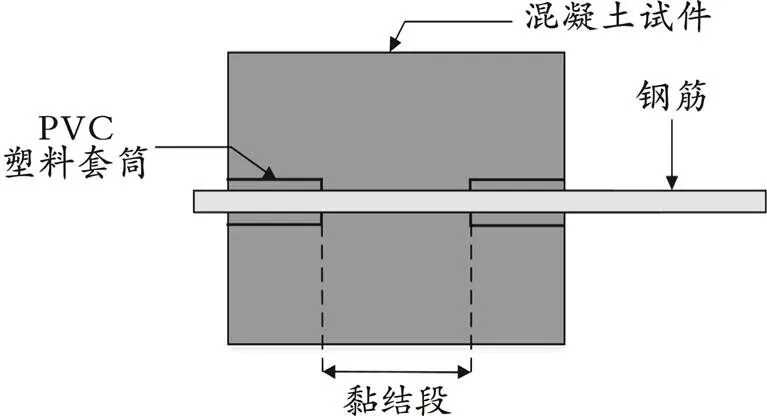
图3 拉拔试件示意图

2.2 钢筋混凝土黏结⁃滑移数值仿真

本文采用牟晓光[14]的钢筋混凝土局部黏结⁃滑移试验数据，对基于ABAQUS的钢筋混凝土黏结⁃滑移有限元模型进行内聚力参数标定。为了避免动态响应的影响，数值仿真采用准静态加载方法。钢筋混凝土黏结⁃滑移模型如图4所示。其中，混凝土块的尺寸为150.0 mm×150.0 mm×150.0 mm，钢筋的长度和直径分别为200.0 mm和9.0 mm。

为了监测钢筋相对于混凝土的滑动位移，在钢筋加载端设置力面耦合点RP⁃1（见图4（a））。将RP⁃1作为滑移监测点，通过有限元计算得到该点的位移和荷载，获得反映钢筋混凝土黏结⁃滑移行为的荷载⁃位移响应曲线。加载端以位移方式进行加载，加载位移为3.0 mm，分析步稳定时间为1×10－10s。为保证数值模拟结果的准确性，分别在加载端和自由端加入PVC套筒，钢筋两端的非黏结段套在PVC套筒中，防止在拉拔过程中加载端应力过大，避免混凝土发生局部破坏而导致预测结果不准确。此外，钢筋中间的黏结段长度为45.0 mm，黏结段在中间应力分布更均匀。混凝土块四周节点设置固定约束，为避免模型表面约束点处翘曲变形过大从而导致网格划分不准确，将混凝土几何模型划分为八等份，然后进行相应的网格离散。其中，混凝土的网格尺寸为6.0 mm，钢筋的网格尺寸为5.0 mm，网格类型均为六面体。

图4 钢筋混凝土黏结⁃滑移模型

考虑实际工程中钢筋与混凝土之间没有缝隙，选用无厚度内聚力建模方法（Surface⁃Based Cohesive Behavior），旨在钢筋与混凝土之间赋予内聚力，从而当钢筋和混凝土发生相对滑动时，在界面处产生黏结力，即钢筋表面的剪应力。有限元模型中的材料参数和内聚力参数分别见表1[14]和表2。内聚力参数中损伤起始强度和能量根据吴业飞等[11]给定的参数范围取值，的取值范围为0.5～1.0 N/mm。当在给定的拟合参数范围内时，若较大，则可以准确地得到其他试件的极限荷载。依据宋启根[18]得出的混凝土界面层刚度约为混凝土弹性模量的75%的结论进行取值。

表1 有限元模型中的材料参数

表2 有限元模型中的内聚力参数

对本文建立的有限元仿真模型的预测结果（本文的计算结果，下同）与文献[14]的试验结果进行了对比，并绘制了钢筋混凝土黏结⁃滑移行为的荷载⁃位移曲线，结果如图5所示。由图5可以看出，有限元模型预测得到的光圆钢筋荷载⁃位移曲线预试验结果的吻合效果较好，荷载增加和峰值点过后的下降趋势基本相同。

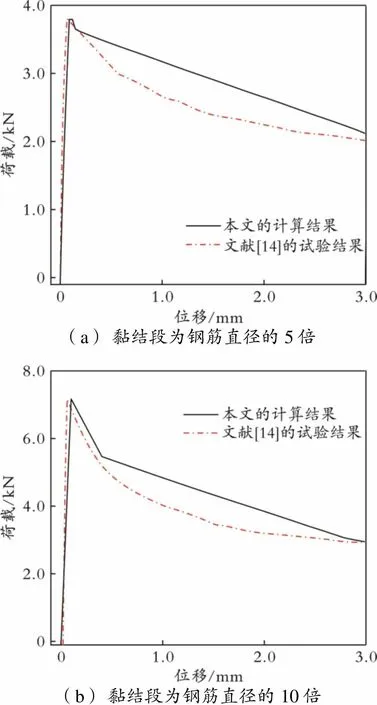
（a）黏结段为钢筋直径的5倍 （b）黏结段为钢筋直径的10倍

值得注意的是，有限元模型预测峰值点后曲线下降幅度略高于试验结果，这是由于本文采用了形式更为简单且参数更少的双线型内聚力本构模型。如果未来研究中需要更多地关注峰值点后下降段部分，可以通过采用指数型内聚力本构模型描述钢筋混凝土黏结⁃滑移行为的损伤演化规律。虽然内聚力双线型、指数型和梯形本构模型分别对应不同的损伤演化阶段，但是通过这三种本构模型得到曲线的发展趋势基本相同[19]。

决定荷载⁃位移曲线趋势的主要因素为内聚力参数；无厚度内聚力模型建模的本质为赋予钢筋混凝土界面黏结力，而内聚力主要存在于内聚力单元，因此网格尺寸的划分直接决定内聚力单元尺寸的大小。鉴于内聚力模型本质特征决定其具有较强的网格敏感性，亟待对钢筋混凝土黏结⁃滑移行为的有限元模型进行网格尺寸敏感性分析。

3 有限元模型的敏感性分析

3.1 模型计算及网格参数的选取

根据过镇海[20]给出的光圆钢筋与混凝土之间的黏结性能，本文将黏结段长度设定为钢筋直径的5倍。因此，以黏结段长度45.0 mm为例，从荷载⁃位移曲线的力学形态角度探究网格敏感性。为探究基于内聚力的钢筋混凝土黏结⁃滑移模型的网格敏感性，设定钢筋和混凝土为各向同性且不含预制裂纹的材料。采用ABAQUS自带的网格划分工具对钢筋和混凝土模型进行网格划分。钢筋的网格尺寸保持恒定（5.0 mm），混凝土的网格尺寸分别为6.0、8.0 mm和10.0 mm。为保持数值模拟结果的准确性，对黏结段的网格加密处理，加密的网格尺寸为1.5 mm。钢筋和混凝土的单元为六面体单元，单元类型为三维实体8节点减缩积分单元（C3D8R），减缩积分单元可以更好地承受单元的扭曲变形，对计算精度几乎没有影响。有限元模型单元信息及节点信息见表3。

表3 有限元模型单元信息及节点信息

3.2 网格尺寸对荷载⁃位移结果的影响

在保持内聚力参数（见表2）相同的情况下，绘制了通过不同网格尺寸模型预测的荷载⁃位移曲线，结果如图6所示。由图6可以看出，在加载方式相同的情况下，三条曲线的发展趋势基本相同，均是随滑动位移的增加，钢筋的极限拉拔荷载快速增大到峰值，然后由极限拉拔荷载引起钢筋继续滑移，直到钢筋从混凝土中完全拔出。

图6 钢筋混凝土黏结⁃滑移过程的荷载⁃位移曲线

上述现象可以通过能量的角度结合内聚力双线型本构模型进行解释，荷载⁃位移曲线所包围的面积可视为模型变形能。在加载初期，黏结段表面的内聚力单元未发生分离，三维实体单元的变形主要为弹性形变。由于模型产生相同的位移所需外部能量相同，而这些能量终归要分配到每个内聚力单元中，因此网格尺寸越大，内聚力单元的数量越少，单个单元承载的能量就越大。若将模型的荷载⁃位移曲线转化为每个单元的荷载⁃位移曲线，则单元在加载位移不变的情况下，只能通过增大峰值点的曲线斜率增加曲线包围的面积，以此获得更多的能量。

3.3 内聚力参数敏感性

针对钢筋混凝土黏结⁃滑移模型，以网格尺寸为6.0 mm的模型、黏结长度为5倍直径的工况为例，从曲线的力学形态角度，探究了有限元模型的内聚力参数敏感性。内聚力参数对荷载⁃位移曲线的影响如图7所示。

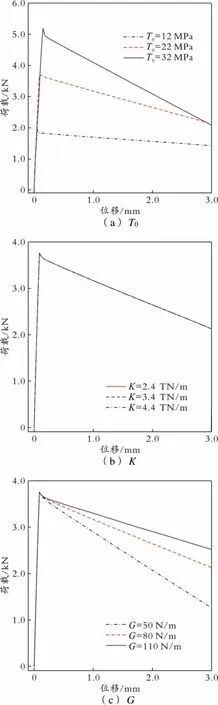
（a）T0 （b）K （c）G

由图7（a）可以看出，在和相同的情况下，荷载峰值随着0的增加而增加。造成这种现象的原因是：相同的外部荷载给予模型相同的能量，0过大使荷载峰值提高，该能量不能维持峰值后的斜率下降速度正常。当0过小时，引起荷载峰值下降，这是由于内聚力单元承载的能量过大，进而引起下降段的曲线斜率大于正常的下降段曲线斜率。

由图7（b）可以看出，对曲线的整体趋势几乎没有影响，的大小仅对曲线峰值有非常小的影响；峰值随着的增加而略微提高，但其影响基本可以忽略不计。这是因为：0影响材料刚度，当不变时，在荷载⁃位移曲线的弹性阶段，随着0的增大，呈线性增大的趋势[11]。因此，当0和保持不变时，的变化对荷载⁃位移曲线的弹性阶段几乎没有影响。在拉拔过程中，钢筋混凝土黏结部分由于黏结力的作用使混凝土逐渐产生微裂纹。因此，混凝土界面层刚度比混凝土的弹性模量要低一些，其值约为混凝土弹性模量的75%，符合文献[18]对取值定义。由图7（c）可以看出，对峰值前的斜率和曲线峰值几乎没有影响，的增大引起峰值后下降段斜率的减小。

4 黏结⁃滑移行为预测的机器学习模型

基于以上有限元模型的敏感性分析结果可知，本文提出的基于内聚力模型的钢筋混凝土黏结⁃滑移有限元模型能够合理地体现钢筋混凝土界面处变形规律及失效行为。但是，有限元仿真建模和计算速度相对较慢，且需要对商业有限元软件参数进行系统标定才能完成上述仿真工作。因此，基于上述通过验证和标定的有限元仿真所获得的预测结果，本文提出并训练得到了一种机器学习的方法，可实现对钢筋混凝土黏结⁃滑移响应的快速评估。在钢筋加载端产生的荷载不断向自由端和混凝土传递过程比较复杂，为了更好地评价黏结长度、钢筋直径及加载方式对钢筋混凝土黏结强度的影响，考虑到小样本、多因素的客观原因会使黏结强度的离散性较大[21]，选取非线性自回归动态神经网络模型。

4.1 NARX动态神经网络

NARX（Nonlinear autoregressive models with exogenous inputs）全称为非线性自回归动态神经网络模型。NARX主要由输入层、隐藏层、输出层以及输入延时和输出延时组成。一般情况下，应用NARX进行预测前需要确定隐藏神经元的个数、输入延时和输出延时阶数。该模型具有良好的记忆和反馈功能，其优势在于可以记录任意时刻的数据，同时将此数据保留并加入到下一时刻进行计算，进而能够有效地得到预测模型结果[22]。NARX动态神经网络模型函数关系可以表示为：

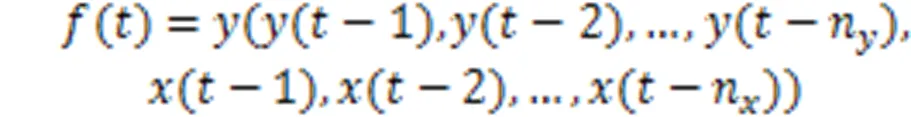
式中：（－1）、（－1）分别为－1时刻的输出序列和输入序列；（－n）、（－n）分别为历史输出序列和历史输入序列；n、n分别为输入延时、输出延时。由式（6）可以看出，（）取决于前一时刻的（）和（）。

NARX动态神经网络流程图见图8。根据图8所示的计算流程，引用表1中的参数，经有限元分析软件批量仿真并提取20组数据，对所建立的NARX进行了训练。其中，将钢筋的滑移量和滑移时间作为输入层，钢筋的历史荷载作为输出层，其目的在于提高计算速度并降低数据分散导致的误差，通过对数据进行非线性处理，实现荷载⁃位移曲线的可靠预测。图8中，（）为时刻的输入序列，（）为时刻的输出序列，为连接权，为隐藏层，为非线性函数，为输入延时和输出延时所对应的延时时间。

图8 NARX动态神经网络流程图

4.2 基于NARX的钢筋混凝土黏结强度预测

按照NARX默认模型参数取值，输入延时为1∶2，输出延时为1∶2，隐层神经元个数为10。为了准确地对NARX进行训练和验证，按照机器学习模型研究的常见方法，将80%的模拟数据作为训练集，10%的模拟数据作为验证集，10%的模拟数据作为测试集。样本总数为20组，按照上述划分原则得出训练样本数为16个，验证样本数为2个，测试样本数为2个，其中样本参数采用随机划分的方式划分。为了评价模型预测的精准度，采用均方根误差（RMSE）、平均绝对百分误差（MAPE）作为评价指标[23⁃26]。RMSE及MAPE的表达式见式（7）—（8）。

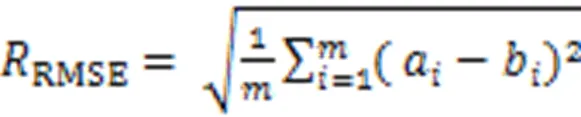
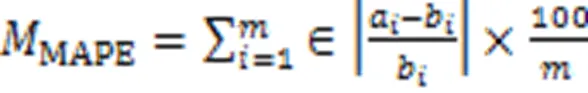
式中：为数据个数；a为实际的荷载⁃位移曲线数据；b为预测的荷载⁃位移曲线数据。

设定钢筋直径为9.0 mm，黏结段长度为45.0 mm和90.0 mm，在滑移量分别为3.0、5.0、15.0 mm和20.0 mm的情况下，对比了机器学习和数值模拟的结果，结果如图9所示。

图9 不同条件下有限元分析的钢筋荷载⁃位移曲线

由图9可以看出，在黏结段长度为45.0 mm时，NARX预测得出的测试集曲线与ABAQUS有限元软件计算得出的曲线几乎处于重合状态；在黏结段长度为90.0 mm时，NARX预测曲线峰值前的斜率略小于ABAQUS有限元软件仿真预测曲线，其原因主要为黏结段长度为90.0 mm的有限元软件计算得出的峰值点前的数据较少，导致预测曲线出现偏差，但两条曲线的误差较小，表明预测结果较好。

NARX的预测结果如图10所示。由图10（a）可知，训练集、测试集和验证集训练效果较佳，预测模型训练总次数为17次，训练11次后误差明显上升，表明模型训练可以结束，样本误差值为0.008。由图10（b）可以看出，模型的训练集、测试集和验证集数据点均在拟合线附近，经计算得相关系数为0.996。由图10（c）和图10（d）可以看出，滞后数（后一时刻数据相对于前一时刻数据的延迟数）为0时误差最大，其余数据点误差几乎均在置信区间内，输入层数据与误差的自相关系数均在0刻度线附近，说明NARX预测结果准确性较高，所建立的NARX能够很好地揭示钢筋混凝土黏结⁃滑移响应的参数规律。

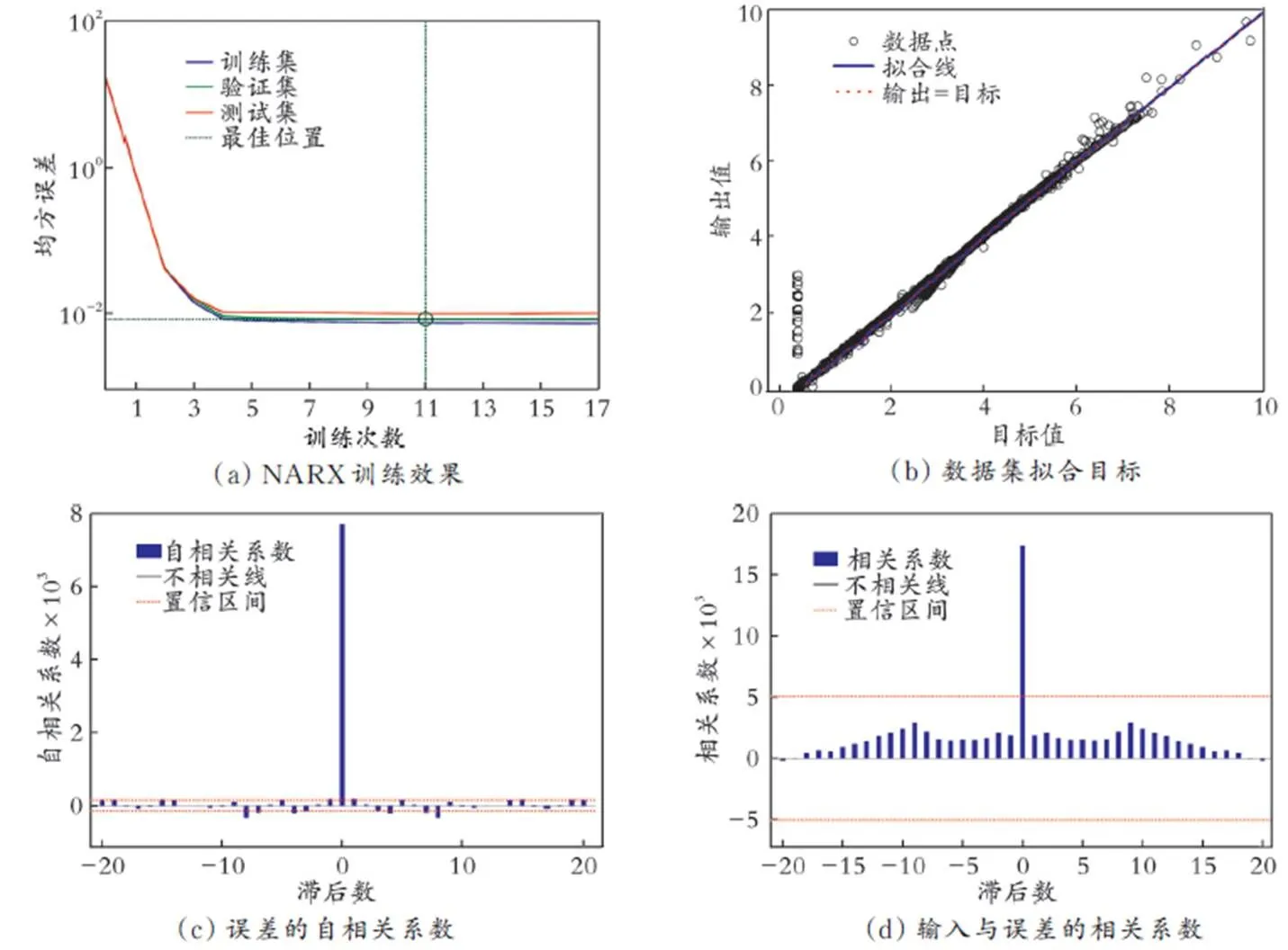
图10 NARX模型预测结果

5 结 论

1）从能量的角度对网格敏感性进行了分析。结果表明，网格尺寸过大会造成有限元预测模型荷载⁃位移曲线对钢筋极限拉拔荷载的预测峰值偏低，但曲线的发展趋势近乎相同。网格尺寸对钢筋混凝土黏结⁃滑移弹性变形主导的牵引⁃分离阶段没有影响，因此可在大尺寸结构数值仿真模型的应力较小处采用较大的网格尺寸，从而显著降低计算成本。从黏结⁃滑移响应曲线的力学形态研究发现，有限元预测模型对内聚力主要参数的敏感程度从大到小的顺序依次为0、和。其中，0影响曲线的峰值以及峰值后下降段斜率，对峰值后下降段斜率影响较大，对曲线力学形态的影响可忽略。

2）通过ABAQUS有限元分析软件，建立有限元预测模型并获取了不同工况下的黏结⁃滑移仿真数据；将数据样本引入NARX进行了预测。通过NARX预测了钢筋混凝土黏结⁃滑移数据，并与有限元仿真数据进行了对比。结果表明，NARX预测精度高，其值达到99.0%以上，说明NARX可以很好地代替耗时且费力的有限元仿真和试验工作。

［1］ 阚呈.油气管道隧道喷锚永久支护结构及其设计方法研究［D］.成都：西南交通大学，2016.

［2］ 马国锐，刘永升，孙宇宸，等.海底单层管道铺管端部受力数值分析［J］.石油机械，2022，50（2）：66⁃73.

MA G R，LIU Y S，Sun Y C，et al.Numerical analysis of stress on pipelaying end of subsea single⁃layer pipeline［J］.China Petroleum Machinery，2022，50（2）：66⁃73.

［3］ 刘伟.油气公共管廊混凝土框架装配式螺栓连接关键技术研究［J］.工程建设与设计，2020（24）：161⁃162.

LIU W.Research on the key technology of assembled bolt connection of concrete frame of oil and gas public pipe gallery［J］.Construction & Design for Engineering，2020（24）：161⁃162.

［4］ 孙杨，乔国富.锈蚀钢筋与混凝土粘结性能研究综述［J］.材料导报，2020，34（3）：122⁃131.

SUN Y，QIAO G F.Research on the bond properties between corroded reinforcing steel bar and concrete：A Review［J］. Materials Reports，2020，34（3）：122⁃131.

［5］ WANG X L，LIU Y Q，YANG F，et al.Effect of concrete cover on the bond⁃slip behavior between steel section and concrete in SRC structures［J］.Construction and Building Materials，2019，229：116855.

［6］ SUN Z Y，FENG D C，SUN Y L，et al.Bond⁃slip behavior of bundled steel/FRP bars and its implementation in high⁃fidelity FE modeling of reinforced concrete beams［J］.Construction and Building Materials，2021，286：122887.

［7］ ROLLAND A，ARGOUL P，BENZARTI K，et al.Analytical and numerical modeling of the bond behavior between FRP reinforcing bars and concrete［J］.Construction and Building Materials，2020，231：117160.

［8］ WANG Z H，LI L，ZHANG Y X，et al.Bond⁃slip model considering freeze⁃thaw damage effect of concrete and its application［J］.Engineering Structures，2019，201：109831.

［9］ 郑山锁，杨路，姬金铭，等.冻融RC梁抗震性能与数值模拟方法［J］.振动工程学报，2021，34（5）：889⁃898.

ZHENG S S，YANG L，JI J M，et al. Seismic behavior and numerical modelling method of RC beams subjected to freezing⁃thawing damage［J］.Journal of Vibration Engineering，2021，34（5）：889⁃898.

［10］ MUKHTAR F M，SHEHADAH M E.Experimental verification of 2⁃and 3⁃D numerical models for bond⁃slip behavior of CFRP⁃concrete［J］.Construction and Building Materials，2021，287：122814.

［11］ 吴业飞，陈伟球.基于内聚力模型的FRP⁃混凝土粘结强度分析［J］.工程力学，2010，27（7）：113⁃119.

WU Y F ， CHEN W Q. Cohesive zone model based analysis of bond strength between FRP and concrete［J］.Engineering Mechanics，2010，27（7）：113⁃119

［12］ HE J，XIAN G J，ZHANG Y X.Numerical modelling of bond behaviour between steel and CFRP laminates with a ductile adhesive［J］.International Journal of Adhesion and Adhesives，2021，104：102753.

［13］ 谢浩，陈思斌，黄永亮，等.基于内聚力模型的网格尺寸及参数敏感性研究［J］.山东大学学报（工学版），2021，51（6）： 111⁃118.

XIE H， CHEN S B， HUANG Y L，et al. Meshsize and parameter sensitivity based on cohesive zone model［J］.Journal of Shandong University （Engineering Science），2021，51（6）：111⁃118.

［14］ 牟晓光.高强预应力钢筋粘结性能试验研究及数值模拟［D］.大连：大连理工大学，2005.

［15］ RANKOVIC V，GRUJOVIC N，DIVAC D，et al.Development of support vector regression identification model for prediction of dam structural behaviour［J］.Structural Safety，2014，48：33⁃39.

［16］ OLALUSI O B，AWOYERA P O.Shear capacity prediction of slender reinforced concrete structures with steel fibers using machine learning［J］.Engineering Structures，2021，227：111470.

［17］ DAI L，WU X，ZHOU M R，et al.Using machine learning algorithms to estimate the compressive property of high strength fiber reinforced concrete［J］.Materials，2022，15（13）：4450.

［18］ 宋启根.用有限元法探讨钢筋混凝土粘结试件［J］.南京工学院学报，1981（4）：100⁃115.

SONG Q G. Study of reinforced concrete bond specimens by finite element method［J］.Journal of Nanjing Institute Eechnology，1981（4）：100⁃115.

［19］ CORNEC A，SCHEIDER I，SCHWALBE K H.On the practical application of the cohesive model［J］.Engineering Fracture Mechanics，2003，70（14）：1963⁃1987.

［20］ 过镇海.钢筋混凝土原理［M］.3版.北京：清华大学出版社，2013.

［21］ 雷进生，陈建飞，王乾峰，等.混凝土中锚杆锚固强度的SVM回归模型［J］.长江科学院院报，2015，32（1）：117⁃120.

LEI J S，CHEN J F，WANG Q F，et al. Regression model of bolt anchoring strength in concrete based on SVM［J］. Journal of Yangtze River Scientific Research Institute，2015，32（1）：117⁃120.

［22］ RAI A，UPADHYAY S H.The use of MD⁃CUMSUM and NARX neural network for anticipating the remaining useful life of bearings［J］.Measurement，2017，111：397⁃410.

［23］ 王婧慈，郭海敏，令狐松，等.多因素水淹强度指数在剩余油评价中的应用［J］.特种油气藏，2015，22（1）：103⁃106.

WANG J C，GUO H M，et al. LING H S， Multi⁃factor water⁃out index application in residual oil evaluation［J］.Special Oil and Gas Reservoirs，2015，22（1）：103⁃106.

［24］ 常亮，樊四良，郭丙君.一种BUCK变换器的滑模⁃通用模型控制器研究［J］.石油化工高等学校学报，2009，22（4）：95⁃98.

CHANG L，FAN S L，GUO B J. A slide mode control⁃common model control controller for BUCK converter［J］.Journal of Petrochemical Universities，2009，22（4）95⁃98.

Sensitivity Analysis and Machine Learning Model for Reinforced Concrete Bond⁃Slip Behavior

LI Hongwei1， WANG Wenwu1， JIA Fengrui2， SU Yutai3， LONG Xu3

（1.School of Civil Engineering，Liaoning Petrochemical University， Fushun Liaoning 113001，China；2.Yangtze Delta Region Institute of Tsinghua University，Jiaxing Zhejiang 314006，China；3.School of Mechanics，Civil Engineering and Architecture，Northwestern Polytechnical University，Xi'an Shaanxi 710072，China）

Aiming at the bond⁃slip behavior of reinforced concrete, the finite element model of reinforced concrete bond⁃slip based on cohesion model was constructed by ABAQUS finite element software. The mesh sensitivity and cohesion parameter sensitivity of the simulation model were explored by energy and load⁃displacement curves. Aiming at the problem of bond strength of reinforced concrete, a nonlinear autoregressive exogenous network (NARX) was developed to predict the load⁃displacement curve for reinforced concrete by creating 20 sets of data with the variables of bond length, reinforcement diameter, and loading method. The study shows that the mesh size of 6 mm provides an ideal balance between prediction accuracy and computational cost. Based on the sensitivity of the finite element prediction results, the cohesive parameters are in the sequence of damage initiation strength, fracture energy, and stiffness. The NARX with the prediction accuracy of 99.6% is promising to replace time⁃consuming numerical simulations and experimental works to achieve an efficient and accurate prediction of the bond strength of reinforced concrete. Such an efficient and accurate prediction method provides a novel and convenient methodology of predicting and designing the bond strength of reinforced concrete.

Reinforced concrete bond⁃slip behavior； Cohesive parameters； Mesh size； Sensitivity analysis； NARX

TE832；TU375.4

A

10.12422/j.issn.1672⁃6952.2024.01.009

2022⁃12⁃20

2023⁃02⁃07

国家自然科学基金项目（52175148，51508464）；陕西省重点研发计划国际科技合作计划项目（2021KW⁃25）。

李宏伟（1999⁃），男，硕士研究生，从事结构工程方面的研究；E⁃mail：2231195327@qq.com。

龙旭（1983⁃），男，博士，副教授，博士生导师，从事结构工程方面的研究；E⁃mail：xulong@nwpu.edu.cn。

李宏伟,王文武,贾冯睿,等.钢筋混凝土黏结⁃滑移行为敏感性分析及机器学习模型[J].辽宁石油化工大学学报,2024,44(1):55-63.

LI Hongwei,WANG Wenwu,JIA Fengrui,et al.Sensitivity Analysis and Machine Learning Model for Reinforced Concrete Bond⁃Slip Behavior[J].Journal of Liaoning Petrochemical University,2024,44(1):55-63.

（编辑 宋锦玉）