基于GA-ACO-BP神经网络的日用消费品物流需求预测
2024-02-23王琰琰任俊玲
王琰琰,任俊玲
(北京信息科技大学 信息管理学院,北京 100192)
0 引言
2022年我国全年零售额约44万亿元,同比下降0.2%;但是线上消费品零售表现突出,实物网上零售额近12万亿元,同比增长6.2%。城镇化速度的加快、居民可支配收入的提升促进了消费能力和消费意愿的不断增强,推动日用消费品的物流需求增长。虽然我国物流产业发展迅速,但是依然无法满足极速增长的物流需求。特别是日用消费品领域,极速增长的物流需求不断引发物流企业运力不足、运送时效不准、物流爆仓等难题。如何精准预测日用消费品物流需求,成为各物流企业在市场竞争中及时调整布局、占据竞争优势所面临的问题。
Yu[1]设计了改进的自适应遗传算法和反向传播神经网络(improved adaptive genetic algorithm and back propagation neural network,IAGA-BP)模型预测重庆市物流需求,该模型在区域物流需求预测中具有较高的预测精度。Zeng等[2]构建的基于弱化缓冲算子的灰色预测模型能较为精准地预测广东省农村物流需求。Yang[3]利用BP神经网络模型对沿海港口物流需求进行预测,该模型具有较高的预测精度。Zhou等[4]提出的一种基于模拟退火粒子群优化-反向传播神经网络(simulated annealing particle swarm optimization-back propagation neural network,SAPSO-BP)的组合预测模型在对货运量的预测中具有较好的收敛性能和稳定性。Gao等[5]提出了一种在一定范围内搜索二维空间(目标、扩散)最优解的参数寻优方法,建立了基于径向基函数(radial basis function,RBF)神经网络的组合预测模型对物流需求进行预测。王晓平等[6]构造了遗传算法优化BP神经网络模型,对北京市城镇农产品冷链物流需求进行预测。蔡婉贞等[7]提出基于BP-RBF的组合预测模型预测港口物流需求,该组合模型的预测结果较为稳定可靠。李敏杰等[8]采用RBF神经网络模型对水产品冷链物流需求进行预测,该模型能较为准确地预测水产品冷链物流需求。王晓平等[9]考虑到农产品冷链物流需求系统具有复杂特征,采用支持向量机模型对北京城镇农产品冷链物流需求预测,该模型能够很好地拟合冷链物流需求。张国玲等[10]提出一种基于差分自回归移动平均反向传播神经网络(auto regressive integrated moving average back propagation neural network,ARIMA-BPNN)的物流需求量预测模型,相较于其他预测模型有较高的预测精度。
相较于简单的线性系统,物流系统属于庞大且复杂的非线性系统[11]。日用消费品物流需求的影响因素多且复杂,影响因素之间存在多重共线性。以线性回归法为代表的部分传统预测方法不能准确地刻划日用消费品物流需求中的非线性关系,导致预测精度不够[12]。另外,日用消费品物流可采用的历史数据较少,部分预测方法不能够充分训练而导致预测精度较低。因此,在选择预测方法时要考虑这些因素,选出更为准确、有效的预测方法。
考虑到日用品物流需求的数据样本较少,本文选取BP神经网络模型对日用消费品物流需求进行预测,并引入遗传算法(genetic algorithm,GA)和蚁群优化(ant colony optimization,ACO)算法对其进行优化,避免模型陷入局部最优,提高预测精度,得到更为精准的预测结果,以帮助企业规划物流需求,给予消费者更好的物流体验。
1 日用消费品物流需求预测思路
日用消费品与日常生活息息相关,在互联网的支持下,电商及新零售产业发展迅速,线上购买日用消费品的便捷、速度和实惠不断促进日用消费品物流需求的增长,而需求的增长却在不断向物流的供给施加压力。本文通过预测日用消费品物流需求帮助企业规划物流供给,以达到市场的供需平衡。具体预测思路如图1所示。

图1 预测思路Fig.1 Prediction idea
首先,对日用消费品物流需求的相关影响因素进行分析总结。然后,将历史数据代入灰色关联度分析模型,对日用消费品物流需求影响因素进行筛选,得出与日用消费品物流需求关联度较高的预测指标。最后,构建基于GA-ACO-BP神经网络的预测模型。将筛选过后的预测指标的历史数据代入模型进行训练和测试。根据训练结果对模型参数进行调整,达到较高的预测精度后,使用该模型对未来的日用消费品物流需求进行预测。
2 构建预测指标体系
2.1 日用消费品物流需求影响因素分析
居民作为日用消费品的直接消费端,其规模程度、经济水平和生活水平对日用消费品的消耗量有直接影响。而物流业作为经济发展的派生需求,其市场需求与经济发展形成了相辅相成、相互促进的关系。本文结合现有的文献研究,从日用消费品物流供需的角度出发,将影响日用消费品物流需求的影响因素分为以下6类:
1)宏观经济发展水平。经济发展程度决定了居民生活水平的高度以及物流业的发展速度。经济越发达,人们的生活水平越高,对产品质量和时间消耗的要求就越高,对物流服务的需求更大也更严苛。
2)相关产业水平。产业结构的不同决定了物流需求结构的不同。日用消费品物流连接消费品市场的上下游,相关产业的发展水平与日用消费品物流的发展相辅相成。
3)消费能力。居民作为日用消费品的最终用户,其收支水平和人口规模对于日用消费品市场有直接的影响。
4)物流供应能力。物流供应能力可以反映交通运输水平,物流能力会影响物流服务和物流效率,进而影响需求。
5)互联网发展水平。伴随互联网的发展,电商行业发展迅速。电商平台作为居民线上购买日用消费品的渠道,对于日用消费品的物流需求有着决定性的影响作用。
6)贸易水平。国内贸易在物流行业的发展初期产生了大量需求,而国际贸易的不断发展、居民消费能力的提升、对消费品的高要求都在推动跨境电商行业的发展,随之产生的进出口日用消费品物流需求不容忽视,因此选取进出口总额指标衡量贸易水平和进出口的日用消费品物流需求的发展潜力。
本文遵循指标选取的可获得性、实际性和全面性原则,选取宏观经济发展水平、相关产业水平、居民消费能力、物流供应能力、互联网发展水平、贸易水平共6个一级指标,在此基础上分析总结了13个影响因素作为二级指标,如表1所示。

表1 全国日用消费品物流需求影响因素Table 1 Factors affecting the logistics demand for daily consumer goods in China
2.2 基于灰色关联度分析的预测指标筛选
2个系统之间的因素,随时间或不同对象而变化的关联性大小的量度,称为关联度。2个因素变化即同步变化程度越高,二者关联程度越高;反之,则越低。因此,灰色关联分析方法,根据因素之间发展趋势的相似相异程度,为衡量因素间关联程度提供了量化的度量[13]。灰色关联度适用于“小样本、贫信息”,根据序列曲线几何形状的相似程度来判断其联系是否紧密,不受主观因素影响,是一种客观的指标筛选方法。
反映系统行为特征的参考序列记为Y=y(k)(k=1,2,…,n),影响系统行为特征的比较序列记为Xi=xi(k)(i=1,2,…,m),δi(k)为xi(k)与y(k)之间的关联系数,定义为
δi(k)=
(1)
式中:ρ为分辨系数,取值范围为(0,1),通常取0.5。
ri为Y与Xi之间的关联度,定义为
(2)
关联度越大,相关性越高。
本文通过查找国家统计局、中华人民共和国商务部和中国互联网信息中心的相关数据及资料,整理出全国日用消费品物流需求量及其13个影响因素从2010年到2022年共13年每年的相关统计数据。以全国日用消费品物流需求量为参考序列Y=y(k)(k=1,2,…,13),13个影响因素为Xi=xi(k)(i=1,2,…,13),计算得出全国日用消费品物流需求量(Y)与其影响因素之间的灰色关联度,如表2所示。

表2 全国日用消费品物流需求量与影响因素关联度Table 2 Correlation between daily consumer goods logistics demand and influencing factors in China
从表中数据对影响因素对应的关联度进行排序,可得出:X1>X3>X5>X12>X4>X8>X13>X6>X2>X11>X9>X7>X10。
根据文献调研,通常关联度结果大于0.7就表示具有较强的相关性,因此本文选取关联度结果大于0.7的8个影响因素作为预测指标,分析各项预测指标对日用消费品物流需求的影响程度。分别是人均GDP(X′1);第三产业增加值(X′2);批发与零售业增加值(X′3);居民人均可支配收入(X′4);居民人均消费支出(X′5);交通运输、仓储及邮政业增加值(X′6);互联网普及率(X′7);进出口总额(X′8)。整理后的各项数据如表3所示。
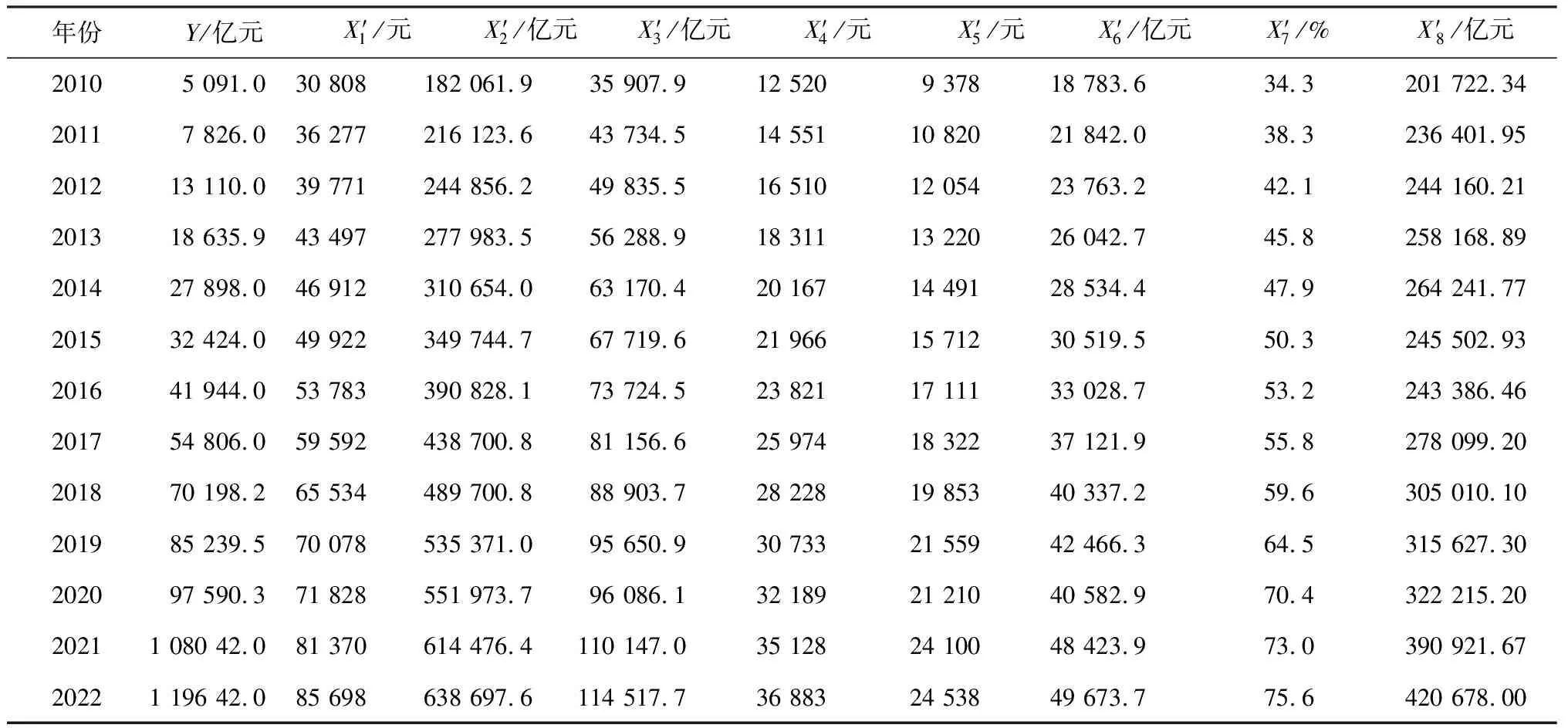
表3 2010—2022年全国日用消费品物流需求输入和输出指标数据Table 3 Input and output indicator data of logistics demand for daily consumer goods in China from 2010 to 2022
3 构建预测模型
为了更为准确地预测日用消费品物流需求,在构建模型时需要选择适配其数据特征的模型。日用消费品物流需求的样本量较少,且影响因素之间存在非线性,因此,需要构建一个能够拟合非线性和小样本的预测模型,才能提高预测精度。
3.1 BP神经网络
BP神经网络是一种高度自适应的非线性动力系统。BP神经网络通过学习可以得到输入与输出之间的高度非线性映射[14],具有很强的非线性模拟、自组织及自学习能力,且对数据量要求不高,非常适合小样本、非线性的物流需求预测。
3.2 构建GA-ACO-BP神经网络预测模型
本文构建了GA-ACO-BP神经网络模型,对日用消费品物流需求进行预测。其过程为:将BP神经网络的权值和阈值作为蚁群算法中蚂蚁种群的路径坐标,计算蚁群算法中每只蚂蚁的适应度值,对比适应度值的大小,将不满足条件的蚂蚁代入遗传算法进行选择、交叉和变异,将满足条件的蚂蚁代入蚁群算法的寻优流程,计算最优个体的状态转移概率和信息素浓度,再次对比适应度值大小,不满足条件的蚂蚁继续循环迭代,将满足条件的蚂蚁坐标作为BP神经网络的最优权值和阈值,代入BP神经网络进行训练直至得出最优结果。具体流程如图2所示。
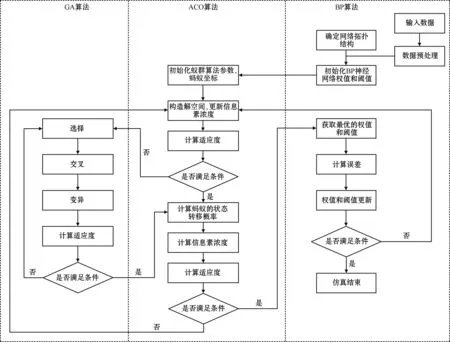
图2 GA-ACO-BP预测模型流程图Fig.2 Flowchart of GA-ACO-BP prediction model
基本步骤如下:
步骤1参数初始化。根据数据集的输入和输出确定BP神经网络,根据输入层的节点数(m)和输出层的节点数(n),并根据经验公式,计算隐含层的节点数(l),如式(3)所示。将产生初始的权值(wij,第i个神经元到第j个神经元的权值)和阈值(bij,第i个神经元到第j个神经元的阈值)组成的所有元素记为集合Iwi;设定误差函数Ei,如式(4)所示。
(3)
(4)
式中:a为整数,通常取值[1,10];Oij为实际值;Dij为预测值。当误差小于设定值时,参数达到最优,停止迭代,输出最优结果。
步骤2构造解空间,计算信息素浓度:
(5)
式中:τij为第i个神经元和第j个神经元之间的信息素浓度,信息素浓度越高,被选中的概率越高;Q为初始信息素浓度;Δwij为第i个神经元到第j个神经元的权值的变换量;Δbij为第i个神经元到第j个神经元的阈值的变换量。
步骤3选定适应度函数并计算适应度值。对不满足条件的蚁群执行遗传算法的选择、交叉、变异。对满足条件的蚁群执行步骤6。针对本文的应用场景,适应度函数为训练样本的实际输出与期望输出之间的误差平方和,采用轮盘赌规则执行遗传算法的选择操作,选择算子计算方式如下:
(6)
式中:Pi为遗传种群中个体配对选择的概率;fi为适应度函数;N为种群中个体的总数。
步骤4交叉操作。将父代个体的基因进行权重随机平均,得到子代的基因,具体过程如式(7)所示:
Z(i)=Pc×F1(i)+(1-Pc)×F2(i)
(7)
式中:Z(i)为通过交叉计算父代个体的基因而产生的新的子代基因;Pc为交叉概率,取值在[0,1]之间;F1(i)为父代F1的第i个基因;F2(i)为父代F2的第i个基因。
步骤5变异操作。高斯变异可以增加种群多样性、提高搜索效率和避免陷入局部最优解,采用高斯变异算子进行变异操作:
(8)
式中:σ为高斯分布的标准差;randn()为随机高斯分布函数,均值为0,标准差为1。
步骤6计算蚂蚁的转移状态概率。
(9)

步骤7更新信息素浓度。
(10)
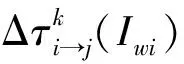
步骤8将寻优结果代入BP神经网络训练,计算训练误差,当误差达到目标要求时,输出结果,否则继续进行步骤2~7。
3.3 实证分析
为了消除样本数据间的量纲影响,按式(11)对全部样本数据进行归一化处理:
(11)
式中:x*为归一化后的数据;x为归一化前的数据;xmin为数据的最小值;xmax为数据的最大值。
将表3中的X′1~X′8作为模型的输入,表3中的Y作为输出,得出GA-ACO-BP神经网络预测模型的输入层节点为8,输出层节点为1。根据式(3)计算该模型的隐含层节点范围为[4,13],通过代入隐含层节点数进行网络训练计算训练集的均方误差,可以看出当隐含层节点数为8时,训练集的均方误差最小,如图3所示,故确定该网络的拓扑结构为8-8-1。

图3 隐含层节点数网络训练结果Fig.3 Network training results for the number of hidden layer nodes
为了进一步验证GA-ACO对BP神经网络的优化效果,选取表3中2010—2019年的数据作为样本数据,按照7∶3的比例划分前7年的数据为训练集,后3年的数据为测试集,并对其进行归一化处理后,代入GA-ACO-BP预测模型。经过不断优化后模型参数设置如表4所示。并与BP神经网络预测模型和GA-BP预测模型的预测结果进行对比。选用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)以及平均绝对百分比误差(mean absolute percentage error,MAPE)这3种评价指标对3种模型进行性能评估,3种指标的值越小说明模型的精度越高。

表4 GA-ACO-BP预测模型参数设置Table 4 GA-ACO-BP prediction model parameter settings
模型训练后的测试结果如表5所示。GA-ACO-BP预测模型的3种误差明显更小,预测精度比GA-BP和BP神经网络预测模型更高,表明GA-ACO对BP神经网络模型有较好的优化效果,提高了预测精度。

表5 各模型预测精度Table 5 Prediction accuracy of each model
3.4 预测结果
利用构建好的GA-ACO-BP预测模型对2020—2022年的日用消费品物流需求进行预测。考虑在实际预测中数据量级较大,对比实际值与预测值之间的差异不够直观,而相对误差能够很直观地帮助比较预测值的精度,本文选择计算并比较3种模型预测结果与实际值之间的相对误差,并通过计算预测结果的平均相对误差以对比3种模型的综合预测效果。输入数据见表3中2020—2022年的数据,模型预测结果如表6所示。由表6可知,3种预测模型的平均相对误差分别为19.17%、11.16%、2.03%,GA-ACO-BP预测模型的预测误差明显更小。该模型在日用消费品物流需求预测中能够达到更好的预测效果,且与真实值保持着较高的拟合度,对于日用消费品物流需求的预测研究具有一定可参考价值。

表6 不同模型测试结果对比Table 6 Comparison of test results for different models
4 结束语
本文从日用消费品的需求端考虑物流需求,以全国网上实物零售总额作为日用消费品物流需求量,分析了供需两端的影响因素,采用灰色关联度分析对影响因素进行筛选,并通过GA-ACO优化BP神经网络模型,对日用消费品物流需求进行预测,并对比了传统BP神经网络模型和GA-BP预测模型的预测效果及精度,实证得出GA-ACO-BP预测模型对日用消费品物流需求预测的有效性,为日用消费品物流需求预测提供了一种较为精确的预测方法,也为其他领域的需求预测研究提供参考。
