土体渗透各向异性对水下隧道渗流量的影响研究
2024-02-23张天骄蒋熠诚
乔 彤,周 建,张天骄,蒋熠诚
(浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310058)
0 引 言
水下隧道采用“堵水限排”的防排水体系时,地下水将透过衬砌流入隧道从而形成渗流场,渗流场形成带来的关键工程问题之一是隧道渗流量,渗流量的准确计算对于水下隧道的建设具有重要意义[1-2]。
国内外学者发现,影响水下隧道渗流量的因素众多,其中隧洞开挖后洞周土体的渗透性和衬砌的渗水模式对于隧道渗流量有巨大的影响[3-4]。对于前者,目前学者大多将地层模型简化成饱和均质且各向同性的多孔连续介质,忽略了自然界土体受地质作用及自身重力影响多表现为各向异性这一基本现实。对于后者,目前衬砌中水的渗流方式主要包括等水压和等水头两种模式:等水压模式不考虑衬砌内衬里及大气压作用,衬砌内缘水压力为0;等水头模式假设衬砌内缘存在不透水衬里时,总水头沿着内缘表面均匀分布,为恒定值。在洞周土体各向同性假设的基础上,EI[5]和GUO等[6]在等水压渗水模式下采用保角变换法对单层半无限介质中的无压孔洞渗流问题进行了研究并给出解析解。国外学者BATU[7]、KOLYMBAS等[8],国内学者童磊等[9]、应宏伟等[10]、王秀英等[11]也在等水头渗水模式下分别采用保角映射、镜像法、竖井法推导了水下隧道渗流场的解析式,并与数值模拟值对比验证。明冬雨等[12]对不同渗水模式下的水下浅埋无压圆形隧道进行了研究,认为等水头渗水模式能更好地满足衬砌外水荷载计算精度的要求。
近些年来,少数学者开始考虑渗透各向异性对于隧道渗流场的影响。徐长节等[13]基于无限含水层竖井理论,通过坐标变换及保角映射法,推导了各向异性渗流下深埋圆形隧洞渗流场解析解,但该方法将半无限渗流域简化为无限渗流域,与实际情况不符,只能算近似解。LI等[14]采用保角映射及最优化技术推导了考虑渗透各向异性的水下圆形隧道渗流场的解析式,并研究了等水压和等水头渗水模式下的隧道渗流量变化情况,但需要利用计算机获取映射函数,因此只能算一种半解析解。
从上述研究中发现,目前的研究多数将水下隧道洞周土体简化成各向同性的多孔连续介质,对于考虑土体渗透各向异性和衬砌渗水模式联合作用下的隧道渗水量的研究未见报道。基于此,本文采用坐标变换和保角映射法,推导了在渗透各向异性下半无限多孔介质中水下隧道渗流量的解析式,并初步探究渗透各向异性、衬砌渗水模式对隧道渗流量的影响。
1 水下隧道计算模型
本文研究对象为考虑渗透各向异性的水下隧道。地层表面以上水头高度为Hw;水下隧道横截面为圆形,衬砌外半径为r1,衬砌内半径为r0,渗透系数为k1;注浆圈外半径为rg,渗透系数为kg;隧道中心到介质距离为h,定义为埋深;洞周土水平向渗透系数为kx,竖直向渗透系数为kz,与渗透主轴方向一致,且均为常数;基准面建立在地层表面,如图1所示。
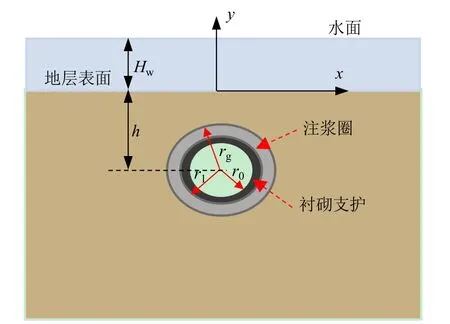
图1 水下隧道模型图Fig.1 Diagram of underwater tunnel
此外,模型基本假设如下:
(1)洞周土为渗透各向异性介质;
(2)隧道处于稳定渗流状态;
(3)水流服从达西定律;
(4)排水以衬砌均匀渗水实现,注浆圈和衬砌内以径向渗流为主。
本文按照等水压和等水头模式模拟隧道衬砌渗水,按照上述假设,可得:
a)地表渗流边界条件是:
b)等水压模式下衬砌内缘渗流边界条件:
c)等水头模式下衬砌内缘渗流边界条件:
式中:Hw是地表水头;h0是衬砌内部水头,通常以隧道拱脚线处水头近似表示。
2 解析解推导
由于隧道洞周土为渗透各向异性介质,注浆圈和衬砌为渗透各向同性介质,直接求解不易。为方便求解,将洞周土区域与注浆圈内区域(包括注浆圈和衬砌)分开计算,再按照渗流连续理论的流量相等原则联立求解[15]。
2.1 等水压渗水模式的渗流量求解
(1)洞周土域内渗流量求解
根据地下水流的连续性原理,均质、各向异性含水层的二维稳定渗流的基本微分方程为:
式(4)为考虑渗透各向异性的稳定渗流控制方程,与传统的各向同性土体中的渗流控制方程拉普拉斯方程不同[16]。拉普拉斯方程在各向同性水下隧道稳定渗流场中的求解已经非常普遍,因此采用坐标转换法将式(4)转化为拉普拉斯方程的形式,再利用现有拉普拉斯方程的求解方法求解水下隧道渗流量。
a)坐标转换,令:
则式(4)转化为式(7)的形式:
式(7)即为拉普拉斯方程形式。
通过式(5)、式(6),原z平面中渗透各向异性渗流场转换为新S平面各向同性渗流场,如图2(a)到图2(b)。变换后渗流场的等效渗透系数为ke,按照不同坐标系下渗流场流量不变原则[17]计算得到ke同时,上述变换也将z平面中圆形book=10,ebook=17内边界变成S平面中椭圆形内边界,若假设椭圆形内边界的长、短轴半径分别为a、b,则:
S平面中的内边界不再是圆形,直接求解困难,可考虑采用保角映射法将S平面中的椭圆形内边界转化为圆形内边界。
b)保角映射过程
由于求解域具有对称性,取一半进行分析,保角映射复变函数式如式(9)~(11)所示。
式中:S=X+iZ;t=ξ+iη;R=(a+b)/2;m= (a−b) /(a+b);u、ν为复变函数w1(S)的实部和虚部;ξ、η分别为复变函数w2(t)的实部和虚部;i为虚数单位。
利用复变函数式(9)~(11)[18-19]可将S平面的椭圆形内边界转变为π平面内圆形内边界,地表保持不变,如图3所示。π平面与原z平面形式类似,求解更加方便。

图3 保角映射过程Fig.3 Conformal mapping process
将h代入式(9)~(11)中,最终可得π平面中隧道的埋深heq如式(12)所示。
式中:n为隧道洞周土体水平向渗透系数与竖直向渗透系数之比,n=kx/ky。
在π平面隧道模型的基础上,进一步利用式(13)的复变函数式[20]将其转化为同心圆环域,方便极坐标下求解。映射函数如下:
式中:τ、A为复变函数w3()τ的实部和虚部。
式(13)将π平面中的地层表面化为半径为1的外圆,内边界AB化为一半径为ε的内圆,对应水头不变。
按照上述保角变换的方法,拉普拉斯方程可以在同心圆环域内表示为下式:
极坐标下该式的通解为:
式中:H为洞周土域水头;C1、C2为待定常数;C3、C4为待定常数族;ρ为极坐标系半径;θ为极坐标系极角;k为常数。
c)方程求解
代入洞周土域地表面边界条件:
设洞周土域内边界水压力为ps,总水头:
其傅里叶级数形式如下:
总水头在λ平面内可表示为:
与式(17)比较两边系数可得:
则洞周土域孔隙水压力表达式为:
洞周土域渗流量Qs可表达为:
(2)注浆圈内的渗流量求解
注浆圈和衬砌以径向渗流为主,则可简化为径向轴对称渗流模式,注浆圈内任一点水压pg满足拉普拉斯方程形式:
代入边界条件:
式中:pg为注浆圈外缘水压力;1p为注浆圈与衬砌交界面水压,衬砌内缘水压力为0。
解得pg后积分可得注浆圈渗流量Qg:
同理衬砌内的渗流量Ql:
(3)水下隧道渗流量的求解
由地下水渗流连续性原理可知,洞周土域与注浆圈域、注浆圈域与衬砌域渗流量相等,即Qs=Qg=Q1,最终联立式(25)、(28)、(29)可得隧道渗流量近似表达式:
2.2 等水头排水模式下的渗流量求解
与等水压渗水模式求解思路一样,但边界条件变为:
式中:hg为注浆圈与洞周土域交界面水头;1h为注浆圈与衬砌交界面水头;0h为衬砌内部水头。直接求解得隧道渗流量:
3 参数分析
为反映不同衬砌渗水模式和渗透各向异性对隧道渗流量的影响,假设某水下隧道地表水头Hw为20 m,隧道埋深h为15 m,衬砌内半径5 m,厚30 cm,内缘孔隙水压力为0。洞周土体为粉砂土,为反映渗透各向异性的影响,设竖直向渗透系数kz=1×10−6m/s,水平向渗透系数kx为变量,令n=kx/kz,代表渗透各向异性比,比值越大,代表土体渗透各向异性越明显。目前对于各类土体渗透系数各向异性的研究还处于定性阶段,对于一般渗透性较好的砂土,渗透各向异性比n值可能在1~15之间,而对于渗透性较差的黏土、淤泥质土,n值可能在20~100之间,变化差异较大[21]。
此外为反映隧道埋深与隧道孔径之间的关系,定义隧道埋深比a=h/r0,本文假设r0不变,通过改变h来改变埋深比a的值。
为验证解析解,利用COMSOL数值软件对不同渗水模式下的渗流量值进行验证,并考虑洞周土渗透各向异性对隧道渗流场的影响。为消除边界影响,模型左右宽度各取10倍埋深,模型深度取6倍埋深。
设衬砌渗透系数k1=5×10−8m/s,两种衬砌渗水模式下的隧道渗流量随n值的变化规律如图4所示。
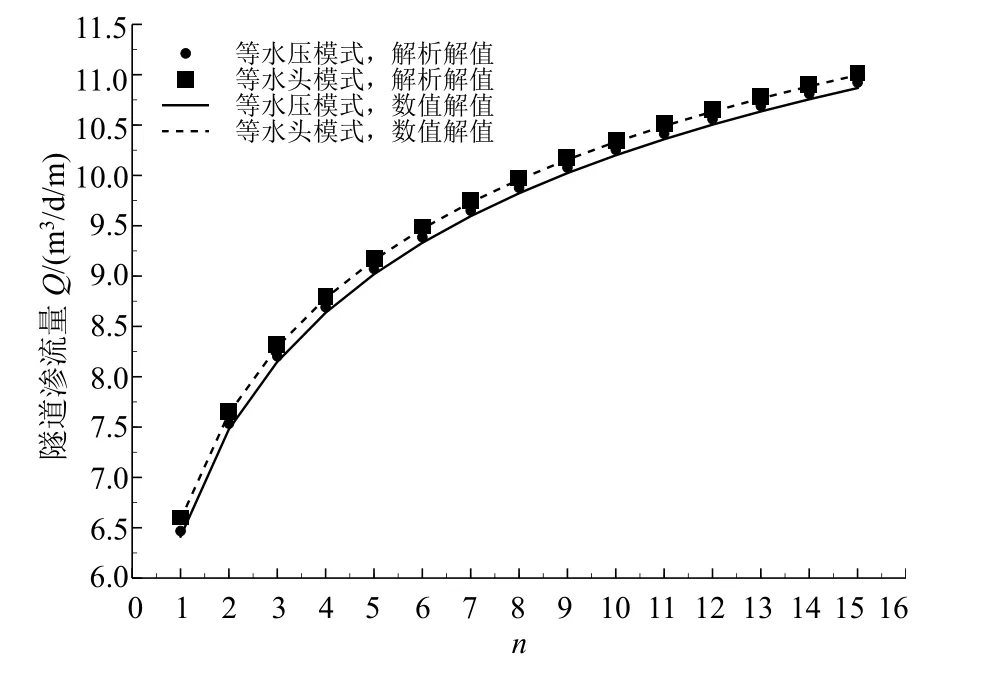
图4 不同渗水模式下的隧道渗流量随渗透各向异性比n值的变化规律Fig.4 Variation of seepage flow with anisotropic permeability index n under different seepage modes
图4中横坐标为水平向与竖直向渗透系数之比n,纵坐标为隧道渗流量Q(m3/d/m)。从图4中看,无论是等水压还是等水头渗水模式,解析解都与数值解拟合较好,整体上解析值大于数值模拟值,但发展规律一致:Q都随着n值的增大而增大,但增长趋势渐渐放缓,考虑渗透各向异性对于Q影响巨大。例如在等水压模式下,n=1(即渗流各向同性)时Q=6.47 m3/d/m,而当n=3、6时Q=8.21、9.38 m3/d/m,相比n=1时Q的增量比为26.89%、44.98%。由此可见若不考虑渗透各向异性,水下隧道渗流量会被低估。
此外,从图4中还可以观察到,等水头渗水模式下的Q略大于等水压渗水模式下的Q,但整体相差不大。主要原因在于a的影响:等水压渗水模式假设衬砌外缘孔隙水压力沿外缘向相等,忽略了位势水头的影响,所以渗流量值小于等水头渗水模式下的渗流量。当a较大时,衬砌内外缘位势水头对渗流场水力梯度的影响微乎其微,两种渗水模式下的渗流量自然相差不大。
为进一步探究埋深比a对上述两种衬砌渗水模式下Q的影响,设r0不变,h为变量,不同渗透各向异性比n下的隧道渗流量随h的变化如图5所示。
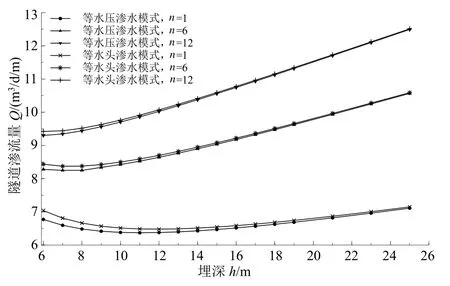
图5 不同n下隧道渗流量随埋深h的变化Fig.5 Variation of seepage flow with h at different n
观察图5,等水头和等水压渗水模式下的隧道渗流量之差随着隧道埋深h的增大而减小。当h较小时,此时位势水头对于Q的作用强烈,两种渗水模式下Q之间的差异相对较大。但随着h增大,如当n=1,h=16 m时,两种衬砌渗水模式下的Q值几乎一致,说明衬砌渗水模式的选择对于浅埋隧道的影响相比大埋深隧道来说更显著。该结论与PARK等[22]基于土体渗透各向同性下两种渗水模式对隧道渗流量影响规律一致,即对于浅埋隧道,无论是否考虑隧道周围土体的渗透各向异性,不同渗水模式下的隧道渗流量差异都比较大。
此外还可以看到,当n=1时,Q在h<11 m时先减小,之后才随着h的增加而增加。而当n=12时的Q值随着h的增加而增加,不存在一个减小的过程。究其原因,当隧道埋深很浅时,隧道接近地表,地下水不再通过土体均匀流入隧道,而是通过隧道上方的薄土层直接进入隧道,低于地表水头Hw,导致隧道渗流量减小。而本例中假设kz不变,渗透各向异性比n值越大代表kx越大,即水平方向上的渗透性越强,浅埋时的水流不再仅从隧道上方流入隧道,而是更倾向于从隧道洞周均匀流入,渗流路径对比如图6所示。且综合n=1、6、12来看,n值越大,隧道渗流量“先减后增”效应越不明显,反映了渗透各向异性对于隧道渗流场的重要影响。
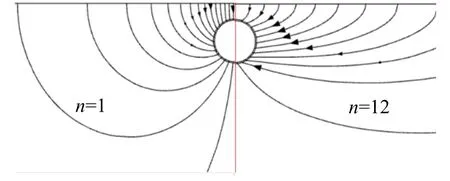
图6 浅埋下n=1与n=12渗流路径对比图(红线左侧为n=1的渗流路径,右侧为n=12的渗流路径)Fig.6 Comparison of seepage paths of n=1 and n=12 in shallow tunnel (left: n=1, right: n=12)
衬砌的存在同样会对隧道渗流量产生一定的作用。为探究衬砌渗透性的影响,假设衬砌渗透系数k1为变量,洞周土竖直向渗透系数kz=1×10−6m/s,令n1=kz/k1,代表洞周土与衬砌渗透性的差异,n1越大,衬砌渗透性越低。埋深15 m、衬砌内径5 m时等水压渗水模式下Q随n1的变化如图7所示。
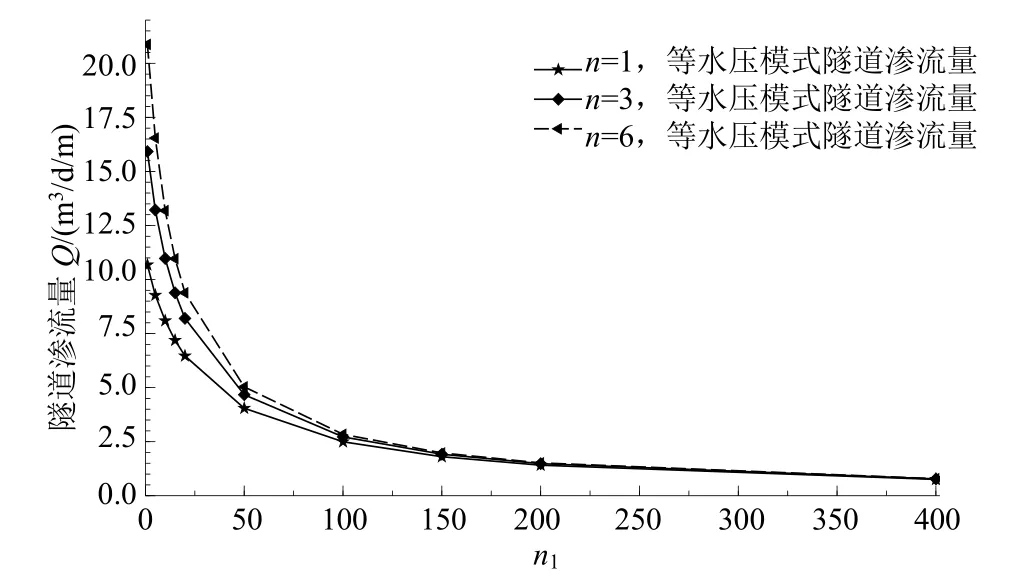
图7 考虑衬砌渗透性影响的Q随n1的变化Fig.7 Variation of Q with n1 under different lining permeability
分析图7可知,等水压模式下隧道渗流量随洞周土与衬砌渗透系数之比n1的增大迅速减小后渐趋于平缓。当n1一定时,不同渗透各向异性比n下的渗流量Q存在一定的差异,说明渗透各向异性是影响隧道渗流量的重要因素之一,且n1越小,衬砌渗透系数越大,n值对Q的影响越大。而随着n1的增大,衬砌渗透性越来越差,与洞周土渗透性差异增大,不同n下的Q越接近。本例中,当nl>100时,n对Q的影响微乎其微,说明当洞周土渗透性较好时,衬砌渗透性对于隧道渗流量的影响相对更大。
上述假设中,洞周土渗透性为1×10−6m/s,渗透性较好,但在我国沿海地区(如上海)土体多为软黏土,渗透系数在1×10−8~1×10−11m/s之间,渗透性极差,与衬砌渗透性的差异较小。下面本文探究软黏土中隧道渗流量与围岩渗透各向异性的关系。假设衬砌渗透系数k1=5×10−9m/s,洞周土渗透系数kz为变量,令n1=kz/k1,取值0.1~10,即洞周土与衬砌渗透性差异在10倍内。软黏土中等水压模式下的Q随n1的变化情况如图8所示。

图8 考虑软土渗透性影响的Q随n1的变化Fig.8 Variation of Q with n1 under different soil permeability
从图8中看,隧道渗流量Q随洞周土与衬砌渗透系数之比n1的增大而增大,且增长趋势几乎是线性的。这说明当洞周土与衬砌渗透性较为接近时,衬砌渗透性对于Q的影响将减弱,而洞周土体渗透性对Q的影响相对加强。如当n1=2,n=3、6的Q值相比于n=1的Q值增量比为47.86%、91.57%;n1=8时的增量比为38.10%、68.31%。说明洞周土与衬砌渗透性越接近,洞周土渗透各向异性对隧道渗流量的影响越大,因此在软黏土等弱透水土体中渗透各向异性对隧道渗流量有更重要的影响。同时要注意的是,洞周土渗透性越差,整体上隧道渗流量也越小,但随着地下水限排规定越来越严格,当土体表现出明显各向异性时,还是不能忽略渗透各向异性对渗流量的影响。图9展示了等水压渗水模式下地表压力水头高度对隧道渗流量的影响。横坐标为地表压力水头Hw(m),纵坐标为隧道渗流量Q(m3/d/m)。从图9中看,隧道渗流量随地表压力水头呈线性增加趋势,即地表压力水头越大,隧道渗流量越大。此外,洞周土渗透各向异性对隧道渗流量的影响也随着地表压力水头Hw的增大而增加。例如Hw=0,n=1时,渗流量Q=2.83 m3/d/m,而当n=3、6时Q=3.60、4.23 m3/d/m,相比n=1时Q的增量值为0.77、1.4 m3/d/m;Hw=40 m时,n=3、6相比n=1时Q的增量值为2.88、5.30 m3/d/m。因此当地表存在高水位时要更重视渗透各向异性对隧道渗流量的影响,才能准确计算隧道渗流量,指导工程建设。

图9 隧道渗流量随地表压力水头的变化Fig.9 Variation of seepage flow with surface water head
4 结 论
(1)本文在假定两种衬砌渗水模式的基础上推导了考虑渗透各向异性的水下隧道渗流量的解析解,为水下隧道渗流量的计算提供了一种方法。
(2)通过参数分析可知,渗透各向异性比n对隧道渗流量会产生显著的影响,不考虑渗透各向异性将低估隧道渗流量。
(3)埋深比a能够影响衬砌等水压和等水头渗水模式下的隧道渗流量,且隧道埋深越小,两种衬砌渗水模式下的隧道渗流量之差越大,浅埋隧道尤其要重视衬砌渗水模式的选择。此外渗透各向异性会改变浅埋隧道的水流渗流路径,使地下水通过土体均匀流入隧道,不是仅通过隧道上方的薄土层直接进入隧道,从而改变隧道渗流场分布。
(4)衬砌的存在对于隧道渗流量有重要的影响,隧道渗流量随衬砌渗透性的降低迅速减小后趋于平缓。衬砌的存在能够削弱渗透各向异性比n对隧道渗流量的影响,且衬砌渗透性越低,削弱能力越强,不同n下的隧道渗流量差异越小。软黏土等弱透水土体的渗透各向异性对隧道渗流量的影响更大,在此情况下考虑土体渗透各向异性对于隧道渗流量的影响更有意义。
(5)隧道渗流量随地表压力水头线性增加,且不同渗透各向异性比下隧道渗流量之间的差值也随着地表压力水头增加而增加,渗透各向异性对于隧道渗流量的准确反映在地表高水位下更应值得关注。
限于篇幅,本文未分析注浆圈对于渗透各向异性下不同衬砌渗水模式隧道渗流量的影响,将在下一步详细研究注浆圈的厚度、渗透性对于隧道渗流量的影响。
