基于ADS-B数据的一次雷达系统误差配准方法
2024-02-23张召悦黄诚昊
张召悦, 黄诚昊
(中国民航大学空中交通管理学院,天津,300300)
一次雷达和广播式自动相关监视系统(automatic dependent surveillance broadcast, ADS-B)是空中监视的主要手段,两者对目标监视原理不同,ADS-B只能监视合作目标,而雷达可实现合作与非合作目标的全空域监视。虽然在民航领域一次雷达已逐渐被二次雷达和ADS-B所替代,但在军用领域及航空进近区域依旧是主要的监视手段。大部分一次雷达在出厂前会进行系统误差的配准,但雷达的系统误差会随着时间的推移而累积[1],长时间使用后需再次进行系统误差配准。因此研发一套高效的一次雷达系统误差配准方法具有重要的现实意义。
当前主要的标校方案包括静态有源标校方案与动态标校方案,前者采用信标机进行标校,其操作复杂且成本较高。后者以靶标(航空器)为合作目标,在靶标(航空器)上加装差分全球定位系统(differential global position system , DGPS)以提升航空器的定位精度,并记录DGPS的定位数据作为标校真值。该方法存在诸多不利因素,如调度靶标受航线、空域限制,导致校准周期长、花费成本高、实施难度大等。
在国际民航组织(international civil aviation organization , ICAO)的推动下,多数民航飞机均已装备ADS-B IN/OUT设备并实时广播本机的位置等参数,这些信息来自机载全球卫星导航系统(global navigation satellite system , GNSS),可靠稳定、易于选取[2],精度一般是普通雷达的3倍以上,可间接或直接作为真值来配准雷达系统误差[3-4]。
当前雷达系统误差的配准研究主要集中在2个方向:①基于雷达系统误差在空间中分布均匀假设下的常值函数配准方法,如最大似然配准[5-6]、最小平方准则[7]、基于傅里叶变换的方法[8]、实时质量控制法[9]等;②基于雷达系统误差在空间中分布不均匀假设下的配准方法,如曲面网格逼近方法[10]、拟合分区配准[11]、基于数据驱动的配准方法[12]等。上述方法大多忽略了随机误差对雷达系统误差配准的影响[13],将整体误差直接进行误差分析与配准工作,对A/C模式的二次雷达配准十分有效。但是一次雷达配准时,由于存在较大的随机误差及轨迹刚性偏转现象,传统方法无法有效提升雷达监视精度。对此研究人员引入了卡尔曼滤波算法来减小随机误差并进行系统误差配准,但传统卡尔曼滤波算法通常需要加入偏置函数来抵消雷达系统误差,偏置函数的精确性就决定了雷达系统误差的配准精度。
针对上述问题,本文基于雷达系统误差在空间中分布均匀的假设下提出了一种基于点云的跟踪滤波配准方法。
1 航迹点时空对准方法
1.1 监视数据坐标转化
卡尔曼滤波作为线性滤波器,需要在笛卡尔坐标系下进行计算。因此需将极坐标系(azimuth elevation range, AER)中的雷达航迹数据与空间大地坐标系(geographic coordinate system, GEO)中的ADS-B航迹数据转化到同一空间直角坐标系(earth centered earth fixed , ECEF)中。
1.2 航迹点时空对准
因一次雷达数据缺少关键的航班号信息,无法直接进行系统误差配准研究,需将雷达航迹与对应的ADS-B航迹相关联。如果两条航迹在一定时间内有足够多的航迹点可被中心点聚类算法划分为同一簇,则这两条航迹表征的是同一个目标。基于此原理,提出了一种基于中心点聚类的航迹关联方法,该方法以航空器航迹点的时间戳和航空器飞行高度为粗筛选条件:
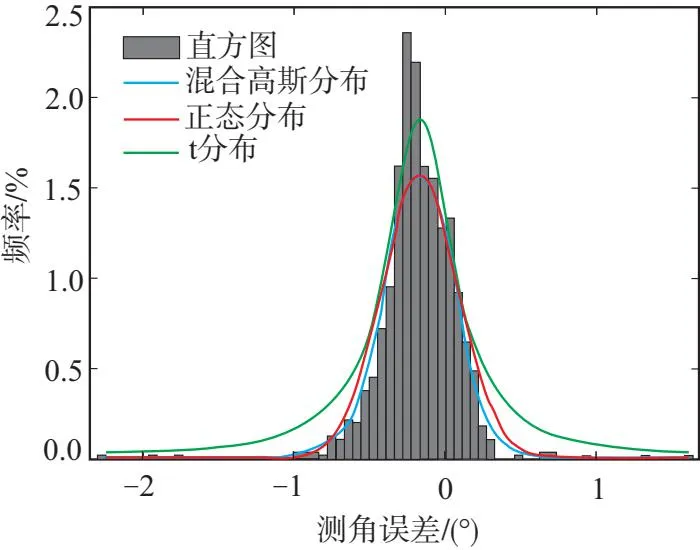
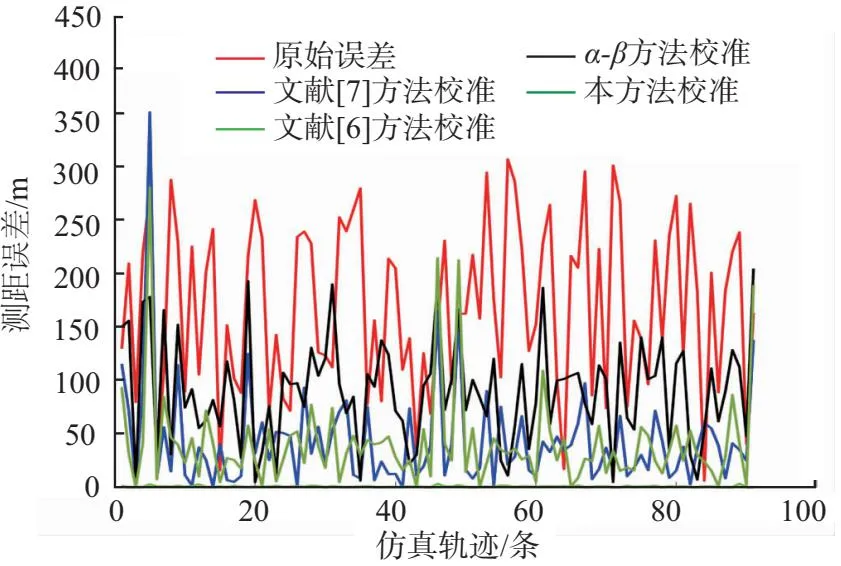
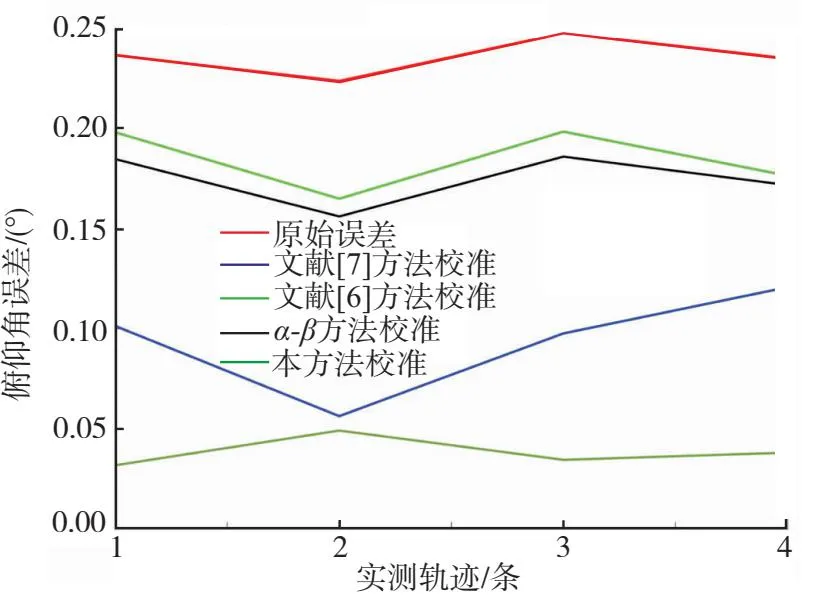
步骤 1对将要进行中心点聚类的航迹点进行粗筛选,以雷达设备的扫描周期tperiod为筛选范围,雷达航迹点高度与ADS-B航迹点高度的差值阈值为Hlim。假设选取的雷达航迹点时间戳为Tr,其对应的高度为Hr,ADS-B航迹点的时间戳为Ta,i,其对应的高度为Ha,i。筛选ADS-B航迹点集中时间戳满足|Tr-Ta,i| 步骤 2采用中心点聚类算法,将步骤1通过粗筛选的所有ADS-B和雷达目标点进行聚类。在K-means算法中,异常航迹点将对算法产生较大影响,因而选取K-Medoids方法作为ADS-B和雷达航迹点的航迹关联算法。 将雷达与ADS-B航迹点的集合作为中心点聚类算法的输入,以不同ADS-B航班号的数量K作为输出,使每个航迹点与其所属簇的中心航迹点距离总和最小。随机选择K个航迹点作为初始中心点,反复用其他航迹点(非中心点)代替中心航迹点,直至迭代至最优的中心航迹点。 对迭代完成的K个航迹点簇进行分析,判断Tr时刻该雷达点归属的航迹簇,并检验该簇中ADS-B航迹点是否都属于同一个航班号,若检验结果为真,则将该雷达航迹点与对应的ADS-B航迹形成关联关系。 步骤 3引入航迹关联百分比(track match percentage,TMP)概念,如果某一时刻Tr,第i条雷达航迹的航迹点和第j条ADS-B航迹的航迹点可被中心点聚类算法分为同一簇,则第i条雷达航迹中存入1个第j条ADS-B航迹的航班号,一段时间内求出第i条雷达航迹中存入的各个航班号的占比即为TMP,TMP(i,j)=max{TMP(i,n),n=1,2,…,n}。当TMP(i,j)≥85%时,则认为第j条ADS-B航迹与第i条雷达航迹为关联状态。 步骤 4由于雷达数据和ADS-B数据更新周期不同,对雷达系统误差分析时,应将两者的航迹数据进行时间戳同步,获得相同时刻标度下的航迹数据。由于ADS-B数据的更新频率约为雷达数据更新频率的2~4倍,因此以雷达数据的时间戳为基准,对ADS-B的航迹数据进行插值,完成航迹数据的时间戳同步。3次样条插值法的插值次数较低,待定系数易求解,插值速度较快,且在局部拟合中插值函数的光滑性较好,故选择该方法[14]。 雷达数据和ADS-B数据进行时空对准后,将ADS-B航迹数据转化至以雷达为中心的极坐标系中,计算雷达与ADS-B数据的测角误差(误差统计为直方图)。对测角误差直方图进行分析,结果见图1。测角的整体误差(随机误差+系统误差)并不呈现为正态分布,文献[15]发现该误差服从某一自由度的t分布。但整体贴合度依旧不高,因此结合雷达系统误差和随机误差的混合影响因素,考虑采用混合高斯分布模型反映直方图的特征: (1) 式中:N(μk,Σk)为正态分布;αk为混合高斯分布的权值;K为单高斯模型数量。在图1中可以看出,混合高斯分布模型对雷达测角误差直方图有较好的拟合效果。整体误差呈现混合高斯分布,反映出雷达误差存在多个误差源,传统的配准方法忽略了随机误差而重点考虑系统误差的方法,在大误差一次雷达的配准研究中并不适用。 图1 测角误差分布拟合图 将误差源分离,并对不同误差源采用不同的配准方法较为合理,因此本文提出了一种改进的轨迹跟踪滤波配准方法。轨迹跟踪滤波算法可减小大误差一次雷达测量过程中随机误差对修正雷达系统误差的影响,减小雷达航迹中因随机误差而产生的航迹波动,而点云配准算法则可预先计算轨迹跟踪滤波算法中的偏置函数或补偿函数,进而提升跟踪滤波算法在进行雷达配准时系统误差的配准精度。 为确定卡尔曼滤波算法进行误差配准时最优偏置函数,本文将点云配准算法中的迭代最近点法(iterative closest point,ICP)引入卡尔曼滤波算法中,ICP算法通过不断迭代寻找雷达观测数据与ADS-B参考数据之间最小平均误差的刚性变换矩阵,从而获得最优的偏置函数。 为避免因位姿初始值选择不当导致ICP算法陷入局部最优的情况,引入随机抽样一致性算法(random sample consensus,RANSAC)进行粗匹配。RANSAC算法通过不断选择随机点对,并记录最优的匹配点对集合,获得可靠的变换矩阵作为ICP算法中的位姿初始值。 基于点云配准算法获得偏置函数主要分为5步:①确定一段历史数据中的雷达航迹点(待配准点云)与ADS-B航迹点(基准点云);②确定RANSAC算法的迭代次数、两点的阈值距离、内点的占比,采用RANSAC算法将雷达航迹与ADS-B航迹进行粗配准,输出初始变换矩阵;③将RANSAC粗配准后输出的变换矩阵作为ICP算法的初始值,ICP配准中通过K-D树查找雷达航迹与ADS-B航迹之间的对应点,并迭代求解目标函数;④最终输出ICP精配准后的位姿变换矩阵,将得到的位姿变换矩阵作为粗偏置函数;⑤将一段历史数据中所有的ADS-B航迹与雷达航迹按上述方法求解粗偏置函数,并存入集合,利用遗传算法求解偏置函数集合中最优的偏置函数。 在进行机动目标跟踪滤波时,为快速适应机动目标,需实时切换不同的运动模型,然而单模型的运动模式是固定的,不具备实时调整的可能性,因此使用固定结构交互式多模型算法时,建立多个模型并存储在模型集合中,每个模型代表一种飞机的运动模式。为了保证跟踪模型可以更加匹配机动目标,需要在模型集合中储存大量飞机运动模型,然而这势必会导致跟踪精度的降低[16]。 因此,需选取变结构交互式多模型算法来对雷达探测目标进行跟踪滤波,减少随机误差带来的影响。该算法的关键在于能够动态地调整模型的结构和参数,以适应目标在不同模式之间跳变的情况。因此,本文采用基于期望增加模型的变结构交互式多模型算法(expected-mode augmentation for multiple-model estimation,EMA),来抑制雷达航迹中的随机误差。 假设飞机运动模型集为M,通过扩展期望模型,找到更好的描述目标运动状态的运动模型C,使得模型集E=M∪C,模型E称为期望模型集。一般模型集Mk是随着时刻的变化而变化的,通过应用模型自适应算法,新的模型集为:Mk=Ek∪(Mk-1-Ek-1),Mk为k时刻的模型集,Ek为k时刻的扩展期望模型集,Mk-1为k-1时刻的模型集,Ek-1为k-1时刻的扩展期望模型集。 模型集自适应分为两部分,第一部分为模型之间的切换,模型切换过程中假设M中各模型之间的相互转换服从齐次的马尔科夫过程;第二部分为期望模型扩展,期望模型扩展将生成一个新的期望模型来代替原有的期望模型。 模型集自适应步骤如下: 步骤1计算有效模型的模型概率和似然函数。 (3) (6) 步骤3卡尔曼滤波。 将RANSAC-ICP点云配准获得的最优偏置函数b,代入单一模块的Kalman滤波器中。 x(k)=Fx(k-1)+b+w(k-1) (7) 式中:x(k)为系统的状态向量;F为状态转移方程;b为偏置函数;w(k-1)为过程噪声。 为验证上述算法的性能,本文进行了仿真实验和实测验证。图2为雷达误差配准的流程图。 图2 雷达误差配准流程图 为验证本算法的可靠性,采用计算机仿真的方法对本文文献[6]、文献[7]和Alpha-beta滤波器的算法进行对比。ADS-B数据源于华东某地区的实测数据,雷达仿真数据通过ADS-B航迹数据增加刚性偏移量产生。为保证实验的可靠性,建立2组仿真场景,分析算法的性能。 3.1.1 场景 1:二次雷达A/C模式的监视场景 X方向添加系统误差200 m,Y方向添加系统误差200 m,Z方向添加系统误差400 m。X、Y、Z方向分别添加均值为50 m的高斯噪声。图3为该场景的仿真结果。 (a)配准结果 (b)方位角误差 (c)俯仰角误差 (d)测距误差 3.1.2 场景 2:大误差一次雷达的监视场景 X方向添加系统误差200 m,Y方向添加系统误差200 m,Z方向添加系统误差400 m。X方向添加均值为50 m的高斯噪声,Y方向添加均值为100 m的高斯噪声,Z方向添加均值为100 m的高斯噪声。添加随机生成的旋转误差0.2°~0.3°。图4为该场景的仿真结果。 各方法计算效率分别为:文献[6]为0.20 s,文献[7]为2.08 s,α-β滤波为0.035 s,本方法1.88 s。此处的计算时间为处理约90条轨迹所花费的时间。 在场景1的仿真结果中,4种配准方法在配准的精度上都具有较好的表现,尤其是文献[6]、文献[7]中的方法,在对A/C模式二次雷达的配准中,都具有较高的配准精度。本文提出的方法在测距精度上略低于前2种方法,但在测角精度上具有较好的配准效果。 (a)配准结果 (b)方位角误差 (c)俯仰角误差 (d)测距误差 在场景2的仿真结果中,文献[6]、文献[7]和Alpha-beta滤波器在配准的精度上均有降低,尤其是文献[6]中的方法因其不具备滤波器功能,在出现大误差场景时精度出现大幅度降低。文献[7]中的方法在大误差的场景下,精度也出现了降低,主要归因于大误差的场景往往伴随着雷达轨迹出现刚性偏转,对刚性偏转无法较好的配准。本文提出的配准方法能在大误差的场景下依旧保持较高且稳定的配准精度,主要得益于卡尔曼滤波器中偏置矩阵的优化与卡尔曼滤波器本身对于噪声轨迹的优化。 在运算时间效能上,Alpha-beta滤波的方法在测距精度上稍弱于其他3种配准方法,但在运算时间效能上,Alpha-beta滤波器作为一种构造简单的滤波器,在时间性能上大幅度领先于其他方法,更加适合于工程应用。文献[7]的方法大部分时间用于实时计算变换矩阵H,而本文提出的方法通过历史轨迹数据率先进行了最优偏置矩阵的计算,因此本文提出的方法比文献[7]方法花费的时间短。 本次实测使用的雷达精度参考标准如下:方位角精度为0.3°,测高误差为800 m,测距误差为60 m,是一种大误差的一次雷达。该雷达测角误差较大,且探测的目标距离在100 km左右,因此俯仰角度的轻微误差都会导致几百米的测高误差。 本实验首先对该雷达的历史数据进行分析,利用RANSAC-ICP算法获得卡尔曼滤波算法的最优偏置函数,同时复现文献[6]、文献[7]、α-β滤波器的雷达配准算法与本算法作对比。其中文献[7]采用了一种实时动态的卡尔曼滤波算法,采用变换矩阵H来进行偏置或状态补偿。文献[6]采用了最大似然估计来进行雷达系统误差的配准。Alpha-beta滤波器计算效率高,是一种偏向工程的配准方法。图5为某一时段的实测雷达数据配准结果。 (a)实测配准结果 (b)测距精度 (c)俯仰角精度 (d)方位角误差修正结果 在俯仰角的配准中,不具备滤波器功能的文献[6]与滤波性能较低的α-β滤波器配准结果并不理想。这是因为该雷达的大误差主要反映在俯仰角测量精度较低,导致俯仰角噪声和随机误差较大。而基于卡尔曼滤波算法的2类方法都保持了理想的配准结果,其归因于卡尔曼滤波算法对于随机误差具有较好的抑制作用。 在方位角的配准中,本文方法与文献[7]方法相比,具有更好的配准精度,这是因为文献[7]中获得的变换矩阵H来自同一时段下周围航空器的航迹偏移数据,该小数据量的估计方法,提升了配准方法的实时性,但牺牲了配准方法的准确性。本文方法一部分基于文献[7]的思想,利用卡尔曼滤波降低随机误差对雷达配准的影响,同时又对此算法提出改进,提前对雷达的历史数据进行分析,借助点云配准思想来确定最优的偏置矩阵,在配准过程中实时性与准确性都优于传统卡尔曼滤波算法。 对该型号雷达收到的大量雷达航迹实验验证的结果见表1。处理效率为每处理100条轨迹所花费的时间。 实测分析符合雷达精度的参考标准。从表1中可以得出α-β滤波器虽然计算速度最快,但同时也损失了一部分精度作为代价。文献[6]的优势在于不需要历史数据做支撑,可直接投入雷达配准的应用中,但在大误差一次雷达的配准中修正精度和修正速度均低于本文的方法。文献[8]的修正方法在修正波动较小的方位角时,修正效果较好,且计算速度较快,但因不具备滤波器功能,在波动较大的俯仰角修正时,得不到较好的修正结果。通过本文提出的方法修正后该雷达俯仰角精度提升至0.04°,方位角精度提升至0.07°,相较于文献[7]、文献[6]和α-β滤波器的方法,精度得到较好的提升。同时与同类型的文献[7]方法相比,具有较高的计算效率。因此本文提出的方法在配准大误差一次雷达时,具备更好的配准效果。 表1 各方法修正精度结果对比 针对一次雷达系统误差配准问题,本文首先采用中心点聚类对雷达数据和ADS-B数据进行航迹匹配,其次分析雷达误差的分布特征,发现雷达误差呈现混合高斯分布的特性,验证了雷达误差由多种误差源构成。同时针对传统卡尔曼滤波配准方法忽略了偏置函数或补偿函数的问题,本文提出了改进EMA-IMM的配准方法。该方法利用RANSAC-ICP算法来确定最佳的卡尔曼滤波偏置函数或补偿函数。研究结果表明,该算法可以提高大误差一次雷达监视定位的精度,具有实际的工程应用价值。后续的研究将集中于ADS-B数据的精度分析,以满足高精度雷达标定需求。1.3 雷达误差分布模型
2 改进的雷达轨迹跟踪配准算法
2.1 偏置函数的确定
2.2 跟踪滤波算法
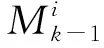

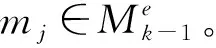

3 算例分析

3.1 仿真验证



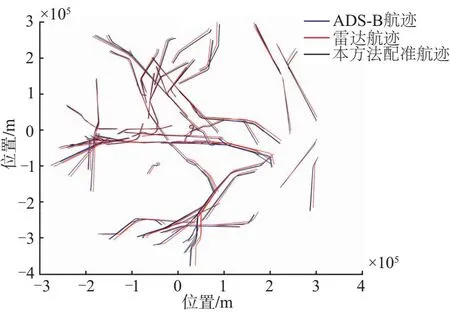
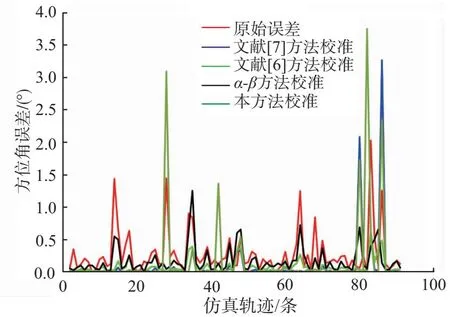

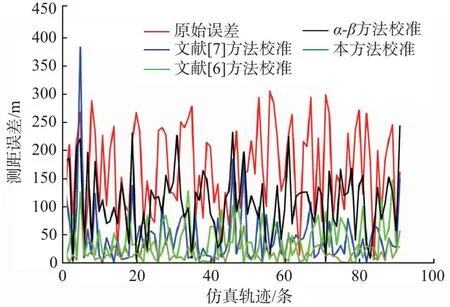
3.2 实测分析

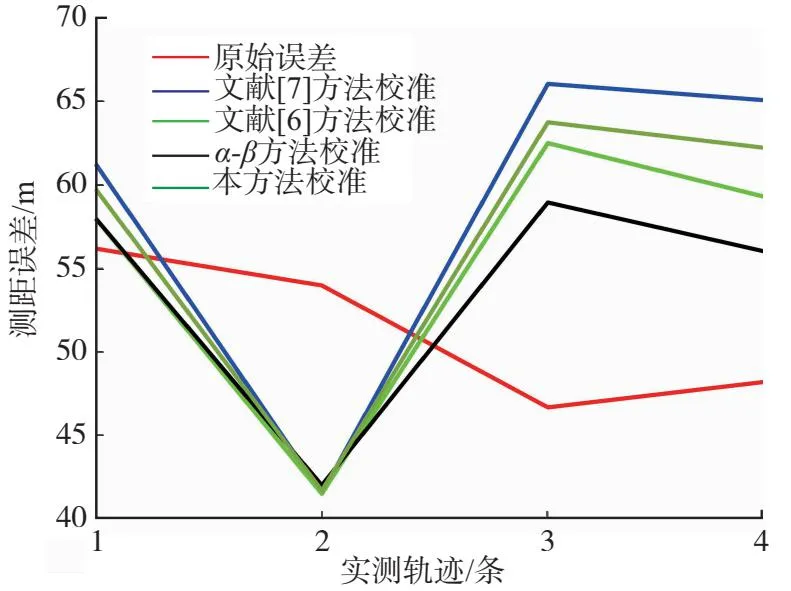

3.3 结果分析

4 结语
