由Hadamard卷积定义的一类广义解析函数的系数估计研究

敖 恩,李书海,程晓亮

(1.赤峰学院 数学与计算机科学学院,内蒙古 赤峰 024000;2.赤峰学院 民族数学教育研究所,内蒙古 赤峰 024000;3.吉林师范大学 数学与计算机学院,吉林 四平 136000)

1 预备知识

用A表示由在单位圆盘U={z∈:|z|<1}内解析且具有形式的函数形成的函数族.记S表示A内在单位圆盘U={z∈:|z|<1}内单叶解析函数的全体.用P表示在U内解析且形如同时满足Re{p(z)}>0的函数全体,称其为正实部函数.另外,用Φ表示P内满足条件ψ(0)=0,ψ′(0)>0和ψ(U)为关于实轴对称的区域,且形如的函数全体.

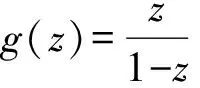
(f*g)(z)=(g*f)(z)=f(z).

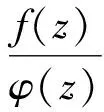
f(z)=φ(z)h(ω(z)),z∈U,

则称函数f(z)在U内拟从属于h(z),记为f(z)qh(z).特别地,当φ(z)=1时,f(z)=h(ω(z)),z∈U,称函数f(z)在U内从属于函数h(z),记为f(z)h(z);当ω(z)=z时,f(z)=ψ(z)h(z),z∈U,称函数f(z)在U内优于函数h(z),记为f(z)≪h(z).因此从属关系和优化关系是拟从属关系的两种特殊情形.

本文利用拟从属关系和Hadamard卷积引入下面的函数类.

则称f(z)∈Mq(γ,λ;g,ψ),其中γ∈{0},0≤λ≤1,ψ∈Φ.

函数类Mq(γ,λ;g,ψ)是一个更具有广义性和一般性的解析函数类.一方面,在定义1中函数g(z)或参数γ,λ取一些特殊值时,可得到若干个解析函数子类.例如:

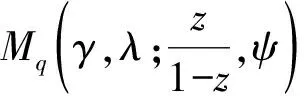
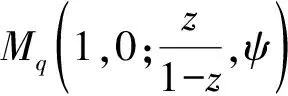
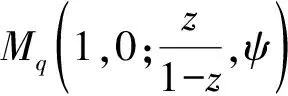
另一方面,当把拟从属替换其特殊情形—从属关系时,也可推出一些经典函数子类.例如,文献[5]中的函数类Nλ(g,γ;ψ);文献[6]中的Ma-Minda型星象函数S*(ψ)类和Ma-Minda型凸象函数类C(ψ).最后,把定义中的Hadamard卷积取为一些常见的微分算子或积分算子(例如Dziok-Srivastava算子、Carlson-Shaffer算子、Ruscheweyh算子、Bernardi-Libera-Livingston算子等)时也可得到出一些较为一般的解析函数子类.

近些年来,研究者通过拟从属关系引进了一些解析函数子类,并讨论了系数估计和Fekete-Szegö问题,如文献[2-4,7-11].受前期研究成果启发,本文利用复分析中的基本不等式和正实部解析函数系数估计,研究了新定义的广义解析函数类Mq(γ,λ;g,ψ)的系数估计上界问题,丰富了已有的相关成果.为了讨论函数类的系数估计,需要引入下面的引理.

引理1[12]设φ(z)=c0+c1z+c2z2+…在单叶圆盘U内解析且|φ(z)|≤1,则

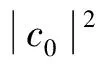
引理2[13]设ω(z)=ω1z+ω2z2+…在单叶圆盘U内解析且|ω(z)|<1,则|ω1|≤1,且对任意复数t,有

当函数ω(z)=z2或ω(z)=z时上式等号成立.

引理3[14]设ω(z)=ω1z+ω2z2+…在单叶圆盘U内解析且|ω(z)|<1,则对任意实数t有

同时,当-1

2 主要结果

除特别声明,本文规定下列函数的级数展开式分别为如下形式:

f(z)=z+a2z2+a3z3+…,

(1)

g(z)=z+b2z2+b3z3+…,bi∈,bi>0(i=2,3,…),

(2)

φ(z)=c0+c1z+c2z2+…,|φ(z)|<1,

(3)

ψ(z)=1+B1z+B2z2+…,B1∈,B1>0,

(4)

ω(z)=ω1z+ω2z2+…,|ω(z)|<1.

(5)

定理1设f(z)∈Mq(γ,λ;g,ψ),则

(6)

且对任何复数μ有

(7)

极值函数f(z)满足

或

证明由于f(z)∈Mq(γ,λ;g,ψ),则根据定义1,存在满足条件|φ(z)|≤1,ω(0)=0,|ω(z)|<1的两个解析函数φ(z),ω(z)使得

(8)

(9)

又将函数φ(z),ψ(z)和ω(z)的幂级数展开式(3)—(5)代入式(8)右侧,整理可得

(10)

把式(9)—(10)分别代入式(8)两侧,比较两边同次幂的系数可得

(11)

由此可得

(12)

于是在式(11)中利用引理1可知式(6)成立.同理,在式(12)中利用引理1和引理2便可推出式(7).即定理1证毕.

定理2若f(z)∈Mq(γ,λ;g,ψ),则对任何实数μ,有:

(1)当γc0>0时,有

(13)

(2)当γc0<0时,有

其中

(14)

证明下面对γc0>0时进行证明.根据式(7),有

其中

当μ≤σ1或者μ≥σ2时,分别有t≤-1和t≥1;当σ1≤μ≤σ2时,有-1≤t≤1.于是根据引理3可知式(13)成立.

当μ<σ1或者μ≥σ2时,对应的极值函数f(z)满足

当σ1<μ<σ2时,

当μ=σ1或者μ=σ2时,对应的极值函数f(z)分别满足

和

当γc0<0时,同理可证相应结果.综上所述,定理2证毕.

类似于定理2的证明,利用引理3也可得定理3.

定理3若f(z)∈Mq(γ,λ;g,ψ),则对任何实数μ及γc0>0,有:

(1)当σ1<λ≤σ3时,

(2)当σ3≤λ<σ2时,

又对任何实数μ及γc0<0,有

(3)当σ2<λ≤σ3时,

(4)当σ3≤λ<σ1时,

其中σ1,σ2由式(14)确定,

注在定理1—3中,令ψ(z)=1,即为文献[5]中的定理1—3.

3 结语

本文由拟从属关系和Hadamard卷积定义了比较广义的解析函数子类Mq(γ,λ;g,ψ),拓展了解析函数类范畴,并利用复分析的一些方法和正实部解析函数的系数估计和分析技巧,重点研究了由拟从属关系和Hadamard卷积定义的解析函数子类Mq(γ,λ;g,ψ)中函数的系数估计上界问题,主要解决了起始项的系数a2和a3的边界估计问题,以及在参数取为复数和实数两种情况下的系数泛函估计—Fekete-Szegö问题,得到了全新的结果.