混合远近场太赫兹通信中波束色散分析及预编码设计

赵笑洁,郝万明,王 芳,杨守义,黄崇文

(1.郑州大学 电气与信息工程学院,河南 郑州450001;2.浙江大学 信息与电子工程学院,浙江 杭州 310027)

0 引言

电磁辐射场可以分为远场和近场区域,远场和近场之间的边界通常通过瑞利距离定义[1],瑞利距离与阵列孔径的平方成正比,与波长成反比。因此,随着未来移动通信中大规模天线和高频毫米波/太赫兹的应用,电磁波辐射的近场范围将随之扩大,导致通信模式从传统的单一远场通信向近场或混合远近场通信转变[2]。此外,为降低功耗,太赫兹大规模天线一般采用混合模拟/数字预编码结构,而模拟预编码网络中采用的移相器与频率无关,这将导致宽带太赫兹信号产生波束色散,严重影响系统性能[3]。因此,如何解决远场和近场的波束色散问题是超大规模太赫兹天线应用的关键。

目前,相关文献分别对太赫兹通信中远场和近场中的波束色散问题进行了研究。 解决波束色散的方法一般是在射频链和移相器之间插入时延器,产生与频率有关的波束。例如,文献[4-6]均提出基于时延器的混合预编码架构以克服波束色散。文献[4-5]提出的方法是针对远场波束色散,而文献[6]提出的方法则是用于克服近场波束色散。具体来说,文献[4]提出了一种新的预编码架构,即延迟相位预编码,利用时延器产生与频率相关的波束使得多载波波束全部指向用户方向,提高了用户波束增益。文献[5]提出了两种混合宽带波束形成方法,即基于虚拟子阵列和基于实时延时器,前者是通过将整个阵列划分为几个虚拟子阵列来形成在整个频带上均匀分布的阵列增益的模拟波束,但是由于移相器的窄带特性,并不能完全消除波束色散;后者引入了时延器,通过在时域中为不同的天线提供额外的延迟以解决波束色散,其性能接近最优。文献[6]研究了近场波束色散问题,提出一种分段远场模型将整个大阵列划分为多个子阵列,以分段线性的方式高精度地近似近场模型。因此,可近似认为接收器位于小型子阵列的远场区域,但位于整个大型阵列的近场区域中。提出了一种相位延迟聚焦方法,即在每个子阵列的移相器和射频链之间插入时延器,通过时延器和移相器的联合作用来匹配分段远场信道模型,将整个带宽上的波束聚焦在用户期望的位置上,有效解决了波束色散问题。

当前文献均单独研究远场或者近场场景下的波束色散问题,并未联合进行研究。考虑混合远近场场景下的波束色散问题,设计了基于时延器的混合预编码天线结构,并对其性能进行分析。而后,提出一种混合场预编码设计方案,有效克服了混合远近场中的波束色散。

1 系统模型

混合远近场太赫兹通信系统模型如图1所示,基站最侧边的天线位于x、y轴的零点处,假设该模型包含一个近场用户和一个远场用户,基站采用稀疏射频(Radio Frequency, RF)链天线结构,射频数目等于用户数目。当用户与基站的距离小于瑞利距离,该用户为近场用户;当用户与基站的距离大于瑞利距离,该用户则属于远场用户[7]。瑞利距离一般用Z=2D2/λ表示[1],其中D和λ分别表示阵列孔径和载波波长。此外,为了克服频率选择性衰落[8],采用正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)传输技术,用fm表示第m个子载波的频率,fm可以表示为：

图1 混合远近场太赫兹通信系统模型Fig.1 Mixed far-and near-field terahertz communication system model

(1)

式中：m=1,2,…,M;B表示带宽,M表示子载波个数;fc为载波频率。频率fm处的波长为λm=c/fm,波数为km=2πfm/c,相对频率可设为ξm=fm/fc。

1.1 远场信道模型

基站和远场用户的信道可以表示为：

(2)

式中：N为天线的数量,hf为基站和用户之间的复信道增益,a(ψ)为远场转向矢量。

(3)

式中：ψ=2dfsinφ/c为远场用户的空间角,φ为远场用户的物理方向,d=λc/2为相邻天线间距,λc为中心频率fc的波长。

1.2 近场信道模型

基站和近场用户的信道可以表示为：

(4)

式中：gm=c/4πfmr为自由空间路径损耗,b(θ,r)为近场转向矢量。

(5)

式中：r(n)表示第n根天线与近场用户之间的距离,

(6)

式中：n=0,1,…,N-1;r0为基站参考天线与用户之间的距离,θ为近场用户的物理方向。

1.3 混合远近场下的信号模型

一般来讲,基站需要配备NRF≥NU个射频链去保证多用户通信,其中NU为用户的数量,假设NRF=NU=2。每个射频链连接一个子阵列,由两个射频链连接的两个子阵列分别向近场用户和远场用户发送信号。A表示N×NRF维模拟预编码矩阵,A=diag[an,af],其中an和af分别表示N/2×1维近场和远场的模拟预编码向量。D表示NRF×K维数字预编码矩阵,D=[dn,df],其中dn和df分别表示NRF×1维近场和远场的数字预编码向量。sn和sf分别表示发送给近场用户和远场用户的信号矢量,则近场用户和远场用户接收到的信号可分别表示为：

(7)

(8)

2 混合远近场的波束色散分析

对于宽带太赫兹下的稀疏射频链天线系统,不同频率下产生的波束方向不同,称为波束色散效应[4],这种效应将导致明显的阵列增益损失。具体而言,在远场场景中,波束色散效应将导致不同频率的波束扩展到不同方向[9-11]。在近场场景中,波束色散效应将导致不同频率的波束聚焦在不同方向和不同距离[6,12]。远场和近场波束色散效应的示意图如图2所示[6],图中每个子图中都包含了最低频率、中心频率和最高频率的波束能量,说明了物理空间中的归一化阵列增益。图2(a)～(b)分别是窄带时没有波束色散的远场波束和近场波束,可以看出,当没有波束色散时,远场的波束指向同一方向,近场的波束聚焦在同一位置上。图2(c)～(d)分别是宽带时的出现波束色散的远场波束和近场波束,可以看出,当存在波束色散时,远场不同频率的波束指向不同的方向,近场不同频率的波束聚焦在不同位置上。

(a) 远场窄带波束

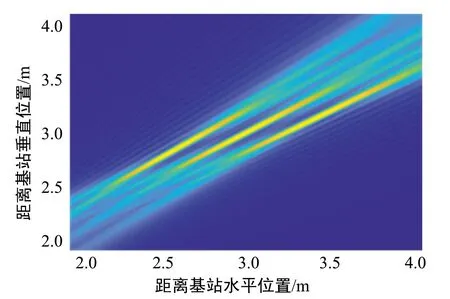
(d) 近场波束分裂

2.1 远场波束色散

在远场宽带通信中,由于太赫兹超宽带宽,不同频率波束的物理方向与目标偏差显著增加。而且,太赫兹大规模多入多出系统中天线数量的增多将导致波束宽度变窄。因此,不同频率的波束在不同物理方向上将会完全分离[6],导致非常严重的阵列增益损失。具体分析如下[13]：

设中心频率fc产生的波束方向为φc,频率fm产生的波束方向为φm,且fm=fc+Δf,其中,Δf为频率fm偏离中心频率fc的程度。移相器产生的相移为φc=2πfcdsinφc/c,这是频率为fc时产生的相移,由于移相器是频率无关的,则相移值不随频率的变化而改变。当频率为fm时,相移为φm=2πfmdsinφm/c。在窄带通信时,fm≈fc,故可得φm≈φc,因此窄带通信时不同频率的波束基本都指向相同的位置,此时可近似认为窄带系统中没有波束色散现象。然而在宽带系统中,频率fm不能再近似等于中心频率fc,由公式φc=φm可以得到频率fm产生的波束方向为：

(9)

式中：频率fm越远离中心频率fc,波束的偏移越严重。在宽带通信时,由于带宽很大,子载波频率远离中心频率,因此子载波产生的波束都远离中心频率产生的波束,这将导致严重的波束色散现象,会极大地影响通信系统的性能。

2.2 近场波束色散

在近场宽带通信场景中,波束色散的表现形式与远场不同,近场中的波束不仅有角度信息,还有距离信息,因此波束色散会导致波束聚焦在不同的位置上,即近场的波束色散不仅会导致波束指向不同的方向,而且还会使波束聚焦的距离发生改变。具体分析如下[14]。

由菲涅尔近似[15]和二阶泰勒级数展开可得,第n根天线与近场用户之间的距离为：

(10)

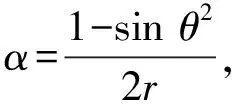
(11)

(12)

(13)

3 基于时延器的混合远近场波束设计

在传统的混合预编码架构中引入时延器网络,即在射频链和移相器网络之间加入新的时延网络,架构如图3所示。具体而言,假设加入K个延时器,每个射频链链连接Ksub=K/2个时延器,每个时延器以子连接的方式连接P个移相器,因此每个射频链连接Nsub=N/2个天线元件。时延器网络可以通过时间延迟实现与频率相关的相移,例如相移-2πfmt可以通过子载波频率fm处的时间延迟t来实现[4]。

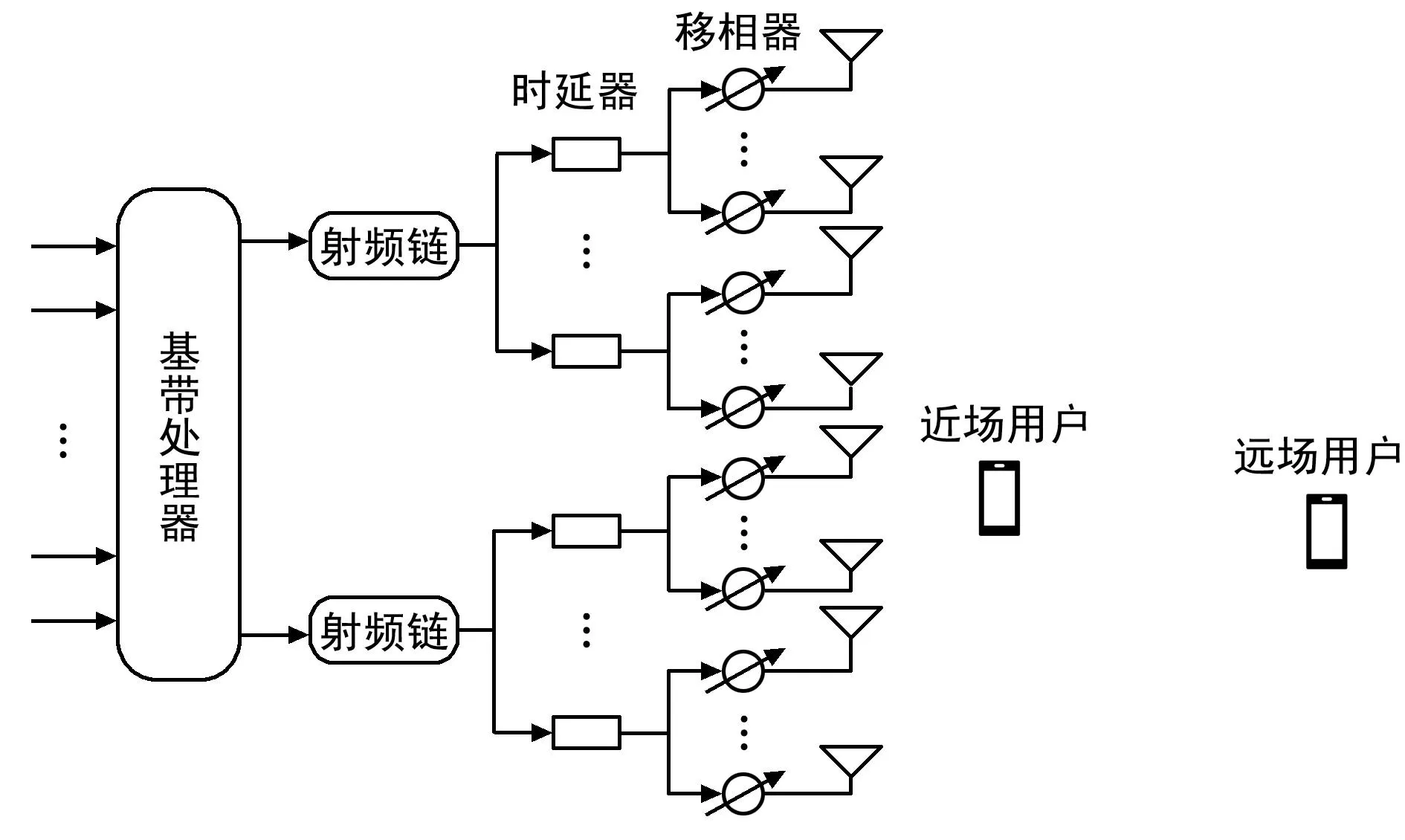
图3 基于时延器的混合预编码架构Fig.3 Hybrid precoding architecture based on time delay

3.1 远场延迟相位预编码

为了缓解远场波束色散带来的阵列增益损失,在远场使用一种称为延迟相位预编码[4]的预编码架构来解决这个问题。当波束的频率为fm时,相邻两个时延器所在的子阵列的相移差为πPψm,其中远场在频率fm的空间角为ψm=2dfmsinφ/c。当频率为fm时,假设相邻两个时延器的相移差为πβm,相邻两个时延器所在的子阵列里对应位置的移相器产生的相移差为πPψc,其中ψc=2dfcsinφ/c。则由以上分析可以得出：

πPψm=πβm+πPψc,

(14)

式中：βm=(ξm-1)Psinφ为方向旋转因子。

因为βm∈[-1,1],即-1≤(ξm-1)Psinφ≤1,又因为sinφ∈[-1,1]且f1/fc≤ξm≤fM/fc,故P≤1/(fM/fc-1),将K=N/P带入其中,可得延时器的数量应满足K≥(fM/fc-1)N。

分析移相器产生的相移,假设移相器在第k个子阵列上产生的1×P维模拟预编码向量为wk,则有下列表达式：

[w1,w2,…,wKsub]H=aT(ψc),

(15)

式中：ψc=2dfcsinφ/c,a(ψc)中的N=Nsub。

分析时延器产生的相移,假设第k个时延器产生的与频率有关的相移为-2πfmtk,为了保证波束与远场用户的物理方向对齐,时间延迟tk应该是中心频率fc周期的整数倍,即1×Ksub维时间延迟向量为：

t=[0,sTc,2sTc,…,(Ksub-1)sTc]。

(16)

式中：Tc为中心频率fc的倒数,s表示波束延迟的周期数,且需要满足：

-2πfmsTc+2πs=πβm。

(17)

由于πβm的范围是[-π,π],因此加上2πs是为了保证公式左边的相位在这个范围之内,从而解得：

(18)

式中：s与每个子阵列的移相器数量P和远场用户的物理角度φ有关,与相对频率ξm无关,这意味着时间延迟可以补偿子载波处的波束色散。考虑到s是一个常数,且时间延迟tk应该大于0,优化后第k个时延器的时间延迟可以写为：

(19)

故时间延迟向量可写为t=[t0,t1,...,tKsub-1]。

由以上分析可得,对于引入时延器的预编码架构,Nsub×1维远场模拟预编码向量可以写为：

af=[e-2πfmtdiag(w1,w2,…,wKsub)]T。

(20)

3.2 近场相位延迟聚焦

由于近场的波束色散效应,大部分子载波将遭受很严重的阵列增益损失,为了解决这一问题,可在近场使用一种称为相位延迟聚焦[6]的方法。用分段远场模型来近似近场信道,在此基础上,使用相位延迟聚焦方法来减轻波束色散效应。

由式(10)可以看出近场的相位kmr(n)相对于n是非线性的。当天线数量较少时,可以采用平面波假设下的远场模型,此时相位kmr(n)≈km(r0-ndsinθ)是线性的,并且天线数量越少,这种线性近似越精确。由于近场的相位kmr(n)相对于n是非线性的,因此直接去设计近场宽带波束形成比较困难,解决方法是使用一个分段远场信道模型来近似近场信道,具体模型示意图如图4所示。在这个模型中,用时延器把整个阵列划分为多个子阵列,使每个子阵列的天线数量远小于整个阵列的天线数量。对于每个子阵列来说,由于天线数量变少,近场范围也显著减小,因此,虽然用户位于整个阵列的近场区域,但是也可以认为用户位于每个子阵列的远场区域,所以可以参考远场解决波束色散的方法来解决近场的波束色散问题。

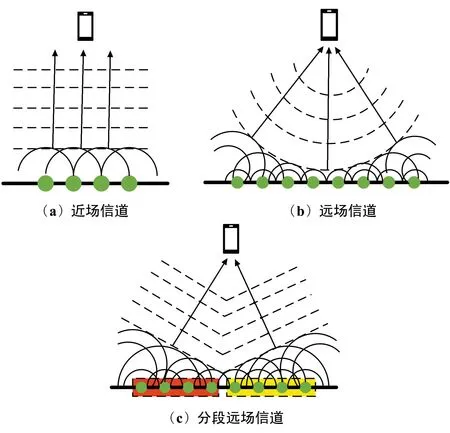
图4 信道模型的示意图Fig.4 Schematic diagram of channel model

将近场信道模型重新排列可以写为：

hn=gm[h(0),h(1),…,h(Ksub-1)],

(21)

式中：1×P维向量h(k)是第k个子阵列与近场用户之间的子信道。第k个子阵列的参考天线与近场用户的距离和角度分别为：

(22)

(23)

式中：k=0,1,…,Ksub。

第k个子阵列中的第p根天线与近场用户之间的距离可以写为：

rk-pdsinθk。

(24)

(25)

分段远场信道模型的相位可以精确地近似于近场信道的相位,所使用的信道模型可以视为对现有近场信道模型的分段线性化,即在每个子阵列中相位相对于n是线性的。利用这种分段线性相位特性,接下来使用一种称为相位延迟聚焦的近场宽带波束聚焦方法来缓解近场波束色散效应。

基于上面提出的分段远场通道模型,信道中的相位可以分为两部分：第一部分是不同子阵列间的近场信道相位-kmrk,第二部分是每个子阵列内的远场信道相位kmpdsinθk=πpsinθk,这两部分都会导致近场波束色散效应。然而,当天线数量较少时,波束色散引起的性能损失可以忽略不计[4],由于子阵列中天线的数量远小于整个阵列中天线数量,可以推断出远场信道相位πpsinθk对近场波束色散的影响很小,因此主要任务是补偿近场信道相位-kmrk来缓解不同子阵列之间的近场波束色散效应。信道相位-kmrk=-2πfmrk/c在频率fm处是线性的,可以通过时间延迟rk/c来补偿,因此在射频链和移相器之间插入时延器,时延器在频率fm处的频率响应为e-j2πfmr′/c=e-jkmr′,其中r′是可调节距离参数,如果r′=-rk,时延器能够补偿频率相关的相位-kmrk。另外,移相器生成的频率无关的相移能够补偿每个子阵列内的远场相位πpsinθk。通过移相器和时延器的共同作用,整个带宽上的波束能量近似聚焦在近场用户所在的位置上,以上方法就是相位延迟聚焦(Phase-Delay Focusing,PDF)法。

假设移相器在第k个子阵列上产生的1×P维模拟预编码向量为vk,通过以上分析可以得到Nsub×1维近场模拟预编码向量：

(26)

式中：vk由一个时延器和P个移相器生成。

(27)

3.3 基于时延器的混合预编码设计

近场用户和远场用户的干扰信噪比(Signal to Interference plus Noise Ratio,SINR)可以分别表示为：

(28)

(29)

因此,相应的速率表达式如下：

Rn=lb(1+SINRn),

(30)

Rf=lb(1+SINRf),

(31)

故可实现和速率表示为：

(32)

4 仿真结果与分析

表1 仿真参数

图5展示了不同带宽和不同混合预编码架构下,系统的可实现和速率与子载波的关系。在基于时延器的混合预编码架构下,令时延器数目K=32,在基于移相器的混合预编码架构下,令带宽B=0.3、3.0、30.0 GHz,在这几种情况下,分别计算出不同子载波时系统的可实现和速率。由图5可以看出,随着带宽的增大,波束色散效应越来越严重,传统的混合预编码架构由于波束色散效应而遭受的性能损失也越来越大,而基于时延器的混合预编码架构可以弥补大部分的性能损失。此外还可以看出,当fm≈fc时,所有情况下的可实现和速率都与理想情况下的可实现和速率相等,此时可认为没有波束色散。本文理想情况是没有波束色散。

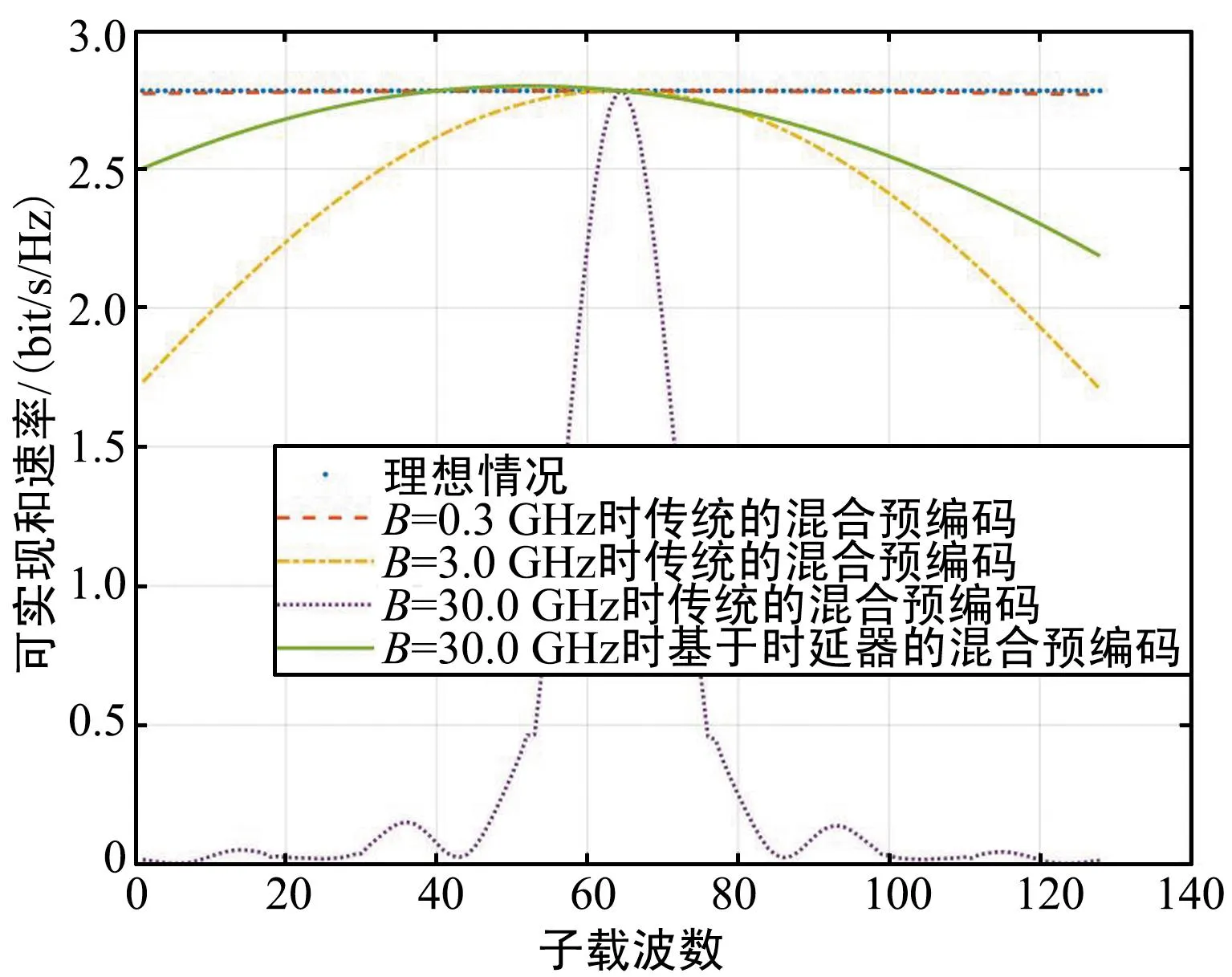
图5 和速率与子载波的关系图Fig.5 Relationship diagram between rate and subcarrier

图6展示了不同混合预编码架构下,系统的平均可实现和速率与信噪比(Sighal to Noise Ratio, SNR)的关系,其中时延器数目K=32。假设ρn=ρf=ρ,由于数字预编码矩阵使用的是ZF预编码,故：

图6 平均可实现和速率与SNR的关系图Fig.6 Relationship diagram between achievable rate and SNR

(33)

(34)

定义传输SNR为ρ/σ2。由图6可以看出,基于时延器的混合预编码结构的性能接近理想性能,而传统的混合预编码结构的性能损失严重,并且随着SNR的增大,性能损失越来越严重,因此引入时延器可以大大缓解波束色散导致的系统性能损失。

图7展示了基于时延器的混合预编码架构的平均可实现和速率与时延器数目的关系,可以看出,理想情况和传统的混合预编码结构的平均可实现和速率不发生改变,因为这两种情况都不包含时延器。此外与理想情况相比,传统的混合预编码结构性能损失严重。对基于时延器的混合预编码来说,系统的平均可实现和速率随着时延器数目的增加而增加,并且逐渐接近理想情况下的平均可实现和速率。由此可以得出,时延器的数目越多,补偿波束色散的效果也越好。

图7 平均可实现和速率与时延器数的关系图Fig.7 Relationship diagram between achievable rate and the number of time delayers

图8展示了不同混合预编码架构下的平均可实现和速率与天线数目的关系,其中时延器数目K=16,可以看出,随着基站天线数目的增多,除了理想情况,其他情况下的性能都遭受了损失。但是基于时延器的混合预编码架构的性能损失要小于传统的混合预编码架构的性能损失,并且当天线数目比较少的时候,基于时延器的混合预编码架构的性能接近于理想情况下系统的性能。这种情况出现是因为当天线数目比较少时,时延器的数量可以满足缓解波束色散的要求,然而随着天线数目的增加,时延器数目不能满足补偿波束色散的要求,此时需要增加时延器的数目才能有效减轻波束色散带来的性能损失。

图8 平均可实现和速率与天线数的关系图Fig.8 Relationship diagram between achievable rate and the number of antennas

5 结论

本文研究了超宽带太赫兹通信系统中的波束色散问题,并提出了混合远近场下基于子阵列的混合预编码架构。为了缓解波束色散效应,在传统的混合预编码结构中引入时延器,对引入时延器后的子阵列结构进行混合预编码设计以克服波束色散。此外,还对传统的混合预编码架构和基于时延器的混合预编码架构的性能进行比较和分析。仿真结果表明,大带宽和大天线数量导致的波束色散会使传统的混合预编码架构在性能方面出现严重的损失,在射频链和移相器之间插入时延器就会大大缓解波束色散带来的性能损失。