硬件集合通信中聚合树构建方法
2024-02-20陈淑平尉红梅何王全漆锋滨
陈淑平 尉红梅 王 飞 李 祎 何王全 漆锋滨
(国家并行计算机工程技术研究中心 北京 100190)
目前超级计算机已经迈入E 级计算时代,但随着摩尔定律接近失效、颠覆性使能技术迟迟不能实现,超级计算机在访存、通信、能耗等方面仍面临严重的发展瓶颈[1]. 而MPI(message passing interface)集合通信[2]是高性能计算中最重要的通信类型,对整机系统的性能具有重要的影响,提升MPI 集合通信性能是突破通信墙的重要手段. 传统的MPI 集合通信是基于点到点消息实现的[3-4],随着系统规模的不断扩大,这种实现方式面临越来越严重的性能及可扩展性问题,而硬件集合通信具有性能高、可扩展性好等优点,正受到越来越多的关注[5].
硬件集合通信中,数据沿聚合树进行规约或广播操作,聚合树的高度、负载均衡性等对集合操作的性能具有至关重要的影响. 本文研究了影响硬件集合通信性能的因素,提出了硬件集合通信开销模型,并以此为基础提出了构建硬件集合通信聚合树的方法. 本文主要贡献包括4 个方面:
1) 提出了硬件集合通信开销模型,能够较精确地计算硬件集合通信的时间开销;
2) 研究了如何根据消息大小确定聚合树的宽度,从而在网络传输开销与数据计算开销之间取得平衡,以降低集合操作的延迟;
3) 针对Ⅰ型聚合树,提出了最小高度分层k项聚合树构建方法,相比传统的Ⅰ型聚合树,降低了跨组聚合包的个数,减少了网络拥塞;
4) 针对Ⅱ型聚合树,提出了最小代价Ⅱ型聚合树构建方法,减少了聚合树使用的交换机数量.
1 研究背景
1.1 硬件集合通信简介
近年来,网络计算技术发展迅速[6-7]. 网络计算可将数据规约计算、协议处理、数据加解密等原本由处理器承担的计算任务卸载到网络设备中进行,解放了CPU,使CPU 可以专注于其他任务的处理. 在高性能计算领域,可利用网络计算提升MPI 集合通信性能. 本文将基于网络计算实现的MPI 集合通信称为硬件集合通信. MPI 集合通信中,Barrier,Bcast,Reduce,Allreduce 是应用最广泛的操作,它们均是1对多或多对1 的通信模式,适于以硬件集合通信方式实现. 图1 显示了Allreduce 的实现过程,它利用聚合树完成数据聚合及结果分发操作,该树中叶节点对应通信进程,根节点及中间节点对应交换机. 进行集合通信时,数据先从叶节点向根节点聚合,并在聚合的过程中计算规约结果;到达根节点后再沿反方向将规约结果广播给所有叶节点. 其他集合操作的实现方式与此类似.

Fig. 1 Implementation phases of Allreduce operation based on in-network-computing图1 基于网络计算的Allreduce 操作实现过程
目前,很多公司推出了面向高性能计算的硬件集合通信技术,如IBM BlueG/Q 中的硬件集合通信原语[8-11]、Mellanox 的SHARP 技术[5,12-14]、神威互连网络中的硬件集合通信[15]等. 相较于点到点消息实现的集合通信,硬件集合通信的性能有了显著提升. Zimmer等人[16]在Summit 系统中利用基准程序对SHARP 性能进行了测试,4 096 个节点规模下集合消息性能至少提升了1 倍.
1.2 硬件集合通信使用中存在的问题
硬件集合通信除了需要特殊的硬件支持外,还需要网络管理软件的密切配合,以完成聚合树分配、多播路由配置等操作. 其中,聚合树分配是其中最为关键的操作. 现有的硬件集合通信技术在分配聚合树时还存在3 个问题:
1) 缺乏精确的集合通信开销模型,无法更好地指导聚合树构建. 基于 α- β模型的软件集合通信开销模型[3]过于简化,而针对特定网络的专用模型又不具备通用性[17],它们均不适用于硬件集合通信.
2) 构造聚合树时未考虑相互干扰问题. 当系统中存在大量通信域时,需要为每个通信域分配1 棵独立的聚合树,以降低各通信域间的相互干扰,而现有的聚合树分配方法未充分考虑到该问题. 例如,SHARP 技术中每个作业的所有通信域共享同一棵聚合树[18],这会产生严重的相互干扰. 现有的聚合树构建方法也没有考虑到同一聚合树内不同消息间的相互干扰问题. 例如,传统方法构建出的聚合树会产生较多的跨组通信,使得同一集合操作的不同消息因竞争通信链路而相互干扰.
3) 未考虑硬件通信资源不够用问题. 网络中用于支持硬件集合通信的资源是有限的,而现有的聚合树构建方法未考虑该问题,导致出现通信资源不够用的情况. 例如,BlueG/Q 中每个网络节点最多支持12 棵聚合树,在很多情况下,由于聚合树数量不足,无法使用硬件集合通信[11].
针对上述3 个问题,本文研究如何建立硬件集合通信开销模型,以及如何基于该模型高效地构建聚合树.
2 硬件集合通信开销模型
2.1 定义及假设
定义1.互连网络. 互连网络定义为有向图I=(N,L),其中N为网络节点集合,L为通信链路集合. 网络节点包括网卡及交换机. 本文假设网卡在I中均是叶节点.
定义2.聚合树. 在互连网络I=(N,L)上目标集合M(M⊂N)对应的聚合树是一棵树A=(NA,LA),M⊆NA⊆N,其中M是通信域中各进程所在的网卡集合.A中边( µ, υ)的长度定义为I中 µ到 υ的距离,也即I中从 µ到 υ经过的网络链路数.A不必是I的子树,也即不要求LA⊆L. 另外,M中允许有重复元素,从而使得每个节点上可同时运行多个通信进程. 聚合树还需满足度约束条件,也即每个节点的最大子节点数不能超过硬件阈值.
定义3.聚合树高度. 设A=(NA,LA)是互连网络I=(N,L)上目标集合M对应的一棵聚合树,A中从叶节点出发到达根节点所经过的边的最大条数,称为聚合树的高度. 只有1 个节点的聚合树高度为0.
定义4.聚合树半径. 设A=(NA,LA)是互连网络I=(N,L)上目标集合M对应的一棵聚合树,A中从叶节点出发到根节点所经过边的长度之和的最大值称为聚合树半径. 聚合树半径实际上是从各叶节点出发沿该聚合树依次经过各祖先最终到达根节点时所经过的最大链路条数.
现有的硬件集合通信技术中,有的仅支持将集合操作卸载到网卡中进行,有的则还可将集合操作卸载到交换机中进行. 根据不同的卸载位置,本文将聚合树分为Ⅰ型聚合树及Ⅱ型聚合树2 种类型.
定义5.Ⅰ型聚合树. 设A=(NA,LA)是互连网络I=(N,L)上目标集合M对应的一棵聚合树,若M=NA,则称A为Ⅰ型聚合树. 该类聚合树中,集合操作均被卸载到网卡中执行,且仅使用进程所在的那些网卡.
定义6.Ⅱ型聚合树. 设A=(NA,LA)是互连网络I=(N,L)上目标集合M对应的一棵聚合树,T=(NT,LT)是I的一棵子树,M⊆NA⊆NT⊆N,且T中叶节点均在M中. 若∀u∈NA,u在A中的父亲p也是u在T中的某个祖先,则称A为Ⅱ型聚合树. Ⅱ型聚合树中的集合操作均被卸载到交换机中进行.
图2 显示了Ⅰ型聚合树和Ⅱ型聚合树. 假设有8个进程参与集合通信,每个网卡上1 个进程,互连网络的拓扑结构如图2(a)所示;图2(b)是一棵Ⅰ型聚合树,高度为3,半径为12;图2(c)是一棵Ⅱ型聚合树.

Fig. 2 Aggregate trees of type Ⅰ and type Ⅱ图2 Ⅰ型聚合树和Ⅱ型聚合树
2.2 开销模型
本文采用式(1)~(4)所示的开销模型,模型中各变量的含义如表1 所示. 本文关注于如何降低聚合过程的开销,下面着重对聚合过程开销进行说明.

Table 1 Symbols Used in the Cost Model of Hardware Supported Collectives表1 硬件集合通信开销模型中使用的符号
Taggregate是聚合过程的时间,其包括聚合包在网络链路上的传输时间,以及在网络节点内的处理时间. 假设聚合树是k叉完全树,聚合树的半径为ratree,则聚合包在网络链路中的传输总时间为ratree×l. 设每个聚合包的匹配处理时间为 θ、存储转发时间为、规约计算时间为S*×γ,则聚合包在网络节点内的处理总时间为最终得到式(2)所示的聚合时间开销.
为进一步简化模型,除了假设聚合树是k叉完全树之外,还假设任意2 个进程之间单播路由的路径长度相等,均需经过 δ条链路,则对Ⅰ型聚合树,hatree≈logkP,ratree≈δ×logkP,从而得到式(3)所示的聚合过程开销. 而对Ⅱ型聚合树,hatree≈,ratree≈0.5δ,从而得到式(4)所示的聚合过程开销.
2.3 模型验证
本文在新一代神威超级计算机上测试了各类集合消息的延迟,并与开销模型计算出的结果进行对比. 实验环境如图3 所示.
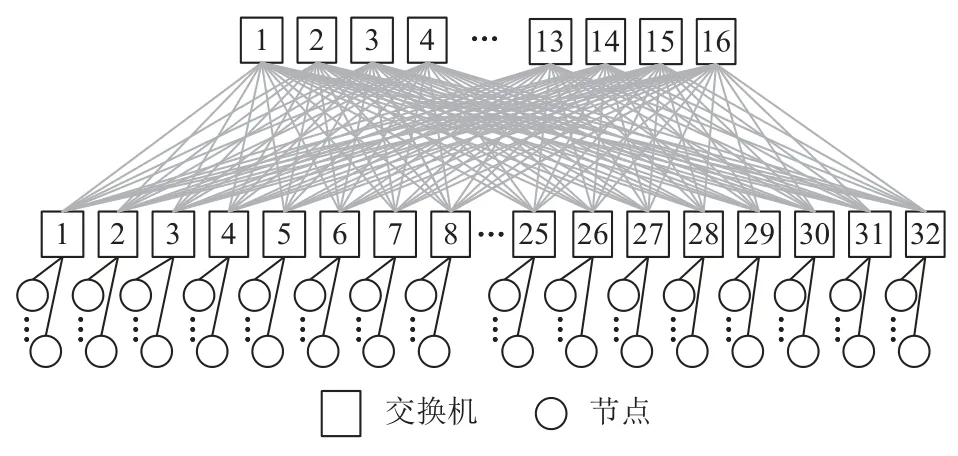
Fig. 3 2-level fat tree used in the test environment图3 测试环境使用的2 层胖树
使用1 个超节点进行测试,超节点内共有256 个节点,每个节点安装1 块消息处理芯片,每块消息处理芯片有2 个网络端口,故整个超节点内共有512 个网络端口. 这512 个网络端口通过一棵2 层胖树进行互连. 该胖树共有48 台交换机和其中32 台叶交换机和16 台骨干交换机. 每台交换机的端口数均为40,其中有些端口未被使用. 每台叶交换机有16 个端口用于连接消息处理芯片的网络接口,16 个端口用于连接骨干交换机.
分别在不同进程数下测试了各种类型、各种长度集合消息的延迟. 测试方法为:每种类型及长度均测试5 000 次,每次测试进程均记录集合操作的时间开销,取耗时最长的那个进程的时间开销作为该次集合通信的时间开销,再取这5 000 个时间开销的中位值作为当前类型、当前长度下集合消息的延迟.
限于篇幅,本文仅显示了Ⅰ型聚合树的部分测试结果. 不同进程数下,长度为8 B 的广播操作的理论计算延迟与实际测试延迟如图4 所示;进程数为512 时不同长度Bcast 消息的理论计算延迟与实际测试延迟如图5 所示. 可以看出,Ⅰ型聚合树的理论计算延迟与实际测试延迟最多相差0.5 μs. 这表明本文提出的硬件集合通信开销模型能够较准确地拟合实测延迟.
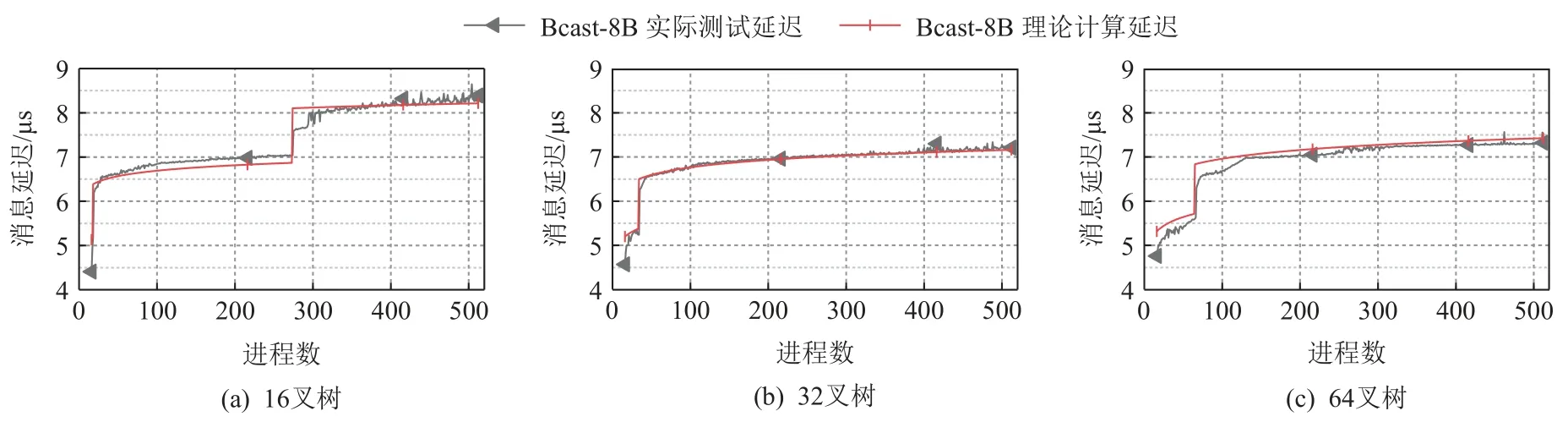
Fig. 4 Measured latency and estimated latency of collectives for different count of processes图4 不同进程数下集合操作的实测延迟及理论计算延迟
Fig. 5 Measured latency and estimated latency of collectives for different message size when process count is 512图5 进程数为512 时不同消息大小下集合消息的实测延迟及理论计算延迟
3 Ⅰ型聚合树的构建
给定任意P个进程,为它们构造一棵开销最小的Ⅰ型聚合树是非常困难的,因为不但要考虑聚合树宽度、聚合树半径等因素,还要考虑通信与通信重叠、通信与计算重叠、消息间相互干扰等因素的影响,故目前Ⅰ型聚合树均是通过启发式算法进行构造. 本节首先研究如何根据消息类型、消息长度等确定Ⅰ型聚合树的宽度k,然后研究如何快速构造一棵聚合树,使得跨组聚合包的个数尽可能地少,尽量降低消息间的相互干扰.
3.1 根据聚合包大小确定聚合树的宽度
聚合过程的时间开销包括聚合包的传输时间以及处理时间. 聚合树的宽度k对聚合过程的时间开销具有重要影响. 直观上看,如果k很小,则聚合树很高,相应地聚合包的传输开销就很大;如果k很大,则每个网卡需要处理的聚合包很多,相应地聚合包的处理开销就很大. 需要研究k对聚合时间开销的影响.
先看如何选择k才能使式(3)计算出的聚合开销F(k)最小. 记定义如式(5)所示的F(k),其导数函数如式(6)所示.
使F(k)取最小值的k记为k∗,此时的F(k)记为F∗.根据式(5)(6),要使F(k)取最小值,需F′(k)=0,也即k(lnk−1)=,而函数f(k)=k(lnk−1)是单调递增的.对不同的集合操作类型及消息长度,取值不同,使F(k)取最小值的k也不同. 在本文的实验环境中,对同步、广播操作来说,k= 41 时F(k)取最小值.
很多情况下,选择其他k值时,F(k)与F∗差别不大. 以同步、广播操作为例,在本文的实验环境中,设P= 512,a= 1.12 μs,b= 0.01 μs,F(k)的曲线如图6所示,可以看出,当24 ≤k≤64时,F(k)相差不大,不超过0.1 μs. 对每种类型、每种长度的集合消息,都可以确定区间[kmin,kmax], 使得∀k∈[kmin,kmax]时,|F(k)−F∗|≤ε成立( ε是常数). 本文测试环境中使用的k如表2 所示(仅显示了部分结果). 可以发现,随着聚合包长度增大,kmin及kmax均逐渐下降. 对该现象的直观解释是:当聚合包长度较小时,聚合包在网络链路上的传输时间在总聚合时间中占比最大,此时应该采用较大的k,从而使得聚合包在网络链路上的传输尽量并行;而当聚合包长度较大时,聚合包在网卡内的处理时间在总聚合时间中占比最大,此时应采用较小的k,以使更多的网卡参与聚合包的处理.

Table 2 Type Ⅰ Aggregate Tree Breadth Used in the Test Environment表2 测试环境中使用的Ⅰ型聚合树宽度

Fig. 6 Curve of F(k) for Barrier and Bcast operation图6 同步、广播操作的F(k)曲线
3.2 传统的聚合树构建方法
确定k值后就可以构建聚合树了. 式(3)假设任意2 个进程间的单播路由经过的链路数相等,但实际情况要复杂得多. 使用相同的k值构造的2 棵聚合树值半径ratree可能不同,导致聚合包的传输开销不同.带度约束的最小半径聚合树问题是NP 难的[19-21],尚未有高效的求解办法. 本文目标不是构造最优聚合树,而是快速构造出一棵满足度约束条件、半径尽可能小、冲突尽可能少的聚合树. 本节首先介绍2 种传统的聚合树构建方法.
3.2.1k叉树
定义7.k叉树.k叉树是一棵完全树,除最后一个中间节点外,根节点及其他中间节点都有k个子节点,故k叉树是平衡树,每个中间节点处理的聚合包个数相等.
在k叉树中,按广度优先遍历方式为进程编号,根进程编号为0. 若进程在通信域内的编号为my_rank,则其父节点编号为(my_rank−1)/k,第i个子节点编号为my_rank×k+i(i≥1).
由于未考虑网络拓扑结构,在胖树网络[22-23]、蜻蜓网络[24]等具有分组结构的网络中,k叉树会产生大量的组间通信,导致网络拥塞. 16 个进程构建聚合树,其网络拓扑如图7 (a)所示,4 叉树如图7(b)所示. 粗线表示该聚合包需要经过最顶层的交换机,图7(b)中共有8 个聚合包经过最顶层的交换机. 如果最顶层的交换机传输能力不足,则很容易在顶层交换机处形成拥塞. 而图7(c)是另一棵聚合树,其高度、半径均与图7(b)所示聚合树一样,但仅有2 个经过顶层交换机的聚合包,因而具有更优的性能.
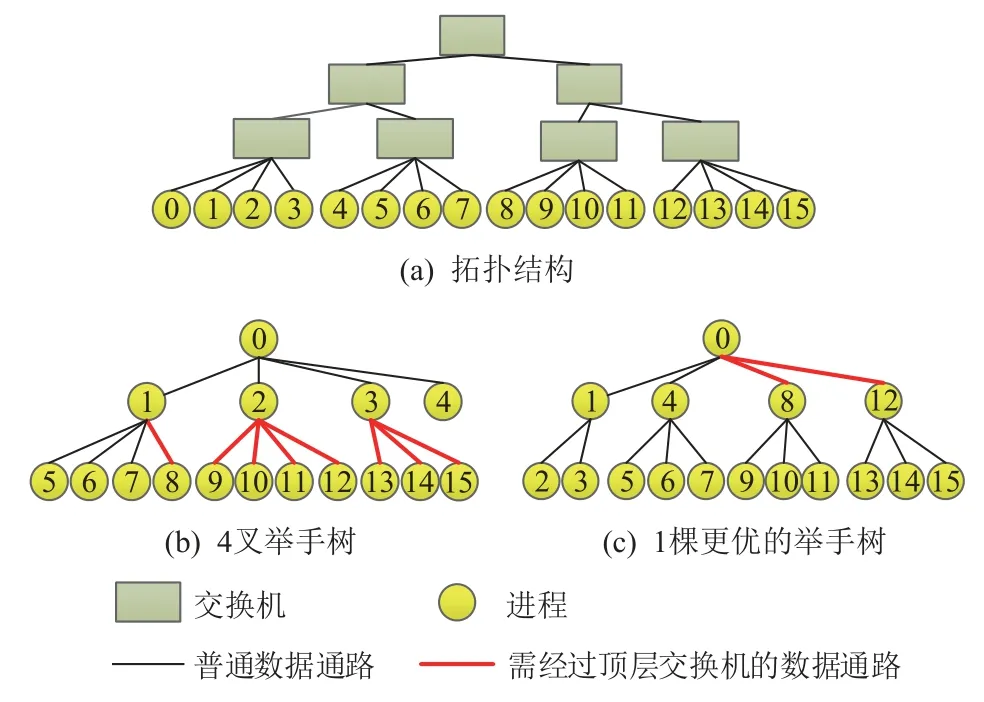
Fig. 7 k-ary aggregate tree is prone to generate lots of intergroup communication图7 k 叉树易产生大量的组间通信
3.2.2k项树
定义8.k项树.k项树[25]是一组递归定义的树Tn,其中T0是1 个单节点的树;而Tn是由k棵Tn−1连接起来构成的树,其中k−1 棵Tn−1的根节点直接连接到另外那棵Tn−1的根节点上.k项树第i层的节点数是(k−1)i×,节点总数是kn,高度为n.
图8 分别显示了一棵2 项树及一棵4 项树. 2 项树是特殊的k项树,在软件集合通信中已得到了广泛使用,例如在MPICH 中短的Bcast、Reduce 均是通过2 项树实现的[3];而大于2 的k项树目前使用得较少.

Fig. 8 k-nomial tree (k=2, 4)图8 k 项树(k=2, 4)
与k叉树不同,k项树中不同深度的节点拥有不同数量的子节点,其中根节点的子节点数最多,为(k−1)×「logkP⏋;而随着深度的增加,子节点数越来越少,故k项树是非平衡树.
由于k叉树是平衡树,k叉树中上层节点要等待下层节点处理完毕之后才开始处理聚合包,故上层节点会存在空等待现象. 而k项树是非平衡树,位于不同层的节点可以并发处理聚合包,不存在空等待现象.
在k项树中,按深度优先遍历方式为进程编号.进程编号用k进制表示为kn−1···k2,k1,k0,其中最低位共有i个0(0 ≤i≤n),则第i个位置0 即可得到其父节点编号,从最低的i位中任选一位置为1,2,···,k−1,则得到其子节点的编号最多有i×(k−1)个子节点.
每个进程调用算法1 所示的build_k_nomial_tree函数计算parent_rank及children_cnt. 与k叉树一样,k项树也会产生很多跨组通信.
算法1.build_k_nomial_tree.
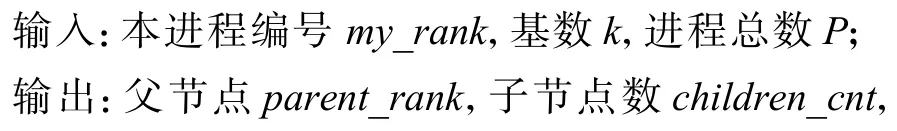
3.3 分层k 项树构建方法
传统的聚合树构建方法未考虑网络拓扑结构,容易产生较多的组间通信,从而造成网络拥塞. 为解决此问题,本文提出了分层k项树构建方法.
分层思想是优化集合通信的一种重要策略[26-29],该策略利用了不同的层具有不同数据传输性能的特点,将同一层内的进程组织成组,使尽可能多的通信在组内完成,以降低层间通信、提升集合消息性能.
在构建Ⅰ型聚合树时,利用分层思想也可以降低聚合过程的时间开销. Zhao 等人[25]提出了一种简单方法:先将进程分为不同的组,并为每个组单独构建一棵k项树;然后将各组的首进程组成一个新的组,并创建一棵k项树,从而将所有组连接起来形成一棵更大的k项树. 进行聚合操作时,同一个组内的进程会先聚合到本组的首进程,首进程再聚合到更高层的首进程,从而大大减少组间通信. 但该方法产生的k项树可能具有较大的高度. 图9 举了一个例子:通信域内共有14 个进程,依图案分属4 个不同的组.当k= 2 时,构建的聚合树如图9(a)所示,其高度为4.实际上,可以使某个组的首进程连接到另一个组的非首进程下,从而使得聚合树更加平衡,以降低聚合树的高度. 图9(b)即是一棵更优的聚合树,其高度为3. 本文的目标是在最小化组间通信的同时使聚合树高度最低.
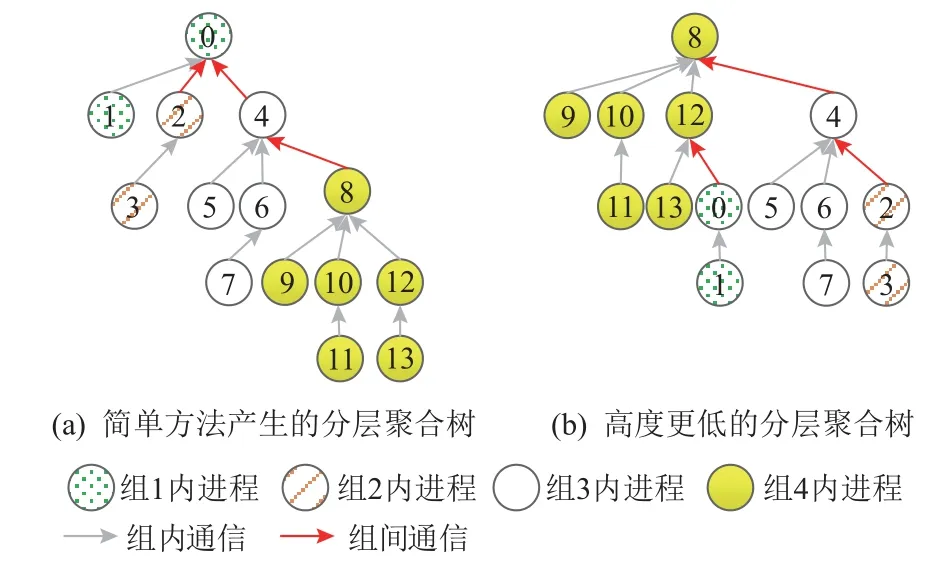
Fig. 9 Aggregate tree with hierarchical structure图9 具有分层结构的聚合树
3.3.1 问题定义
本文将具有相同通信特性的一组进程称为一个进程组. 例如,位于同一节点内的多个进程,以及位于同一交换机内的多个进程等,均可构成一个进程组. 进程组可以嵌套,从而使得一个进程组可包含多个子进程组,最终构成1 个层次结构.
进程组由如图10 所示的数据结构定义. 每个进程组都对应一棵k项树,按深度优先方式为k项树内的节点编号. 进程被映射到k项树的某个节点上,树中有些节点可能无映射进程. 该数据结构中,cnt是k项树的节点数,它必须是k的幂;ranks_id是k项树内各节点对应的进程号,nodes_id是各进程对应的k项树节点号;sub_groups定义了属于该进程组的子进程组,共有sub_grp_cnt个子进程组.

Fig. 10 The data structure of the process group图10 进程组的数据结构
下面探讨最小高度分层k项Ⅰ型聚合树问题. 给定m个互不相交的进程组g0,g1,···,gm−1,g是满足2个条件的进程组:1)g包含g0,g1,···,gm−1的所有进程;2)g对应的k项树中,除首进程外其余进程的父节点均位于gi内;3)g对应的k项树中,每个节点的儿子数不超过硬件限制. 该问题为从中找出具有最小高度的进程组g,从而为进程组g0,g1,···,gm−1构建一棵高度最小的分层k项Ⅰ型聚合树. 进程组gi(0 ≤i<m)内嵌套的子进程组也需满足条件2.
设是进程组gi首进程的进程号,根据k项树的性质,条件2 等价于且对gi内每个进程有(gi.cnt),也即进程被映射到某个编号为gi.cnt倍数的聚合树节点内,其余进程依次映射到后续节点内.
3.3.2 构建方法
给定m个进程组g0,g1,···,gm−1,且每个gi均已构建好各自的k项树之后,即完成了ranks的设置,采用算法2 为这些进程组构建一棵更大的k项聚合树. 算法2 采用贪心策略,每次找出2 个最大的进程组g0和g1,然后在g0的空闲子树内寻找能够容纳g1的位置.如果找不到这样的位置,则将g0的聚合树高度加1,即cnt变为原来的k倍,从而使g0内有足够的空余位置容纳g1. 该过程持续下去,直到最终只剩1 个进程组为止. 算法2 行⑤代码用于为g[i]寻找可用的位置,仅需检查分块的第1 个位置是否可用即可判断整个分块是否可用. 行⑫~⑭代码用于将g[i]的ranks映射表拷贝到新的聚合树中.
算法2.merge_groups.

采用数学归纳法可证明算法2 所产生的k项树是高度最小的分层k项Ⅰ型聚合树,限于篇幅,不再赘述证明过程.
算法3 以递归方式为每个层次建立进程到聚合树节点的映射关系. 算法4 根据拓扑信息建立分层的k项树.build_hierarchical_tree建立的聚合树中,每个组的进程均位于同一子树内,从而保证除该组的首进程外其余进程均向本组内的进程发送聚合包,故跨组聚合包的个数相比传统聚合树构建方法减少了. 在使用算法4 时,需要选择合适的k,以保证聚合树内每个节点的儿子数不超过硬件限制.
算法3.build_rank_mapping.

算法4.build_hierarchical_tree.

4 Ⅱ型聚合树的构建
本节研究构造Ⅱ型聚合树的方法. 构造Ⅱ型聚合树时需要综合考虑网络拓扑、进程位置等因素. 另外,在每个交换机内,每棵Ⅱ型聚合树都占用1 个聚合树条目,而硬件支持的聚合树条目是有限的,故创建Ⅱ型聚合树时,还需要考虑是否有可用的聚合树条目.
构造Ⅱ型聚合树时要考虑3 个目标:1)最小化聚合树的半径,以降低集合操作延迟;2)尽量让不同的聚合树分布到不同链路上,以降低聚合树间的相互干扰;3)使用尽可能少的聚合树条目,以支持创建更多的Ⅱ型聚合树.
本文分2 个步骤构造Ⅱ型聚合树. 1)选择1 个交换机作为树根,并构造1 棵生成树(称为物理树);2)对物理树进行裁剪,去掉不需要的交换机.
定义9.物理树. 设M是某通信域内进程所在的网卡集合,T=(NT,LT)是互连网络I=(N,L)的一棵子树,若T满足2 个条件,则称T是关于M的物理树:
1)M⊆NT;
2)T的叶节点除M中网卡之外,不包含任何其他网卡及交换机.
定义10.由物理树推导出的Ⅱ型聚合树. 设K是交换机节点的度约束函数,给定互连网络I=(N,L)上一棵关于M的物理树T=(NT,LT),由物理树T导出的Ⅱ型聚合树是满足2 个条件的树A=(NA,LA):
1)M⊆NA⊆NT;
2)若∀u∈NA,u在A中的父亲p也是u在T中的某个祖先;
3)A中每个交换机sw的子节点数不大于度约束K(sw),其中K(sw)大于sw在T中的子节点数.
实际上,由物理树T导出的Ⅱ型聚合树A可看成是将T中某些节点提升位置而得到的(仅能提升为其祖先的儿子).
定义11.Ⅱ型聚合树的代价. 设A=(NA,LA)是互连网络I=(N,L)上目标集合M对应的一棵Ⅱ型聚合树,A中交换机的个数称为该Ⅱ型聚合树的代价,记为cost(A).
4.1 选择树根并构建物理树
树根的位置决定了聚合树的半径,应该选择到通信域内各进程最大跳步数最小的交换机作为树根.
本文采用集中式方法构建物理树. 在该方法中,由集中式的网络管理软件选择树根并构建物理树.网络管理软件维护了网络的状态信息,包括交换机内空闲的聚合树条目数、网络链路的负载情况等. 网络管理软件可根据这些信息选择一个交换机作为树根.该方法具体过程为:先计算出每个交换机到通信域组内各进程的最小跳步数,据此找到所有的备选树根. 然后根据备选树根的负载情况对备选树根进行排序,优先使用负载低的树根. 选择好一个树根后,就可以构造一棵物理树,使得每个进程到树根的跳步数最少. 然后检查该物理树的每个交换机是否有空闲的聚合树条目可用. 若每个交换机都有空闲的聚合树条目,则返回该物理树;若失败,则尝试下一个树根.
4.2 构建最小代价Ⅱ型聚合树
由物理树导出的最小代价Ⅱ型聚合树问题. 给定互连网络I=(N,L)上一棵关于M的物理树T=(NT,LT)及度约束函数K,在由物理树T导出的Ⅱ型聚合树中求代价最小的聚合树A∗.
本文利用算法5 所示的函数创建最小代价Ⅱ型聚合树. 可以证明算法5 产生的聚合树A∗是由物理树T导出的最小代价Ⅱ型聚合树. 限于篇幅,证明不再赘述.
算法5.build_minimum_type_Ⅱ_tree.

图11(a)显示了一棵物理树,该树中共有16 个进程,使用了13 个交换机,每个交换机的度约束均为5;其导出的最小代价Ⅱ型聚合树如图11(b)所示,仅使用了4 个交换机.

Fig. 11 A physical tree and its reduced minimum cost type Ⅱaggregate tree图11 一棵物理树及其导出的最小代价Ⅱ型聚合树
5 在2 种聚合树中进行选择
在性能方面,Ⅰ型聚合树与Ⅱ型聚合树各有优势. 对长度较小的集合操作,聚合包的传输时间占主导,而Ⅱ型聚合树中聚合包传输路径较短,故延迟比Ⅰ型聚合树低. 对长度较大的集合操作,规约计算时间占主导,Ⅰ型聚合树可以将规约计算分布到大量网卡中并发进行,故延迟较小. 创建通信域时,需要综合考虑各方面因素,选择使用Ⅰ型聚合树还是Ⅱ型聚合树.
为简化分析,假设Ⅱ型聚合树是标准的d叉树,记则Ⅰ型、Ⅱ型聚合树的时间开销分别如式(7)(8)所示. 为简化讨论,仅考虑S′=S∗=S的情况.
定义如式(9)所示的函数F(d,k,P,S):
可以根据式(9)~(11)分析F(d,k,P,S)的变化趋势,并据此构造一张静态映射表. 给定集合操作类型及消息长度后,通过查表即可快速确定聚合树类型及宽度. 表3 列出了本文实验环境中如何根据聚合包长度来选择使用Ⅰ型聚合树还是Ⅱ型聚合树. 当申请不到创建Ⅱ型聚合树所需的通信资源时,需要回退到Ⅰ型聚合树.

Table 3 Method to Select Aggregate Tree表3 聚合树选择方法
6 性能评估
本节将在新一代神威超级计算机中对聚合树性能进行测试.
6.1 Ⅰ型聚合树性能评估
首先测试不同的Ⅰ型聚合树集合消息的延迟.对同步、广播、8B 长度的规约操作而言,选择k= 32可以获得更好的性能,故分别构造了32 叉树、32 项树、分层32 项树. 使用1 个超节点进行测试,每个节点运行2 个进程,每个进程使用1 个网络端口,这2个端口间的通信不需要经过网络链路. 分别在2 种场景下进行测试.
6.1.1 2 层标准胖树中的性能
在2 层标准胖树中进行测试. 分层32 项树使用了3 个层次,首先将位于同一节点的2 个进程组成1个组,这2 个进程间的通信不需要经过网络链路;然后将位于同一交换机内的16 个进程组成1 个组,该组内的进程通信时仅需经过2 条链路;最后将位于同一超节点内的所有进程组成1 个组,该组内的进程通信时需经过4 条链路.
图12 显示了Bcast-8B,Bcast-2KB 这2 种集合操作的测试结果. 可以看出:1)大部分情况下32 叉树、32 项树几乎具有相同的延迟;2)大部分情况下,分层32 项树的延迟低32 叉树、32 项树约0.6 μs. 分层32 项树延迟低的原因是:它先把位于同一节点内的2 个进程组成1 个组,而这2 个进程间通信不需要经过网络链路,故延迟较低. 需要指出的是,进程数较少时分层32 项树的延迟反而高于另外2 种聚合树,原因是此时的分层32 项树的高度大于32 叉树、32项树;随着进程数的增多,这3 种聚合树将具有相同的树高.

Fig. 12 Messages latency of three types of aggregate trees for different count of processes in standard fat-tree topology图12 标准胖树拓扑中不同进程数下3 种聚合树的消息延迟
不同消息长度时3 种构造方法下的聚合树的性能如图13 所示. 测试时使用了512 个进程,每个进程使用1 个网络端口. 测试结果与图12 的测试结果一致,即32 叉树和32 项树的性能相当,而分层32 项树的延迟明显低于32 叉树和32 项树.
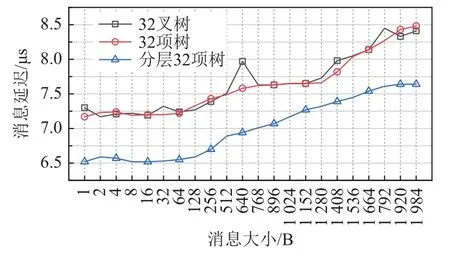
Fig. 13 Messages latency of three types of aggregate trees for different message sizes in standard fat-tree topology图13 标准胖树拓扑中不同消息长度下3 种聚合树的消息延迟
6.1.2 2 层裁剪胖树中有噪声干扰时的性能
使用如图14 所示的裁剪胖树进行测试. 该拓扑中,同一交换机内的不同网络端口向其他交换机内的网络端口发消息时会共享一条通信链路. 测试时还在网络中加入了网络噪声,该噪声消耗约80%的网络带宽.
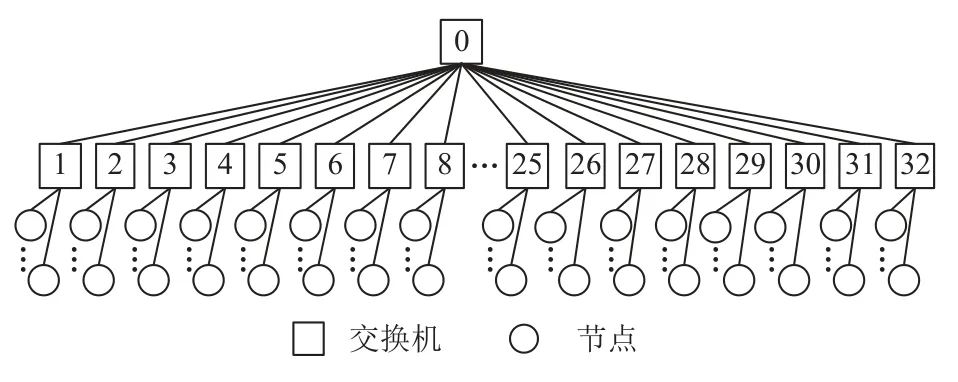
Fig. 14 Illustration of two-layer pruned fat-tree used in the test图14 测试使用的2 层裁剪胖树示意图
分别测试不同进程数时3 种方法构建的聚合树的性能,并将之与标准胖树下的测试结果进行了对比,结果如图15 所示. 可以看出,加入网络噪声后,3种构建方法的集合消息延迟相比标准胖树下有显著增大. 其中32 叉树增幅最大,分层32 项树增幅最小.
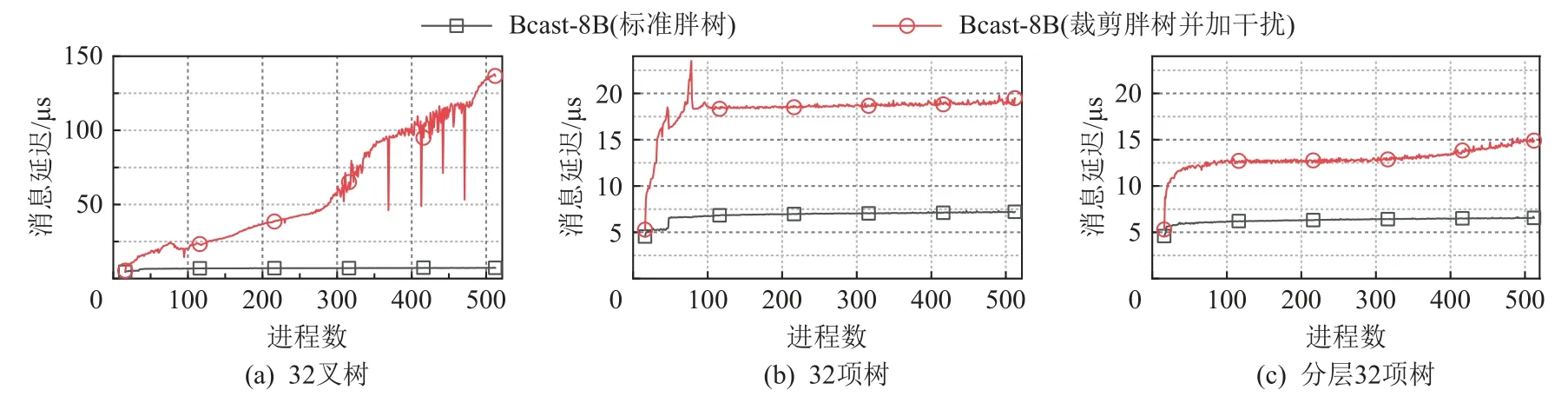
Fig. 15 Collective messages latency in pruned fat-tree topology with inference图15 裁剪胖树拓扑下有干扰时集合通信消息延迟
图16 显示了进程数为512 时,3 种方法构建的聚合树中跨组聚合包的数量,其中每条实线上的数字表示该实线所连接的2 个交换机间的聚合包个数.在32 叉树中,大量聚合包发送到1 号交换机的不同进程内,故每个集合操作中,0 号交换机与1 号交换机间链路上需传输496 个聚合包,从而产生严重的链路竞争.
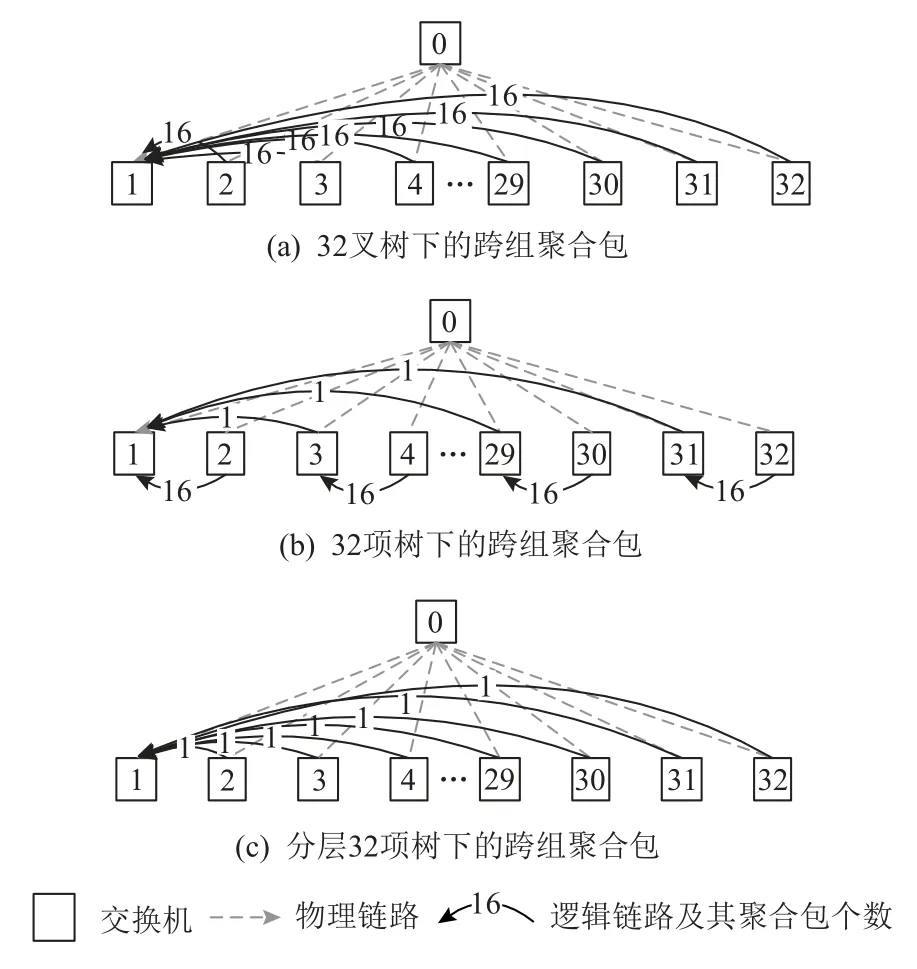
Fig. 16 Inter-group aggregation packets of three types of aggregate trees constructed methods in pruned fat-tree图16 裁剪胖树下3 种聚合树构建方法的跨组聚合包
表4 显示了不同进程数时3 种聚合树下Bcast-8 B 的延迟对比,可以看出,在存在噪声干扰的情况下,分层32 项树的延迟相比传统的聚合树构建方法下降了24%~89%. 这表明,相比另外2 种聚合树构建方法,分层32 项树具有更少的跨组聚合包,因而存在带宽竞争的情况下可以显著降低集合消息的延迟.

Table 4 Bcast-8B Latency for Different Count of Processes in Pruned Fat-tree Topology with Inference表4 裁剪胖树拓扑下有干扰时不同进程数下Bcast-8B 延迟
需要注意的是,随着进程数的增大,32 项树的延迟增加较缓慢,而分层32 项树的延迟增加略快(分层32 项树相比32 项树的延迟下降比例由进程数为64 时的32%下降为进程数为512 时的24%). 这是因为,在裁剪胖树中,随着进程数的增大,32 项树中每条链路上传输的最大聚合包数保持为16,故32 项树的延迟变化不大;而分层32 项树中每条链路上传输的最大聚合包数由1 逐渐增大到31,故分层32 项树的延迟会缓慢增加. 但可以肯定的是,随着进程数的进一步增大,分层32 项树的延迟仍低于32 项树,这是因为32 项树中每2 个相邻交换机间都需要传输16 个聚合包,从而更易受网络噪声的干扰.
除此之外,本文还在其他场景下测试了3 种聚合树构建算法的消息延迟. 例如,利用更多超节点进行了测试,其网络拓扑采用3 层裁剪胖树,故分层32 项树可采用更多的层次. 此实验的测试结论与上述测试结论一致,即分层32 项树延迟最低,32 项树次之,32 叉树延迟最高. 限于篇幅,不再赘述其详细测试数据.
6.2 Ⅱ型聚合树性能评估
6.2.1 Ⅱ型聚合树延迟测试
本节对Ⅰ型聚合树及Ⅱ型聚合树的性能进行对比. 测试环境如图17 所示. 其中Ⅰ型聚合树采用64叉树进行构建,Ⅱ型聚合树的树根建在最高层的那个交换机上. 分别测试了不同进程数下2 种类型聚合树的性能,Bcast-8 B 及Bcast-2 KB 的延迟如图18所示. 可以看出,Ⅱ型聚合树的延迟比Ⅰ型聚合树低1 μs 左右.

Fig. 17 Network topology used to compare the performance of type Ⅰ and type Ⅱ aggregate trees图17 使用网络拓扑对比Ⅰ型聚合树及Ⅱ型聚合树性能

Fig. 18 Performance comparison of type Ⅰ and type Ⅱaggregate trees图18 Ⅰ型聚合树及Ⅱ型聚合树的性能对比
6.2.2 Ⅱ型聚合树资源使用量测试
本节测试最小代价Ⅱ型聚合树构造算法的有效性以及不同通信模式下聚合树条目的使用情况.
MPI 集合通信中,一般将进程划分为2 维或3 维网格通信域,其每个维度中的每行或每列都是一个通信域. 本文测试了5 种典型的通信模式,包括2 种2 维网格结构、2 种3 维网格结构,以及1 种随机模式. 选择的2 维网格结构中,256 ×160 通信模式按拓扑结构划分通信域,模拟拓扑感知的通信模式,即第1 维有160 个通信域,故每个通信域都位于同一个超节点内;而202 ×202 通信模式存在很多跨超节点的通信域,模拟拓扑无感的通信模式. 2 种3 维网格结构也是按类似原则进行划分的. 随机模式是指进程随机加入一个通信域.
下面从2 个方面证明最小代价Ⅱ型聚合树构造算法的有效性:一方面,最小代价Ⅱ型聚合树占用的聚合树条目数相比传统方法构建的Ⅱ型聚合树有显著下降;另一方面,最小代价Ⅱ型聚合树构建算法创建聚合树时的失败率相比传统的Ⅱ型聚合树也有显著下降.
1) 聚合树占用的总条目数
首先测试每种通信模式下聚合树占用的总条目数. 假设每个交换机内的聚合树条目数足够多. 对于每种通信模式,依次为每个通信域构建Ⅱ型聚合树,并统计占用的聚合树条目总数,结果如图19 所示. 其中,传统方法构建的Ⅱ型聚合树是指利用集中式方法构建的物理树. 可以看出,所有通信模式下,最小代价Ⅱ型聚合树占用的条目总数明显低于传统方法构建的聚合树所占用的条目数,最少下降了90%. 这表明最小代价Ⅱ型聚合树算法在降低聚合条目使用量方面具有显著效果. 有些通信模式下,最小代价Ⅱ型聚合树的聚合树条目总数等于通信域个数,这是因为在这些通信模式下,每个通信域的最小代价Ⅱ型聚合树都仅使用1 个交换机.

Fig. 19 Total count of aggregate tree entries used by type Ⅱaggregate trees for different kinds of communication patterns图19 不同通信模式下Ⅱ型聚合树使用的总聚合树条目数
2)创建聚合树时的失败率
将每个交换机的聚合树条目数设为16,然后在每种通信模式下依次为每个通信域构建Ⅱ型聚合树,并记录创建失败的次数. 定义创建聚合树时的失败率为:结果如图20 所示. 可以看出,最小代价Ⅱ型聚合树算法均能为每个通信域成功构建聚合树;而传统的Ⅱ型聚合树构建方法失败率很高,最高可达74.51%.

Fig. 20 Failure rate of creating type Ⅱ aggregate trees in different communication patterns图20 不同通信模式下创建Ⅱ型聚合树的失败率
需要指出的是,将交换机的聚合树条目数设为更小的值后,某些通信模式下也存在不能创建最小代价Ⅱ型聚合树的情况,但其失败率仍低于传统的Ⅱ型聚合树构建方法,结果不再赘述.
综上所述,最小代价Ⅱ型聚合树算法可以显著减少对交换机内聚合树条目资源的占用,从而可以支持创建更多的Ⅱ型聚合树.
7 结 论
硬件集合通信中,聚合树对集合操作的性能具有重要影响. 构建聚合树时,需要综合考虑聚合树半径、宽度、负载均衡、网络噪声等的影响. 本文提出了硬件集合通信开销模型,并据此提出了3 种构建聚合树的方法,包括:1)根据聚合包大小确定Ⅰ型聚合树的宽度;2)最小高度分层Ⅰ型聚合树构建方法;3)最小代价Ⅱ型聚合树构建方法. 然后在神威互连网络中对聚合树构建方法进行了全面测试,在存在网络噪声的情况下,分层Ⅰ型聚合树的消息延迟相比传统构建方法下降了24%~89%;最小代价Ⅱ型聚合树使用的交换机聚合条目数相比传统构建方法下降了约90%.
下一步,我们将利用真实的应用程序对聚合树构建方法的性能进行更全面的测试. 另外,我们还将研究如何利用硬件集合通信提升长度较大的规约、广播等集合操作的性能,扩大硬件集合通信的适用范围.
作者贡献声明:陈淑平提出研究思路,设计算法、实验,分析实验数据并撰写论文;尉红梅指导算法及完善实验方案;王飞、李祎负责算法实现、测试数据的整理与分析;何王全、漆锋滨提出研究课题,把握论文创新性,并对论文进行修改.
