A Quasi-Linear Relationship between Planetary Outgoing Longwave Radiation and Surface Temperature in a Radiative-Convective-Transportive Climate Model of a Gray Atmosphere

Jie SUN ,Michael SECOR ,Ming CAI ,and Xiaoming HU

1Department of Earth, Ocean, and Atmospheric Science, Florida State University, Tallahassee, Florida 32304, USA

2School of Atmospheric Sciences, Sun Yat-sen University and Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519082, China

3Guangdong Province Key Laboratory for Climate Change and Natural Disaster Studies, Zhuhai 519082, China

ABSTRACT In this study,we put forward a radiative-convective-transportive energy balance model of a gray atmosphere to examine individual roles of the greenhouse effect of water vapor,vertical convection,and atmospheric poleward energy transport as well as their combined effects for a quasi-linear relationship between the outgoing longwave radiation (OLR)and surface temperature (TS).The greenhouse effect of water vapor enhances the meridional gradient of surface temperature,thereby directly contributing to a quasi-linear OLR-TS relationship.The atmospheric poleward energy transport decreases the meridional gradient of surface temperature.As a result of the poleward energy transport,tropical (high-latitude)atmosphere-surface columns emit less (more) OLR than the solar energy input at their respective locations,causing a substantial reduction of the meridional gradient of the OLR.The combined effect of reducing the meridional gradients of both OLR and surface temperature by the poleward energy transport also contributes to the quasi-linear OLR-TS relationship.Vertical convective energy transport reduces the meridional gradient of surface temperature without affecting the meridional gradient of OLR,thereby suppressing part of the reduction to the increasing rate of OLR with surface temperature by the greenhouse effect of water vapor and poleward energy transport.Because of the nature of the energy balance in the climate system,such a quasi-linear relationship is also a good approximation for the relationship between the annual-mean net downward solar energy flux at the top of the atmosphere and surface temperature.

Key words: outgoing longwave radiation,greenhouse effect,poleward energy transport

1.Introduction

It has been known that the latitudinal variation of the outgoing longwave radiation (OLR) has nearly a perfect positive linear correlation with the latitudinal variation of surface temperature since the first launch of satellites for weather and climate studies in the early 1960s (Budyko,1963).Here,for easy reference,we reproduce the quasi-linear relationship between latitudinal variations of the OLR and surface temperature using ERA5 reanalysis (European Centre for Medium-Range Weather Forecasts,Hersbach et al.,2020,https://doi.org/10.5065/P8GT-0R61).It is seen that the reanalysis dataset faithfully reproduces the original estimation for the linear fitting slope (2.08 W m-2K-1) of the quasi-linear relationship between the OLR and surface temperature reported in Budyko (1963).The estimation shown in Fig.1 is also close to the estimation (2.2 W m-2K-1) using modern satellite observations (i.e.,CERES-EBAF,v.4,Clouds and Earth’s Radiant Energy Systems-Energy Balanced and Filled)reported in (Koll and Cronin (2018,hereafter KC18).This discovery from satellite observations has led to the blooming of simple climate models.One could explore a host of scientific questions about climate sensitivity,such as the climate oscillations between glaciation initiation and retreat,multiple equilibrium states,and sudden climate changes due to hysteresis and small ice-cap instability,without using a complicated and computationally expensive radiative transfer model(Budyko,1969,1977;Sellers et al.,1969;Held and Suarez,1974;North,1975,1984;North et al.,1981,1983;Short et al.,1984).

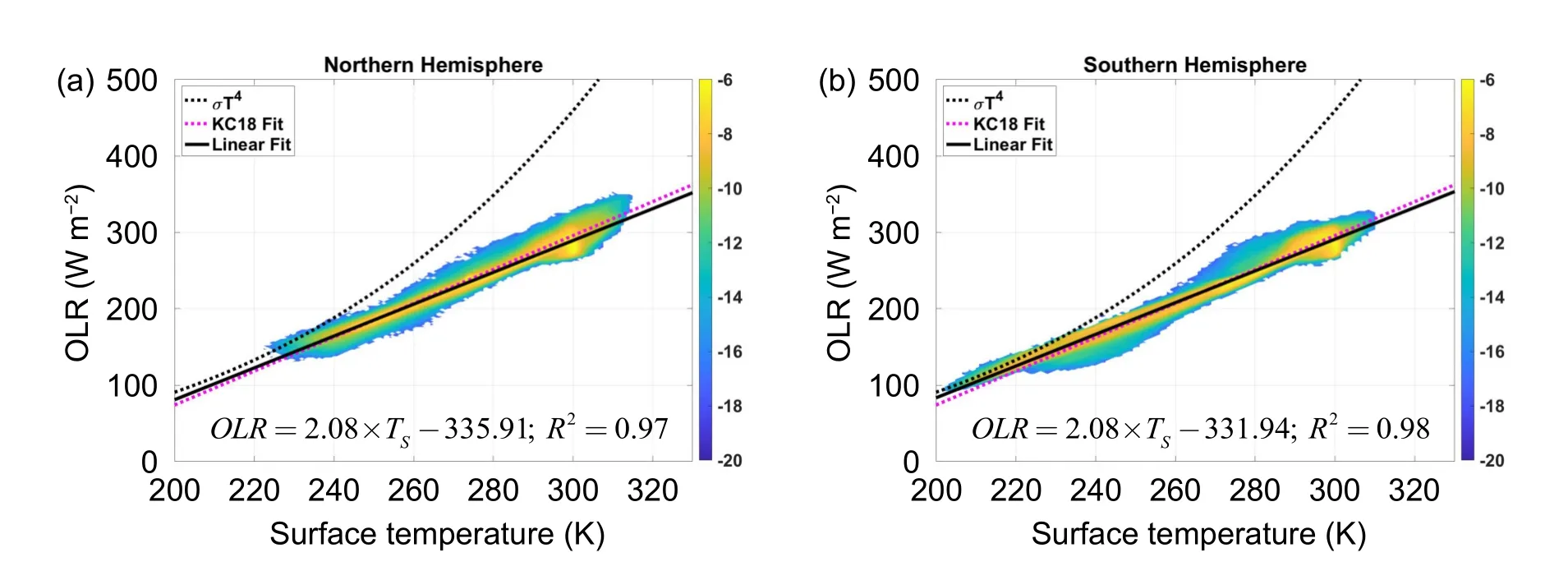
Fig.1.The Gaussian kernel density function (shadings,in logarithmic scale) for the observed relationship between the monthly-mean clear-sky OLR (ordinate in units of W m-2) and surface temperature (TS,abscissa in units of K)for the (a) Northern Hemisphere and (b) Southern Hemisphere.The total number of data points in each panel is 16 671 960,corresponding to a 1° × 1° spatial resolution covering each hemisphere for the 516 months in 1979–2021.The black solid lines are linear regression lines whose mathematical expressions and R-squared values are given in the bottom-right corner of each panel.The dashed black lines correspond to the blackbody thermal emission at TS calculated from the Stefan-Boltzmann law,and the dashed magenta curve corresponds to the straight line from the liner fitting reported in KC18.

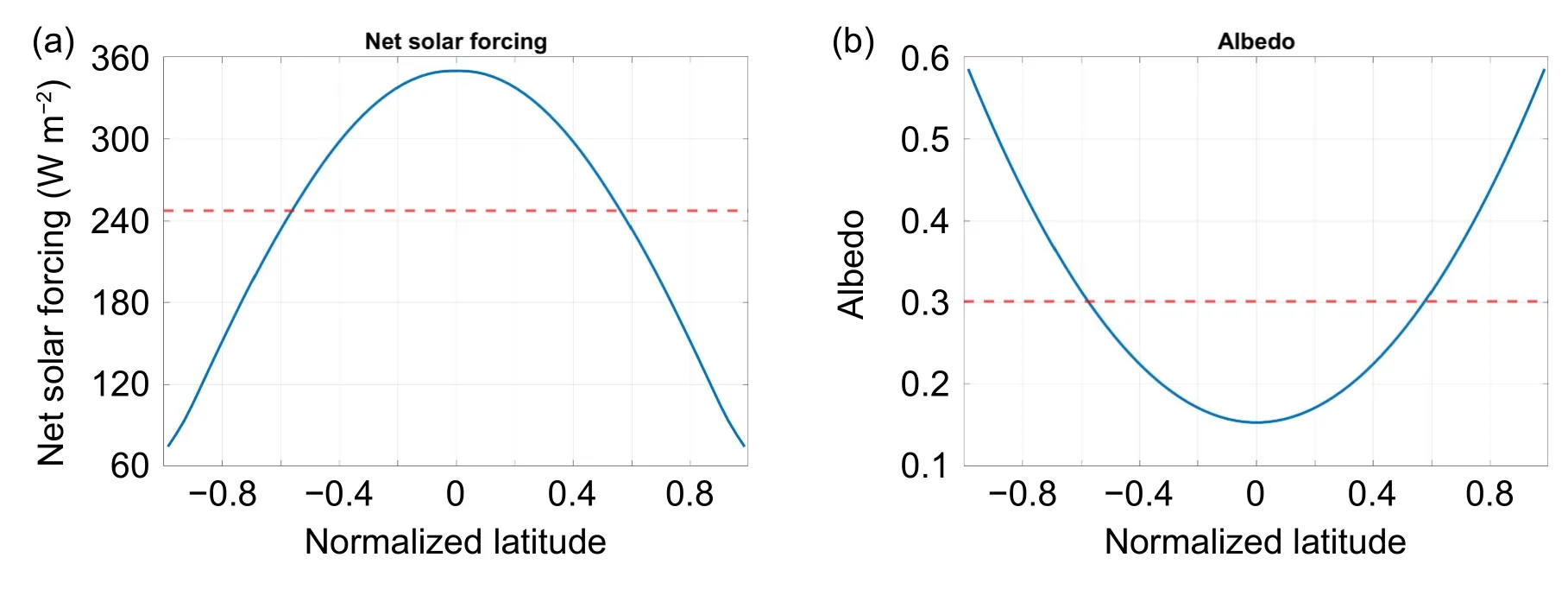
Fig.2.Latitudinal profiles of (a) the net downward solar energy flux (W m-2) at the TOA and (b) the prescribed surface albedo.The dashed thin red lines mark their global mean values.Latitudes (abscissa) are labeled as the sine of latitudes.

Because of the absorption of the upward longwave radiation (i.e.,infrared radiation) emitted by the surface by greenhouse gases such as CO2and atmospheric water vapor,a major portion of the surface’s thermal emission does not reach the top of atmosphere (TOA).Therefore,the greenhouse effect can explain why the latitudinal variation of OLR cannot be proportional to the fourth power of surface temperature (TS) per the Stefan-Boltzmann law.However,the greenhouse effect by itself does not explain the near-perfect positive linear correlation between OLR and surface temperature.Recently,KC18 reproduced the quasi-linear OLRTSrelationship by using a line-by-line radiative transfer model to calculate the OLR as a function ofTSwith prescribed vertical profiles of temperature and moisture.They attribute the quasi-linearity of the OLR-TSrelationship to the narrowing of the atmospheric window for the surface’s thermal emission to escape to space by more abundant water vapor at warm temperatures.However,Cai (2006,hereafter C06) provides evidence showing the existence of a quasi-linear OLRTSrelationship in a simple energy balance model of a gray atmosphere in which the thermal emissions of both the atmosphere and surface are explicitly expressed as the 4th power of temperatures according to the Stefan-Boltzmann law.Therefore,the quasi-linear OLR-TSrelationship could still exist without the atmospheric window for the surface’s thermal emission.

The main goal of this study is to examine the individual roles of the greenhouse effect of water vapor,vertical convection,and atmospheric transport as well as their combined effects on a quasi-linear OLR-TSrelationship using a conceptual model similar to the C06 model.This model includes turbulent surface fluxes,poleward energy transport,the greenhouse effect of water vapor,and radiative coupling between the atmosphere and surface that follows the Stefan-Boltzmann law.The remainder of the paper is organized as follows.Section 2 describes the radiative-convective-transportive (RCT) energy balance model for a gray atmosphere and methods for evaluating the slope of the quasi-linear OLR-TSrelationship and the degree of the quasi-linearity of the model’s solution.Section 3 presents the results of the RCT model with/without water vapor radiative feedback,with/without surface sensible heat fluxes,and with/without atmospheric poleward energy transport.Finally,the summary of our findings is given in section 4.

2.Model details

We expand the 4-box model of C06 to an energy balance model consisting of 36 equal-area atmosphere-surface columns covering the equator to the pole.As in C06,each atmosphere-surface column consists of two boxes,one for the atmosphere and the other for the surface.The atmosphere is coupled with the underlying surface via the emission/absorption of longwave radiation and exchange of sensible heat.The former by treating the atmosphere as a gray body emitter and the surface as a blackbody emitter;the latter by mimicking vertical convection,which removes energy from the surface and adds it to the atmosphere.Cai and Lu (2007)expanded the physics of the C06’s 4-box model by including temperature-dependent emissivity,hydrological cycle,and temperature-dependent surface albedo to illustrate and isolate the roles of the water vapor feedback,ice-albedo feedback,and poleward moisture energy transport in contributing the polar warming amplification.Following Cai and Lu (2007),we consider a temperature-dependent emissivity to mimic the enhanced greenhouse effect from the water vapor feedback.The energy input to each atmosphere-surface column is determined from the latitudinal profile of the annual mean solar energy flux at the TOA.The gray atmosphere does not absorb any solar energy and the surface reflects part of the incoming solar energy with a prescribed surface albedo(meaning no albedo feedback in this model).These 36 surface boxes do not exchange energy with each other,which effectively treats the surface boxes as land.The 36 atmosphere boxes exchange sensible heat from warm to cold places via a diffusive process that mimics poleward energy transport by atmospheric circulations.Because this model includes vertical radiative energy transfer,vertical sensible heat exchanges between atmosphere and surface,and horizontal energy exchange among the atmosphere boxes,we name this model as radiative-convective-transportive (RCT)energy balance model of a gray atmosphere.This model can be regarded as a symmetric global model about the equator.In that regard,we will plot pole-to-pole latitudinal profiles of the equilibrium solutions of the model covering the entire globe.

Specifically,the RCT energy balance model can be written as

whereσis the Stefan-Boltzmann constant;the subscriptjis the index for the 36 atmosphere-surface columns withj=1 for the column next to the equator andj=36 next to the pole;S jis the annual mean incoming solar energy flux;αjis the prescribed surface albedo (shown in Figs.2a,b are(1-αj)S jand αj,respectively).The remaining symbols in Eq.(1) are unknowns to be determined from the equilibrium solution of Eq.(1).They are (i)TS,jandTA,jfor surface and atmosphere temperatures,(ii) εjtemperature-dependent emissivity,(iii)Fjfor vertical sensible heat exchange between the surface and the atmosphere above,and (iv)Djfor the convergence of poleward energy fluxes represented by a downgradient diffusive process.Note the condition of εj=0 corresponds to the case of no greenhouse gases of any kind in the atmosphere,in which the OLR-TSrelationship would have to be a quartic one per the Stefan-Boltzmann law regardless of the strength of vertical convection and the poleward energy transport.Obviously,the choice of 36 equal-area atmosphere-surface columns is a finite-difference representation of the continuous version of Eq.(1).We have tested that the latitudinal profile of the equilibrium solution for the continuous version of Eq.(1) remains unchanged when increasing the number of equal-area atmosphere-surface columns.

Following Cai and Lu (2007),we consider the following three parameterization schemes that relate εj,Fj,andDjtoTS,jandTA,j:

where,qsis the saturation mixing ratio of water vapor evaluated at the average temperature of an atmosphere-surface column determined by the Clausius-Cl[ape(yron relati)o]n,which is given byin units of kg kg–1withLV=2.5 × 106J kg–1,RV=461 J K–1kg–1,andP=1000 hPa.The four model parameters are ε0(emissivity of dry air),RH (relative humidity expressed as a decimal,which is used to control the strength of water vapor feedback),γ(vertical energy exchange coefficient in units of W m-2K-1),andβ(horizontal energy exchange coefficient in units of W m-2K-1) whose dimensions and values are listed in Table 1.It should be pointed out that the ad-hoc parameterization scheme for the temperature-dependent emissivity is used merely for mimicking the temperature dependency of the water vapor feedback in the gray atmosphere model.The factor (1 -ε0) in the second term on the right-hand side of the first equation of Eq.(2) ensures that the total emissivity varies from ε0(without water vapor feedback) to 1 (with the maximum possible water vapor feedback at which the gray atmosphere becomes the blackbody atmosphere).We have found that the same conclusions can be made by considering different forms of ad-hoc parameterizations for temperature-dependent emissivity.Examples of these different forms include (i)using different values instead of 20 in the first equation of Eq.(6),(ii) replacingin the first equation of Eq.(6) withqS(TA,j),and (iii) usingto replace the first formula in Eq.(2).

The sum of the two equations in Eq.(1) corresponds to the energy balance equation at the TOA

where

Using a standard MATLAB numerical equation solver(FSOLVE),we have obtained the 2×11×11 (242) equilibrium solutions of Eqs.(1) and (2) with the fixed value for model parametersε0,andγ=0,γ=2 W m-2K-1,and 11 varying values for each of RH andβas specified in Table 1.The equilibrium solutions obtained with RH=0 correspond to the case without water vapor feedback and those obtained withβ=0 correspond to the case without poleward energy transport(in this case,the RCT model becomes 36 independent radiative-convective single-column models).The special case ofγ=β=0 corresponds to the case of the absence of vertical convection and poleward energy transport,under which the RCT model becomes 36 independent radiative-equilibrium single-column gray atmosphere models.One can analytically obtain the equilibrium solution of a radiative-equilibrium single-column gray atmosphere model,which is

Therefore,the OLR-TSrelationship in a radiative-equilibrium single-column gray atmosphere model when RH=0 is a quartic one per the Stefan-Boltzmann law.As to be shown shortly,the OLR-TSrelationship in a radiative-equilibrium single-column gray atmosphere model with RH ≠ 0 can be a quasi-linear one because of the greenhouse effect of water vapor.

We use the following two metrics,SLOPE and NRMS,defined below for evaluating the slope of the OLR-TSrelationship and the degree of linearity:

3.Results

3.1.Characteristics of the equilibrium solutions

Shown in Fig.3 are the equilibrium solutions obtained withβ=800 W m-2K-1and varying values of RH for no vertical convection cases.It is seen that the stronger the greenhouse effect is (i.e.,the larger the RH value is),the warmer the surface temperature is.The greenhouse effect of water vapor is stronger in low latitudes than in high latitudes,as evident from the rapid equatorward-increasing profile of the effective emissivity of the gray atmosphere model (Fig.3a).As a result,the stronger the greenhouse effect,the stronger the poleward-decreasing gradient of surface temperature,which results in a stronger poleward energy transport(Fig.3d).The results for cases that include the vertical convection (Fig.4) are otherwise identical to their counterparts shown in Fig.3,with the exception that the presence of vertical convection leads to colder surface temperatures with a weaker poleward-decreasing gradient.

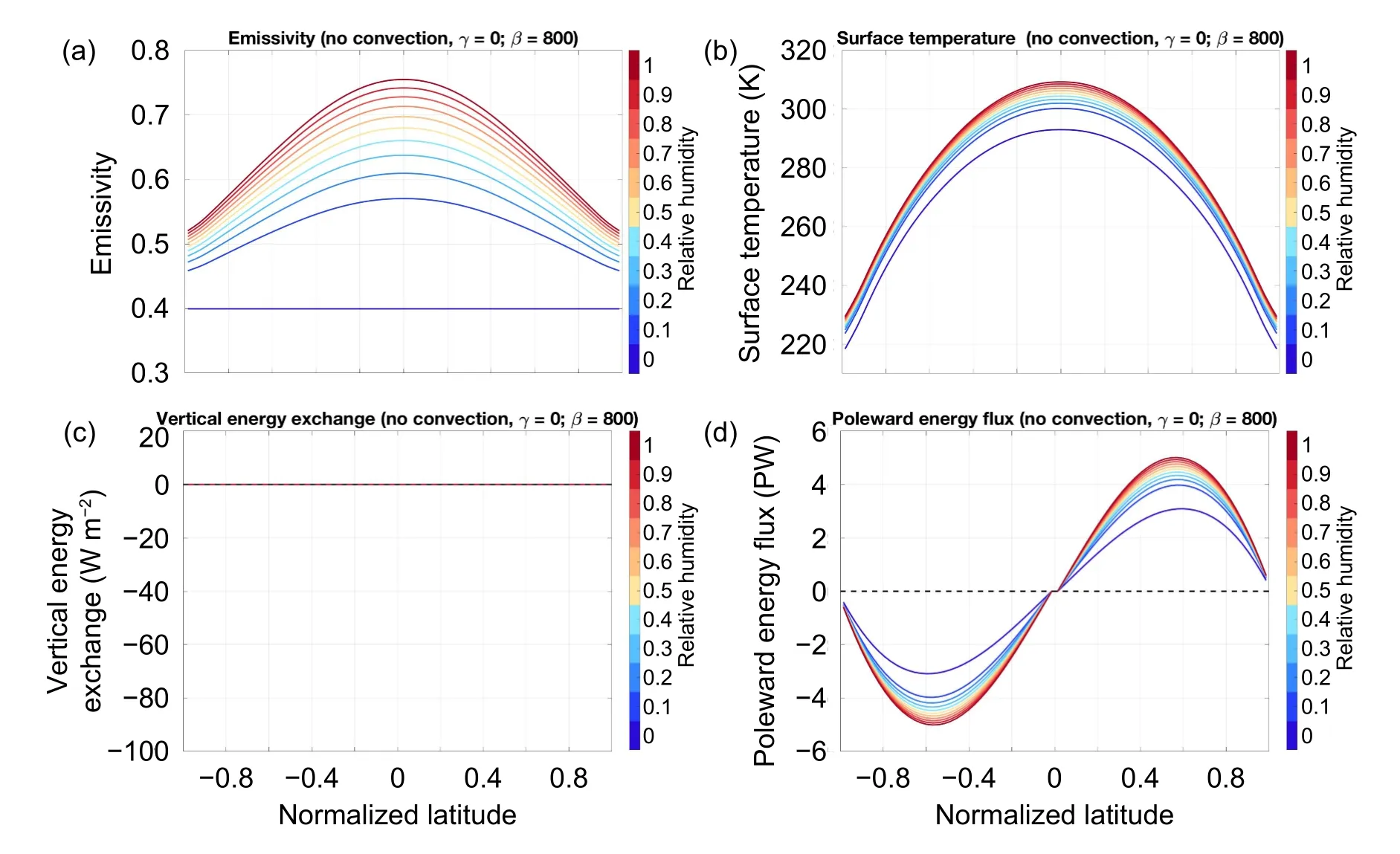
Fig.3.Latitudinal profiles of the equilibrium solutions obtained with γ=0 (no convection) and β=800 W m-2 K-1(fixed poleward energy transport efficiency) using varying RH values (for different strengths of water vapor feedback) indicated by the colors listed to the right of each subplot.The (a) emissivity,(b) surface temperature (K),(c) energy exchange (W m-2) between the surface and atmosphere with negative values indicating loss (gain) of energy at the surface (in the atmosphere),(d) poleward energy flux (PW) determined from horizontal energy exchange among atmospheric layers at different latitudes with positive (negative) values for northward (southward)energy fluxes.

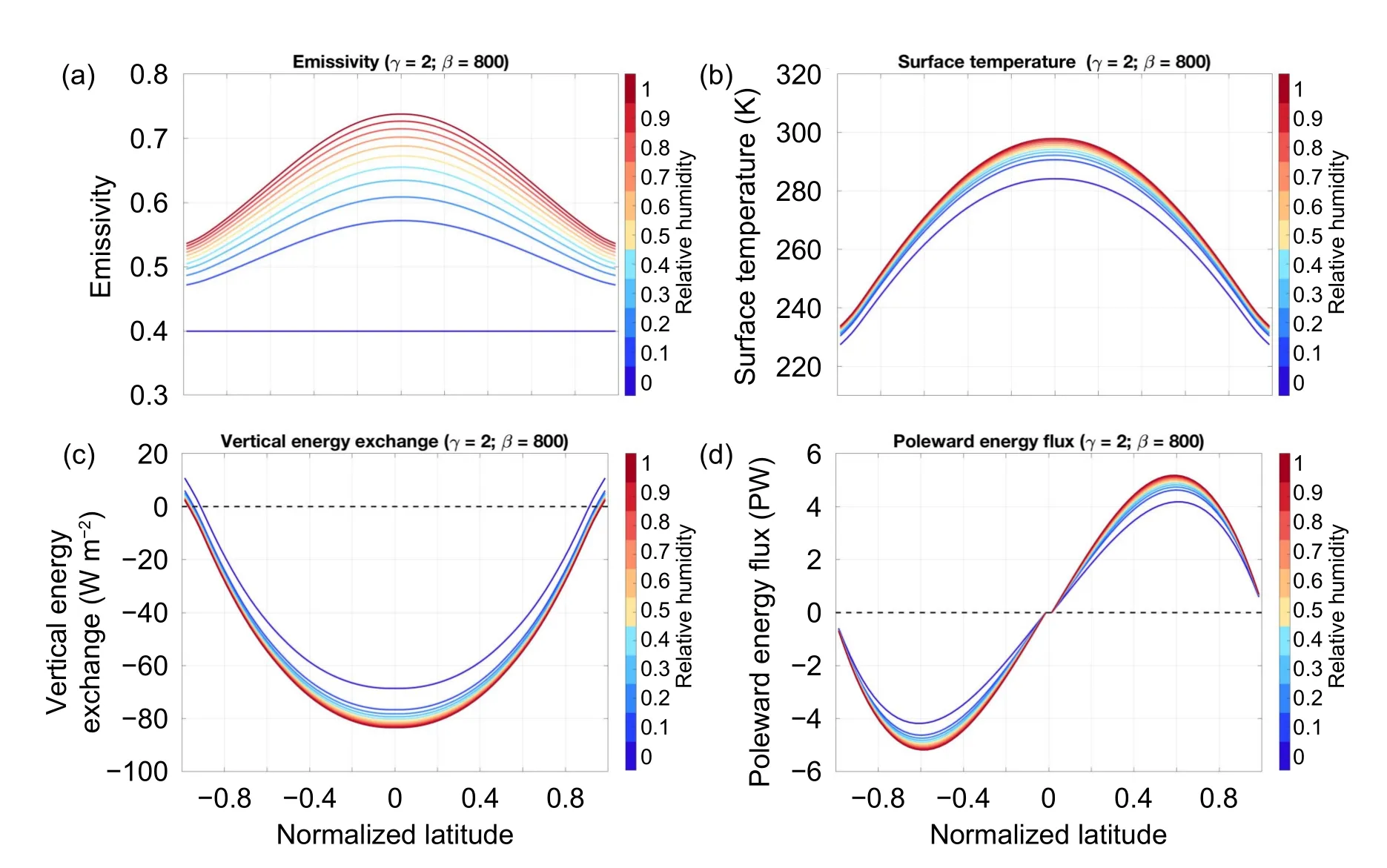
Fig.4.The same as Fig.3 except for solutions obtained with γ=2 W m-2 K-1 (presence of convection).

As expected,the atmospheric poleward energy transport reduces the poleward-decreasing meridional gradient of the surface temperature (Fig.5).It follows that the stronger the poleward energy transport,the stronger the reduction of the poleward-decreasing meridional gradient.The reduction of the poleward-decreasing meridional gradient is achieved by cooling (warming) the tropics (high-latitudes),causing a weaker (stronger) water vapor feedback and thereby a weaker (stronger) greenhouse effect in the tropics (high latitudes) under the same respective RH values (Fig.5a).Such a meridional gradient reduction in the greenhouse effect of water vapor also contributes to a meridional gradient reduction of surface temperature.The reduction of the polewarddecreasing meridional gradient by the atmospheric poleward energy transport is stronger in the atmosphere than at the surface,enhancing (weakening) the vertical convective energy transport in the tropics (high latitudes),as evident in Fig.5c.Therefore,vertical convection also indirectly contributes to the reduction of the poleward-decreasing meridional gradient of surface temperatures.

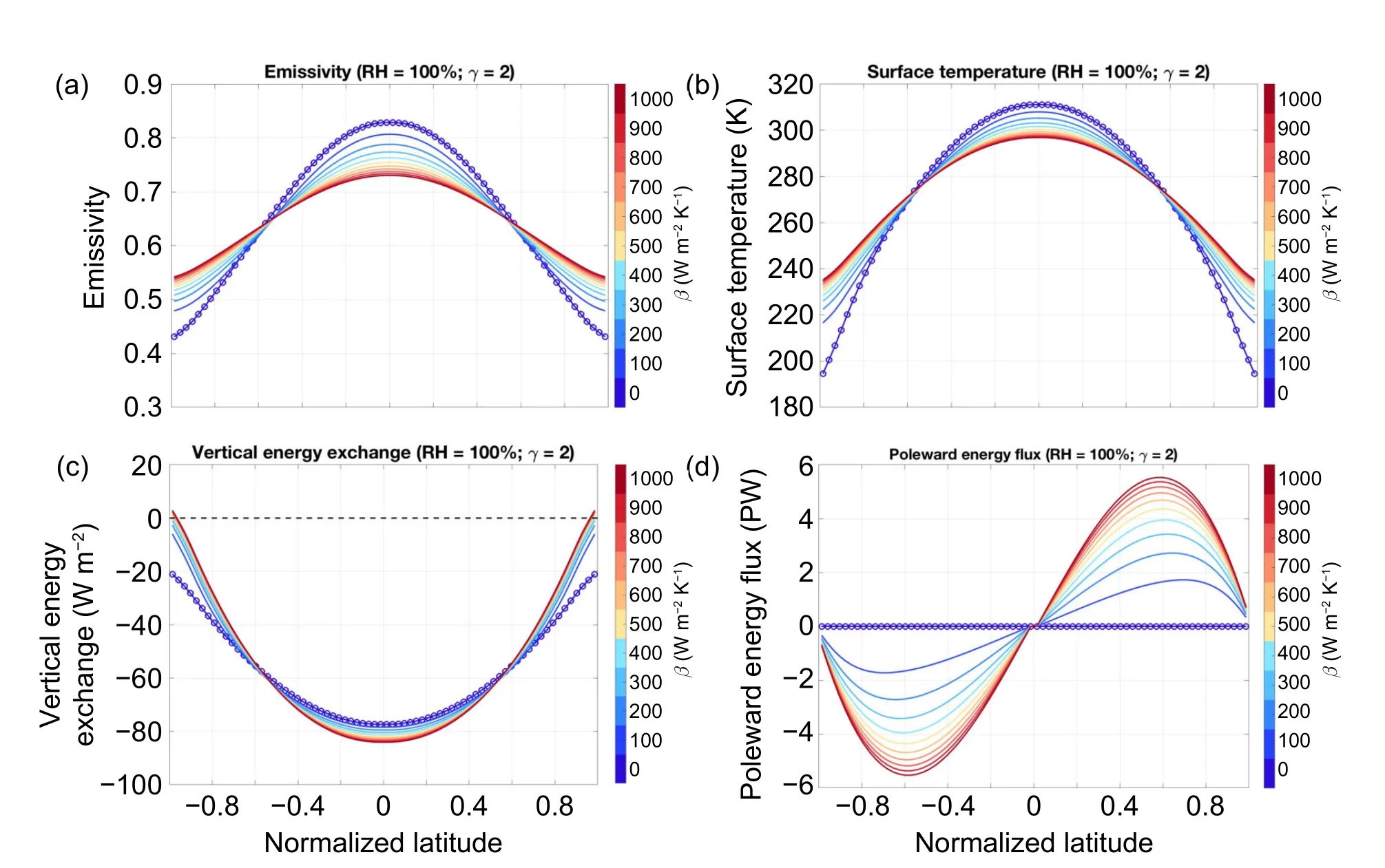
Fig.5.The same as Fig.3 except for the solutions obtained with RH=100%,γ=2 W m-2 K-1 (presence of convection),and varying β values (different strength of poleward energy transport) indicated by colors on the color bar in units of W m-2 K-1.The dotted curves correspond to the case of β=0.

3.2.OLR-TS relation

Figure 6 shows the OLR-TSrelationship for the results in Figs.3–5.It can be seen that the increasing rate of OLR withTSis substantially reduced from the quartic relation in the presence of the greenhouse effect of water vapor and poleward energy transport.The stronger the water vapor feedback,the gentler the slope of the quasi-linear OLR-TSrelationship.Similarly,the stronger the poleward energy transport,the gentler the slope of the quasi-linear OLR-TSrelationship.However,the inclusion of vertical convective energy transport increases the slope of the quasi-linear OLR-TSrelationship while reducing the degree of quasi-linearity.

Figure 7 summarizes the slope of the quasi-linear OLRTSrelationship and the degree of their quasi-linearity obtained from the 242 eqsuilibrium solutions of the RCT energy balance model of a gray atmosphere under the parameter settings listed in Table 1.The conclusions drawn from the selected numerical experiments of the RCT energy balance model,as shown in Fig.6,apply to all of the 242 experiments.The cases of RH=0 (represented by dots with the bluest color in Fig.7) illustrate that poleward energy transport alone without the water vapor feedback can lead to a reduction of the increasing rate of the OLR-TSrelationship with the surface temperature.Both the slope reduction of the OLR-TSrelationship and the degree of the quasi-linearity (measured by smaller values of NRMS) increase as the strength of the poleward energy transport increases.The cases ofβ=0 (represented by dots along the vertical axis with PW=0) illustrate that both the slope reduction of the OLR-TSrelationship and the degree of the quasi-linearity increase as the strength of the water vapor feedback increases in the absence of the poleward energy transport.The combined effect of the water vapor feedback and poleward energy transport is that the quasi-linear OLR-TSrelationship is gentler with a higher degree of quasi-linearity as the strength of the greenhouse effect and enhanced poleward energy transport is increased.When the vertical convective energy transport is suppressed,the increasing rates of the quasi-linear OLR-TSrelationship with the surface temperature under the same strength of the greenhouse effect of water vapor and poleward energy transport are slower,and the degree of their quasi-linearity is higher.Therefore,the so-called quasi-linear OLR-TSrelationship by itself is just a mathematical relationship that reflects the collective or combined effect of radiative and non-radiative processes that determine the latitudinal pattern of surface temperature.

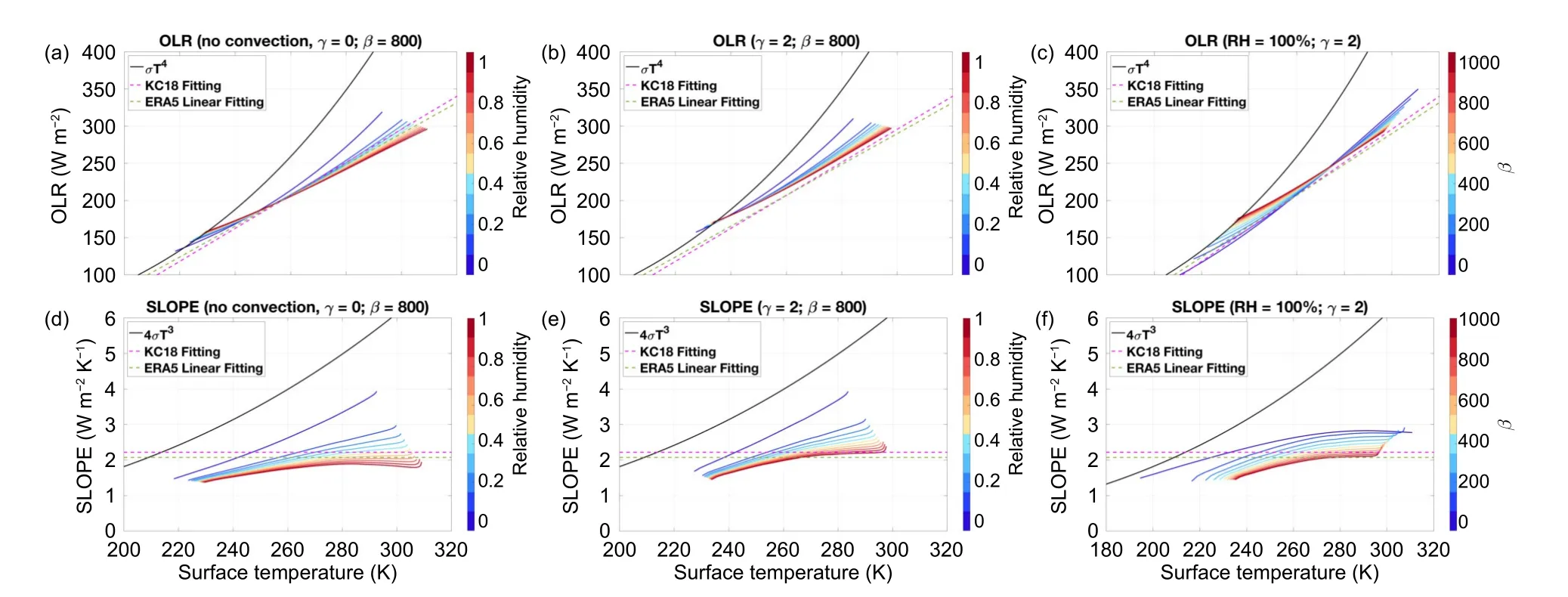
Fig.6.Variations of OLR (W m-2,ordinate in the top row) and its derivative with respect to the surface temperature (W m-2 K-1,ordinate in the bottom row) as a function of surface temperature (K,abscissa).The left column is for the experiments without convection (γ=0),but with the poleward energy transport (β=800 W m-2 K-1) and varying RH whose values are indicated by the color bar;the middle column is for the experiments with convection (γ=2 W m-2 K-1),poleward energy transport (β=800 W m-2 K-1) and varying RH values whose values are indicated by the color bar;and the right column is for the experiments with convection (γ=2 W m-2 K-1) and a fixed 100% RH but a variable β,whose values are indicated by the color bar.The black curves correspond to the OLR (top row) and its first derivative with respect to surface temperature (bottom row) per the Stefan-Boltzmann law.

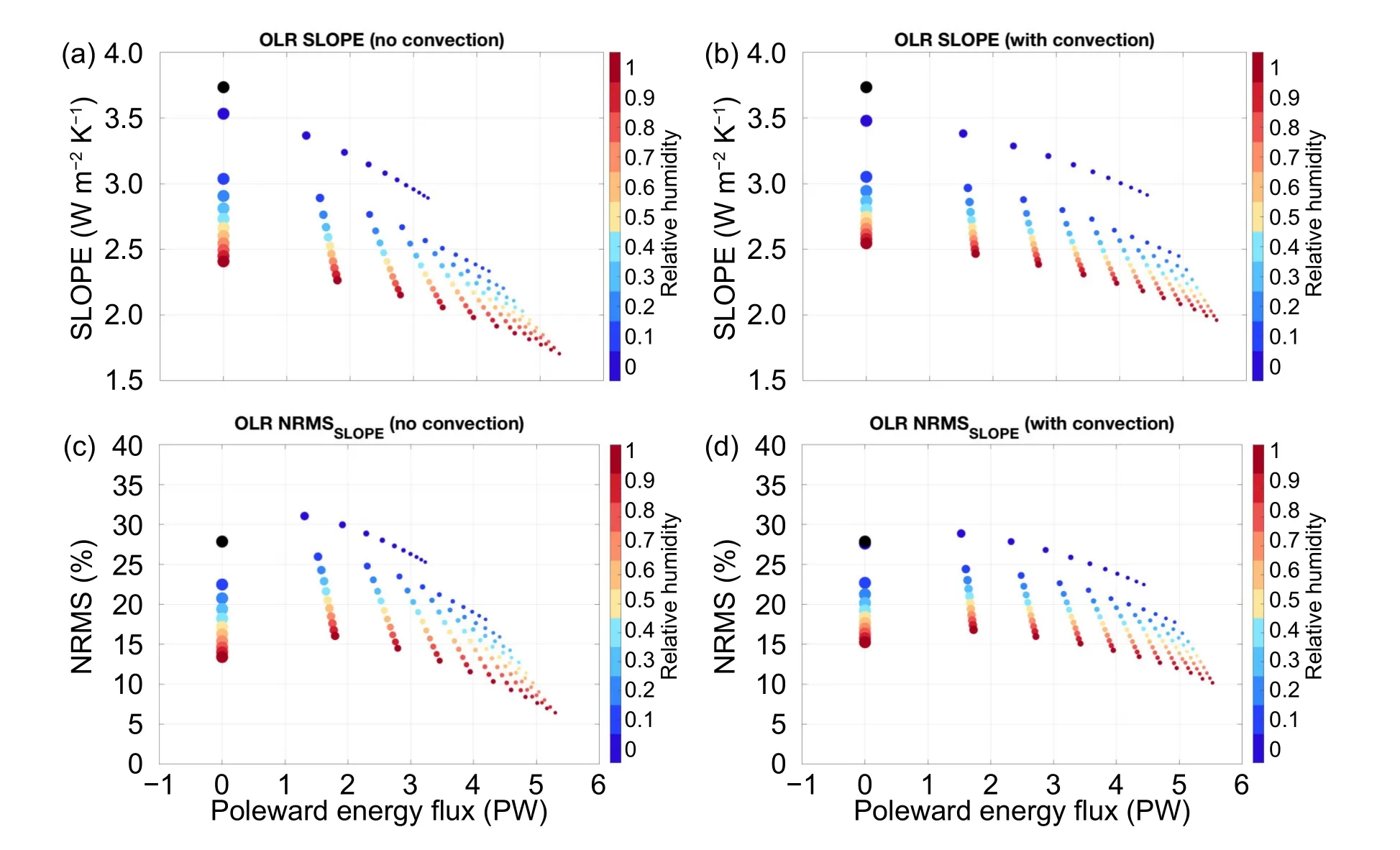
Fig.7.Scatterplots of SLOPE (ordinate of the top row,in units of W m-2 K-1) and NRMS (ordinate of the bottom row,in units of %) for the OLR-TS relationship of the 11 × 11 equilibrium solutions obtained with γ=0 (left column for no convection) and γ=2 W m-2 K-1 (right column for the presence of convection) against their peak values of poleward energy fluxes (abscissa,in units of PW).The color bar indicates RH values.The solid black dots are for the OLR-TS relationship per the Stefan-Boltzmann law.The size of the colored dots is representative of the strength of the poleward energy transport per unit of meridional temperature contrast with the largest size for β=0 (no poleward energy transport) and the smallest for β=1000 W m-2 K-1.

To further substantiate the conclusion that the quasi-linear OLR-TSrelationship by itself is not solely determined from the longwave radiative transfer process alone,we have made the same mathematical analysis using Eqs.(6) and (7)but for the net downward solar energy flux at the TOA(Fig.8).Because the net downward solar energy flux at the TOA is the same for all of the 242 experiments,the differences in SLOPE and NRMS shown in Fig.8 are all caused by the differences inTS.According to Fig.8,the latitudinal variation of surface temperature in the RCT model can be uniquely and approximately determined from the latitudinal variation of the solar energy input according to a mathematical quasilinear relationship.The slope of the quasi-linear relationship and its degree of quasi-linearity (or the accuracy of the quasi-linear approximation) depends on the individual strength and their combination of the parameterized greenhouse effect,vertical convective,and poleward energy transport.Note that the latitudinal profile of the OLR in an equilibrium climate state can be modified directly only by the poleward energy transport but not by the greenhouse effect of water vapor nor by vertical convection (because the OLR in an equilibrium climate state would have to be exactly equal to the net downward solar energy fluxes at the TOA in the absence of poleward energy transport).However,none of these three processes can directly modify the latitudinal profile of the net downward solar energy fluxes at the TOA.Therefore,any change in the increasing rate of surface temperature with the net downward solar energy fluxes at the TOA is made mainly through the change of the meridional temperature gradient with a little change in the net downward solar energy fluxes at the TOA,which is particularly true in the RCT model where there is no cloud and the surface albedo is fixed.The meridional gradient of surface temperature increases as the greenhouse effect of water vapor increases but decreases as the strength of poleward energy transport and/or vertical convective energy transport increases.As a result,the slope of such a quasi-linear approximation using the latitudinal variation of the solar energy input for estimating the equilibrium surface temperature is steeper for stronger poleward energy transport and stronger vertical convective energy transport,but gentler for stronger water vapor feedback.The accuracy of such a mathematical quasilinear approximation is higher in a radiative-convective-transportive energy balance model than in a radiative-convective model.The improved understanding of the individual and combined effects of radiative and non-radiative processes helps to explain why the slope of the quasi-linear approximation varies with the parameterizations of these radiative and non-radiative processes in the RCT energy balance model.

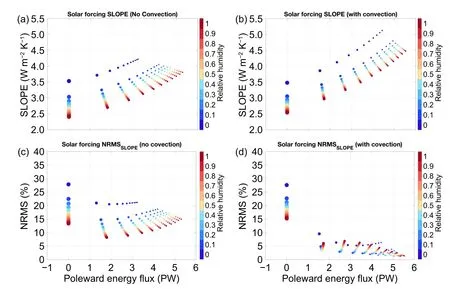
Fig.8.The same as Fig.7 but for the dependency of TS on the net downward solar energy flux at the top of the atmosphere.

One would expect that the quasi-linear relationship of the net downward solar flux at the TOA withTSderived in the simple RCT energy balance model would also exist in observations,because of the energy-balanced nature of the observed climate state.To substantiate this conjecture,Fig.9 plots the Gaussian kernel density function of the annual mean net downward solar energy fluxes at the TOAagainst the surface temperature using the ERA5 reanalysis data.It can be seen that the high-density region of data points in thedomain (as indicated by the yellowish colors in Fig.9) generally lies along a positively sloped straight line,confirming a quasi-linear relationship between the annual mean net downward solar energy fluxes at the TOA and surface temperature in observations.The quasi-linear relationship is also evident from the large R-squared values of the linear regression analysis for data points in thedomain in both hemispheres.The slope of such a quasi-linear relationship is much steeper than that of its counterpart for the OLR-TSrelationship(Fig.9 versus Fig.1),consistent with the results obtained from the simple RCT energy balance model (Fig.8 versus Fig.7).Note that the quasi-linear,relationship breaks down over the Antarctic region where the surface temperature varies greatly due to the spatial variation of the surface elevation under the same value of(about 50 W m-2).

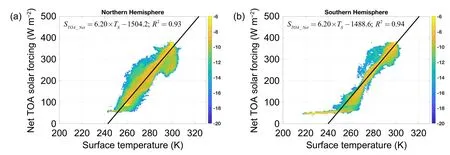
Fig.9.The Gaussian kernel density function (shadings,in logarithmic scale) for the observed relationship between the annual-mean net downward solar energy flux at the TOA (ordinate in units of W m-2) and surface temperature (TS,abscissa in units of K) for the (a) Northern Hemisphere and (b) Southern Hemisphere.The total number of data points in each panel is 1 389 330,corresponding to the 1° × 1° spatial resolution covering each hemisphere for the 43 years spanning 1979–2021.The black solid lines are linear regression lines whose mathematical expressions and R-squared values are given in the topleft corner of each panel.To avoid the complication due to the high elevation over the Antarctic,the regression analysis for the Southern Hemisphere is made without considering data points within 65°–90°S.

4.Summary

In this study,we advance a so-called radiative-convective-transportive energy balance model of a gray atmosphere to examine the individual effects of water vapor feedback,vertical convection,and atmospheric transport as well as their combined effects for a quasi-linear OLR-TSrelationship.The use of a gray atmosphere for showing the existence of a quasi-linear OLR-TSrelationship provides a counter-example for KC18’s explanation about the observed quasi-linear OLR-TS,which postulates that the quasi-linearity is a result of more abundant water vapor at higher temperatures that narrows down the atmospheric window through which the surface thermal emission can escape to space.Our interpretation of the quasi-linear OLR-TSrelationship is different from that provided in KC18,aside from the consideration of the effect of the poleward energy transport.Specifically,the KC18’s quasi-linear OLR-TSrelationship is obtained directly from the output of a line-by-line radiation transfer model using the surface temperature as part of the input field without considering the energy balance.Unlike KC18,the quasi-linear OLR-TSrelationship is obtained in this study by explicitly considering the energy balance such that both surface and air temperatures,as well as the OLR and water vapor,are the solutions of an equilibrium climate state.In particular,the quasi-linear OLR-TSrelationship in the absence of poleward energy transport is achieved through the greenhouse effect of the water vapor feedback that serves to increase the meridional gradient of the surface temperature without altering the OLR.The condition that the OLR cannot be modified by the greenhouse effect alone in an equilibrium climate state serves as direct evidence indicating that the atmospheric window effect does not apply to the quasi-linear OLR-TSrelationship found in the gray atmosphere model.

The main motivation of this study is to provide a more general explanation for the observed quasi-linear OLR-TSrelationship that does not require the existence of the atmospheric window for planetary thermal emission.Because the slope of the quasi-linear OLR-TSrelationship is regarded as the most important parameter measuring the climate sensitivity parameter (e.g.,Bony et al.,2006),a better understanding of the processes that determine the slope of the quasi-linear OLR-TSrelationship would help advance our prediction capability for how the Earth climate system would respond to anthropogenic radiative forcing.The main findings are summarized below.

(1) The meridional gradient of surface temperature increases with the strength of the greenhouse effect of water vapor,contributing to a substantial reduction in the increasing rate of the OLR with surface temperature so that the OLRTSrelationship becomes a linear one,instead of the quartic relation as per the Stefan-Boltzmann Law.In the absence of the poleward energy transport,the increase in the meridional gradient of surface temperature by the water vapor feedback alone can lead to a quasi-linear OLR-TSrelationship without altering the OLR.

(2) The effect of the atmospheric poleward energy transports flattens the latitudinal profiles of both OLR and surface temperature,which also contribute substantially to the quasilinear increasing rate of OLR with surface temperature.

(3) The effect of vertical convective energy transport directly reduces the meridional gradient of surface temperature without directly affecting the meridional gradient of the OLR.It thereby acts to weaken the reduction of the increasing rate of OLR with surface temperature caused by the water vapor feedback and poleward energy transport.

(4) The quasi-linear OLR-TSrelationship by itself does not necessarily reflect the degree of the opacity of the atmosphere for upward longwave thermal radiation.Instead,it reflects the individual and combined effects of their radiative(e.g.,the greenhouse effect) and non-radiative (e.g.,poleward energy transport) components on the meridional gradients of both surface temperature and OLR.Therefore,the quasilinear OLR-TSrelationship should be regarded as a mathematical approximation of the latitudinal variation of OLR using the latitudinal variation of surface temperature or vice versa.The understanding of the individual and combined effects of radiative and non-radiative processes helps to explain why the slope of the quasi-linear approximation varies with the strength of these radiative and non-radiative processes.

(5) Because of the nature of the energy-balanced climate system,such a quasi-linear approximation is equally applicable to the relationship between the net downward solar flux at the TOA withTS,albeit with a steeper slope.

(6) Our physical understanding of the individual and combined effects of radiative and non-radiative processes on the slope of the OLR-TSrelationship can also help explain how these processes individually and collectively affect the slope of the mathematical relationship of the net downward solar flux at the TOA with surface temperature.A stronger water vapor greenhouse effect,which acts to enhance the meridional gradient of surface temperature,favors a gentler slope.Stronger vertical convection favors a steeper slope,as it acts to reduce the meridional gradient of surface temperature,which is also the same as its effect on the OLR-TSrelationship.However,the poleward energy transport affects the mathematical relationship of the net downward solar flux at the TOA with surface temperature in an opposite way from its effect on the OLR-TSrelationship.Specifically,the same reduction of the meridional gradient of surface temperature by poleward energy transport would favor a steeper slope instead of a gentler slope as the case for the OLR-TSrelationship.

Acknowledgements.This research was in part supported by grants from the National Natural Science Foundation of China(Grant Nos.42222502 and 42075028) and grants from the National Science Foundation (AGS-2032542 and AGS-2202875).The authors are grateful for the constructive comments and suggestions from the editor and two anonymous reviewers.

Data availability statement.The ERA5 reanalysis is downloaded at https://doi.org/10.5065/P8GT-0R61.Upon reasonable request,all model codes and data analysis codes will be made available to researchers interested to reproduce the results.The authors declare no competing interests.