面向循环寿命最优的电池组串-并混联结构设计方法研究

裴 磊，吴宝坤，王天鸶，盘朝奉

(1.江苏大学汽车工程研究院，江苏镇江 212013；2.江苏大学汽车与交通工程学院，江苏镇江 212016)

随着电动汽车与储能系统所需的储能需求日益增长，其配套锂离子电池组的拓扑尺寸也在不断增长。然而，由于制造过程中电池间关键性参数的不一致，使得成组电池并不能简单等效为单体电池性能的克隆与叠加，成组的形式、结构与匹配，都会严重影响成组后的整体性能，包括但不限于电池组的可用容量和循环寿命。

这些限制电池成组性能的问题主要来源于组内单体电池的不一致性。在工业应用领域中，电池出厂时的工作电压、内阻以及可用容量等方面的差异会导致成组电池存在不一致性。同时，随着不断充放电循环使用，电池组各单体间的不一致程度将进一步增大，电池组的性能衰减速率也将远远大于电池单体的行为，最终制约电池组的整体性能[1]。目前，电池连接方式主要有串联与并联，其在安全、性能与成本方面各有优劣。串联方式使得各单体老化速率趋于一致，而最弱的单体总是决定整个电池组的性能且硬件成本较高；并联方式则具有一定的自平衡能力和对电池开路故障的容错能力，但并联内部电流的不一致现象会加速电池组的“短板效应”。而这两种连接方式各自的劣势可以被相互弥补，当串联电池组中某一单体出现故障时，其电池组电压平台将降低，结合并联方式则可以维持其工作电压；并联电池组中的不平衡电流现象也可以通过添加串联方式进行抑制。因此，寻找出减缓电池组循环寿命衰减的串联与并联配置方式，可以最大程度发挥电池组的整体性能，实现储能系统的效益最大化。

为了最大限度发挥成组电池的整体性能，需要求出指定容量、电压条件下的最佳串并联结构，使得电池组的循环寿命最优。为此，需要从电池组建模和寻优策略两方面进行研究。

在电池组建模方面：文献[2]以单体等效电路模型为基础，建立了电池组放电特性的数学模型，并通过不同的串并联成组实验验证了该模型评估放电容量的有效性，但其忽略了工业场景中实际参数间存在的不一致性影响。在明确电池初始制造过程所存在的参数不一致性问题，文献[3]以电化学热模型为基础，同时加入对阴极固体体积分数与温度的参数变化的考虑，建立起计及老化的锂离子电池组电化学模型。该模型能够表征恒定工况下的电池组容量损失轨迹，然而随着电池组的老化，相同电流倍率在其不同老化阶段将产生差异性的影响，这使仅面向恒定工况的电池模型难以预测电池组全生命周期的容量损失轨迹[4]。

在寻优策略方面：文献[5]采用基于数理统计模拟参数的大规模电池成组仿真方法，并结合并联支路不均衡电流仿真，通过不断地对不同串并联结构的电池组建模仿真分析，遴选出最佳的电池组串并联结构，结果显示，电池组先并后串是最佳的连接拓扑，因为该结构将电池组的可用容量最大化并降低了参数的分散性。文献[6]使用蒙特卡罗模拟来量化随机采样下四种典型连接拓扑下参数变化对电池组可用容量和功率的影响，得到了不同拓扑结构电池组的容量均值和方差表达式，结果表明，电池先并后串连接的电池组可以更好地降低电池参数变化的影响，获得更高的性能，大大提高可用容量和能量利用率。文献[7]提出了表征电池组容量分散性的容量极差和容量分散度指标，基于电池Thevenin 等效电路模型构建电池组模型并仿真得出了最大化电池组可用容量的组合方式。上述仿真分析遴选的方法在面临大型阵列设计过程中存在的众多拓扑问题时，逐一建模工作量巨大且可扩展性差。

为了兼顾电池组循环寿命预测的准确性与最佳结构寻优的高效性，本文提出一种面向循环寿命最优的锂离子电池串并联结构优化设计方法，其具体流程如图1 所示。首先，在经典Thevenin 模型上添加对活性锂损失与对随容量损失变化的特征参数的计算，进而结合对组内不一致参数的表征，完成对电池组老化行为的刻画。其次，从囊括商用成组方式的典型结构出发，基于所述电池组建模方法构建典型结构模型并仿真以形成预测样本集；在此基础上，利用预测样本集并结合非线性推衍预测方法，得出所有结构的循环寿命，最终完成对最佳拓扑结构的标定。

图1 整体算法流程图

1 电池组老化行为建模方法

为了准确预测电池组的循环寿命，本节分别从单体电池的老化行为表征与电池组参数不一致性影响分析两个方面开展了针对性的研究工作，具体流程对应图1 中的“面向循环寿命最优的电池成组串并联结构设计方法”下的“单体Thevenin 老化行为模型”与“电池组老化行为模型”环节。

1.1 单体电池老化行为模型

不同于新电池建模仅需要考虑其在短时间尺度下的动态行为，对于老化电池的建模则需要在典型动态行为建模的基础上，考虑到模型中各个参数在电池长时间尺度运行过程中的性能衰退与数值演变，故对非全新电池行为的建模需要同时兼顾其“动态”与“老化”两个方面。

1.1.1 短时间尺度下的单体电池动态行为

在短时间尺度下，刻画出单体电池瞬时的电压行为是模型的基础。在考虑电池的电特性与系统实际的采样能力下，选择Thevenin 等效电路模型作为建模基准，其具体模型形式与数学表达式分别如图2与式(1)所示。图中：Ubat为电池端电压，V；Ibat为流经电池的总电流，A；OCV为电池的开路电压；Ro、Rp分别为电池的欧姆与极化内阻值，Ω；Cp为极化电容；ηo、ηp分别为欧姆过电势与极化过电势，V；Ip为电池的扩散电流，A。

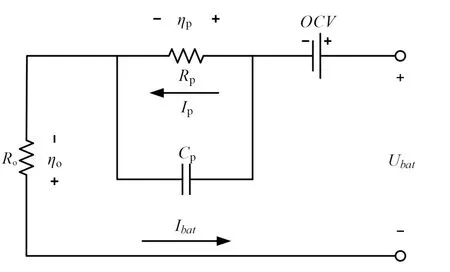
图2 Thevenin模型

进一步地，本文将阐述电池容量损失的连续递推计算方法，以及构建容量损失与单体模型各参数的关系，进而将经典模型的适用范围从短时间尺度拓展至长时间尺度。

1.1.2 长时间尺度下的单体电池老化行为

在长时间尺度下(即随着电池不断老化)，与电池健康状态高度相关的特征量如开路电压、欧姆内阻则会发生变化。因此，捕捉电池的容量损失与其特征量变化的动态行为则是建模的重点。在容量损失行为方面，在电池的循环老化过程中，SEI 的生成与增长过程中锂离子的消耗是导致容量损失的主要原因[8]。为此本节基于文献[9]中所建立的容量损失递推计算的集总参数模型，得到活性锂损失(LLI)与等效充电时间的关系，如式(2)所示。

式中：θ1～θ3为待实验确定的系数；Tk、Tstd分别为第k时刻的温度与标准温度(Tstd=303 K)；Δtchg,k为两次监测期间的充电时间，h；Closs,k为第k时刻的电池容量损失，Ah。

在特征量随容量损失变化的行为方面，在电池容量衰减的同时，电池的OCV曲线也会发生对应的影响。基于文献[10]在电极电势联合坐标系下的变化规律分析可知：随着电池的老化，电池的OCV曲线与其荷电状态(SOC)的整体对应关系并不会发生变化，而是仅仅体现为在高SOC电压平台的逐渐消失。为此，通过进行不同老化状态的电池OCV曲线标定实验[如图3(a)所示]，可以插值得到不同健康状态(SOH)条件下电池的开路电压三维曲面，如图3(b)所示。图3(a)中OCV曲线标定实验具体流程如下：在单体电池标准循环老化实验(1C/25 ℃)过程中，于其初始状态及每200 次循环后，对其进行一次放电倍率为1/20C的满放电实验，进而得到其在不同SOH下的OCV-SOC曲线。

图3 OCV曲面获取

电池容量损失在影响电池OCV参数的同时，同样会对电池的内阻情况产生对应的影响。基于文献[11]中对于LLI 损失与电池欧姆内阻增量之间作用关系的理论分析，得到其内阻增量与其电池容量损失之间的函数关系，如式(3)所示。

式中：α1、α2为需要通过实验确定的模型参数。

此外，对于单体模型中的RC 环节，由于其数值主要取决于电池材料自身的扩散速率与粒子半径，而二者又主要受到活性材料损失的影响，所以在电池的常规老化阶段，其随电池容量损失的变化量值可以忽略不计[4]。

1.1.3 电池行为模型老化参数获取

为获取单体模型在长时间尺度下的老化相关参数与分布情况，4 节电池被串联以同步进行标准循环老化实验(1C/25 ℃)，且每隔指定循环数，分别标定各单体容量等参数，具体实验流程如图4 所示。

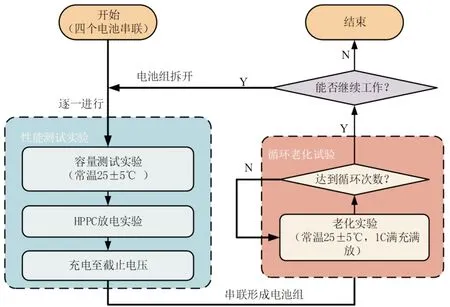
图4 单体电池老化参数标定实验

基于所得各电池容量及内阻变化情况，分别对式(2)与式(3)进行最小二乘参数拟合，进而获取电池老化参数的分布情况，容量损失与内阻增长的拟合效果如图5 所示。

图5 容量损失与内阻增长的拟合效果

1.2 电池组老化行为模型

在电池组建模仿真前，各电池特性参数需率先设定于电池组模型中。目前，通过对各单体电池进行性能测试实验与参数辨识是标定电池组模型的常规手段，而需要大规模电池组建模仿真时，实验方法失效。根据现有研究结果发现：同批次电池的内阻与容量等初始参数相互独立且均遵循高斯分布[12-14]。因此，通过统计部分电池参数以获取符合正态分布的电池初始参数分布，解决了大规模电池组初始参数获取困难这一难题。故此，本文以储能及商用车领域广泛应用的磷酸铁锂/石墨(LFP/GIC)电池为研究对象，对将要进行成组实验的部分电池样本分别进行容量标定与混合脉冲功率特性(HPPC)实验，并利用最小二乘法辨识模型参数，进而获取基础电池模型在短时间尺度下的初始参数分布情况，如表1 所示。

表1 初始参数分布情况

此外，各电池间的内阻、容量、电压等参数不一致将导致个别单体率先达到电压截止条件，故仿真过程中需实时监测各电池电压，以避免率先达到电压截止条件的电池出现过充或过放情况。以磷酸铁锂/石墨电池为实验样本，成组使用时各单体电压vi(V)的充放电压限制如下：

2 基于典型结构的电池组循环寿命推衍预测方法

在给定电池阵列设计条件下，为了寻优最大限度减缓电池组循环寿命的连接结构，现有研究的解决方法为对所有结构进行建模仿真。该方法存在着自动化程度低、超大规模无法穷举、大规模电池组计算量大等问题。为此，本节提出一种推衍预测方法：基于有限多个囊括商用成组形式的典型结构与所述电池组建模方法得到的典型结构循环寿命，通过多元回归与神经网络方法进行预测，最终实现对最佳拓扑的标定，从而解决了大型阵列无法穷举、计算量大等问题，具体流程对应图1 中“面向循环寿命最优的电池成组串并联结结构设计方法”下的“循环寿命推衍预测方法”环节。

2.1 典型结构的选择

在工业应用领域，电池成组方式至多为从模组到电池包，主要包括先串后并结构、先并后串结构以及两者结合的混联结构。此外，在预测过程中，作为预测样本的典型结构应尽可能呈均匀分布，以降低在样本密集处过多训练而在样本较少区域训练痕迹不明显所导致预测能力较差的概率。基于以上原则，本文分别选取电池组总电池数为16、32、64、128的不同串并联结构作为典型结构，具体可分为先串后并与先并后串顺序结构，如表2 所示。

表2 电池组典型仿真结构

2.2 电池组循环寿命推衍组合预测方法

在推衍预测方面，由于拓扑结构到循环寿命为非线性的映射过程，故选取非线性预测领域中较为经典的多元回归与BP 神经网络方法。此外，作为预测方法输入量的连接结构，需被数字化表示以供预测网络识别。这里，连接结构通过包含串并联数目的1×4 向量完成描述。例如，“先4 串后4 并”结构通过[4,4,1,1]矩阵完成描述。其中，为避免预测方法参与识别上述串并联顺序类型而影响预测效果，分别对两类串并联顺序结构进行训练与预测。例如，“先2 并2 串再2 并”结构与“先2 串2 并再2 串”结构均以[2,2,2,1]矩阵描述。

(1)多元回归

多元回归预测是研究多个自变量与一个因变量之间回归关系的预测方法。对于拓扑结构与循环寿命之间的非线性关系而言，我们选择带常数项、线性项与交叉项的多元回归模型，如式(5)所示。

(2)BP 神经网络

BP 神经网络模型作为一个非线性模型，优于处理复杂模糊的映射关系且不需知数据的分布形式和变量间的关系[15]，可用于拓扑结构性能的推衍预测。因训练样本不多，单次回归预测误差较大，为减小回归预测的误差，取100 次预测结果的中位数作为最终的预测结果。

此外，由于单项预测方法往往仅包含预测样本集的部分信息，通过一定规则组合各单项方法以包含更全面的预测信息，从而降低预测出现更大偏差的概率[16]。组合预测方法的计算公式如下：

这里采用的算法均为经典的多元回归与BP 神经网络算法，相关算法在MATLAB 中实现。不同的是，训练样本集由本节所提典型拓扑结构及其电池组模型的仿真结果构成。

3 实验与结果分析

为了验证本文所提电池组建模方法和循环寿命推演预测方法的有效性，本节以储能及商用车领域广泛应用的磷酸铁锂/石墨电池为实验对象，以可囊括所有拓扑结构类型的最小阵列为设计对象(即串并联数均为4 的4×4 电池阵列)，通过串-并混联结构设计方法，获取最优结构并结合成组老化实验，验证所获最优结构的有效性。

3.1 推衍预测效果验证

在推衍预测环节，考虑到所有结构的循环寿命是由典型结构的仿真结果推衍预测所得，故推衍预测方法的精度验证，均选择对应拓扑结构下的模型仿真值作为参考值。这里，在给定4×4 电池设计阵列下，分别得到电池组老化行为的模型仿真值、基于典型结构的推衍预测值及其间误差如表3 所示。需要说明的是，为了与3.3 节中实物实验的循环次数保持统一，仿真与推衍结果均选择1 000 次循环作为预测终点，即表中的SOH值均为1 000 次循环后的预测值或仿真值。可以看出，预测误差被控制在±2%以内。

表3 推衍预测结果与误差 %

3.2 最优结构获取

将所述电池组串-并混联结构设计方法在MATLAB-Appdesigner 中进行封装，形成可视化图形界面软件，如图6(a)所示。利用该软件，通过对目标参数的输入(初始参数分布、老化参数分布、运行工况)，即可自动获取所有结构下的循环寿命值，如图6(b)所示，最优结构即为“先2 并2 串后2 并2 串结构”。

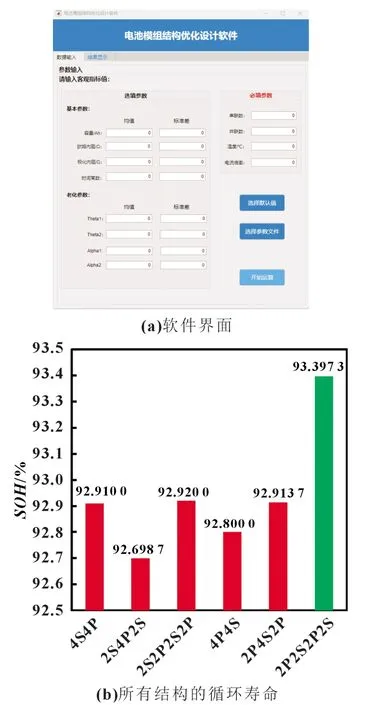
图6 所有结构的循环寿命

3.3 电池组老化行为模型与寻优结果验证

为了验证所述建模方法与寻优结果的准确性，在电池组模型方面，分别选取目前经典的“先4 并后4 串结构”与根据本文所提方法得到的循环性能最佳的“先2 并2 串后2 并2 串混联结构”，作为验证样本，进行标准循环老化实验，如图7 所示。考虑到两种电池组初始参数不一致的差异影响，选取的两种成组结构的电池初始参数分布情况如表4 所示，可以看出，两类结构的成组初始参数分布不一致差异程度较小，故参数不一致差异的影响可以被忽略。

表4 两种结构的电池初始参数分布情况

图7 电池组老化实验

对选取的成组结构在1C/25 ℃、满充满放条件下进行累计1 000 次循环的老化实验，其中充电采用恒流-恒压(CC-CV)，放电采用恒流(CC)方式。同时，对所建电池组模型在相同工况下进行循环充放电仿真，两种结构容量变化的测量、仿真结果与误差如图8 所示。考虑到初始的不一致参数分布，仿真结果取5 次仿真后的中位数。为了直观反映电池在整个寿命周期中的容量衰减趋势，电池的容量情况将以电池的SOH形式进行表述，如式(7)所示。

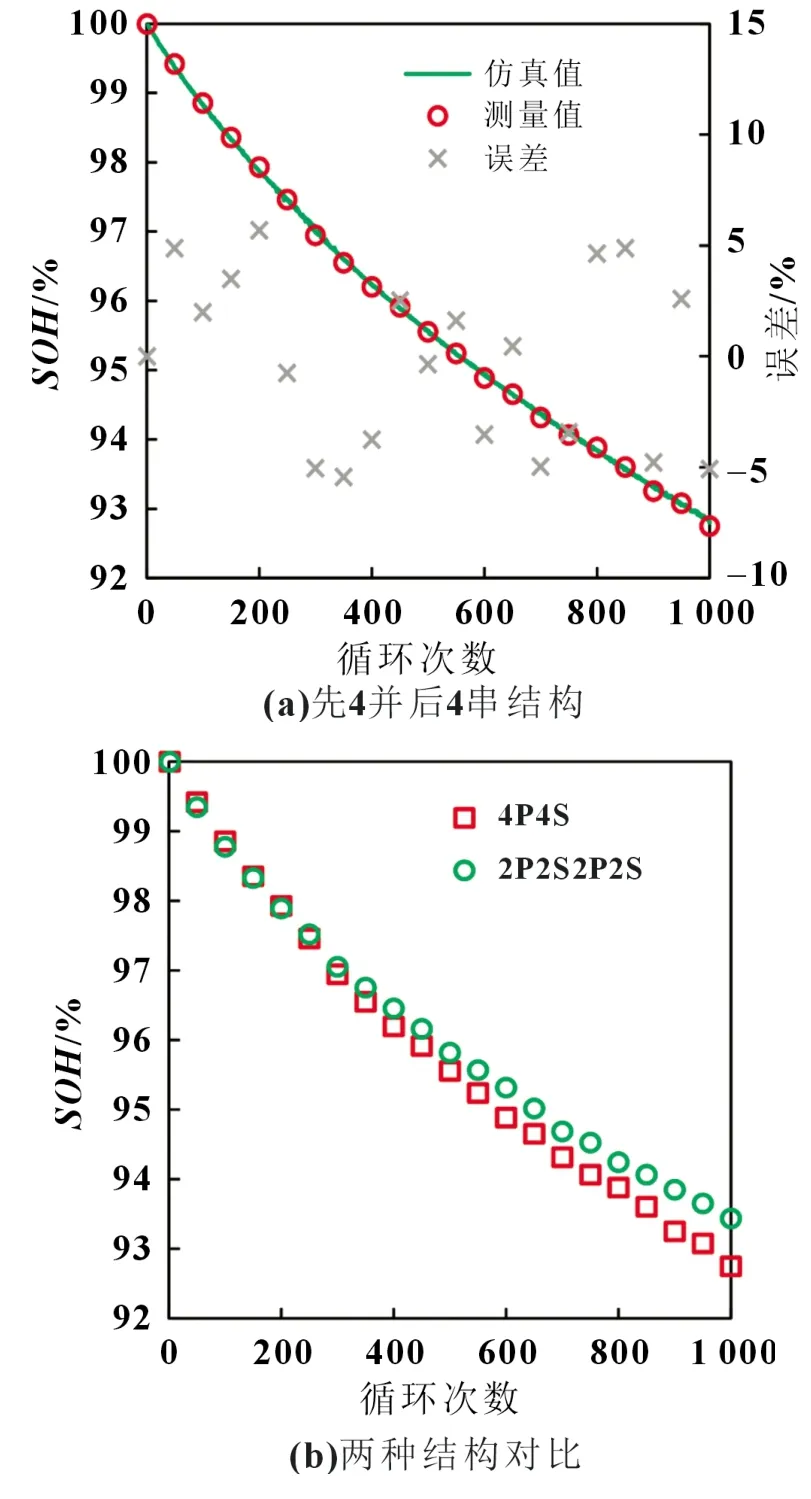
图8 磷酸铁锂电池组模型预测效果与误差

式中：C0为额定容量。

可以看出，所建模型在不同串并联结构下均具有良好的容量损失轨迹预测精度，整个老化过程中预测的最大误差与均方根误差分别控制在5%与3%以下，该实验结果证明了所提建模方法在预测容量损失轨迹方面的有效性；同时验证了基于本方法所得最优混联结构在老化速率方面，明显优于传统经典先并后串结构；进而证明了电池组串-并混联结构设计方法的有效性。

4 结论

为了获得给定电压、容量设计条件下循环寿命最优的串并联结构，本文分别从电池组老化行为建模与推衍预测两方面提出了面向循环寿命的最优电池组串并联结构选择方法。在电池组建模方面，在经典电池动态模型的基础上，添加对电池在短时间与长时间尺度下老化行为的描述，进而结合对组内不一致参数的描述，从而完成对电池组老化行为的刻画。在推衍预测方面，从囊括商用成组方式的典型结构出发，基于所述电池组建模方法构建典型结构并仿真以形成预测样本集；进而结合非线性推衍预测方法，得出所有结构的循环寿命，最终完成对最佳拓扑结构的标定。

为了验证所提模型与预测方法的效果，本文以磷酸铁锂/石墨电池为研究对象，在串并联数均为4的设计阵列下，对先4 并后4 串结构与先2 并2 串后2并2 串混联结构在1C/25 ℃、满充满放条件下分别进行了循环老化仿真分析与实验验证。结果表明：(1)所提电池组建模方法在不同串并联结构中均能以较高的精度预测容量损失轨迹；(2)所提推衍预测方法能较为准确地推衍预测所有结构的循环寿命，进而遴选出最佳的串并联结构。