基于明考斯基最优距离的不完美排错SRGM决策机制

张 策, 王金勇, 徐早辉, 江文倩, 白 睿, 李文毓, 王建远

(1.哈尔滨工业大学(威海) 计算机科学与技术学院 山东 威海 264209; 2.山西大学 自动化与 软件学院 山西 太原 030006; 3.中国科学院计算机网络信息中心 北京 100083; 4.华为技术有限公司 南京研究所 江苏 南京 210012; 5.哈尔滨工业大学 计算学部 黑龙江 哈尔滨 150006; 6.华为技术有限公司 苏州研发中心 江苏 苏州 215028)

0 引言

为了定量化地提高软件系统的可靠性,软件可靠性增长模型(software reliability growth model,SRGM)得到了深入的研究。基于对故障检测至修复过程的不同假设,目前所建立的可靠性模型有数百种,但并不存在一个能够适用于所有失效数据集和评测标准的模型。因此,如何评测SRGM的性能优劣从而选择合适的SRGM,成为当前研究中亟待解决的问题。

在SRGM的评价与选择机制上,文献[1]基于欧几里得距离进行SRGM的最优选择,通过计算模型与理想解之间的最短距离来确定最优者,但其缺少对更多评测性能标准的考虑。文献[2]从决策软件发布角度提出了在工程实际应用中选择SRGM的方法,其通过评价模型预测软件中剩余故障的准确性来进行SRGM的选择与评判。在多属性决策[3]方面,文献[4]通过MSE拟合标准和自定义的预测指标对SRGM进行评价,并给出了具体的SRGM选择执行流程。就整体而言,已有的研究仅孤立地比较SRGM的拟合性能,未考虑不同标准重要性的差异,也没有考虑测试过程中由于测试环境和测试策略的改变而引发的各种实际问题。由于软件公司对失效数据集的发布不具备及时性,发布的信息往往有限(通常只有测试时间、失效故障数量以及测试工作量[5-6]等),使得科研人员对基于失效数据集的SRGM研究具有被动性、滞后性和片面性。

笔者在前期工作中提出了统一的与不完美排错相关的SRGM[7],研究了不完美排错环境下的软件最优发布问题[8],并分析了不同的SRGM[9-10]性能存在差异的原因。本文从矩阵分析的角度对SRGM的性能评估与选择问题进行形式化描述,提出成本受限下的双最优化排序方法,建立基于明考斯基距离的SRGM决策机制,并给出SRGM间的性能偏序关系。在公开发表的真实失效数据集上的实验结果表明了所提出方法的有效性,可以为模型决策提供定量化的参考。

1 真实软件测试过程与可靠性模型

真实软件测试过程描述如图1所示。可以看出,真实的测试流程是执行测试策略、发现故障、分析原因、排错、检查,之后再执行测试策略的周期性过程。

随着测试的执行,故障不断地被检测和修复,从而使得软件可靠性得以逐渐提升。从研究的视角来看,科研人员希望能够定量地评定该过程结束时系统的可靠性。为此,需要从数学定量分析的角度对测试过程进行建模,得到主要变量之间的数值关系,为可靠性增长找到研究的突破口。相比于完美排错,不完美排错[11-12]是针对更加真实的测试过程的可靠性研究,包含了多种测试过程中的实际因素。在当前研究中,由于各个模型所做的假设有所不同,可以得到多种类型的可靠性模型。因此,需要选择出与实际工程特征相接近的可靠性模型作为预选集合。

图1 真实软件测试过程描述Figure 1 Description of the real software testing process

2 不完美排错软件可靠性模型决策

2.1 SRGM评价问题的形式化描述

设有K个SRGM模型构成集合M,M={Mi|1≤i≤K}={M1,M2,…,MK}, 其中模型Mi由拟合与预测两大类指标构成。

定义1评测指标。模型Mi有N个拟合指标Fi={fij|1≤j≤N},L个预测指标Qi={qik|1≤k≤L}, 1≤i≤K,这些评测指标是由K个模型在指定失效数据集上进行参数拟合后计算得到的。

K个SRGM模型的拟合标准值和预测标准值构成了评测决策矩阵D,

(1)

D是包含N+L个属性、K个方案的决策矩阵。为便于计算以及更加清晰地呈现模型间的数值差异,需要对D中的元素进行标准化处理。

7个拟合评测标准为MSE、MEOP、Variation、RMS-PE、TS、BMMRE和R-square,将这些标准值变换为[0, 1] 区间内正向增长的无量纲数值。

对于评测标准MSE、MEOP、Variation、RMS-PE、TS、BMMRE,

对于评测标准R-square,

式中:1≤j≤N+L。

对得到的评测数据进行标准化处理,

(2)

至此,可以得到标准化矩阵R,

(3)

(4)

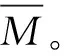
2.2 考虑双最优化距离的SRGM决策

基于式(4)的描述,可将K个模型抽象为K个节点N1,N2,…,NK。为了评测K个模型的性能差异,可以采用基于距离的SRGM决策方法,如图2所示。其中,N0节点表示理想解节点,是基于某种标准构造的用于衡量K个节点性能的节点,因此被标记为虚拟节点N0。

图2 基于距离的SRGM决策Figure 2 SRGM decision based on distance

采用明考斯基距离(Minkowski distance,MD)函数来度量不同模型(即对象)间的差异,

dk(i,j)=

(5)

式中:i=(xi1,xi2, …,xip)和j=(xj1,xj2, …,xjp) 是两个p维的数据对象;k是一个正整数,表示k重度量距离。

显然,明考斯基距离满足如下基本性质:d(i,j)≥0,d(i,i)=0,d(i,j)=d(j,i),d(i,j)≤d(i,k)+d(k,j)。这使得明考斯基距离可以用来度量不同节点间的差异。

当k=1时,d称为曼哈坦距离;当k=2时,d称为欧几里德距离。这里,考虑N+L个评测属性,令k=N+L,表示N+L维的距离度量。通常,在度量某节点的性能时,是通过计算该节点与最优评测标准构成的虚拟节点之间的距离来实施的,但这种评测方法不能保证一定有效。这是由于在多维空间中每个模型的标准所占有的权重并不一样,使得此多维空间不具备传统二维空间与三维空间的对称性,从而导致距离最优评测标准构成的虚拟节点最近的节点不一定距离最差标准构成的虚拟节点最远。为此,提出了双最优化排序方法(MMIMMD),用于度量不同模型(对象)间的差异,

(6)

式中:Np和Nq分别表示正向最优节点和负向最差节点,由评测标准中最优值和最差值的k维数据构成,即Np=(x1p,x2p,…,xkp),Nq=(x1q,x2q,…,xkq),其中:xip=max{xij|1≤j≤k},xiq=min{xij|1≤j≤k}, 1≤i≤K。

显然,D(Ni,Np)越小,表示节点Ni距离正向最优节点Np越近,评测模型性能的指标趋向较好;D(Ni,Nq)越大,表示节点Ni距离负向最差节点Nq越远,评测模型性能的指标趋向较好。

D(Ni,Np)和D(Ni,Nq)均采用明考斯基距离公式来计算,

1≤i≤K;

(7)

1≤i≤K。

(8)

D(Ni,Np)和D(Ni,Nq)均包含t时刻累积检测的故障数量表达式m(t),因此m(t)是可靠性模型研究的关键。

3 数值算例评价

3.1 SRGM实例与数据集

选取8个典型的不完美排错SRGM进行实验和评价分析,具体情况如表1所示。

表1 8个典型的不完美排错SRGMTable 1 Eight typical imperfect debugging SRGM

可靠性模型的验证集由公开发表的真实失效数据集来完成,这里选择4个实际计算机应用系统测试过程中记录的失效数据集DS1～DS4[18-21]来进行实验,这4个数据集已被广泛用来验证SRGM的性能。

3.2 SRGM的拟合曲线和RE预测曲线

将表1中的8个模型在4个数据集上进行参数拟合,基于拟合的参数数值得到模型的m(t)表达式,用以估计模型的性能表现。图3为不同模型的拟合度量曲线,展现了模型与真实失效数据集的接近程度。图4为不同模型的RE预测曲线,展现了模型对未来失效数据的预测能力,曲线越接近于零线表明其预测性能越优。

从图3可以看出,在不同的失效数据集上,部分模型曲线与真实的失效数据曲线发生较大程度重合,表明拟合性能较好;另一部分模型曲线则发生较大偏离,表明拟合性能并不理想。例如,在DS1上,SRGM1和SRGM6出现了明显偏差;在DS2上,SRGM1和SRGM4出现了明显偏差。

图3 不同模型的拟合度量曲线Figure 3 Fit metric curves of different models

从图4可以看出,不同模型的RE曲线或正偏向或负偏向趋近于零线,难以区分模型间的RE曲线性能。在DS3和DS4上,RE曲线都是在第16周之前发生较大幅度的波动并逐渐收敛,但相互之间的性能并不容易直接区分。

3.3 数据处理与结果分析

3.3.1数据处理 对于各模型在不同失效数据集上的性能指标进行归一化处理,形成[0,1]区间内的数值(由于篇幅原因,更多数据不再列出)。

3.3.2结果分析

1)权重设置

目前对可靠性模型的评测主要从拟合与预测两个方面进行,二者的重要性基本相同,故将拟合与预测的权重均设置为0.5。

在拟合指标上,相比MEOP、TS、RMS-PE和BMMRE标准,MSE、R-square和Variation标准被更广泛地用来衡量模型的拟合性能。因此,将后三者权重设定为前四者的两倍以示区别。预测指标RE权重设置与7个拟合指标权重相同。拟合与预测指标权重设置如表2所示。

此外,对比了带权重的最优节点距离与最差节点距离,分析了不同数据集下模型距离最优节点远近和距离最差节点远近这两种排序,发现单纯通过简单的模型优劣计算方法来评判模型性能会导致较大的偏差。

2)模型性能比较及权重的敏感性分析

采用本文提出的双最优化排序方法MMIMMD计算模型的性能排序,同时为了进行对比,也实现了

图4 不同模型的RE预测曲线Figure 4 RE prediction curves of different models

表2 拟合与预测指标权重设置Table 2 Settings of fitting and prediction weights

基于简单加权法与基于欧几里得距离法的模型性能排序。其中,简单加权法是依据加权平均值的大小进行排序;欧几里得距离法则是计算各个模型与理想解之间的最短距离来排序。表3给出了3种决策方法的排序结果。

为了观察不同拟合标准权重对模型性能排序的影响,取消了7个拟合标准的权重数值,得到表4所示的结果。可以看出,权重的设置会对模型的预测性能产生影响。例如,SRGM4模型在DS1上和SRGM8模型在DS2上,当无权重设置时双最优距离评估较好,有权重设置时双最优距离评估较差。但这并不是决定模型预测性能的最关键因素,因此这也证明了当前文献中多采用此标准的合理性。

3.4 讨论

3.4.1关于权重设置 对于刻画拟合性能的多个指标属性,以及除了RE以外更多的评价预测性能的指标属性,属性权重完全可以根据实际需要采用有关方法进行设置。例如,当认为拟合更重要时,可利用特征向量法、最小加权法或信息熵等方法来确定具体的拟合指标权重。

3.4.2关于真实工程环境下的决策 在大型的复杂软件测试过程中,选择合适的可靠性模型作为指导来提高可靠性,仍面临着更多的考验。例如,需要明晰整体测试策略,掌握测试过程的消耗情况(涉及对测试工作量变化的观测),确定故障检测数量的基本走势,据此再进行分类选择,这都会加重模型选择的难度。本文对此进行了初步探索,后续更为具体和深入的研究亟须加强。

3.4.3关于计算复杂性 趋近真实测试过程的可靠性模型往往包含大量的参数,具有较为复杂的表达式结构,观测模型更多的性能指标也会引发巨大的计算量,甚至超出人工能力范畴。针对上述情况,

表3 3种决策方法的排序结果Table 3 Ranking results of three decision methods

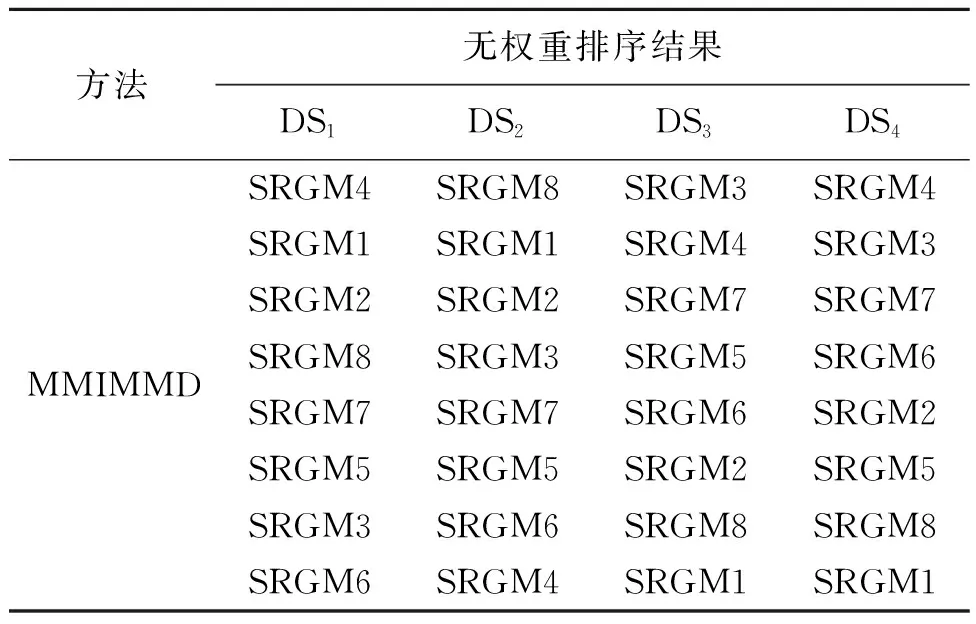
表4 MMIMMD决策方法的无权重排序结果Table 4 Ranking results without weight of MMIMMD decision method

需要借助具备复杂模型分析与处理的数值软件来完成,通常会进行近似计算处理,而这将成为一种普遍的现象。

4 结语

针对当前可靠性模型数量多以及难以实施有效决策的问题,提出了具体的SRGM选择方法。依据模型在拟合与预测两个方面的性能,建立基于明考斯基距离的双最优化排序模型,定量化地对模型性能进行标准归一化处理,建立模型间的偏序关系,从而实施有效决策。通过在公开发表的真实失效数据集上进行实验和分析,验证了所提出方法的有效性,为定量决策模型提供了有力支持。模型性能评价可以归属到多属性决策问题的范畴,对于偏好上的差异将直接影响决策结果。因此,通常需要设定一系列的决策条件并考虑模型的使用场景,选择合适的方法进行决策。后续研究中要区分测试环境与运行环境的差异性,依据用户的输入条件,充分利用模型性能的多类描述信息进行决策,采用不确定多属性决策方法(特别是随机多属性、模糊多属性和粗糙多属性等)进行决策,不断丰富研究内容。