基于卡尔曼滤波算法的风电机组动态推力消减控制策略

牛焕然，黄国燕，黄 蓉，胡 广，赵 森，董竹林

(明阳智慧能源集团股份公司，中山 528437)

0 引言

为了提高风电机组在中、低风速区域的发电效率，近年来其叶片设计逐渐向大型化发展，但随着风轮扫掠面积的增加，塔顶轴向受力水平显著增大，由风电机组推力导致的各部件极限荷载问题越来越突出。因此，如何降低风电机组关键部件的极限荷载，进而延长风电机组的寿命是近年来大型风电机组的重点研究方向[1-4]。

对于现代大型变速变桨式风电机组而言，由于其叶片特点，导致其运行于额定风速附近时，塔顶受到的推力显著增加，呈尖峰状；且风轮扫掠平面的轴向推力也显著增加，使风电机组各部件遭受更大的极限荷载冲击，此种情况在极端风切变和极端阵风运行工况下更为严重[5-7]。如果不采取特殊的控制策略将严重影响风电机组各部件的安全及设计寿命。

目前针对风电机组在额定风速附近的推力控制策略，国内外大多采用测量风力发电机输出功率来间接反映推力变化趋势的方式，进而制定相应的变桨策略，以降低极限荷载对风电机组的危害[8]。但由于风力发电机输出功率与风轮扫掠平面轴向推力并不具备强关联性，因此，在实际应用中为了达到更好的推力消减和荷载降低效果，通常将风电机组的变桨范围设置的很宽，这将会导致风力发电机输出功率波动增大和风电机组发电效率降低等问题。因此，以测量风力发电机输出功率来间接实现推力消减的控制策略具有一定的局限性。

针对上述问题，本文在风电机组基本控制策略基础上，提出一种基于卡尔曼滤波算法的风电机组动态推力消减控制策略(下文简称为“动态推力消减控制策略”)，以减小风电机组在额定风速附近运行时的轴向推力，从而达到降低风电机组关键部件极限荷载的目的；最后以5.0 MW风电机组为例搭建半实物仿真实验平台，对所提出的控制策略进行实验验证。

1 变速变桨式风电机组的基本控制策略

风电机组实际吸收的等效功率Pe可表示为：

式中：ρ为空气密度；λ为叶尖速比；r为风轮半径；v为轮毂风速；β为桨距角；Cp为风能利用系数。

定义叶尖线速度和风速的比值为叶尖速比，则式(1)可表示为：

式中：ω为风轮转速；Kopt为最优运行模式下的增益。

则风力发电机最优运行模式下的转矩T可表示为：

风电机组风能利用系数曲线示意图如图1 所示。图中：λopt为最优叶尖速比；Cp,max为最大风能利用系数。

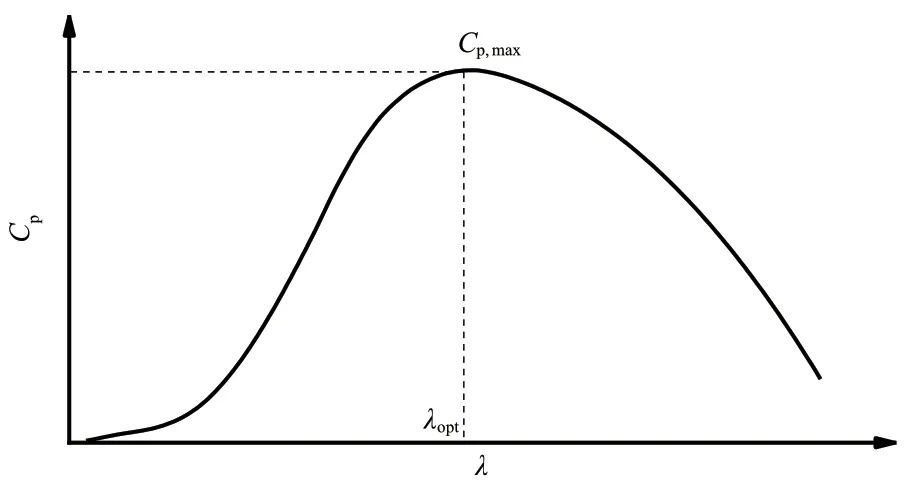
图1 风电机组风能利用系数曲线示意图Fig. 1 Schematic diagram of wind energy utilization coefficient curve for wind turbines

由图1 可知：当风电机组正常发电运行时，在最优桨距角下存在最大风能利用系数和与之对应的最优叶尖速比；同时，随着叶尖速比的增加或减小，风能利用系数逐渐降低。因此，为了提高变速变桨式风电机组的发电效率，需尽可能使风电机组长时间运行于最优叶尖速比附近，以确保其保持最佳的风能捕获能力[9-14]。

风电机组基本控制策略下的转矩-转速曲线如图2 所示。图中：ω1为最小风轮转速；ωr为额定风轮转速。

图2 风电机组基本控制策略下的转矩—转速曲线Fig. 2 Torque-speed curves under basic control strategy of wind turbines

从图2 可以看出：当风电机组维持在并网情况下的最小风轮转速时，随着风轮转速的增加，转矩逐渐增加至最优转矩后进入最优转矩控制阶段；此时风电机组在最优运行模式下运行，风力发电机转矩按式(3)确定，以保证风电机组始终在最佳叶尖速比下运行；当风轮转速达到额定转速时，风力发电机转矩由转矩比例-积分-微分(PID)控制器控制；随着风轮转速进一步增加，风电机组进入恒功率运行状态，转矩PID 控制器通过变桨动作减小风电机组的风能捕获效率，从而维持风电机组输出功率和风轮转速的稳定[15-18]。

2 基于卡尔曼滤波算法的风电机组状态估计

卡尔曼滤波算法是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法[19]。对于一个特定的线性系统[19-21]，其应满足：

式中：xk、xk-1分别为k、k-1 时刻的计算值；uk-1为k-1 时刻的输入矢量；ωk-1为k-1 时刻的预测过程白噪声；zk为k时刻的测量值；vk为k时刻的观测过程噪声；A、B、H分别为风速估计状态空间矩阵的状态转移矩阵、过程矩阵和量测矩阵。

卡尔曼滤波器的时间更新方程可表示为：

式中：为k-1 时刻的预测值。

式中：为k时刻的先验估计值；为k时刻的先验估计协方差；Pk-1为k-1 时刻的协方差；Q为过程噪声矩阵。

由式(5)、式(6)可知：基于卡尔曼滤波算法的最优状态估计是利用上一时刻估算值和当前时刻的协方差估计值对当前时刻结果进行最优估计，即用测量数据对状态预测结果进行实时纠正。

卡尔曼滤波器的状态更新方程可表示为：

式中：为k时刻预测值；M为测量噪声矩阵；Kk为k时刻卡尔曼滤波增益；Pk为k时刻协方差；定义k时刻测量值与先验估计值的差zk-为新息。

k时刻的先验估计值、卡尔曼滤波增益和新息共同修正k时刻的预测值，由式(8)可知，当卡尔曼滤波增益值为零时，k时刻的预测值等于先验估计值，说明估计结果更信任预测值；随着卡尔曼滤波增益值的增加，预测结果将更依赖测量值，可以看出卡尔曼滤波算法通过实时更新协方差矩阵和卡尔曼滤波增益对预测值进行实时校正。

基于卡尔曼滤波算法的风速估计状态空间矩阵可分别表示为[22]：

式中：Ddt、Kdt分别为传动系统的等效弹性刚度和阻尼系数；Jr、Jg分别为风轮和风力发电机的转动惯量；G为齿轮箱传动比。

风电机组输入矢量u=[Ta,Tg]T，状态估计矢量x=[ω,ωg, Δθ]T，其中，Ta、Tg分别为低速轴和风力发电机的转矩；ωg为风力发电机的转速；Δθ为低速轴的等效扭转角[23-25]。

3 风速估计模型

基于卡尔曼滤波算法的风速估计原理如图3所示。图中：PKF为最优估计功率值。

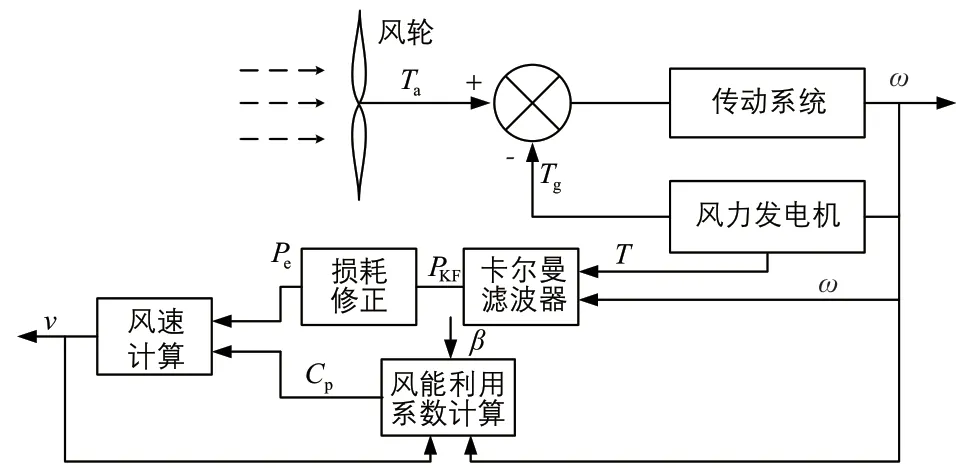
图3 基于卡尔曼滤波算法的风速估计原理图Fig. 3 Schematic diagram of wind speed estimation based on Kalman filtering algorithm

由图3 可知：低速轴转矩与风力发电机转矩共同作用于传动系统，随着外界风况的变化，将在传动系统中产生一个变化的风轮转速。以测量的转矩和转速为输入量进行卡尔曼滤波最优状态估计，对最优估计功率值进行损耗修正，实时计算出风电机组实际吸收的等效功率，同时通过测量的风电机组风轮转速和前一时刻风速估计值，计算出风电机组叶尖速比。

风电机组风能利用系数曲线3D 图如图4 所示。

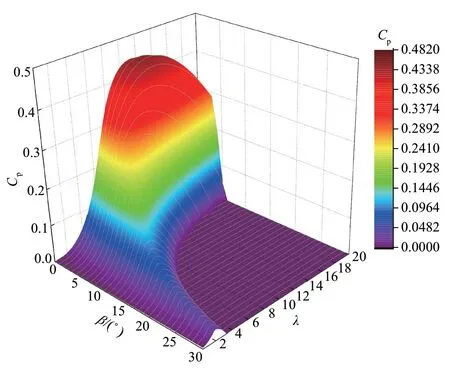
图4 风电机组风能利用系数曲线3D 图Fig. 4 3D plot of wind energy utilization coefficient curve for wind turbines

从图4 可以看出：在不同叶尖速比和不同桨距角下，风电机组的风能利用系数最大值存在较大差异，整体趋势为随着桨距角的增加，风能利用系数最大值逐渐减小。风能利用系数是关于桨距角和叶尖速比的二维矢量，该数据可由风电机组模型的静态数据获得。通过计算的风电机组实时叶尖速比和测量的实际桨距角位置，对风能利用系数进行计算；最后通过式(1)由风电机组实际吸收的等效功率和当前风能利用系数对风电机组风速进行估算。

4 动态推力消减控制策略

风电机组在正常发电运行期间，其轴向推力F可表示为：

式中：Ct为叶片推力系数，是关于叶尖速比和桨距角的二维矩阵。

叶片推力系数曲线3D 图如图5 所示。

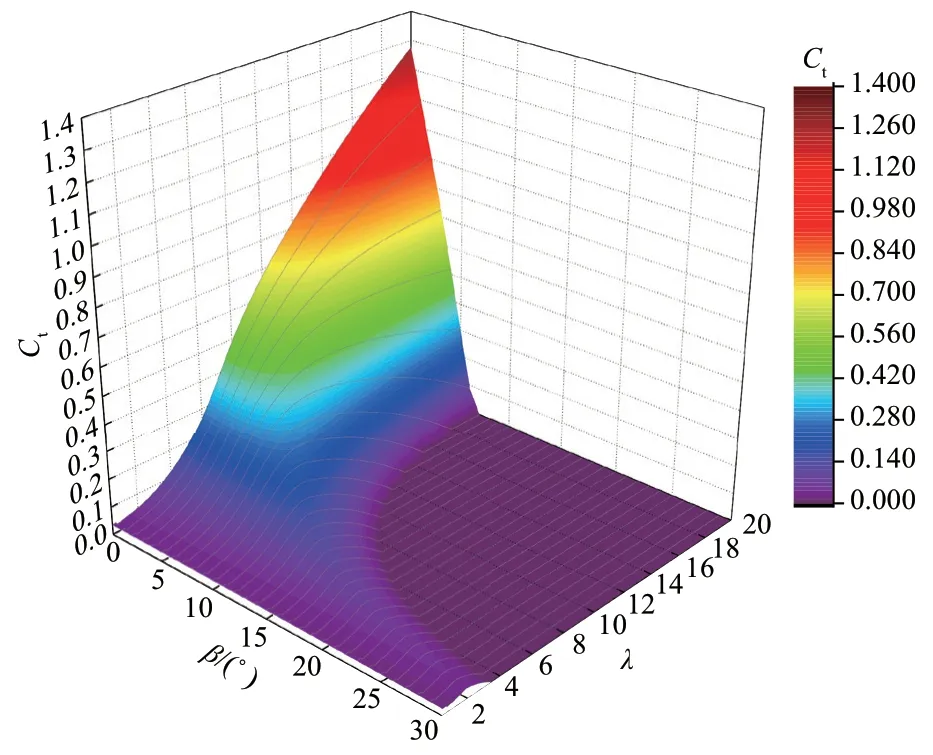
图5 叶片推力系数曲线3D 图Fig. 5 3D plot of blade thrust coefficient curve

从图5 可以看出：在相同叶尖速比下，叶片推力系数随着桨距角的增加而减小，即随着桨距角的增加，风电机组的风能利用系数和轴向推力逐渐减小。

结合式(13)可知，对于某一台确定的风电机组，其轴向推力仅与轮毂风速和叶片推力系数相关，对于定桨距风电机组而言，由于桨距角固定，轴向推力随着轮毂风速的增大而增加；而对于变速变桨式风电机组而言，随着轮毂风速的增加桨距角增大，导致叶片推力系数逐渐降低。因此，不同于定桨距风电机组，变速变桨式风电机组的轴向推力将在额定风速附近出现峰值。风电机组轴向推力示意图如图6 所示。

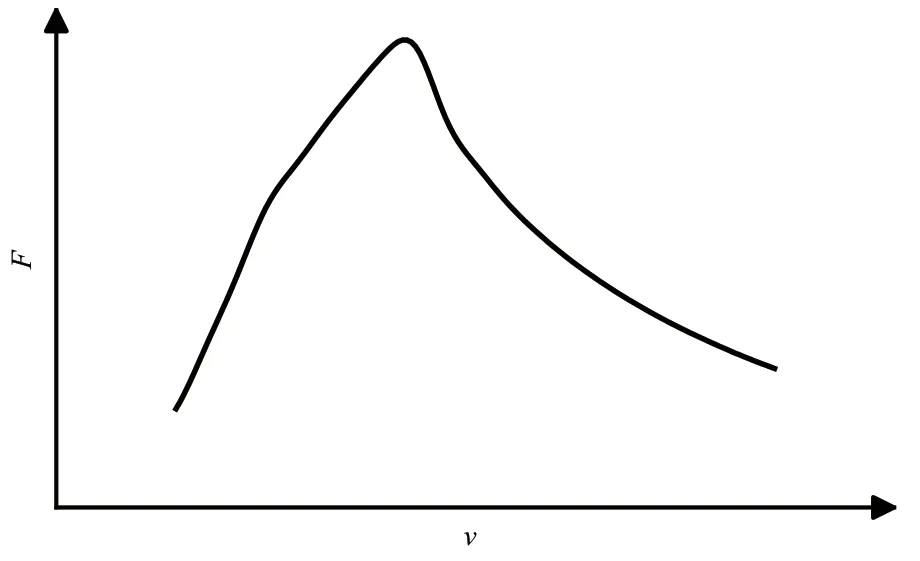
图6 风电机组轴向推力示意图Fig. 6 Schematic diagram of axial thrust of wind turbines

由图6 可以看出：当风电机组运行于额定风速附近时，其受到的轴向推力显著增加呈尖峰状，表现为叶片变形量增大，叶尖至塔筒最小距离减小，塔筒前后晃动位移增加。这不仅增加了叶片扫塔的风险，还会引起叶片、塔架等关键部件极限荷载和疲劳荷载的激增，严重影响机风电组的运行安全，缩短其使用寿命。

为减小额定风速附近风电机组所受轴向推力，本文对变速变桨式风电机组基本控制策略进行了优化，提出了动态推力消减控制策略，该控制策略流程图如图7 所示。图中：βmin为风电机组的动态最小桨距角。

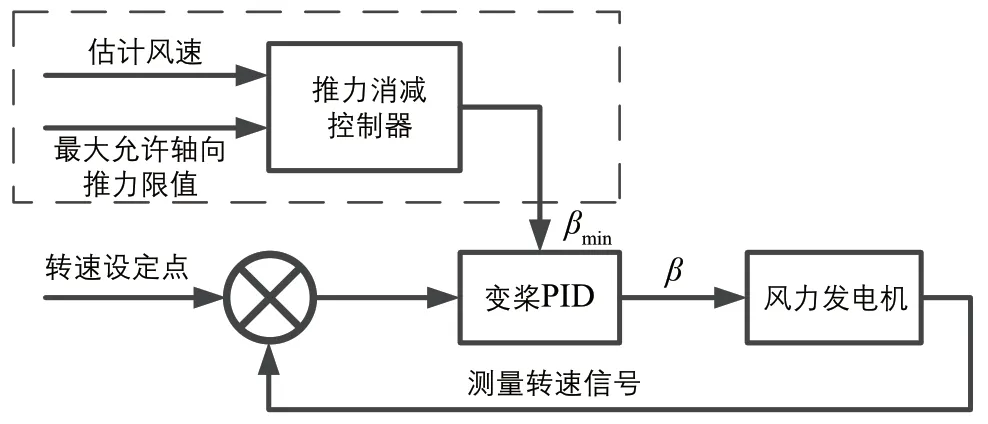
图7 动态推力消减控制策略流程图Fig. 7 Flowchart of dynamic thrust reduction control strategy

动态推力消减控制策略的基本原理为：利用上文估算得到的风速值，通过式(13)实时计算出对应风速下的叶片推力系数，并通过Ct(λ,β)二维矢量计算出满足最大允许轴向推力限值的最优桨距角；之后将推力消减控制器计算得到的最优桨距角定义为风电机组的动态最小桨距角，并其作为变桨PID 的最小桨距角限制；最后通过变桨控制器将桨距角需求传递给风电机组执行模块，以实现其轴向推力消减控制。

5 实验验证分析

本文以某5.0 MW 风电机组为例，搭建了半实物仿真实验平台，利用其对所设计的动态推力消减控制策略进行实验验证。搭建的风电机组半实物仿真实验平台如图8 所示，基于风电仿真软件Bladed Hardware Test 的硬件仿真模块实现可编程逻辑控制器(PLC)，即主控制器和Bladed Hardware Test 软件的数据交互。在Bladed Hardware Test软件中通过配置IP地址、测试脚本、通信协议和数据通道后生成“.plan”格式的文件，并将文件导入到Bladed Hardware Test 软件中，完成上述设置后进行半实物仿真实验。需要说明的是，本实验中额定风速取10.4 m/s。

图8 风电机组半实物仿真实验平台Fig. 8 Wind turbine hardware in the loop simulation experiment platform

5.1 动态推力消减控制策略对稳态风时的轴向推力及荷载的影响

采用考虑垂直风切变的稳态风模型，同时设置风速步长为0.5 m/s，在不同控制策略下进行半实物仿真实验验证。稳态风时不同控制策略下的轴向推力弯矩变化特点如图9 所示。其中：开启推力控制是指采用动态推力消减控制策略；禁用推力控制是指关闭动态推力消减控制策略，即采用风电机组基本控制策略。后文同此。

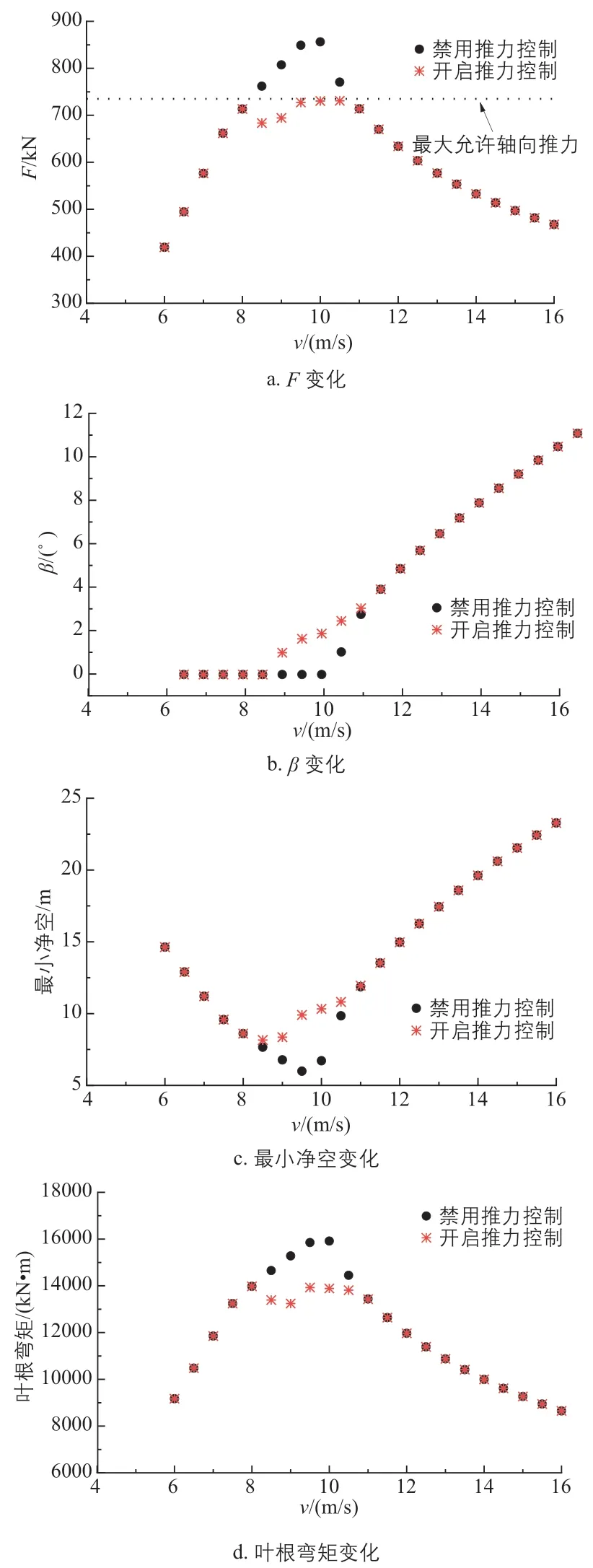
图9 稳态风时不同控制策略下的轴向推力及弯矩变化特点Fig. 9 Axial thrust and bending moment variation characteristics under different control strategies during normal wind

从图9 可以看出：

1)禁用动态推力消减策略时，风电机组的轴向推力最大值为856.31 kN；而采用动态推力消减控制策略时，在推力增加时，该策略通过实时下发桨距角需求来确保风电机组轴向推力最大值始终在设定值附近波动，以削弱风电机组在额定风速附近的尖峰推力，其轴向推力最大值仅为730.73 kN，相较于禁用动态推力消减策略时降低了14.67%。

2)采用动态推力消减控制策略时，最小净空(即叶尖与塔架的最小距离)增加了2.17 m。

3)采用动态推力消减控制策略时，叶根弯矩降低了12.17%。

综上可知，动态推力消减控制策略可显著降低风电机组整机静态荷载，提升其安全性。

5.2 动态推力消减控制策略对湍流风时的轴向推力及荷载的影响

湍流风时不同控制策略下的轴向推力及弯矩变化特点如图10 所示。

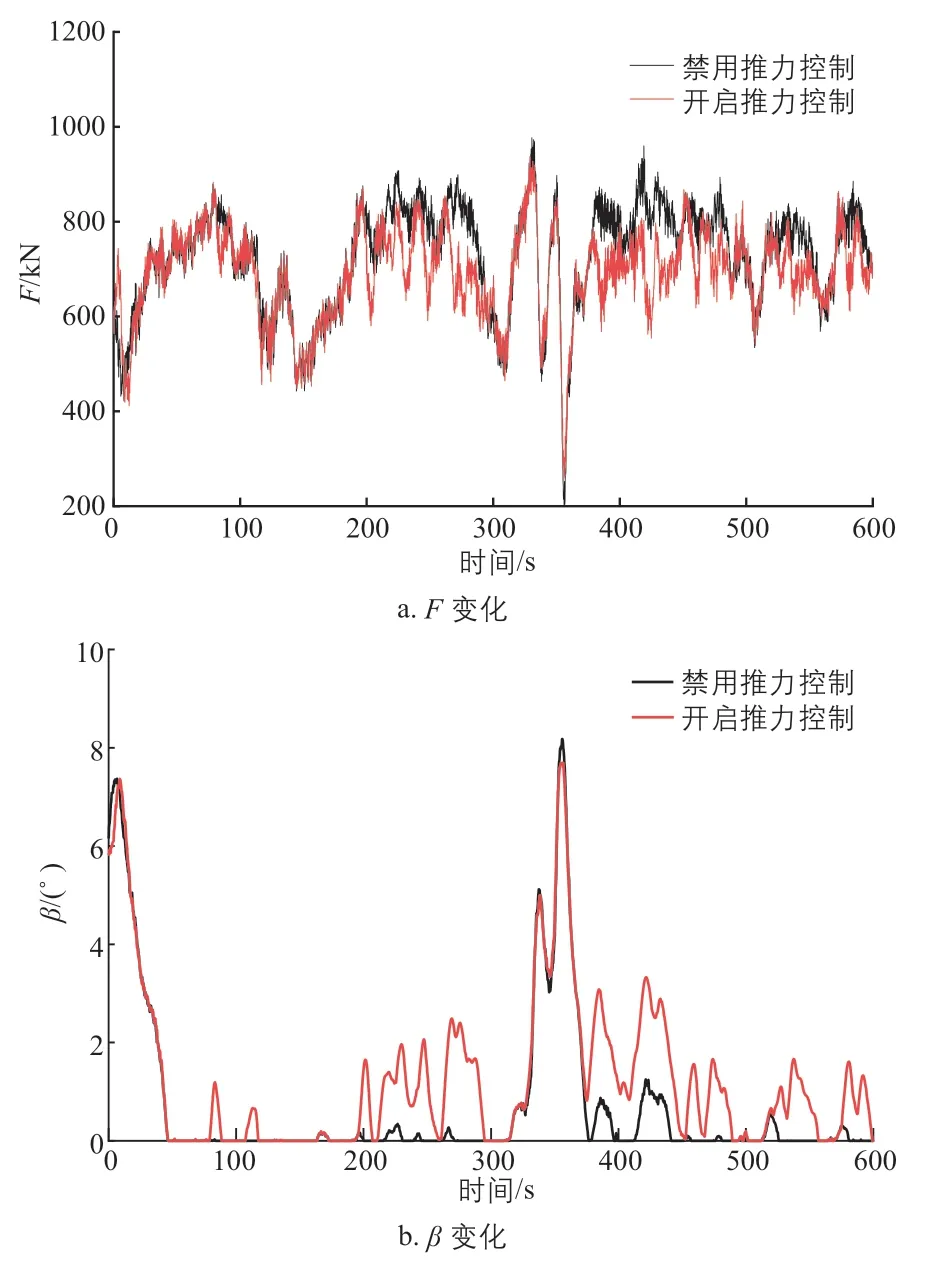
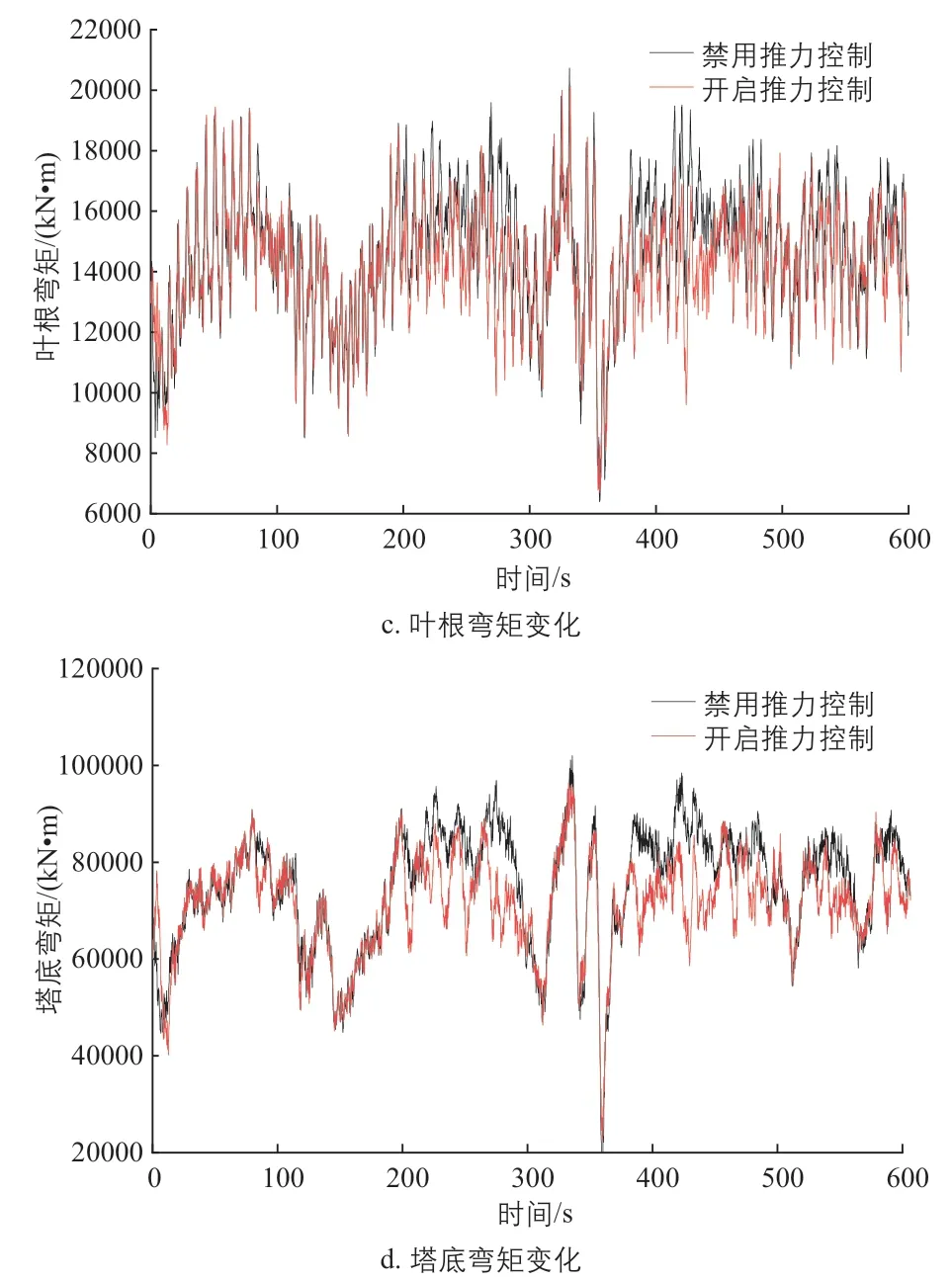
图10 湍流风时不同控制策略下的轴向推力及弯矩变化特点Fig. 10 Axial thrust and bending moment variation characteristics under different control strategies during turbulent wind

由图10 可知：当采用动态推力消减控制策略时，在额定风速附近推力削减效果明显，最大轴向推力比禁用动态推力消减控制策略时降低了4.5%，叶根弯矩降低了2.85%，塔底弯矩降低了5.5%。由此可知，该控制策略可显著降低湍流风工况下的风电机组荷载。

6 结论

本文在风电机组基本控制策略基础上提出了一种基于卡尔曼滤波算法的动态推力消减控制策略，根据风电机组能量传递关系，以测量转矩、桨距角和风轮转速为输入量，对轮毂风速进行估计，经过推力消减控制器的最优桨距角计算实现动态变桨，以降低风电机组整体的轴向推力水平；最后以某5.0 MW 风电机组为例，搭建了半实物仿真实验平台，对提出的控制策略进行了实验验证。实验结果表明：该控制策略能够有效降低风电机组轴向推力，减小风电机组极限荷载。