基于ADE-PML方法的快速计算目标电磁场分布研究

叶文娟

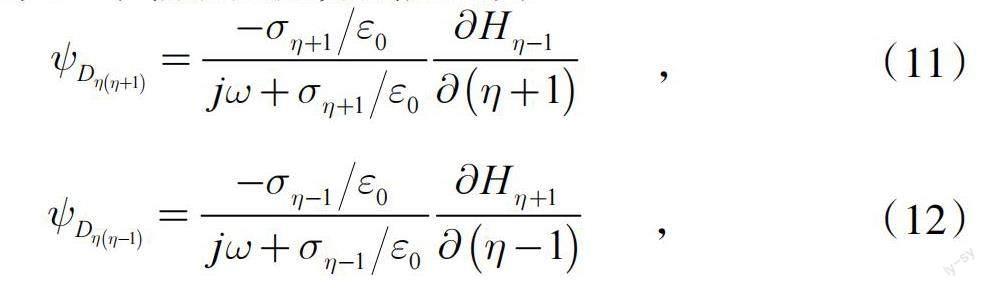
摘  要：在电磁场分布计算领域，目标的电磁分布计算是一个重要且复杂的问题。目前，常用的计算方法有有限元法、有限差分法、时域积分方程法等。这些方法都有各自的优缺点，但是无论哪种方法都需要进行离散化、求解和后处理等，存在计算量大、计算时间长、计算精度低等问题。为了解决这些问题，一些新的计算方法被提出，如自适应离散化误差修正技术，自适应边界条件技术等。这些技术能够有效地提高计算精度和计算效率，但是在具体工程应用中，仍然存在一些问题，例如处理复杂目标的电磁场分布计算难度仍然较大、计算时间较长等。通过基于ADE-PML方法研究快速计算复杂目标的电磁场分布，进一步提高电磁场分布计算效率，有助于复杂目标电磁分布工程应用分析。

关键词：ADE-PML；快速；电磁场；分布；计算效率

中图分类号：TM412      文献标志码：A          文章编号：2095-2945（2024）05-0012-04

Abstract： In the field of electromagnetic field distribution calculation， the calculation of the electromagnetic distribution of targets is an important and complex problem. Currently， commonly used calculation methods include finite element method， finite difference method， and time-domain integral equation method， among others. These methods have their own advantages and disadvantages， but all require discretization， solving， and post-processing， thus resulting in large computational workload， long computation time， and low computational accuracy. In order to solve these problems， new calculation methods have been proposed， such as adaptive discretization error correction techniques and adaptive boundary condition techniques. These techniques can effectively improve computational accuracy and efficiency. However， in practical engineering applications， there exist some challenges， such as the difficulty in handling the electromagnetic field distribution calculation of complex targets and long computation time. By studying the fast calculation of electromagnetic field distribution of complex targets based on the ADE-PML method， it is possible to further improve the efficiency of electromagnetic field distribution calculation for complex target engineering applications.

Keywords： ADE-PML; fast; electromagnetic field; distribution; computational efficiency

电磁场分布计算是电磁学领域中一个非常重要的问题，涉及电磁场的产生、传播和相互作用等方面。电磁场分布计算方法发展主要分为解析阶段、数值阶段、混合階段和近似阶段。解析阶段通常只能计算简单目标和边界条件；数值阶段可以对结构和材料近场进行计算，但是计算精度和计算效率往往是其矛盾的2个方面；混合阶段适用于局部复杂性的问题，并一定程度上能够提高计算精度和计算效率；近似阶段往往可以计算复杂目标的几何结构和边界条件，但是其计算精确的电磁场分布一般比较困难。

结合近似阶段各种方法的优点，一定程度上克服计算精度的不足，研究ADE-PML计算方法能够快速准确地计算目标的电磁场分布。此方法可用于各种不同的应用领域，例如电力系统、电机设计、暗室设计等，有效分析电磁场的分布和特性并优化设计方案，进一步提高产品性能。

1  电磁场分布计算的常用方法

在电磁场分布计算中，常用的方法包括有限元法、有限差分法、边界元法和有限积分法等。

有限元法（Finite Element Method，FEM）是一种常用的数值计算方法，其将求解区域划分为许多小的有限元单元之间的关系，利用数学模型和适当的边界条件，通过求解线性或非线性方程组来获得电磁场分布。有限元法适用于各种复杂的电磁场问题，如静电场、静磁场、电磁波转播等。

有限差分法（Finite Difference Method，FDM）是一种基于差分逼近的数值计算网格，其将求解区域划分为网格，将偏微分方程中的导数用差分近似代替，建立差分方程组，通过迭代求解来得到电磁场分布。有限差分法适用于各种电磁场问题，如静电场、静磁场、电磁波传播等。

边界元法（Boundary Element Method，BEM）是一种基于边界积分方程的数值计算方法，其将求解区域划分为边界和内部2个部分，通过在边界上建立边界积分方程，将未知量从内部转移到边界上，通过求解边界积分方程组来获得电磁场分布。边界元法适用于具有边界条件的电磁场问题，如静电场、静磁场。

有限积分法（Finit Integration Technique，FIT）是一种基于有限差分和有限元的方法，其将求解区域划分为网格，通过在每个网格中应用电磁场的积分形式，建立离散的方程组，通过求解方程组来得到电磁场分布。有限积分法适用于各种电磁场问题，如静电场、静磁场、电磁波传播等。

除了上述几种方法，还有模态分析法、时域有限差分法、时域积分方程法等，在不同应用领域和问题上有着不同的优势和适用性。

2  ADE-PML计算原理

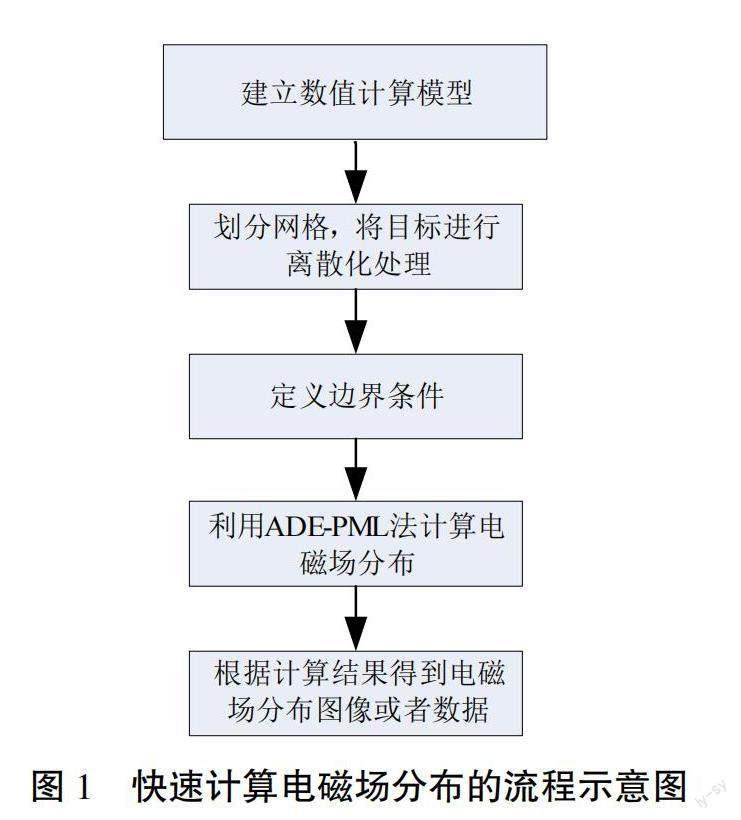
ADE-PML是一种用于求解时域麦克斯韦（Maxwell）方程组的数值方法，其中ADE是交替方向显式（Alternating Drection）方法，PML代表完美匹配层（Perfectly Matched Layer）。该方法主要用于模拟电磁波在复杂介质中的传播和散射现象，例如雷达、天线、光纤通信等领域。ADE-PML的主要思路是将麦克斯韦方程组分解为3个方向的单一维度问题，然后采用交替方向显式法进行求解。同时，为了避免边界反射和波导效应，采用完美匹配层技术对边界进行处理，使得边界处的电磁波能够被吸收，从而得到更准确的解。ADE-PML方法具有计算精度高、计算速度快、适用于复杂介质等优点，被广泛应用于电磁场计算、天线 、光纤通信等领域。利用ADE-PML法快速计算目标电磁场主要包括5个步骤，具体如图1所示。

2.1  建立数值计算模型

建立目标的电磁计算模型，包括目标的几何形状、材料参数、边界条件。其中，几何形状是明确计算目标的物理形状和尺寸以建立计算模型的实体；材料参数是明确计算模型的传输特性，主要是模型的材料电磁参数，包括介电常数、磁导率和电导率；边界条件是一种能够有效吸收入射波的边界条件，需要设置合适的吸收层参数，如吸收层的厚度、吸收层的介电常数和磁导率等。

2.2  目标离散化处理

将计算区域划分为若干小区域，每个小区域称为一个网格。在划分网格后，采用自适应离散化误差修正技术对模型进行离散化处理，然后采用时间域有限差分法并根据时间步长进行时间域上的离散化处理后计算，得到离散化的计算模型。

基于辅助微分方程方法的PML公式及时域有限差分法（FDTD）计算域的电磁特性，在用于截断广义介质FDTD计算域的三维PML区域，麦克斯韦方程组中的2个旋度方程在频域的表达式为

式（1）、式（2）中，电位移矢量D与电场强度E、磁通量密度B与磁场强度H之间的本构关系为

式中：εr（ω）和μr（ω）分别是FDTD计算域介质的相对介电常数和相对磁导率系数，操作符▽s定义为

式中：Sη（η=x，y，z）是坐标拉伸变量，定义为

在三维笛卡尔坐标系中，式（1）和式（2）的分量形式为

基于辅助微分方程方法的PML算法如下，利用上述部分计算公式展开，由式（6）可以将S转化为

将式（9）代入式（7）中，得出

式中：2个辅助变量分别定义为

式（11）和式（12）可以改写为

利用傅里叶变换关系jω??/?t，可以将式（10）、式（13）、式（14）由频域变换到时域，即

采用标准的FDTD算法，在空间和时间上均使用中心差分格式，可以将式（15）—式（17）离散为

式（18）—式（20）中，

2.3  定义边界条件

在计算区域的边界上定义吸收边界条件为PML。

2.4利用ADE-PML方法计算电磁场

利用ADE-PML方法计算电磁场在每个时间步长和空间单元的数值。第一步是确定计算区域的网格大小和时间步长，网格大小需同时兼顾计算精度和计算量；时间步长必须小于空间步长除以介质中电磁波的最大传播速度。第二步是初始化电磁场，根据第一步的条件初始化电场和磁场。第三步是根据麦克斯韦方程通过差分分别计算出电磁和磁场在下一个时间步长的数值；第四步是重复以上步骤直到求解收敛，即电磁场的计算误差达到预设的精度要求。

2.5  计算结果显示分析

根据计算结果进行后，得到目标的电磁场分布图像或数据。

3仿真计算结果分析

为了验证本研究动态显示算法的有效性，利用上述理论基础编写仿真计算程序，并通过实际计算电磁波在自由空间中传播的场分布。激励源设置如图2所示，边界设置如图3所示，计算结果如图4所示。

通过图4可以看出，在计算时间为10 s左右时x方向上的电场分布可以非常直观地呈现。这将虚无缥缈的电磁场分布用等位线图直观地展示出来，供技术人员分析。

4  结论

本文介绍了采用ADE-PML方法计算电磁场并直观显示。通过分析ADE-PML的基本原理和实现方法，综合精度计算要求，阐述了目标电磁场分布计算的直观顯示过程，并通过实验仿真验证了该方法的可行性和有效性，该方法可在通信、雷达、微波、天线等领域为工程师提供便捷、高效的计算和分析方法。

参考文献：

[1] TAFLOVE A， HAGNESS S C. Computational Electrodynamics： The Finite-Difference Time-Domain Method 3nd[M]. Norwood， MA： Artech House，2005.

[2] TAFLOVE A. Advances in Computational Electrodynamics： The Finite-Difference Time-Domain[M].Boston： Artech House，1998.

[3] NAMIKI T. A new FDTD algorithm based on alternating-direction implicit method[J].IEEE Transactions on Microwave Theory and Techniques，1999， 47（10）：2003-2007.

[4] NAMIKI T. 3-D ADI-FDTD method unconditionally stable time-domain algorithm for solving full vector Maxwell's equations[J]. IEEE Transactions on Microwave Theory and Techniques，2000， 48（10）：1743-1748.

[5] SHIBAYAMA J， MURAKI M， YAMAUCHI J， et al. Efficient implicit FDTD algorithm based on locally onedimensional scheme[J].Electronics Letters，2005，41（19）：1046-1047.

[6] BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics，1994，114（2）：185-200.

[7] BERENGER J P. Three-dimensional perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics，1996，127（2）：363-379.

[8] AHMED I， KHOO E H， LI E P. Development of the CPML for three-dimensional unconditionally stable LODFDTD method[J].IEEE Transactions on Antennas and Propagation，2010，58（3）：832-837.

[9] RAMADAN O. Second-order split-step envelope PML algorithm for 2D FDTD simulations[J].Electronics Letters，2007， 43（15）：792-793.

[10] RAMADAN O. Complex envelope six-stages split-step PML algorithm for open region electromagnetic problems[J].IEEE microwave and wireless components letters，2008，18（11）： 713-715.

[11] LI J X， JIANG H L. Effective CNAD- and ADE-based CFS-PML formulations for truncating the dispersive FDTD domains[J].IEEE Antennas and Wireless Propagation Letters.2015，14：1267-1270.

[12] LI J， SHI X， JIANG H. 2-D unconditionally stable CFS-PML based on CNDG for truncating unmagnetized plasma media[J].IEEE Microwave and Wireless Components Letters，2017，27（4）：323-325.

[13] LI J， WU P， JIANG H. Implementation of higher order CNAD CFS-PML for truncating unmagnetised plasma[J].IET Microwaves， Antennas & Propagation，2019，13（6）：756-760.

[14] JIANG H L， ZHANG J F， JIANG W X， et al. Unconditionally stable CN-PML algorithm for frequency-dispersive left-handed materials[J].IEEE Antennas and Wireless Propagation Letters，2017，16：2006-2009.