复杂固-液介质的速度应力方程三角形单元间断伽辽金地震波模拟算法
2024-02-04曹文忠张伟
曹文忠,张伟
1 中国地震局地球物理研究所,北京 100081 2 南方科技大学地球与空间科学系,广东深圳 518055
0 引言
地震波数值模拟方法是地球物理学研究的重要领域之一,尤其是计算机技术的飞速发展,使其发挥了越来越重要的作用.近些年来,随着海底地震仪和光纤地震仪技术的发展,海洋地震学受到了越来越多的关注.构造活动频繁的区域是地震学研究的重点地区,构造活动会导致海底地形较为复杂.因此,准确高效的大规模复杂固-液介质地震波模拟方法在海洋地震学研究中将会具有非常大的潜在应用价值.
目前已经有多种数值模拟方法应用于地震波传播模拟问题中,不同的数值模拟方法各自具有优势,根据需要模拟的实际问题选择合适的方法.对于复杂固-液介质地震波数值模拟问题,需要显式施加边界条件才能确保模拟结果的准确,因此所使用的方法可以灵活的刻画复杂的固-液界面的形状,同时还应该易于施加固-液边界条件.
有限差分法(Graves,1996; Yang et al.,2006; 祝贺君等,2009; Lisitsa and Vishnevskiy,2010; Sun et al.,2019; Zhang and Zhang,2022) 计算效率高,易于并行求解,是目前地震波数值模拟中使用最广的方法之一.但是其采用结构化网格,存在复杂形状固液界面时,贴合界面生成网格的难度较大.同时,高阶格式下需要较宽的差分模板,在施加边界条件时,采用降阶处理会降低整体格式精度 (Zhang et al.,2014; Sun et al.,2016).Simultaneous-Approximation-Term Summation-By-Parts (SAT-SBP)格式通过单边差分施加边界条件,避免了整体格式精度降低的问题(Sun et al.,2020; 杨在林等,2020),但是仍然存在复杂结构网格生成耗时的问题.有限元法(Bao et al.,1998)采用非结构网格,可以灵活处理复杂几何固液边界.高阶格式时的有限元法求解需要对大型稀疏矩阵求逆,当网格数量较大时,内存需求高且并行求解存在难度.使用四边形或六面体单元的谱元法(Komatitsch and Vilotte,1998; Komatitsch et al.,2000,2002)解决了有限元法中高阶格式时并行求解的问题,但是只能使用四边形或六面体网格,对于复杂水体结构,仍然存在网格生成困难的问题.有限体积法(Tadi,2004)可以使用非结构网格单元,相邻网格单元直接使用通量进行连接,这种方式易于施加复杂边界条件.但是,有限体积法的模拟精度较低(Dumbser et al.,2007a),目前在地震波数值模拟中使用的较少.间断伽辽金法(Käser and Dumbser,2006)可以看作是有限元法和有限体积法的结合,单元之间采用通量的方式进行波场的传递,虽然增加了部分计算量,但是使得每个单元的求解可以独立,易于施加边界条件和并行求解.单元内部使用有限元的基函数,可以在三角形或四面体单元时采用高阶格式.间断伽辽金法非常适用于含有复杂水体的地震波传播模拟问题.
Käser和Dumbser(2006)最早将间断伽辽金法应用于二维地震波数值模拟中,并扩展到三维弹性波模拟问题(Dumbser and Käser,2006),黏弹性模拟问题(Käser et al.,2007),各向异性模拟问题(de la Puente et al.,2007)和变时间步长的模拟中(Dumbser et al.,2007b).随后,间断伽辽金法又被用于地震波震源动态破裂模拟问题(de la Puente et al.,2009; Pelties et al.,2012),孔弹性模拟问题(de la Puente et al.,2008; Boxberg et al.,2017; Zhan et al.,2018c; Shukla et al.,2019; Zhang et al.,2019)以及固液介质模拟问题(Käser and Dumbser,2008; Wilcox et al.,2010; Ye et al.,2016; Zhan et al.,2018a; Shukla et al.,2020).
间断伽辽金法中通量是非常重要的,目前间断伽辽金法中应用于地震波模拟问题中的数值通量主要有中心通量(Delcourte et al.,2009),Lax-Friedrich通量(廉西猛和张睿璇,2013; 张金波等,2018; 薛昭等,2014; 贺茜君等,2014,2021),Upwind通量(Käser and Dumbser,2006)和基于Rankine-Hugoniot跳跃条件的通量(RH-condition通量)(Wilcox et al.,2010)四种.Ye等(2016)在固体和液体内部采用中心通量,固-液边界基于中心通量增加额外的惩罚项实现固-液边界条件,但是中心通量会导致模拟的精度较低.Käser和Dumbser(2008)采用Upwind通量实现了复杂固-液介质地震波传播模拟.Wilcox等(2010)基于二维四边形和三维六面体网格在一阶速度-应变方程中采用RH-condition通量实现了固-液介质间断伽辽金地震波传播模拟.Zhan等(2018b)将该通量扩展到各向异性固-液介质的模拟中.
由于有限差分等其他数值模拟方法大部分都采用一阶速度-应力方程作为控制方程,开发基于速度-应力方程的间断伽辽金法更易于同这些数值方法联用实现混合数值模拟方法.此外,相比于三角形和四面体网格,四边形和六面体网格单元在复杂结构中应用时网格生成过程复杂.因此,本文针对二维三角形网格单元,发展了基于一阶速度-压力声波方程和一阶速度-应力弹性波方程、采用RH-condition通量的二维复杂固-液介质间断伽辽金地震波传播模拟算法,并通过一系列的数值模拟验证了模拟结果的准确性并分析了间断伽辽金法空间格式阶数与计算效率的关系.本文中使用的时间积分为低存储的4阶Runge-kutta格式(Carpenter 和Kennedy,1994).
1 原理
1.1 声波及弹性波方程
进行固-液介质地震波传播模拟时,液体介质用声波方程来表示,固体介质用弹性波方程来表示.一阶波动方程可以表示为
(1)
(1)对于声波方程:
(2)
其中,P表示压力,v表示质点振动的速度,ρ表示介质的密度,c表示波在介质中传播的速度.
(2)对于弹性波方程:

(3)
其中,τ表示应力,v表示质点振动的速度,ρ表示介质的密度,λ和μ是应力-应变关系中介质的拉梅常数.
1.2 节点间断伽辽金法
间断伽辽金法根据基函数可以分为模态和节点两种表示方式,他们之间可以互相转化.间断伽辽金法采用的是积分形式的方程来进行求解,其中又可以分为弱形式和强形式两种表示形式(Hesthaven and Warburton,2007),本文采用强形式方程的节点间断伽辽金法来进行求解,强形式方程的表达式为
=0.
(4)
其中,D表示一个网格单元,∂D表示网格单元的边界,上标k表示空间中第k个单元,表示拉格朗日插值多项式,其表达式为根据其性质可以建立Gauss-Legendre-Lobatto(GLL)点与基函数之间的关系(Hesthaven and Warburton,2007).u表示待求的波动方程中的变量,表示通量的部分,表示单元边界的外法线方向.
在进行求解时,如图1所示,先利用坐标变换将任意形状的三角形变换为等腰直角的标准参考三角形,其中Ψ表示任意三角形D与标准参考三角形I之间的映射关系.通过该变换每个单元的求解都可以统一起来.
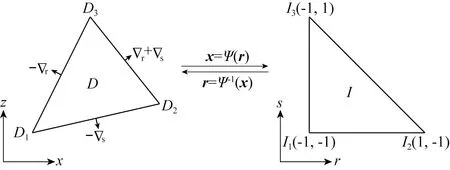
图1 任意三角形和标准三角形变换示意图
一个网格单元内的GLL 点分布和阶数有关.图2中N表示阶数,从图中可以看到,随着阶数的增加,一个三角形单元内的GLL点的个数也随之增加.其对应的基函数为
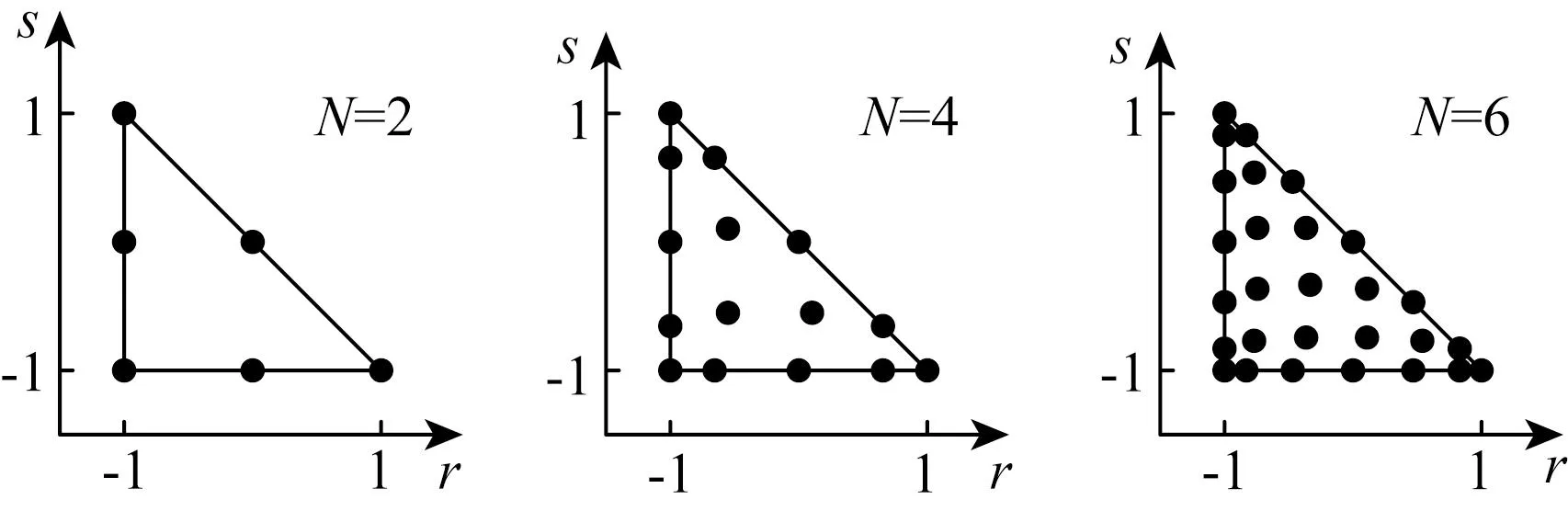
图2 不同阶数下GLL点在标准三角形中的分布

(5)

有限元法的基函数可以看作在整个计算空间内是连续的,在相邻单元的边界隐含了变量的连续性条件,间断伽辽金法的基函数只作用于单元内部,相邻单元之间采用通量来进行波场的传递.这样的方式使得每个单元都可以独立进行求解,因此易于并行处理.此外,对于固-液边界等非连续性边界,施加边界条件也更加灵活.
1.3 RH-condition通量
基于Rankine-Hugoniot跳跃条件推导的数值通量(RH-condition通量),考虑了相邻单元之间的波阻抗差异,更加符合物理规律.曹文忠(2022)通过一系列的数值模拟发现,在声波和弹性波介质中,存在强波阻抗差异时,只有RH-condition通量可以始终保持稳定,Upwind通量,Lax-Friedrich通量都会出现稳定性问题.
求解方程是在笛卡尔坐标系下来表示各个分量的,但是在进行通量计算时,使用单元边界法向分量的波场值.首先对变量进行坐标旋转得到对应的法向分量,计算出局部的通量后,再进行一次逆变换得到笛卡尔坐标下对应的通量值.定义单元边界的法线方向n=(nx,nz).
(1)声波方程坐标旋转:
(6)
其中,旋转矩阵T及其逆矩阵为
(7)
(2)弹性波方程坐标旋转:

(8)
其中,旋转矩阵T及其逆矩阵为
(9)
对于式(4)中的通量部分,其离散后的形式为
(10)
其中,Ne表示网格单元中边的个数.
根据声波方程中的连续性条件:
(11)
可以得到对应的通量(具体推导过程见附录):
(12)
其中,[[·]]符号表示单元边界两侧的波场差,例如[[a]]=a+-a-.类似地,弹性波方程的RH-condition通量为
(13)
式(12)和式(13)得到的是沿着单元边界外法线方向的通量,波动方程是在笛卡尔坐标系进行求解的,将其分别代入式(10),即可得到声波和弹性波在笛卡尔坐标系下的通量.
1.4 固-液边界条件
在固-液边界,如图3所示,固体介质中界面法向方向的正应力和液体介质中的压力的相反数存在连续关系,其法向的速度分量也存在连续关系.固体介质中的剪切应力在固-液边界处为0,其余分量没有约束.
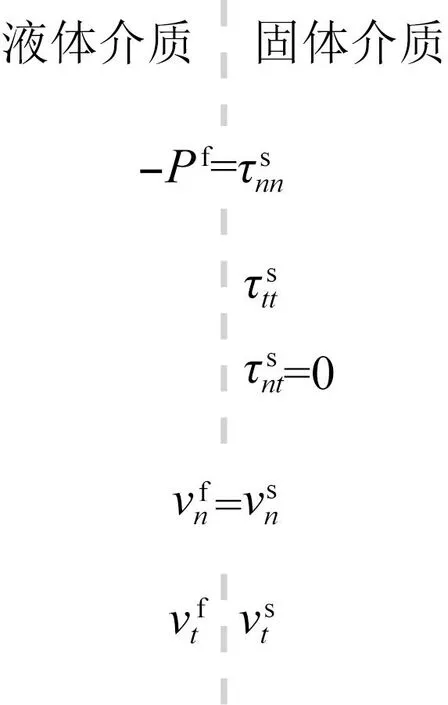
图3 固-液边界条件示意图
根据图3中固-液边界不同分量之间的关系,可以得到固-液边界条件为
(14)

(1)声波方程固-液边界通量处理:
(15)
(2)弹性波方程固-液边界通量处理:
(16)
实际计算时,在声波介质中的固-液界面,将式(15)代入式(12),在弹性波介质中的固-液界面,将式(16)代入式(13)即可实现固-液边界条件.
1.5 吸收边界条件
本文中使用吸收边界条件来对避免波场在边界位置的反射.吸收边界条件满足在边界位置流入的波场为0.
(1)声波方程吸收边界通量处理:
(17)
(2)弹性波方程吸收边界通量处理:
(18)
实际计算时,在计算区域的边界,将式(17)代入式(12),式(18)代入式(13)既可以实现吸收边界条件.
2 固-液介质模拟结果
本节中,首先采用水平层状固-液模型验证了模拟结果的准确性,并分析了不同网格单元大小与空间格式下模拟效率和模拟精度的关系.然后通过sin型起伏固-液模型进一步验证在复杂情况下的模拟结果的准确性.最后,对不规则形状固-液界面的模型进行模拟来说明本文提出的方法可以用于复杂固-液边界的地震波传播过程模拟问题.
2.1 水平层状模型
首先,使用水平层状固-液模型来验证模拟结果的准确性.图4展示了模型的大小,介质参数及震源和检波器的分布.震源位于固-液界面上方100 m处,检波器共有两组,分别位于固-液界面上下各1 m的位置.生成网格的平均边长约为70 m,最小的边长51 m,最大的边长99 m.震源时间函数是中心频率8 Hz的Ricker子波,震源类型为压力源.声波和弹性波介质参数参考了Komatitsch等(2000)文章中使用的介质参数.计算时采用5阶格式进行计算,时间步长为0.00085 s,并且使用谱元法作为参考解进行对比,谱元法采用边长40 m的正方形网格,4阶格式,时间步长为0.00085 s.图5展示了模拟的波形结果,可以看到本文提出的间断伽辽金法与参考解谱元法差异非常小,这说明施加的固-液边界条件是准确的.图6是模拟得到的波场快照,从图中也可以看到,在固-液界面位置,Vx分量存在不连续的现象,而Vz分量始终保持连续,这也与固-液边界的物理特征相符.

图4 水平层状固-液模型的介质参数,震源和检波器分布

图5 水平层状固-液模型波形对比
在间断伽辽金法中,单元的边界存在两组波场值,尤其是在低阶格式时,由于网格单元数量增加,会有大量的节点存在两组波场值,降低了计算效率.在本文中,单元网格大小是指单元的边长,由于采用的是三角形网格,在划分时难以生成大小一致的网格,因此本文中的单元大小指的是平均的网格边长.表1展示了在每波长网格点基本一致时的对比结果,其中在分析绝对误差最大值时使用的参考解为120 m单元大小10阶格式得到的波形.从中可以看到,1阶格式的计算时间为2阶格式的2.58倍,且绝对误差更大.4阶格式相比2阶格式计算精度更高,且计算时间更少.8阶格式计算精度最高,但计算量也有了明显的增加.在低阶格式时,由于存在大量重复的波场值导致计算量增大,导致计算时间增加.随着阶数的增加和网格单元边长的变大,重复的节点数大量的减少,使得计算量也显著减小.在计算空间偏导时,需要进行矩阵乘法的运算,随着阶数的继续增加,矩阵的规模会迅速增加,导致计算量增大,计算时间也随之增加.更高阶的格式理论上使用更少的每波长网格点即可达到低阶格式相同的误差,因此,这里的对比不够严格.不过在特别高阶格式时,为了提高计算效率网格单元会更大,但是对于一些复杂结构问题,网格划分时需要准确刻画复杂界面形状,网格单元边长不能过大,此时选取高阶格式会存在一定的问题.
通过上面的对比表明,选取合适的阶数才能更好的提高间断伽辽金法的计算效率.表2分析了在4阶格式下,不同网格单元大小时,绝对误差最大值与计算时间的关系,参考解与表1中的保持一致.可以看到,随着网格单元的变大,绝对误差也随之增加,计算时间与单元数成正比.通过分析可以看到,在4阶格式下,每波长5~6个格点时,与参考解的误差可以控制在1%左右.

表2 4阶格式不同单元大小下,节点数、计算时间域绝对误差最大值对比
2.2 sin型起伏模型
下面进一步对存在固-液界面起伏模型的模拟结果准确性进行验证,采用的是sin型起伏固-液模型.图7展示了sin型起伏界面模型的大小,介质参数及震源和检波器的分布.生成网格单元的最小边长为25 m,最大的边长为61 m,平均网格单元的边长约为40 m.选取空间4阶格式进行计算,时间步长为0.00085 s,震源参数与水平层状模型中的一致.参考解同样为谱元法模拟得到的波形记录,其网格单元边长为50 m,空间4阶格式进行计算.图8展示了模拟得到的波形记录,与水平层状固-液模型类似,本文提出的方法得到的结果和参考解的差异非常小,说明了该方法可以用于复杂固-液介质地震波传播过程模拟问题.
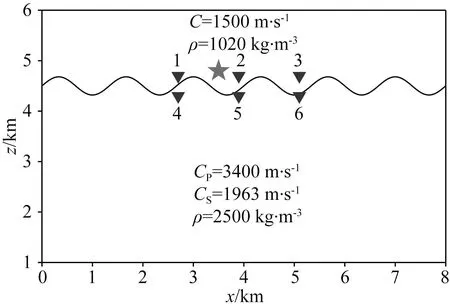
图7 sin型起伏固-液模型的介质参数,震源和检波器分布
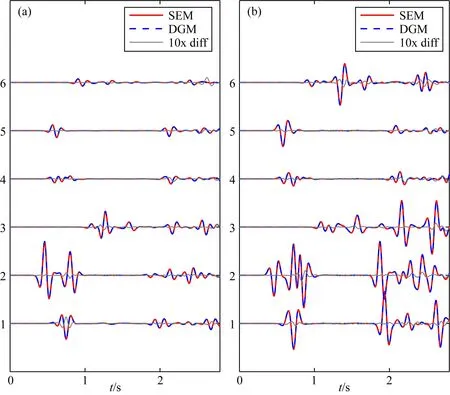
图8 sin型起伏固-液模型波形对比
2.3 复杂结构模型
通过前面的对比,说明本文提出的方法可以用于计算复杂固-液模型地震波传播模拟问题.图9展示了一个含有不规则复杂固-液边界的模型.有限差分类方法难以生成对应的结构化网格,传统的谱元法由于需要使用四边形网格单元,针对此类问题其网格生成不够灵活,基于三角形网格的间断伽辽金法可以灵活的处理此类复杂结构.图10展示了间断伽辽金法模拟得到的波场快照,从图中可以看到,在水平固-液界面位置处,Vx分量存在不连续现象,Vz分量保持连续.在竖直固-液界面位置处,Vx分量保持连续,Vz分量存在不连续现象,这与物理规律相符,也说明了本文提出的间断伽辽金法可以在复杂结构时准确的施加对应的固-液边界条件,能够模拟复杂固-液介质下的地震波传播.

图9 复杂固-液模型的介质参数,震源和检波器分布

图10 复杂固-液模型波场快照(第一列对应Vx分量,第二列对应Vz分量)
3 结论
本文基于Rankine-Hugoniot跳跃条件得到的RH-condition通量发展了复杂二维固-液介质间断伽辽金地震波传播模拟算法,该数值通量考虑了单元两侧的波阻抗的差异,更符合物理规律.使用该算法模拟了水平层状固-液模型和sin型起伏固-液模型波形记录,并与谱元法模拟结果进行对比验证了该方法的准确性.通过复杂模型波场快照说明该方法在复杂模型时依然可以准确的施加固-液边界条件,能够对复杂固-液模型地震波传播过程进行准确模拟.在水平层状固-液模型中通过一系列的数值实验表明,低阶格式计算效率和精度都较低.在高阶格式时,相同精度条件下,网格单元的边长更大,但是过大的网格边长在网格划分时不能准确刻画出复杂界面的形状,这会导致模拟结果出现一定的误差.因此在实际模拟时,应该根据实际问题来选择阶数和网格单元边长,但建议避免采用低阶格式来进行计算.
附录A RH-condition通量推导过程
Rankine-Hugoniot跳跃条件是计算通量的一种方法(Toro,1997).目前也越来越多的应用于地震波数值模拟问题中(Wilcox et al.,2010; Zhan et al.,2017,2018b; Duru et al.,2022; 曹文忠,2022).曹文忠(2022)给出了该通量在一阶速度-压力声波方程和一阶速度-应力弹性波方程中的详细介绍及推导过程,本文以声波方程为例进行简单的介绍.如附图1所示,横轴中0的表示相邻单元的边界,其两侧分别对应不同的单元,其介质参数和所需求解的波场值分别用上标“-”和“+”来表示,上标“*”表示加上通量后的波场值.

附图1 二维声波RH-condition示意图
本文在计算通量时,将x方向旋转到法向方向,将公式(2)中矩阵A进行特征值和特征向量分解可以得到:
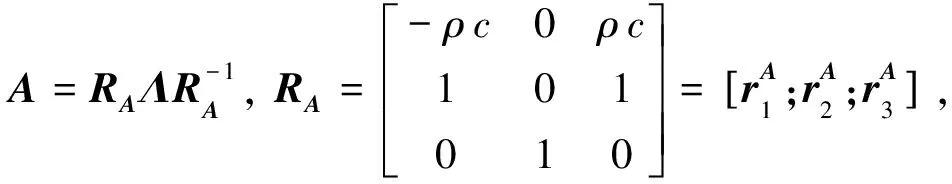
(A1)
根据Rankine-Hugoniot跳跃条件可以得到:
(A2)

(A3)

(A4)
根据声波方程中的连续性条件:
(A5)
根据上式关系,通过求解2元1次方程组可以得到:
(A6)
其中,[[·]]符号表示单元边界两侧的波场差,例如[[a]]=a+-a-.将式(A6)代入式(10)和(12)即可得到声波方程的通量.同样地,可以很容易得到弹性波方程中:
(A7)
将公式(A7)代入公式(10)和(13)即可得到弹性波方程的通量.
