全并联AT牵引供电系统雷击故障测距多路径行波算法研究
2024-02-04钟汉华陈剑云傅钦翠
钟汉华,陈剑云,华 敏,傅钦翠,石 杰,夏 天
(1.华东交通大学 省部共建轨道交通基础设施性能监测与保障国家重点实验室,江西 南昌 330013;2.中车戚墅堰机车有限公司 工艺技术部,江苏 常州 213011)
全并联AT供电方式是牵引供电系统中特殊的一种供电方式,并广泛应用于高速铁路中[1]。快速、精确的故障定位对恢复铁路运营具有重要意义。故障测距方法根据其原理可以分为阻抗法、行波法和人工智能法。行波法具有不受故障类型、过渡电阻、线路系统结构变化的影响等优势[2],适用于高速铁路故障测距。
然而,由于AT牵引供电系统结构复杂,其线路不对称,行波传播特性难以分析,导致行波法应用于全并联AT牵引供电系统故障测距精度不高。关于全并联AT特殊结构对行波传播特性的影响这一主题,已有学者进行了研究。傅钦翠等[1]将行波分解为同向和反向模量,得出了同向模量经过AT后波尾衰减过快以及反向模量只在故障区段内折反射的结论。熊列彬等[3]研究了行波传播至牵引变电所和线路末端时,由于牵引网中AT变压器通过并联横联线并接上下行,存在行波通过并联结构窜入上行或者下行线路的现象。此外,AT处的并联结构会使行波发生折反射[4],使得行波传播路径难以分析。同时,牵引网线路的参数频变特性[5-6]以及行波在牵引网上传播的色散现象[7]导致行波传播波速难以确定。
由上述分析可知,全并联AT牵引网雷击故障测距存在以上行波路径难以有效识别、波速难以确定的问题。
基于此,本文提出一种基于多路径行波且消去波速的测距方法。通过分析全并联AT牵引网结构对行波传播特性的影响,总结出行波经过牵引变电所、AT、线路末端时的传播路径幅值、极性的变化规律,最后基于多路径上下行电流、电压行波极性分析,筛选出用于故障测距的多路径行波,推导出消去波速的测距方程。
1 AT牵引网雷击故障仿真与特性分析
为实现牵引网雷击故障行波性质的有效识别,研究了雷击故障后,全并联AT牵引网特殊结构对行波传播的影响。
1.1 全并联AT牵引网结构
全并联AT牵引供电系统具有供电距离长、传输功率大的特点,目前已普遍应用于重载高速列车专线上[8]。全并联AT牵引供电系统见图1。牵引变压器的二次侧端子分别接入接触网和正馈线,二次侧线圈中性点接钢轨[9]。每隔8~12 km,将自耦变压器并入接触网和正馈线间。在自耦变压器、牵引变电所、分区所处通过横连线将上下行线路并联连接,从而实现上下行并联运行[10]。
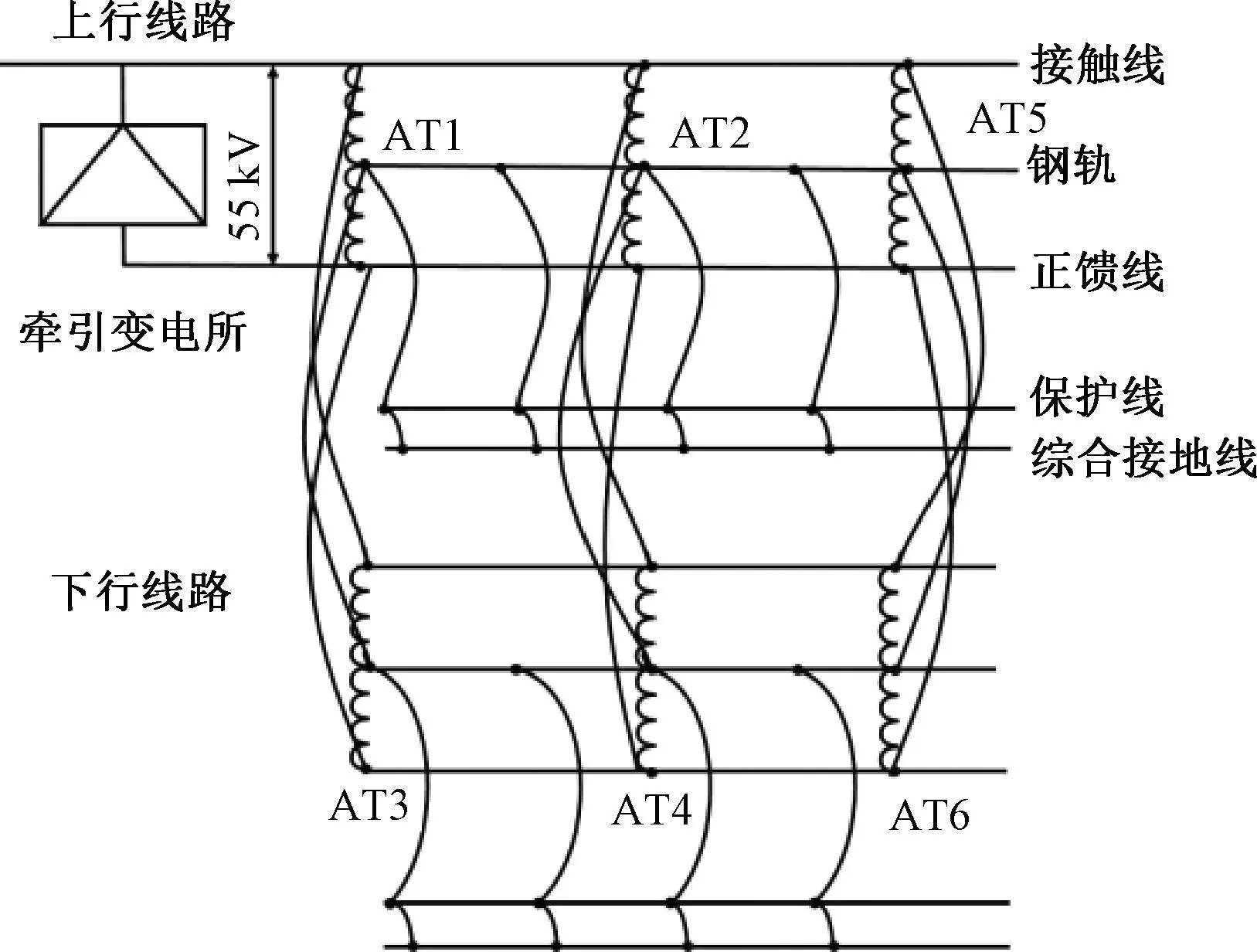
图1 全并联AT牵引供电系统
全并联AT牵引网由上下行承力索MW、接触线CW、正馈线PF、保护线PW、综合接地线CWG和钢轨R构成[11]。接触导线和承力索建模为一根二分裂导线;同时左右两根钢轨也建模为一根二分裂导线,合并分裂导线并消去地线后,全并联AT牵引网等效为六相等值相导线[12],全并联AT牵引供电系统截面见图2。
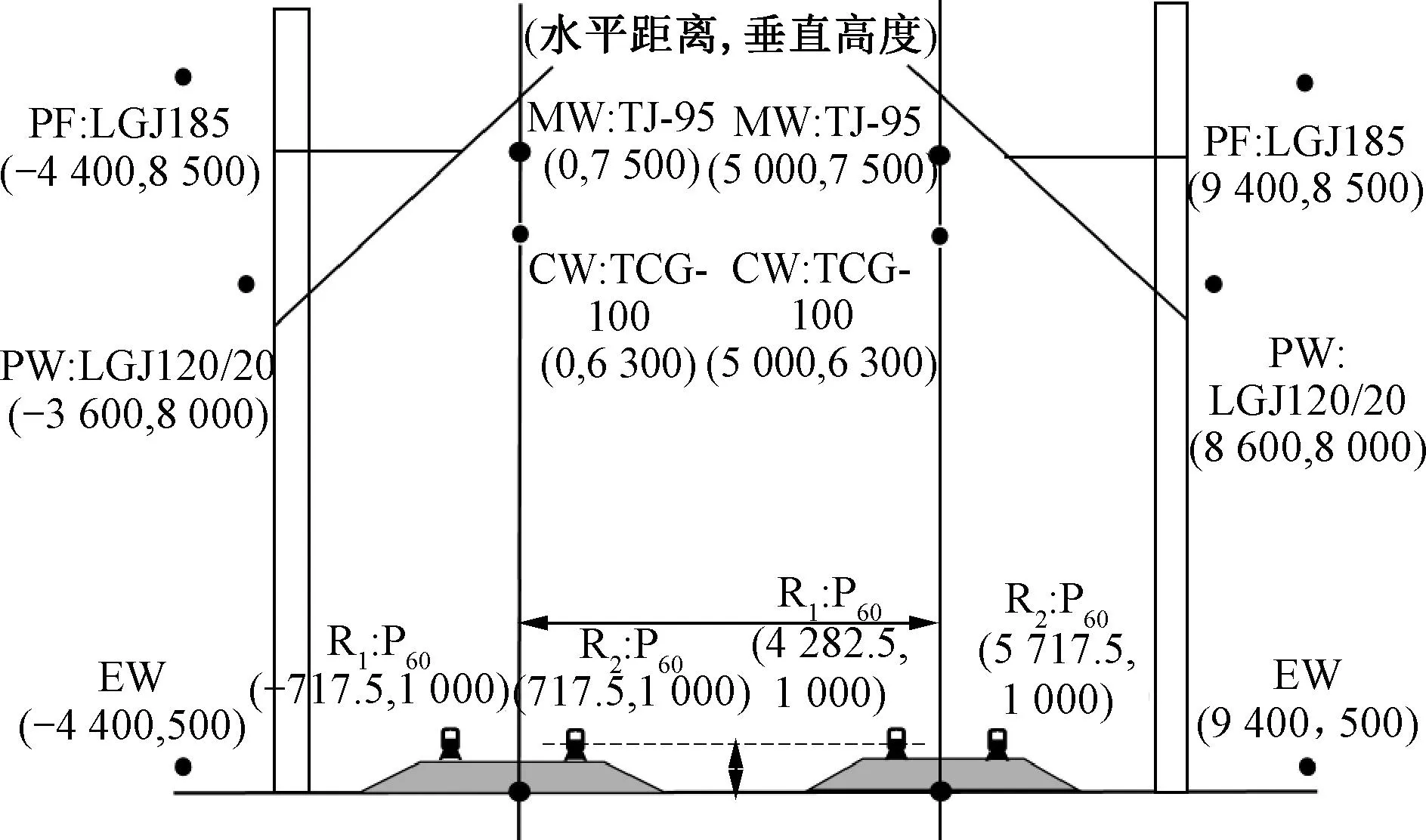
图2 全并联AT牵引供电系统截面(单位:mm)
1.2 雷电暂态信号仿真
采用EMTP完成全并联AT牵引供电系统雷击故障建模并进行雷电暂态信号仿真。全并联AT牵引供电系统雷击故障建模见图3。
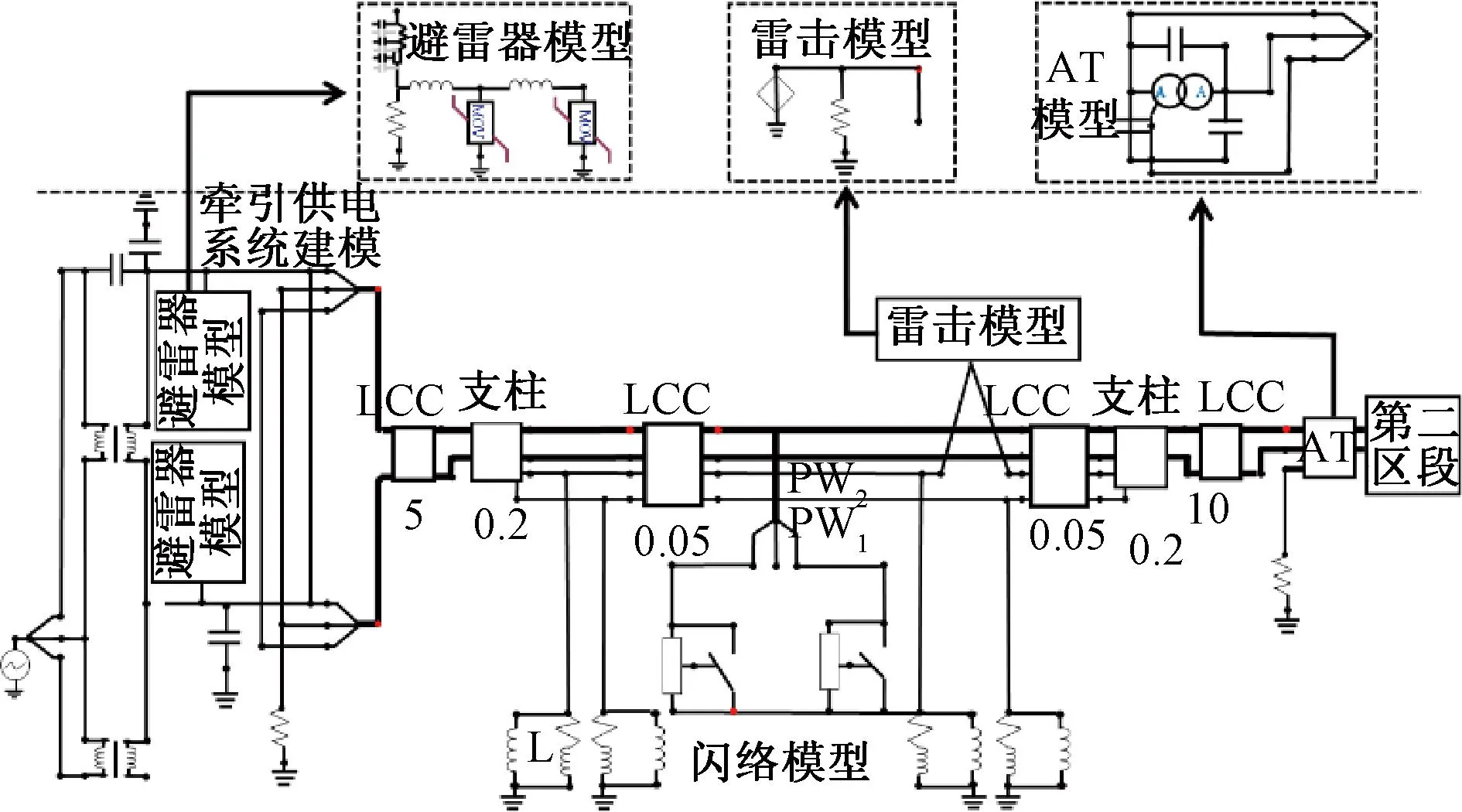
图3 全并联AT牵引网雷击故障建模示意(单位:km)
1)牵引线路建模
牵引线路采用LCC元件进行建模,复线AT牵引线路用6相JMarti线路模型来描述,其导线参数见表1。

表1 牵引网导线参数
2)自耦变压器建模
雷击过电压计算中,需要考虑波在变压器绕组中的传递,因此在绕组间跨接适当电容。文献[13]分析了几种变压器的高频模型,得出了π电容+BCTRAN的模型更为准确,可精确模拟高频下的变压器。
本文考虑电容特性的自耦变压器暂态模型BCTRAN采用回路阻抗矩阵来描述,将变压器各绕组视为一组相互耦合的电感,构建变压器的等值电路见图4。
图4中,P、S分别为高压、中压绕组端子;N为公共端。π电容C1、C2、C12采用EMTP推荐的典型值0.005、0.01、0.01 μF[1]。仿真中AT容量取10 MV·A,自耦变压器性能参数[14]见表2。

表2 自耦变压器性能参数
3)变压器建模
本文采用V/x接线牵引变压器,利用单相双绕组变压器SAT模型进行仿真实现。变电所牵引变压器额定数据见表3。
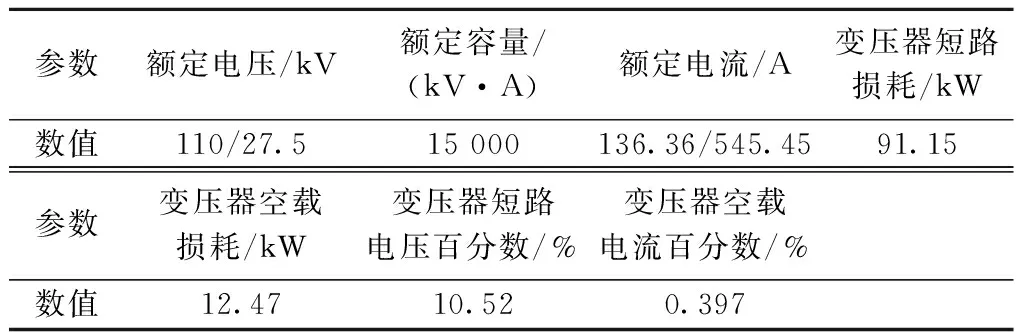
表3 变压器额定数据
4)避雷器建模
避雷器模型采用Pinceti等[15]建立的IEEE简化模型。高速铁路供电系统避雷器参数见表4[16]。

表4 避雷器参数
5)雷电源模型
(1)
式中:I0为雷电流幅值;ε为幅值修正系数;α、β为波前和波尾衰减系数。
建模时,雷电波模型采用Heidler冲击波电源,设置波头时间为2.6×10-6μs,半波时间为5×10-5μs[17-18]。
1.3 雷电故障行波传播过程
全并联AT牵引网线路发生雷击故障后,行波传播至牵引变电所、线路末端和AT,通过并联横联线会向相对的上下行线路进行透射,同时在AT处会产生反射与折射。
以牵引变电所作为量测端,故障电流分布见图5,雷击电流从故障点向两端传播,经过牵引变电所、AT所、分区所时会产生折反射并通过横联线窜入上下行线路。此种情况会导致行波传播过程复杂,行波性质难以有效识别。
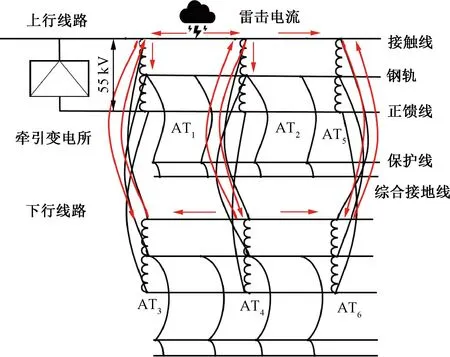
图5 全并联AT牵引供电系统雷击电流分布
结合行波折反射系数计算公式,分析行波经过AT所、牵引变电所、末端后行波的折反射规律。
节点连接多条线路的电流、电压行波折反射系数为[19]
(2)
(3)
(4)
式中:n为节点连接线路的数目;βu、βi为电压、电流行波的反射系数;αu、αi为电压、电流行波的折射系数。
1)牵引变电所、线路末端相当于开路,上下行并接,用n=2来表示此节点。
DEA模型涉及到投入——产出指标体系,只有科学构建指标体系,才能更加准确的测度效率变动。本文在前人指标体系构建的基础上,投入指标选取农林牧渔业产业城镇单位就业人员、农林牧渔业总产值、农林牧渔业全社会固定资产投资额,衡量各要素投入状况,产出指标选择工业产业增加值、农村居民人均可支配收入,衡量要素产出状况。
经过式( 2 )~式( 4 )计算可得
βu=-βi≈0
(5)
αu=αi≈1
(6)
从式( 5 )和式( 6 )可知,行波经过牵引变电所和线路末端时,会有较小的反射波[3],大部分经过并联横联线透射至相对的上下行线路上。

可以看出,计算后电压、电流反射行波幅值变为原来的一半;透射至相对的线路以及折射至另一区段的电压、电流行波幅值约为1/6、1/2。
3)雷电波在短路点的反射波受过渡电阻影响,大多数实际故障情况下,过渡电阻幅值相对较小,雷电波反射波幅值相对来说较大、折射波幅值较小[20]。
1.4 牵引网线路相模变换
全并联AT牵引网上下行并联,上下行以及相间存在耦合,进行分析时,需要对其进行解耦计算[11]。行波频率范围广,当频率大于工频时,可以认为相模变换矩阵与频率无关[21],采用5 kHz下经过实数化的电流相模变换矩阵Ti[1]为

1.5 雷电故障行波极性分析
电压、电流行波经过牵引变电所、线路末端以及AT所时,不仅会发生折反射,其极性也会产生变化,因此不同路径的行波,其电压电流极性存在差异,可以为故障定位提供依据。
假设故障发生在第一区段上行线路:初始电流行波为故障点向牵引变电所传播的行波(假设方向为负,电荷为负,以--表示),故障点向反方向(AT)传播的电流行波(方向为正,电荷为负,+-);初始电压行波(假设电荷为正,极性与方向无关,+),初始电压波电流波幅值以1来表示。左行波表示故障点朝向TS(左方向)的初始行波;右行波表示故障点朝向末端(右方向)的初始行波。
雷击故障行波传播经过AT、牵引变电所、线路末端,其幅值和极性变化结果见表5。
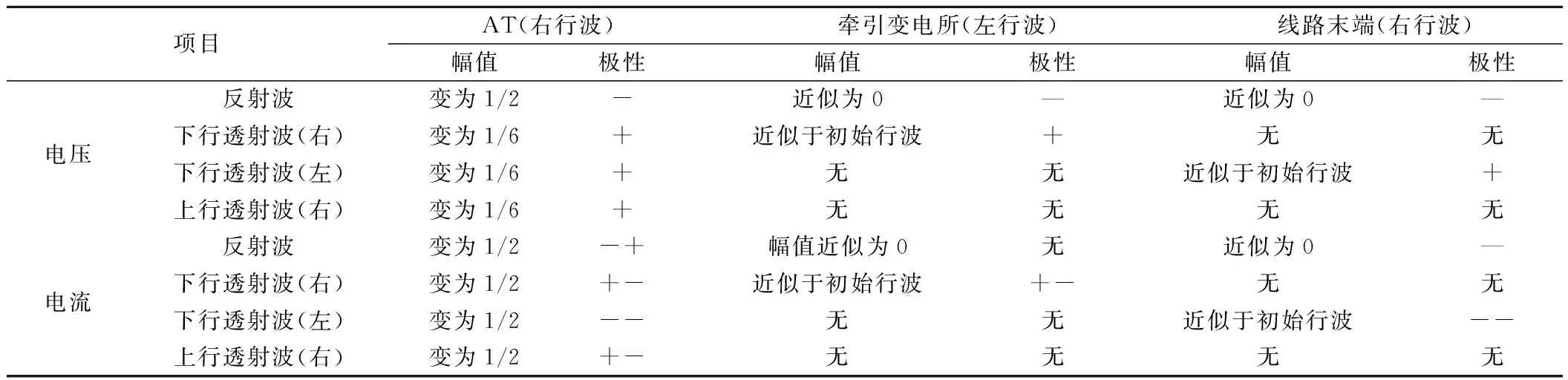
表5 雷击故障行波传播特性
1.6 雷击故障行波传播路径分析
本文需要筛选特定路径的行波进行测距,依照上节结论,给出雷击故障下,前5个有效行波路径的故障距离和上下行电流、电压行波极性。假设电流行波向右传播为正方向,初始行波极性为负;电压行波极性和方向无关,初始极性为正,以牵引变电所(TS)作为观测点,第一、二区段各行波传播路径见表6、表7。

表6 第一区段各行波传播路径

表7 第二区段各行波传播路径
由表6可知:
1) 2-B行波路径包含故障点的折射波,幅值较小,因此B路径可忽略。
2) 3-A路径包含一次AT反射,3-B路径包含一次AT透射以及一次故障点反射,波头奇异性、幅值均小于A路径,因此量测端观测波以3-A路径行波为基准。
3) 5′号电流、电压行波,故障点越靠近AT,其故障点反射波和AT反射波就越多,会形成震荡波形,其电流行波性质在观测点为+-,电压行波体现为+极性。
4) 6号电压、电流行波,牵引变电所以及线路末端反射波构成的行波路径,波形平缓,很难检测其奇异性,因此可忽略此路径行波[3]。
由表7可知,2′号电流、电压行波,故障点越靠近AT,其故障点反射波和AT反射波就越多,会形成震荡波形,其电流行波性质在观测点为--,电压行波性质为+。
2 AT牵引网雷击故障算法分析
2.1 故障区段确定
从机理上看,当故障发生在第一区段上行线路时,初始行波传播至牵引变电所端,上行量测端接收的行波极性为--,下行量测端接收的行波极性为+-,因此上下行电流行波为波形趋势相反的波形,见图6、图7。

图6 第一区段3 km上下行电流行波

图7 第一区段12 km上下行电流行波
从第二区段来看,当故障发生后,故障行波会通过中间AT所的并联横联线向上下行流动。因此,在牵引变电所上下行量测端的行波趋势基本一致,其波形见图8。

图8 第二区段18 km上下行电流行波
采用“相似度”来描述波形之间的相似程度,以达到区分故障区段的目的[23]。对任意两个上、下行电流向量A、B之间的余弦相似度可以表示为[24]
(7)
本文关注波形形状的相似程度,因此运算时取绝对值。两区段相似度计算结果见表8。

表8 不同区段相似度计算结果
2.2 第一区段故障测距原理
当故障发生在第一区段,从上述章节定义的行波路径1、2、3、4、5、5′,选取1、2、3路径行波进行测距,理论如下。
假设故障发生时刻t0,故障距离为x,第一区段长度为l1。
(8)
(9)
(10)
式中:t1、t2、t3分别为1、2、3行波波头的波到时刻。计算波到时刻的差值,可得
(11)
(12)
将式(11)和式(12)联立,故障距离x为
(13)
由式(13)可知,多路径行波算法推导所得故障测距公式可不考虑波速进行计算。推导出了第一区段测距所需的多路径行波之后,需要通过极性判据对其筛选。第一区段多路径行波极性判据见表9。

表9 第一区段多路径行波极性判据
结合表6,将故障距离归纳为
(14)
由式(14)可知,从时间序列上看,1、2路径行波为排序1、2的行波。由表9可得,从极性上判断第一个011和101即为1、2路径行波,极性为010的即为3路径行波。
经分析可知,当故障点向AT2移动时,故障距离x慢慢变大,当x=l1/2时,3、5路径行波时序相同,其路径重叠。由行波路径分析可知,3路径行波仅经过一次折反射,5路径行波经过两次折反射,其能量有部分经过折射减少,因此3行波的奇异性更强,重叠波电流电压极性以3路径行波为主,重叠波极性体现为010。第一区段3、5路径电压、电流重叠行波见图9、图10。
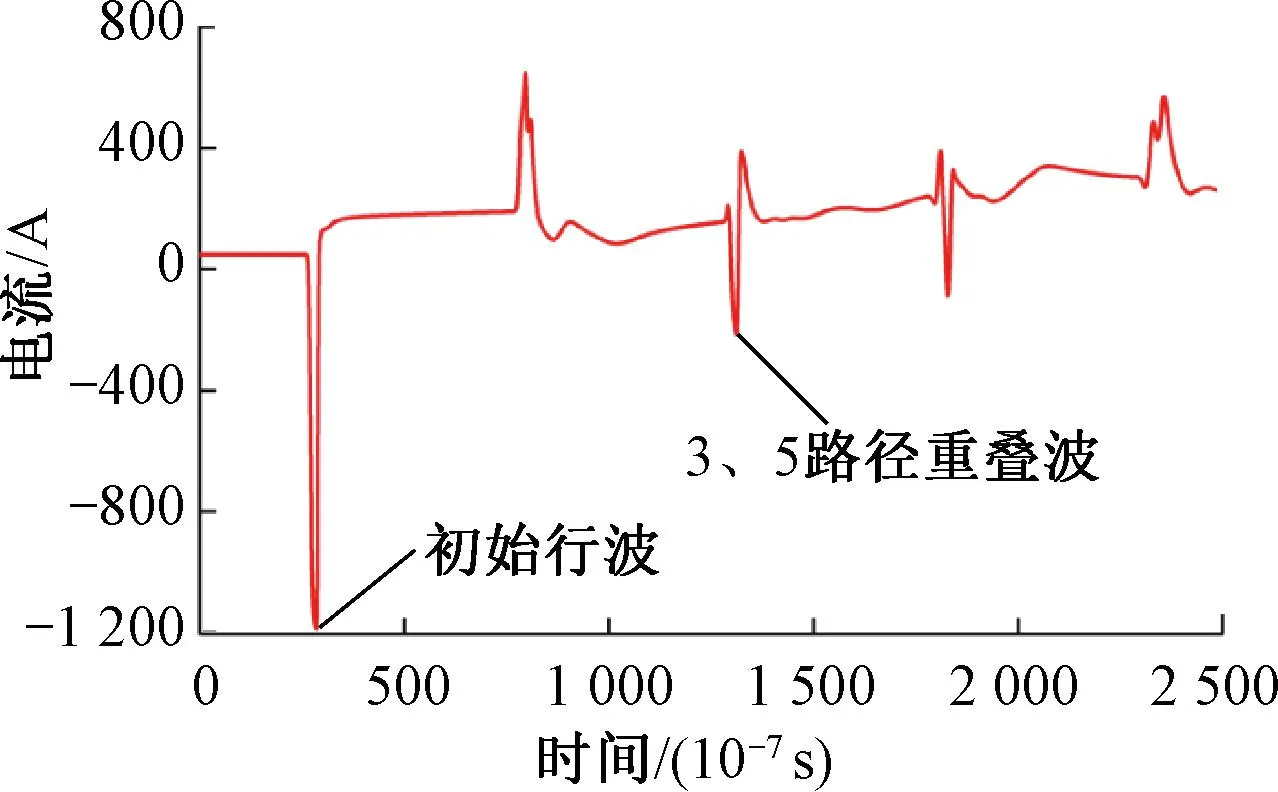
图9 第一区段3、5路径电流重叠行波
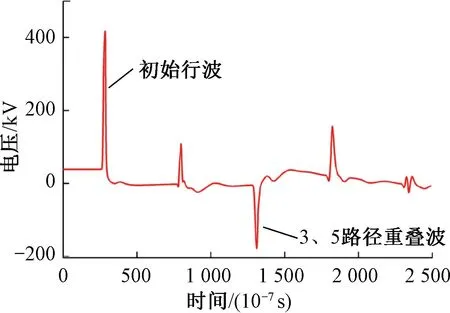
图10 第一区段3、5路径电压重叠行波
为验证上述分析,将重叠后的行波进行小波包变换进行分析,得出结果见图11、图12。小波包变换结综上所述,从极性上判断第一个011和101即为1、2路径行波,极性为010的即为3路径行波。

图11 重叠电流行波模极大值曲线

图12 重叠电压行波模极大值曲线
2.3 第二区段故障测距原理
当故障发生在第二个区段,从上述章节定义的行波路径1、2、2′、3、4、5。选取1、3、5路径行波进行测距计算,理论如下。
假设故障发生时刻t0,故障距离为x,第一区段长度为l1,第二区段长度为l2。
(15)
(16)
(17)
式中:t1、t2、t3分别为1、3、4路径行波波到时刻。计算波到时刻的差值,可得
(18)
(19)
将式(18)和式(19)联立,故障距离为
(20)
由式(20)可知,多路径行波算法推导所得故障测距公式可以不考虑波速进行计算。推导出第二区段测距所需的多路径行波之后,可以通过极性判据对其筛选。第二区段多路径行波极性判据见表10。
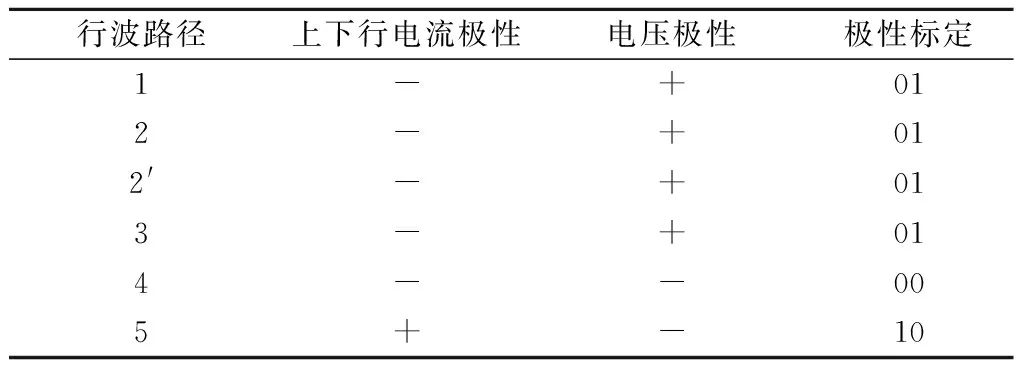
表10 第二区段多路径行波极性判据
结合表7,将故障距离归纳为
(21)
为识别1、3、5路径行波,仍存在3个识别问题需要进行分析。
2.3.1 2、3路径行波识别
由表10可知,第一个极性为01的行波即为初始行波。2、3路径行波极性均为01,且由式(21)可知,2、3路径行波随故障距离改变,其波到顺序也会发生改变,因此需要对其进行识别。以第二区段2、11 km的2、3电压行波路径为例进行分析,其波形见图13、图14。

图13 第二区段2 km 2、3路径电压行波
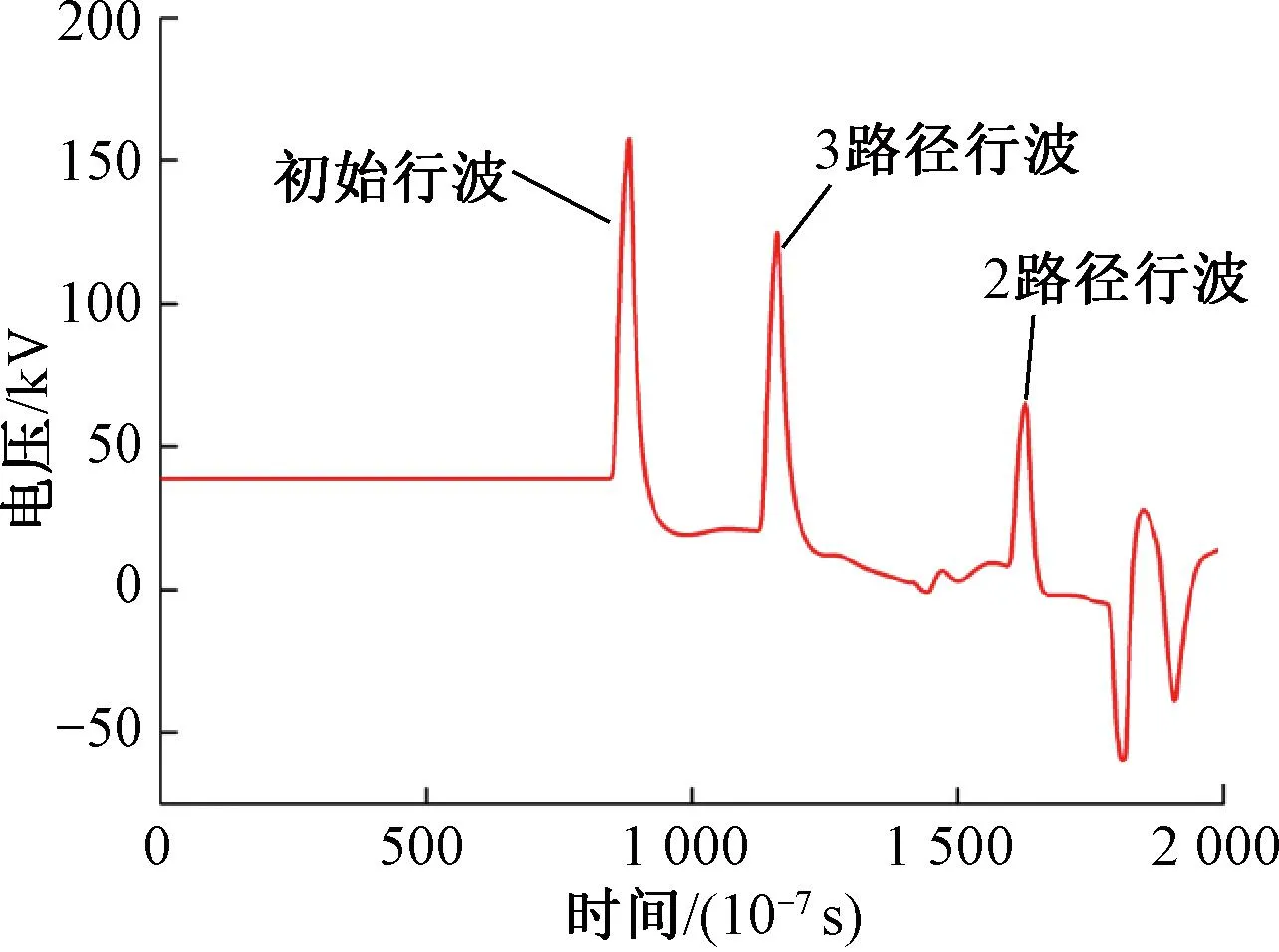
图14 第二区段11 km 2、3路径电压行波
由1.4节中行波路径分析可知,2路径行波经过两次反射一次透射,3路径行波仅经过一次透射,则3路径行波奇异性更强,采用小波包进行分析,结果见图15、图16。
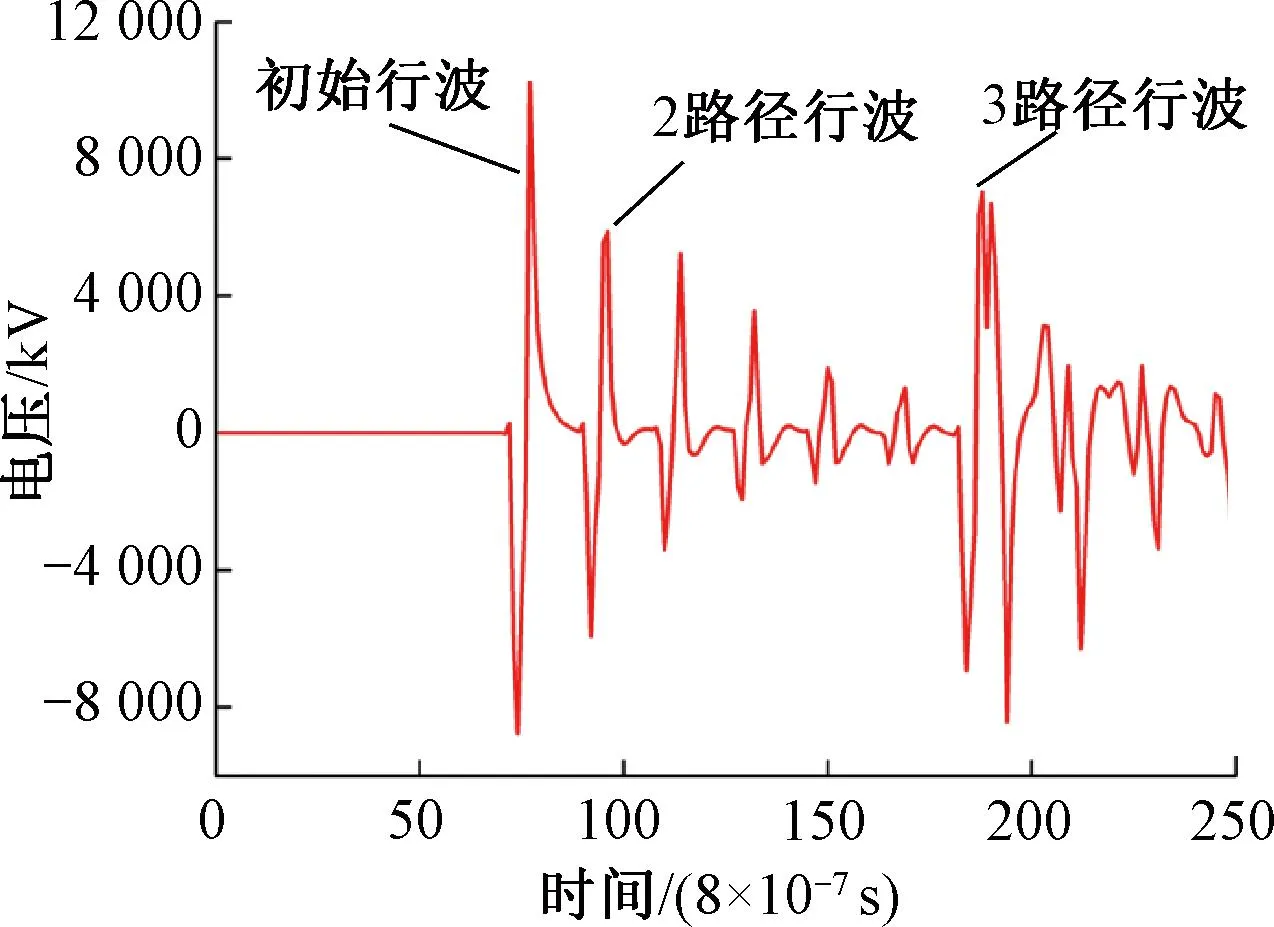
图15 第二区段2 km 2、3路径电压行波模极大值曲线
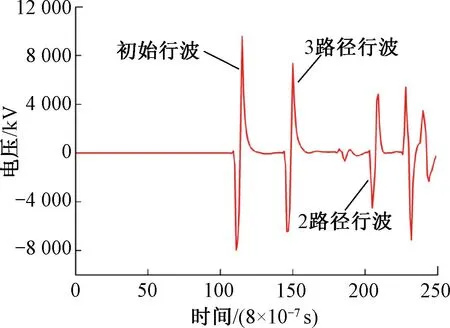
图16 第二区段11 km 2、3路径电压行波模极大值曲线
从图15、图16可以看出,3路径行波的电压模极大值比2路径行波大,可以依靠此规律对2、3路径行波进行识别。
结合式(21)和表10可知,当故障点向线路末端移动(x逐渐增大),3路径行波会发生移动,慢慢向1路径行波靠近,此过程中,会与2路径行波产生重叠。随后,其电压模极大值重叠达到最大,此时电压极性最强的脉冲即为3路径行波电压波脉冲。
因此,极性为01的路径行波即为初始行波,除去第一个极性为01的路径行波,且电压行波奇异性最强行波路径即为3路径行波。
2.3.2 4、5路径行波识别
由式(21)可知,当l1、l2距离不同时,4、5路径行波出现的位置不同,依照表10即可对4、5路径行波进行识别。当l1=l2时,4、5路径行波重叠。重叠波与未重叠波见图17~图20。

图17 4、5电压路径重叠行波

图18 4、5电压路径未重叠行波
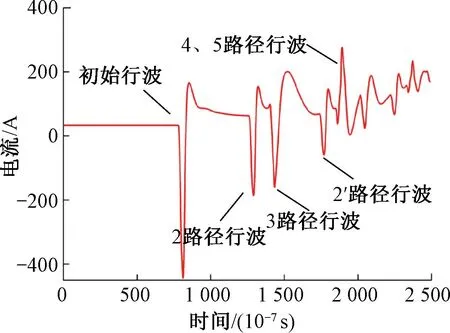
图19 4、5电流路径重叠行波
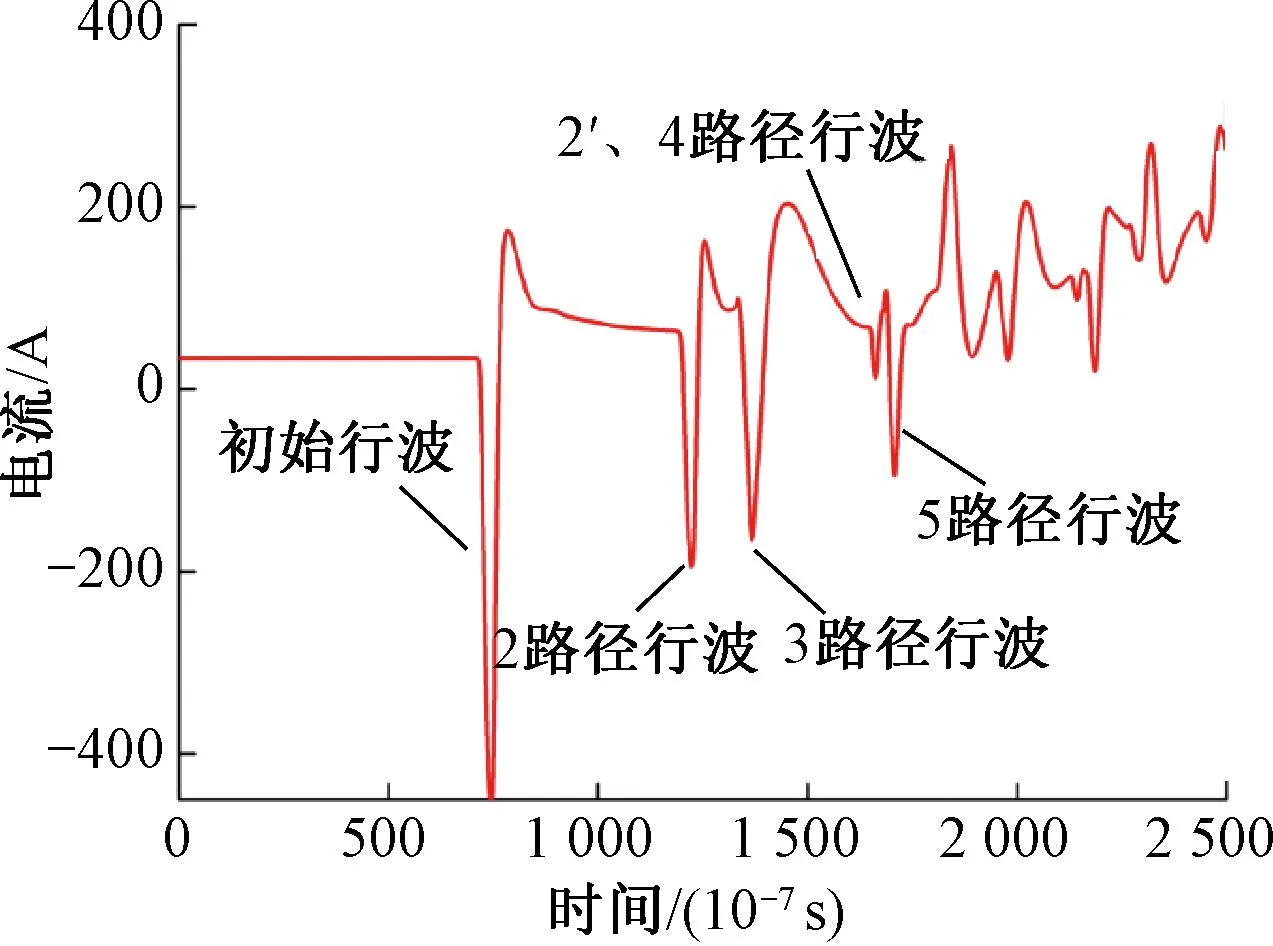
图20 4、5电流路径未重叠行波
对4、5路径行波重叠进行小波包变换,结果见图21、图22。

图21 4、5电压路径重叠行波模极大值曲线

图22 4、5电流路径重叠行波模极大值曲线
从图21、图22中可以看出,4、5路径行波重叠波电压极性为-、电流极性为+,极性标定为01,与5行波路径极性一致。因此不管第一区段和第二区段长度多少,极性标定为01的行波即为5路径行波。
2.3.3 3、4路径重叠行波极性强弱判定
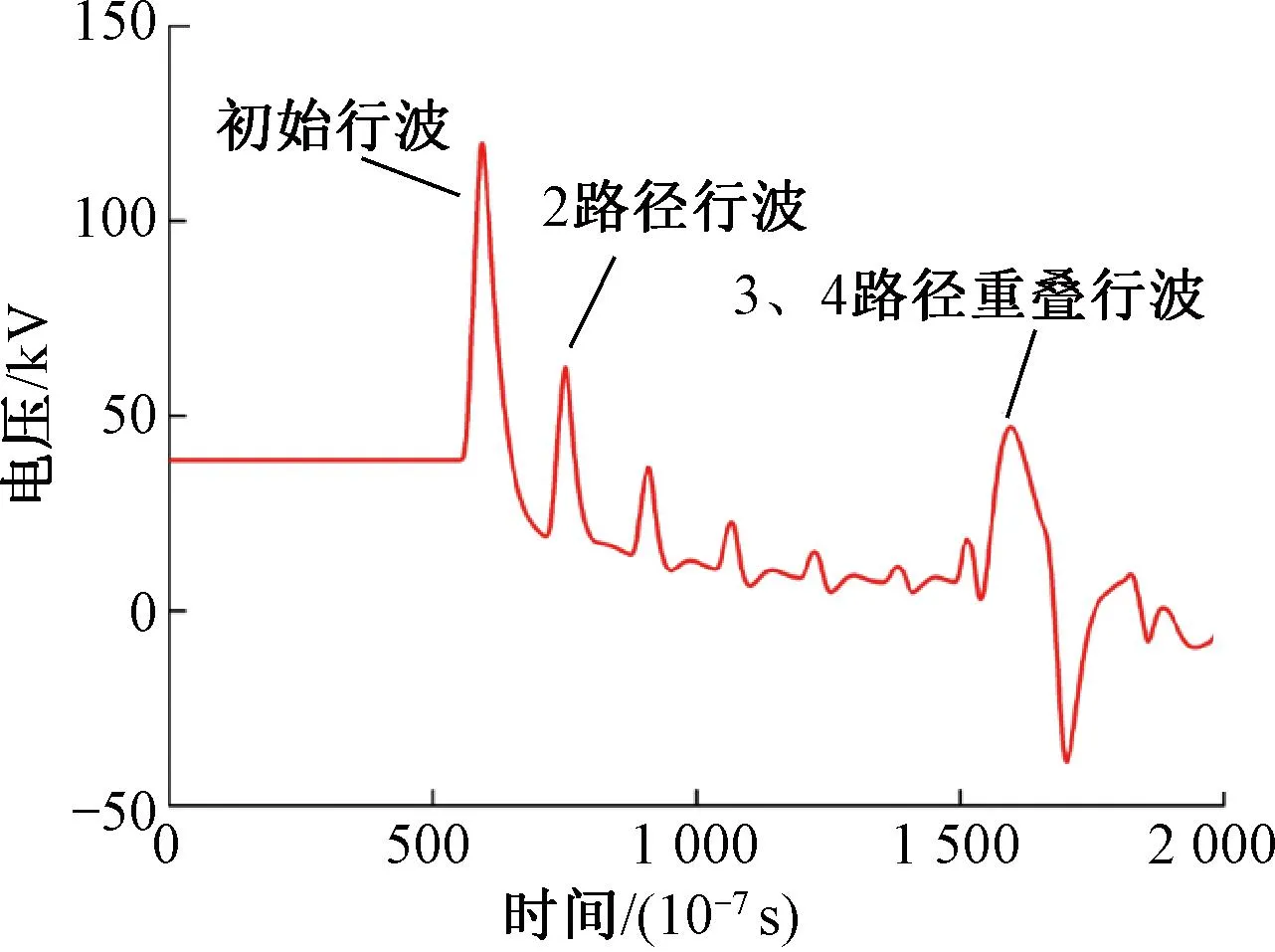
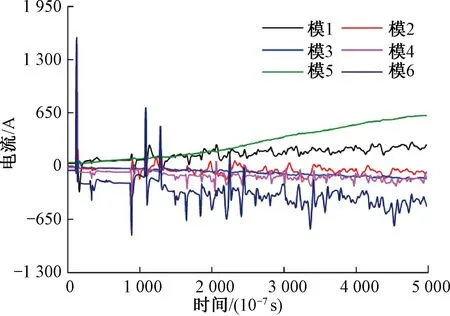
由式(21)可得,当l1 图23 3、4电压行波未重叠 图24 3、4电压行波重叠 3、4路径电流、电压行波重叠小波模极大值曲线见图25。 图25 3、4电压重叠行波小波变换结果 从图25可知,当3、4路径电压行波重叠以后,重叠波电压极性仍为+极性,且奇异性比2路径电压行波更大,电流极性相同,相互叠加。因此重叠后的电压极性为正,电流极性为正。此情况下,依旧可以按照极性判据进行判断。 将多路径行波方法应用于全并联AT牵引网雷击故障测距中,具体故障定位步骤如下: Step1当牵引供电系统发生雷击故障,通过放置在牵引变电所的行波采集装置对上下行电流、电压信号进行采集。 Step2针对全并联AT牵引网结构进行分析,研究其结构对行波传播特性的影响,总结出行波传播经过阻抗不连续点时,其幅值、极性的变化规律。 Step3分析不同区段下发生故障后,上下行电流行波传播过程,利用波形相似度识别故障区段。 Step4故障发生第一区段,则采用式(13)计算出故障位置;故障发生第二区段,则采用式(20)计算故障距离。 全并联AT牵引网雷击故障测距流程见图26。 图26 全并联AT牵引网测距流程 以图3所示全并联AT牵引供电系统为例,验证所提出的基于多路径行波的全并联AT牵引网行波测距方法的可靠性。 在EMTP中分别对不同区段长度的供电系统以及对距离牵引变电所不同距离发生雷击故障情况进行仿真。在EMTP中建立区段为14、16 km长的全并联牵引网线路,采样率设置为10 MHz,雷击故障点设为距离牵引变电所2.8 km处。牵引变电所端故障电流波形以及相模变换后的模电流见图27、图28。 图27 牵引变电所各线电流 图28 模电流曲线 从图28中可以看出,模6电流分量极性最强,因此选择模6分量进行故障测距。采用电流模6以及电压模5分量进行小波模极大值分析,得到结果见图29、图30。 图29 模6电流分量小波变换模极大值 图30 模5电压分量小波变换模极大值 从图29、图30可知,前4个电流电压波头极性见表11。 表11 电流电压极性 依照2.2节分析,按照式(13)计算故障距离为2.910 6 km,误差为0.110 6 km。 按照流程图,分别对不同区段长度的供电系统以及对距离牵引变电所不同距离发生雷击故障情况进行仿真,故障测距结果见表12。 表12 故障测距结果 本文结合小波模极大值理论,提出一种基于多路径行波的全并联AT牵引网测距方法,可以有效对AT牵引供电系统进行雷击故障测距。首先基于上下行电流行波传播的差异性,利用电流相似度识别故障区段。其次,探讨全并联AT牵引网结构对行波传播特性的影响,并对电流、电压行波传播路径进行标定。最后,基于多路径电流、电压行波极性分析,筛选出用于故障测距的多路径行波,推导消去波速的测距方程。 主要结论如下: 1)对不同区段的故障行波进行分析,得到不同区段故障下,上下行行波传播路径存在差异性,可以利用电流相似度进行故障区段判别。 2)对全并联AT牵引网上下行线路进行解耦,在行波传播特性分析的基础上,对电流、电压极性进行研究,得到不同路径下,上下行电压、电流行波的极性标定。 3)在上述分析基础上,提出基于多路径的行波方法,推导出消去波速的测距方程,测距结果不受牵引网区段长度、结构影响。当故障距离为8 km时,误差最小为33 m,当故障为25 km时,测距误差最大为191 m。该方法计算故障距离时,需要计算波到时刻,其误差取决于采样率和波到时刻的标定,采样率越高,则误差越小。本文采样率为Fs=10 MHz,波速按v=3×108m/s计算,算法理论误差在s=Fsv≈30 m之内。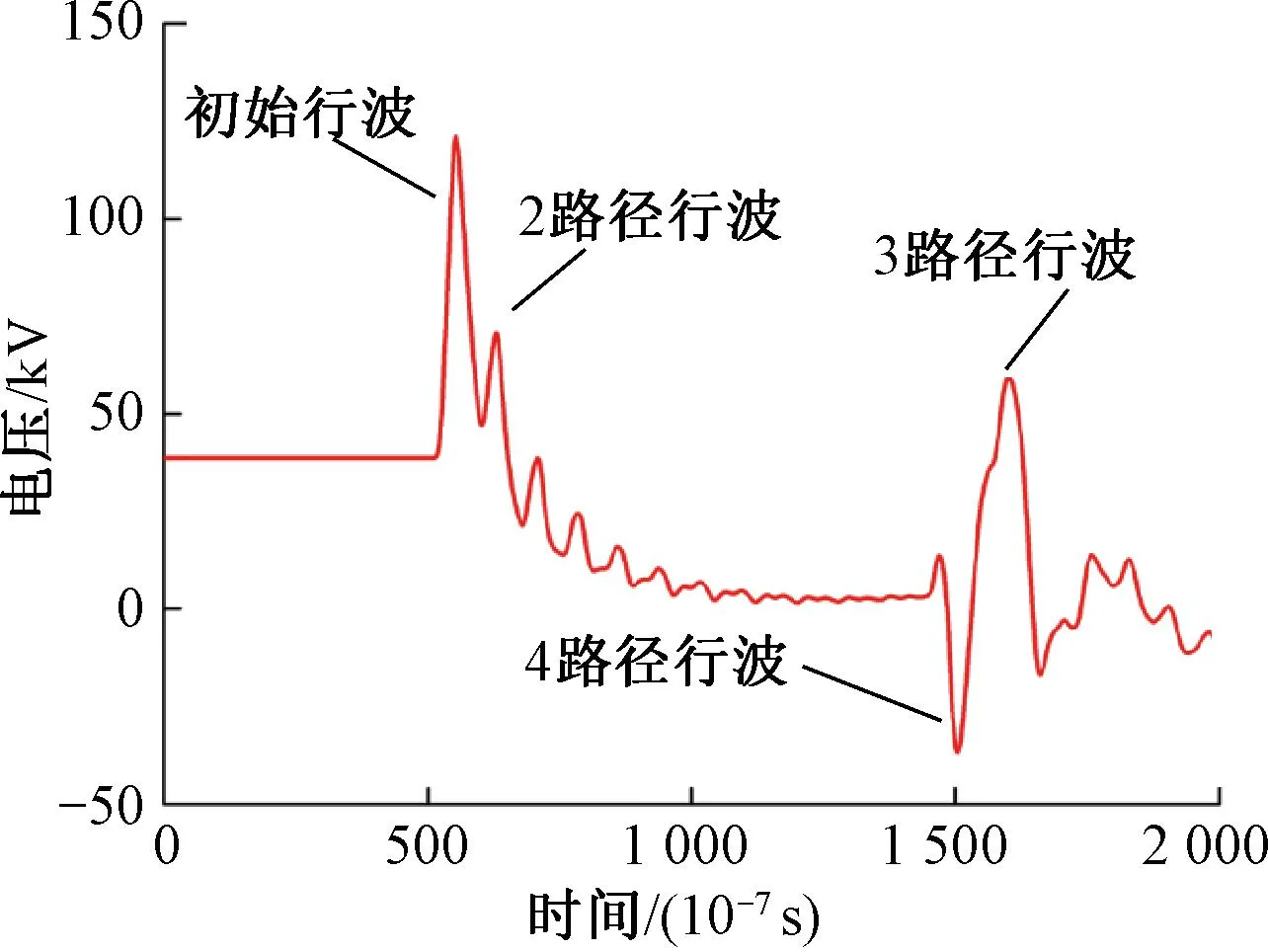

3 全并联AT牵引网雷击故障测距算法方案

4 算法验证





5 结论
