基于超声波换能器的钢筋机械损伤与锈蚀损伤检测及其对比研究

汪佳宇,陈铭刚,布占宇

（宁波大学 土木工程与地理环境学院,浙江 宁波 315211）

钢筋混凝土结构的整体性、可模具性、耐火性等均较好,在现代建筑领域应用广泛,但一直受其耐久性问题的困扰[1].为了减少经济损失、保障人身安全,有必要对钢筋混凝土结构中钢筋的损伤情况进行检测,了解内部钢筋是否损伤、损伤程度以及损伤位置,从而针对性地采取预防措施.

超声导波检测技术具有单点激励、检测耗时少且覆盖范围大、工作环境要求低等优点,已成为目前无损检测领域的研究热点之一[2-3].超声导波是平行于边界传播的弹性波,由波在介质中的不连续交界面间产生多次反射,进一步产生复杂的干涉和几何弥散形成.超声导波检测技术通过超声导波和构件的相互作用,由超声波换能器作为发射端,导波在构件内部传播后,对接收端换能器接收到的信号进行分析.若作为传播介质的构件本身存在损伤,从发射端发出的信号经过传播介质后声波参数会发生改变,如幅值衰减、模态变化及波速改变等,与未损伤时的信号对比,可以得出介质的损伤情况.

超声导波检测技术目前在土木工程领域应用广泛.Sharma 等[4-5]、Du 等[6]和雷鹰等[7]将超声导波技术应用在钢筋混凝土锈蚀检测中;Zheng 等[8]和Sriramadasu 等[9]通过数值模拟与试验结果对比,验证导波检测钢筋锈蚀的可行性;Liu 等[10]用超声导波检测钢筋在混凝土保护层厚度、水灰比以及不同种类钢筋条件下的锈蚀情况;Li 等[11]针对由锈蚀导致的钢筋混凝土界面剥离问题,对不同剥离长度的钢筋混凝土导波参数进行了研究;Sun 等[12]采用高阶纵向模态检测实心、蜂窝和空洞3 种不同钢筋混凝土界面的粘结条件;Lu 等[13]对钢筋混凝土梁进行4 点弯曲试验,将导波参数作为量化混凝土结构损伤指标;周琛等[14]提出了基于L(0,2)的超声导波检测方法,对损伤管道和焊接弯管进行识别与定位;徐阳等[15]对埋地管道缺陷检测进行了研究;张清华等[16]对钢桥面板足尺模型进行了试验,将超声导波用于检测纵肋对接焊缝疲劳裂纹.目前有关超声导波研究大都有关钢筋锈蚀和管道结构,对钢筋不同损伤的对比研究较少.

本文基于超声波换能器对钢筋损伤进行检测,从机械损伤和锈蚀损伤两方面入手,建立了损伤与超声导波特征的对应关系,并基于小波变换的时频分析方法判断钢筋的不同损伤状况.

1 理论分析

1.1 纵向模态

实心圆柱杆中存在3 种超声导波模态,即纵向模态、扭转模态和弯曲模态.其中纵向模态以轴对称方式传播,具有径向和纵向位移分量,不存在环向位移分量,相比其他模态更容易激发.纵向模态传播如图1 所示,式(1)为频率方程,在已知圆柱杆参数下可求出频散方程的解.

图1 实心圆柱杆纵向模态示意图

1.2 钢筋频散曲线

钢筋直径12 mm,弹性模量210 GPa,泊松比0.3,密度7 850 kg·m-3,采用MATLAB 环境下开发的PCDISP 软件[17],求解频散方程的数值解,得到各模态频散曲线,如图2 所示.

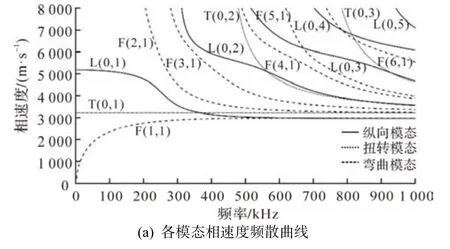
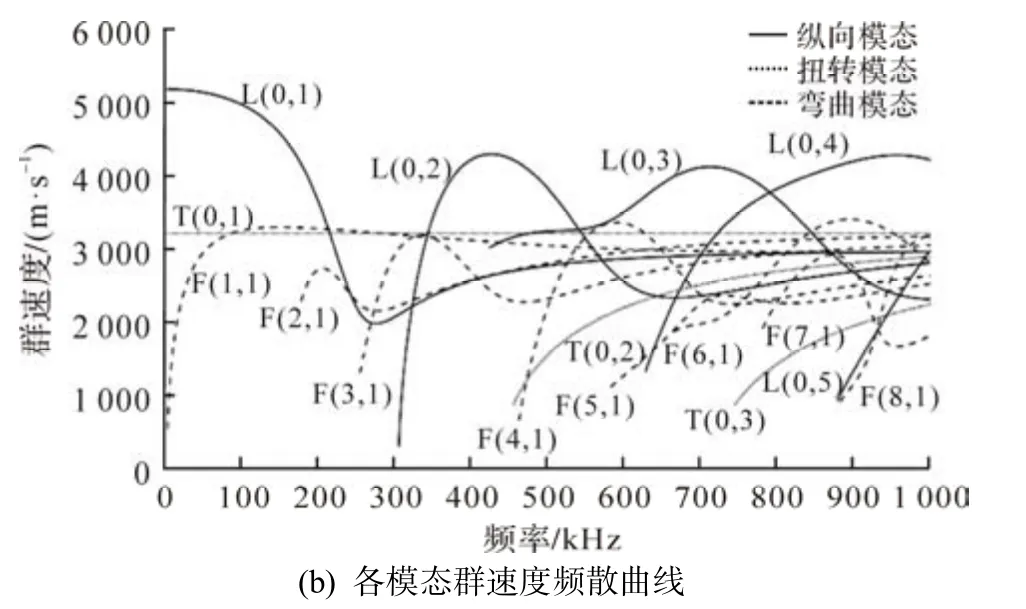
图2 钢筋各模态频散曲线

从图2 可见,超声导波模态数量随着频率增加而增加,选择合适的激励频率可减少频散现象,有利于检测.

本文选择频率为100 kHz,将超声波换能器布置在钢筋端部,此时主要激发纵向模态,根据L(0,1)模态的声波参数变化判断钢筋损伤情况.但由于钢筋两端换能器不能保证完全对称布置,需要考虑弯曲模态F(1,1)存在,下文简称L 波和F 波.

1.3 反射系数定义

反射系数指损伤反射回波信号与首波信号的幅值比值,表征损伤程度对损伤回波信号幅值的影响,通过该系数确定钢筋损伤状况,定义为:

式中:C为反射系数;A1为损伤反射回波信号幅值;A2为首波信号幅值.

2 钢筋机械损伤检测

2.1 试验平台搭建

RIGOL-DG1022Z 任意函数信号发生器和RIGOL-DS2102A 示波器(普源精电科技股份有限公司),DYZ-300-01A 超声波换能器(福州大禹电子科技有限公司).采用Rigol Ultra Station 软件,利用汉明窗函数调制5 个周期正弦波作为激励信号,中心频率100 kHz、最大幅值±5 V、波形总时长50 μs、采样点3 000 个.激励信号u表达式为:

式中:U为需要调制的激励信号最大幅值;f为中心频率;t为时间.

试验选择直径12 mm 的HPB300 热轧光圆钢筋,长度90 cm,钢筋两端截面用砂纸打磨使其平整.AB 胶作为耦合剂将钢筋与超声波换能器固定,粘贴过程中注意与换能器均匀接触,最大程度降低信号泄漏.与信号发生器相连的换能器具有发射功能,由材料的压电效应将电信号转换为机械振动传递;与示波器相连的换能器具有接收功能,将机械振动转化为电信号,由示波器接收电信号并显示波形.每根钢筋经过多次测量得到数据,选择波形和幅值稳定的信号研究,以减小误差.

奈奎斯特(Nyquist)定理规定采样频率是信号最高频率的10 倍及以上时,采集的信号基本可以还原原始信号.综合考虑示波器中可选择的参数,选择采样率10 MHz,采样时间1 400 μs.

2.2 不同深度机械损伤

距离钢筋发射端面70 cm 处,用钢锯切割宽度1 mm,深度分别为1、3、5、7、9、11mm 的损伤.对不同损伤深度的钢筋(包括无损伤钢筋)编号A1～A7,机械损伤如图3 所示.

图3 钢筋机械损伤加工

由于机械损伤的存在,时域中会出现损伤反射回波,主要考虑2 条传播路径: 超声导波从发射端面发出后到达机械损伤处,部分波被反射回发射端面,继续反射后到达接收端面被换能器接收,称为损伤前反射回波;其余部分未受机械损伤影响而直接到达接收端面,再回到损伤处后经反射回到接收端面被换能器接收,称为损伤后反射回波.传播路径如图4 所示.

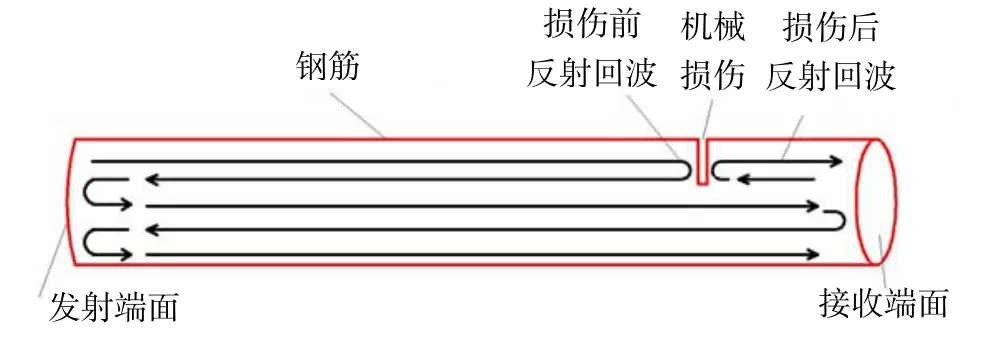
图4 钢筋在机械损伤下的超声波传播路径示意图

在MATLAB Signal Analyzer 中使用bandpass函数对得到的信号进行带通滤波处理,阻带衰减60 dB,陡度0.85.经处理后的信号解决了基线偏移现象,使信号变得光滑.根据钢筋各模态频散曲线(图2)可知,L(0,1)的理论波速大于F(1,1).选取时域前700 μs,考虑损伤的存在,因此时域中将依次出现L 首波、F 首波、L 损伤后反射回波、F 损伤后反射回波、L 损伤前反射回波和L 端面反射回波.选取具有代表性的钢筋编号A1、A4、A7 时域(图5),统计各波幅值与钢筋损伤深度的关系,结果如图6 所示.

图5 钢筋不同机械损伤深度时域

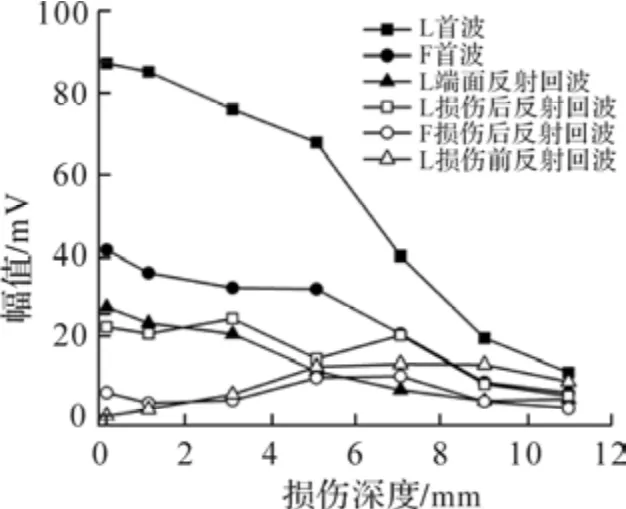
图6 机械损伤深度与信号幅值的关系

钢筋在无损伤情况下,信号在钢筋两端来回反射直至衰减,对于L 和F 首波后的一系列波形,推测由导波在钢筋界面的反射、折射而发生模态转换形成(图5(a)).随着损伤深度增加,L 首波、F 首波和L端面反射回波幅值均逐渐减小,导波受损伤干扰,时域中波形不再单一,波与波之间发生叠加,导致难以分辨.损伤深度为5 mm 时,各损伤反射回波明显可见(图5(b));损伤深度达到11 mm 时,超声导波在损伤处不断发生反射、折射、衍射,使能量大幅度衰减,L 损伤前反射回波在时域中突显,此时F 波幅值大幅度减小,以至于时域中难以观察(图5(c)).

由各模态群速度频散曲线可知,导波纵向模态在频率100 kHz下的理论传播速度为4 951.3 m·s-1.为研究不同机械损伤深度对导波波速的影响,采用飞行时间法计算导波实际传播速度,并与理论波速进行对比.计算过程如下:

(1)时域中找到L 首波和L 端面反射回波的位置,并记录波峰值出现时间.

(2)假设L 首波峰值出现时间为t0,L 端面反射回波峰值出现时间为t1,则t1-t0就是L 首波被接收端换能器接收到后信号反射回发射端,再从发射端反射到接收端所需时间,这段时间对应的路程即2 倍的钢筋长度.

(3)设钢筋长度为l,则L波实际传播速度vL为:

不同工况下L 波实际波速计算结果见表1.从表1 可发现,采用飞行时间法计算得到的L 波实际波速随损伤深度增加基本无变化,且与理论波速误差均在1.25%内,表明机械损伤的存在对钢筋中导波传播速度几乎无影响.未被损伤阻挡的波可直接传播至接收端面.

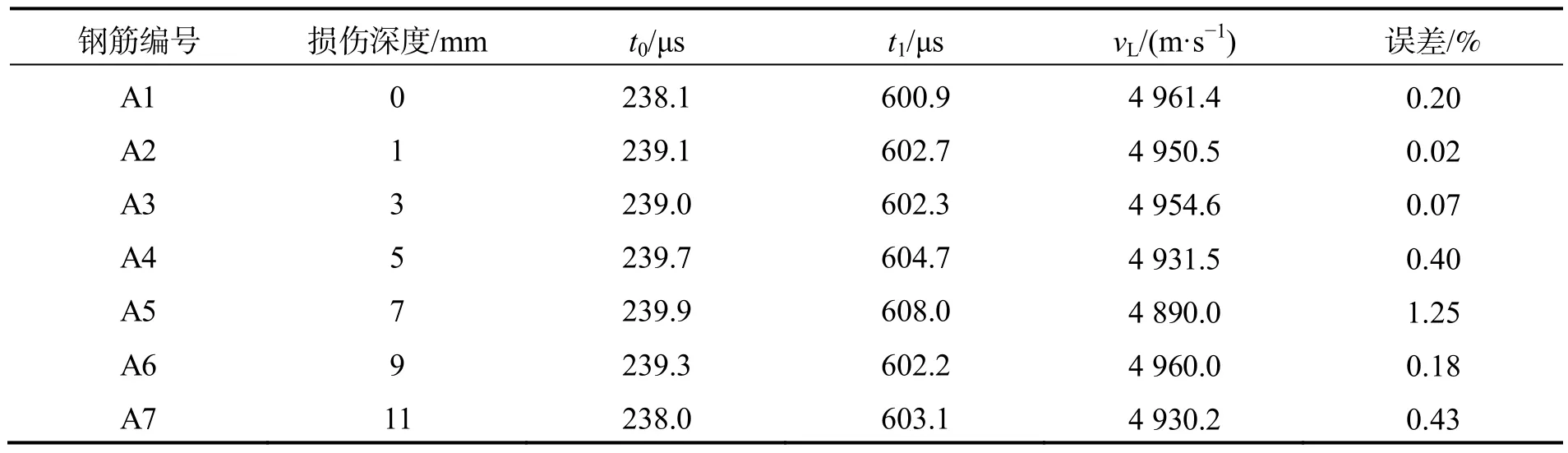
表1 不同机械损伤深度钢筋实际波速计算结果

L 损伤前反射回波不与L 波和F 波发生叠加,可在时域中清晰显示.对其进一步研究发现,L 损伤前反射回波理论上第一次被接收到传播路程为7 0+70+90=230 cm,选择A5 钢筋进行验证.L 损伤前反射回波峰值出现时间与L 首波峰值出现时间相差519.9－239.9=280.0 μs,与计算得到的L 波实际波速相乘可得到L 损伤前反射回波比L 首波多传播的距离为280.0×4890.0=136.9 cm.已知L 首波的传播距离为钢筋长度(90 cm),由此求出L 损伤前反射回波的实际传播距离为136.9+90=226.9 cm,与理论路程对比,误差仅1.37%.

从图6 可发现,随着机械损伤出现,L 损伤前反射回波幅值先增加,损伤深度达到约钢筋直径一半时,损伤界面的存在导致波传播路径被阻断,导波能量传递效率大幅降低,首波幅值的降低不可避免导致损伤回波幅值降低.计算不同损伤深度下损伤前反射回波的反射系数,结果如图7 所示.从图7 可知,反射系数随损伤深度增加逐渐增大,采用MATLAB 软件进行数值拟合得反射系数C与损伤深度x呈线性关系(C=0.08209x-0.15251,R2=0.93927).在检测中可以通过计算反射系数实现对损伤程度的定量分析.

图7 机械损伤下L 损伤前反射回波反射系数的计算

2.3 不同位置机械损伤

确定钢筋一端为连接换能器后的超声导波发射端,分别在距离发射端不同位置处用钢锯加工深度5 mm、宽度1 mm 的损伤,对不同损伤位置钢筋编号为B1～B7,距离发射端分别为10、20、30、45、60、70、80 cm.

试验发现,当损伤位置关于钢筋中点对称时,时域中波形十分相似.因此选取有代表性的钢筋B1～B5 时域,结果如图8 所示.从图8 可发现,损伤位置距离钢筋中点越近,L 损伤前反射回波与L损伤后反射回波出现的时间越接近.B4 时域中,L损伤前反射回波与L 损伤后反射回波的传播路程均为180 cm,在同一时刻出现并发生叠加,损伤反射回波幅值明显大于其他工况.当损伤位置关于钢筋中点对称时(图8(c)和图8(e)).B3 时域中L 损伤后反射回波和B5 时域中L 损伤前反射回波的传播路程均为210 cm,因此时域中出现位置相似.此时在损伤位置未知时,计算得到损伤回波传播路程后无法判断其传播路径,因而无法准确计算出损伤位置.选择时域图中受其余波干扰较小、时间靠后出现的L损伤反射回波,计算得到反射系数如图9 所示.

图8 钢筋不同机械损伤位置时域

图9 钢筋中点对称损伤位置的反射系数

从图9 可发现,对于损伤位置关于中点对称的钢筋,损伤位置距离接收端较远的反射系数比距离接收端较近的更大,因此在实际计算损伤位置时,需要先测一次信号,之后将超声波换能器对调后连接,再测一次信号,即原本的信号发射端变成了接收端.通过比较L损伤反射回波的反射系数大小可确定损伤是否远离接收端,最后再计算传播路程,得到损伤的具体位置.

3 钢筋锈蚀损伤检测

3.1 点锈蚀损伤

选择直径12 mm、长90 cm 钢筋进行特殊处理,在距离钢筋端部70 cm处套上直径5.2 cm的塑料杯,接触位置涂抹AB 胶防止溶液渗出,将5%NaCl 溶液倒入杯内.采用汉普公司HSPY-60-03 直流电源,铜棒放入杯中并连接电源负极,导线接在钢筋中间并连接电源正极.接通电源后,杯中钢筋发生加速锈蚀,没有与溶液接触的钢筋则无变化,以此达到点锈蚀的效果.试验过程中及时清理塑料杯中的锈蚀物并更换NaCl 溶液,避免锈蚀物堆积导致锈蚀速率减小,点锈蚀总体布局如图10 所示.设置直流电源电流为500 mA,每12 h 停止通电并进行超声波测试.

图10 点锈蚀试验设计

锈蚀时间156 h 时停止试验,钢筋损伤如图11所示.点锈蚀处钢筋直径大幅减小,存在不同宽度、深度的不规则锈坑.而钢筋机械损伤的损伤界面较平整,两者对导波反射有较大差别,点锈蚀下的超声波传播路径如图12 所示.

图11 钢筋点锈蚀损伤

图12 钢筋在点锈蚀下的超声波传播路径示意图

试验发现,时域中各类反射回波幅值随锈蚀时间的变化较小,与机械损伤相比较难观察到,因此选择不同锈蚀阶段的时域(图13),锈蚀时间分别为12、48、156 h,统计点锈蚀时间与信号幅值关系如图14 所示.从图14 可发现,随着锈蚀时间的增加,L 首波幅值先小幅增加后减小,L 损伤前反射回波逐渐增大.

图13 钢筋点锈蚀时域

图14 点锈蚀时间与信号幅值的关系

图15 为点锈蚀下L 损伤前反射回波反射系数.从图15 可发现,锈蚀时间为0～36 h 时,反射系数增加缓慢,此时对于宽度较大、深度小的锈坑,导波在锈坑边界反射具有随机性,能量向各方向衰减,经钢筋端面反射后仅传递小部分能量;而对宽度较小、深度大的锈坑,经过锈坑后导波传递的能量相对较多,因此可以在时域中显示,如图13(a)时域中 400～550 μs 的杂波是由导波经深度较大的锈坑反射形成.锈蚀时间在36 h 后,反射系数增速加快,此时锈蚀导致钢筋直径减小,对反射回波影响占主导作用,损伤状况与机械损伤类似.此时L损伤反射回波在时域中可见(图13(b)),其出现且幅值增大是判断钢筋发生点锈蚀的关键.

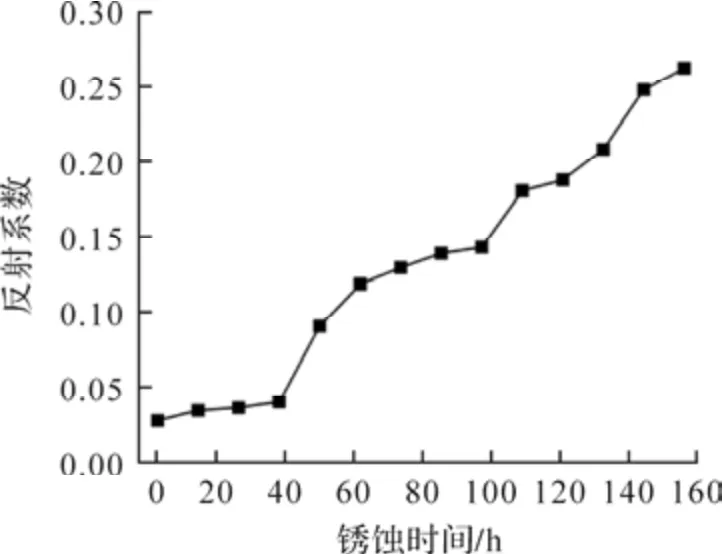
图15 点锈蚀下L 损伤前反射回波反射系数

对点锈蚀下波速进一步分析,计算结果见表2.锈蚀时间为0～120 h 时,L 波波速均与理论速度接近.随着点锈蚀程度的加重,L 端面反射回波波形明显改变,峰值出现时间滞后(图13(c)).锈蚀时间为156 h 时,波速减小至4 738.1 m·s-1,表明严重的点锈蚀对波速的影响不可忽视,可与机械损伤工况区分.因此在检测中可通过L损伤反射回波反射系数与波速的变化趋势判断点锈蚀程度.

表2 点锈蚀下实际波速计算结果

3.2 均匀锈蚀损伤

对直径12 mm(实测11.6 mm)、长60cm 的光圆钢筋整体进行加速均匀锈蚀试验,设定锈蚀率为0%、2%、4%、6%、8%、10%,每个试况3 根钢筋(锈蚀0%设1 根钢筋作为对照组),钢筋编号为C1～C16.钢筋锈蚀速率和锈蚀量可通过设置直流电源的电流大小和通电时间控制,锈蚀引起的钢筋理论质量损失依据法拉第定律计算:

式中:∆m为钢筋理论质量损失,g;ρ为钢筋理论锈蚀率,%;m为钢筋质量,g;M为铁的摩尔质量,取56g·mol-1;I为电流强度,A;t为通电时间,s;F为法拉第常数,取96485C·mol-1;Z为金属离子价数(Fe2+).

通过钢筋电流强度I可表示为:

式中:i为钢筋表面电流密度,mA·cm-2;s为钢筋表面面积,cm2;d为钢筋直径,cm;l为钢筋长度,cm.

本试验通电电流密度控制在2mA·cm-2左右,按式(7)计算所需电流强度为437.3mA.钢筋质量取平均值499.5g.按式(6)计算得到钢筋不同锈蚀率所需通电时间结果见表3.

表3 钢筋加速均匀锈蚀时间计算结果

当钢筋锈蚀率为10%时,锈蚀现象急剧加深,钢筋表面锈坑加深且分布不均匀,截面积明显减小,如图16 所示.

选取钢筋均匀锈蚀下部分时域(图17),从图17 可发现,均匀锈蚀下时域中波形无显著变化,没有复杂的损伤回波.锈蚀率为10%时,L 波和F 波的能量衰减相对机械损伤较小,L 波衰减率为47.2%,F 波衰减率仅为17.3%.这是因为均匀锈蚀损伤不像机械损伤那样有较大的损伤缺口阻断超声导波的传播,钢筋内部没有受到外表面锈蚀的影响,导波能量损耗较少.

对导波波速进一步计算分析结果见表5.随着锈蚀率增加,L 波波速逐渐增加,推测由于锈蚀后钢筋直径减小、表面物质改变以及众多锈坑的存在影响了超声波模态,致使波速发生改变.因此在检测中可通过波形与波速变化作为钢筋是否发生大面积均匀锈蚀的依据.对于均匀锈蚀损伤的定量分析则需进一步研究.

3.3 基于小波变换的钢筋损伤时频分析

小波变换在短时傅里叶变换基础上进一步发展而成,继承了短时傅里叶变换的局部化思想,并解决了时间窗的大小不能随信号频率的变化而变化的问题.小波变换采用时间-尺度域,尺度与频率成反比,尺度越大,采用的时间窗越大[18].对任意函数f(t) ∊L2(R),连续小波变换表达式为:

式中:ψ(t)为母小波函数;a为尺度因子;b为平移参数.

对不同损伤工况下的钢筋得到的超声导波原始数据进行基于连续小波变换的时频分析.在MATLAB 软件中使用cwt()函数,由此产生的时频表示也被称为Scalogram,表示信号的连续小波变换系数绝对值.时频图同时表征信号的时间、频率和能量参数,通过图谱中颜色的改变可快速得到时域中信号各部分能量大小和分布范围,以此判断钢筋损伤程度和损伤类别.

选取无损伤钢筋、机械损伤深度11mm、钢筋点锈蚀时间156h、钢筋均匀锈蚀率10%共4 组数据,进行连续小波变换得到的时频如图18 所示,小波函数选择Morse 小波,频率以对数比例绘制.

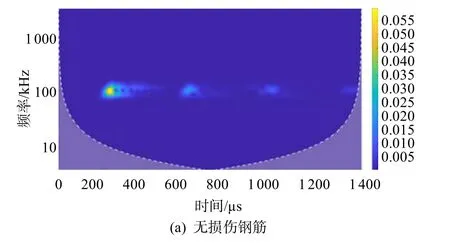
图18 钢筋不同损伤时频分析

时频图中右侧为能量谱,从上至下能量数值依次减小,表征导波所含能量相对大小.每一个波包对应一个能量包络,信号存在的地方显示能量包络,最明亮的色块主要集中在主频100 kHz,表明此处能量最大,时域中对应L 首波.

无损伤时频图中,能量集中在L 和F 首波以及之后一系列端面反射回波中,分布规律明显,能量最大值0.059.机械损伤时频图中,能量明显集中在L 首波和出现时间约为520μs 的L 损伤前反射回波处,能量相比无损伤钢筋衰减明显.复杂损伤回波的存在使色块分布极不均匀,遍布整个时域.点锈蚀时频图中,除L 首波外能量逐渐分散,时间300～700μs 时可以观察到各种损伤回波的色块在横向和纵向分布,其能量明显小于机械损伤时情况.均匀锈蚀与钢筋无损伤时频图相似,能量主要集中在L首波以及之后的端面反射波,但能量最大值远小于钢筋无损伤时,仅为0.032.根据以上特点,依据由连续小波变换的时频图可简单分析钢筋的损伤状况,节省处理数据时间.

4 结论

(1)钢筋机械损伤试验中,L 首波、F 首波、L端面反射回波幅值随损伤深度的增加逐渐减小,机械损伤对导波传播速度几乎无影响.根据L损伤前反射回波的反射系数与损伤深度的拟合曲线可对损伤程度进行定量分析.通过确定L损伤反射回波出现时间,在已知波速情况下精确计算其传播路程.考虑损伤位置关于钢筋中点对称,比较L 损伤反射回波的反射系数大小判断损伤是否远离钢筋发射端,最终可得到具体的损伤位置.

(2)相比机械损伤,在钢筋锈蚀损伤试验中导波能量衰减较小.L 损伤反射回波出现且幅值逐渐增大可作为钢筋发生点锈蚀的依据,结合反射系数与波速变化趋势判断点锈蚀程度.均匀锈蚀中波形无显著变化,L 波波速有逐渐增加趋势,在锈蚀率为10%时增加至5 069.7 m·s-1,以此作为判断钢筋是否发生大面积均匀锈蚀的依据.

(3)基于连续小波变换得到时频图,根据图谱中各部分的能量大小和分布范围可以简单分析钢筋的损伤状况,节省处理数据时间.