考虑硫沉积影响的水平井稳产能力预测

王勇飞，刘言，梁中红，向祖平

（1.中国石化西南油气分公司采气二厂，四川 南充 637000；2.中国石化西南油气分公司，四川 成都 610095；3.重庆科技学院，重庆 400041）

0 引言

四川盆地高含硫气藏储量规模较大，大部分气田产出流体中含有硫化氢气体组分［1-2］。开采过程中，溶解在天然气中的部分硫颗粒随着压力降低而析出，同时，由于井底附近压力降低幅度比较大，井筒附近形成大量的硫堆积，降低了天然气渗流能力［3-4］。为了合理地制定开发方案并对储层进行评价，需要建立相应的数学模型描述高含硫气藏水平井渗流过程，以模拟气井稳产时间、井底压力和地层压力的变化。

目前，许多学者采用径向复合模型来描述高含硫气藏流动规律。2006 年，李成勇等［5］提出了无限大外边界径向复合高含硫气藏井底压力模拟模型。2008 年，张烈辉等［6］考虑硫沉积影响，建立了双区复合稳态产能模型。考虑储层为双重介质模型，晏中平等［7］建立了双孔介质硫沉积影响的试井解释数学模型。考虑流体在井筒中的相分离，王海涛等［8-9］分别建立了径向复合渗流数学模型来描述气渗流规律。考虑大的缝洞性碳酸盐岩气藏，魏操等［10-11］建立了井洞相连的串珠状缝洞型油藏试井模型。上述学者利用径向复合模型对高含硫气藏直井不稳定渗流规律进行了研究，但没有基于不稳定渗流模型开展稳产能力预测研究。

2013 年，党勇杰等［12］基于稳态产能模型开展了带状高含硫气藏分支水平井产能预测研究。李继强等［13］基于实验对高含硫气藏PVT 属性进行了分析，结合数值模拟技术模拟高含硫气藏动态变化特征。崔明月等［14］基于非稳态椭圆流理论，建立了压裂水平井高含硫气藏非稳态产能预测模型。同时，也有一部分学者对高含硫气藏气井见水时间、 水平段长度优化和产能预测进行了研究［15-17］。

然而，目前还没有高含硫气藏水平井稳产能力预测方面的研究。为了对高含硫气藏水平井进行准确的稳产能力预测，本研究将高含硫气藏分为内、外2 个区域，建立了矩形复合水平井不稳定渗流数学模型，采用边界元方法对其进行求解，并分析了井底压力变化规律；结合高含硫气藏物质平衡方程，建立了高含硫气藏稳产能力预测模型，分析各参数对稳产时间、井底压力和地层压力的影响，开展参数最优化和合理配产研究。

1 气藏数学模型的建立与求解

1.1 气藏物理模型

高含硫气藏开发过程中，井底压力降低，导致水平井井筒周围形成不规则的硫沉积区，由于硫沉积堵塞，部分水平井井筒单元没有渗流能力。本文采用复合模型来描述硫沉积形成（见图1）。其中：内区为硫沉积区，渗透率和孔隙度分别为K1，ϕ1；外区为非硫沉积区，渗透率和孔隙度分别为K2，ϕ2；Γin为硫沉积区边界，Γout为非硫沉积区边界。为了更好地建立相应的数学模型，基本假设条件如下：1）天然气在储层中的渗流为等温渗流；2）气井定产量生产，且投产前地层处处压力相等；3）流体为单相流，且不考虑重力和毛细管力的影响；4）流体流动满足达西渗流规律。

图1 考虑硫沉积水平井物理模型示意Fig.1 Schematic diagram of physical model of horizontal well considering sulfur deposition

1.2 渗流数学模型

1.2.1 数学模型建立

根据实验研究，地层发生硫沉积时渗透率下降，硫沉积区渗透率与含硫饱和度的关系［18］为

式中：a 为经验系数（负值）；S0为含硫饱和度。

为了线性化渗流微分，用拟压力代表压力分别建立硫沉积区和非硫沉积区的无因次渗流数学模型。

1）硫沉积区渗流微分方程

2）非硫沉积区渗流微分方程

3）初始条件和外边界条件

4）界面衔接条件

式中：ψ 为拟压力，MPa/（mPa·s）；T 为储层温度，K；q˜为单位长度流量，104m3/d；h 为储层厚度，m；x，y，z 为计算点坐标，m；xw，yw，zw为渗流段中点坐标，m；Ct为综合压缩系数，MPa-1；μ 为气体黏度，mPa·s；t 为生产时间，h；n 为含硫区与非含硫区交界面法线向量；r 为平面径向距离，m；δ（x）为δ 分段函数；Z 为天然气偏差因子；p 为任意时刻的地层压力，MPa；下标1，2 分别表示硫沉积区和非硫沉积区；下标i 代表原始状态。

1.2.2 数学模型求解

为了方便方程求解，定义以下无因次变量：

式中：Q 为气井产量，104m3/d；Lr为参考长度，m；l 为长度，m；ω12为硫沉积区、非硫沉积区导压系数比；ϕ 为储层孔隙度；下标D 代表无因次。

对式（2）—式（7）进行无因次化处理，然后关于无因次时间进行Laplace 变化之后为

根据相关文献，式（8）和式（9）的通解［19-20］为

式中：K0（x）为零阶第一类贝塞尔函数；G1D（x），G2D（x）分别为硫沉积区、 非硫沉积区Laplace 空间无因次压力解；RD为三维空间下离散点与作用点的无因次距离。

根据边界元求解思路，分别将井筒、储层交界面和外边界分别离散为Nw，Nin和Nout个离散单元（见图2。其中：xmD为无因次水平井离散单元中点坐标，xD为无因次水平井离散单元节点坐标），详细的推导过程这里不再赘述，相关文献已经给出［21-22］。

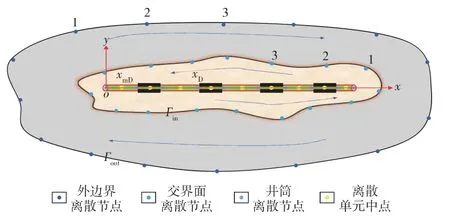
图2 井筒和边界离散示意Fig.2 Schematic diagram of wellbore and boundary dispersion

最终，基于边界元求解思想，式（8）和式（9）离散之后的渗流微分方程即式（15）和式（16）。

式中：θ1k，θ2k分别为内外区交界面、外边界离散单元节点处几何参数；为渗流离散单元无因次线流量；k 为离散单元节点编号；为离散单元节点在Laplace 空间下的导数；ξ 为边界元离散单元局部坐标［-1，1］内的任意一点；i 为离散单元序号。

不考虑流体在井筒中的压降，根据压降叠加原理，离散后的井筒与储层耦合方程为

式中：△xD为无因次水平井渗流段离散网格长度；ψwD为无因次井底压力。

根据质量守恒，得：

联立式（15）—式（18）构建矩阵，采用高斯消元法求解矩阵，最终得到无因次井底拟压力。

2 稳产能力预测模型构建

为了准确评估水平井开发高含硫气藏的稳产时间，需要结合油气藏物质平衡方程对地层压力和稳产时间进行评估。根据相关学者研究，定容高含硫气藏物质平衡方程［23-24］为

式中：G 为动态地质储量，104m3；Gp为累计产气量，104m3；ρs为固体元素硫密度，g/m3；Rs为当前压力下硫在含硫气体中的溶解度，g/m3。

气井定产量生产时，物质平衡拟时间（ta）为

具体模拟计算方法及步骤如下：1）给定气井生产时间数组，设定气井定产生产产量为qconst，计算任意时刻的累计产气量；2）根据式（19），计算任意时刻的p/Z，通过p/Z 关系曲线插值计算p；3）根据已知地层压力计算任意时刻的μ，Ct，Rs［14］，再根据式（20）计算任意时刻的ta；4）根据无因次时间定义，计算无因次物质平衡拟时间；5）利用无因次物质平衡拟时间，计算Laplace空间无因次井底压力（式（15）—式（18））；6）利用Stehfest数值反演［25］得到实空间下无因次井底压力，再根据无因次压力定义、拟压力与压力关系曲线，得到任意时刻井底压力pw；7）将计算得到的井底压力与设定井底压力pw_const对比，当相对误差绝对值小于1e-5 或模拟时间结束时停止计算。否则，重复步骤2）—6）。

3 参数敏感性分析

假定所有渗流段、堵塞段的长度相等，利用上述方法计算井底压力和平均地层压力，基本参数见表1。

表1 稳产能力预测基本参数Table 1 Parameters for prediction of stable production capacity

从图3 可以看出：含硫饱和度越大，水平井井筒周围越容易形成硫沉积，天然气在井筒周围的渗流阻力就越大，气井稳产时间越短。同时，受井筒周围硫沉积的影响，定产量生产情况下储层流体补给能力减弱，因此，含硫饱和度越大，定产阶段井底压力下降速度越快。通过回归气井稳产时间与含硫饱和度数据发现，含硫饱和度与稳产时间呈指数递减关系，表明含硫饱和度的增加对气井稳产时间的影响比较大。

图3 含硫饱和度对稳产时间和井底压力的影响Fig.3 Effect of sulfur saturation on stable production time and bottom hole pressure

从图4 可以看出： 堵塞段与渗流段长度比值对稳产时间和井底压力有比较明显的影响，堵塞段与渗流段长度比值越大，说明硫沉积导致大部分水平井筒外部堵塞，流体流入井筒的通道越少，稳产时间越短。同时，回归稳产时间和堵塞段与渗流段长度比值发现，两者呈很好的负线性关系。

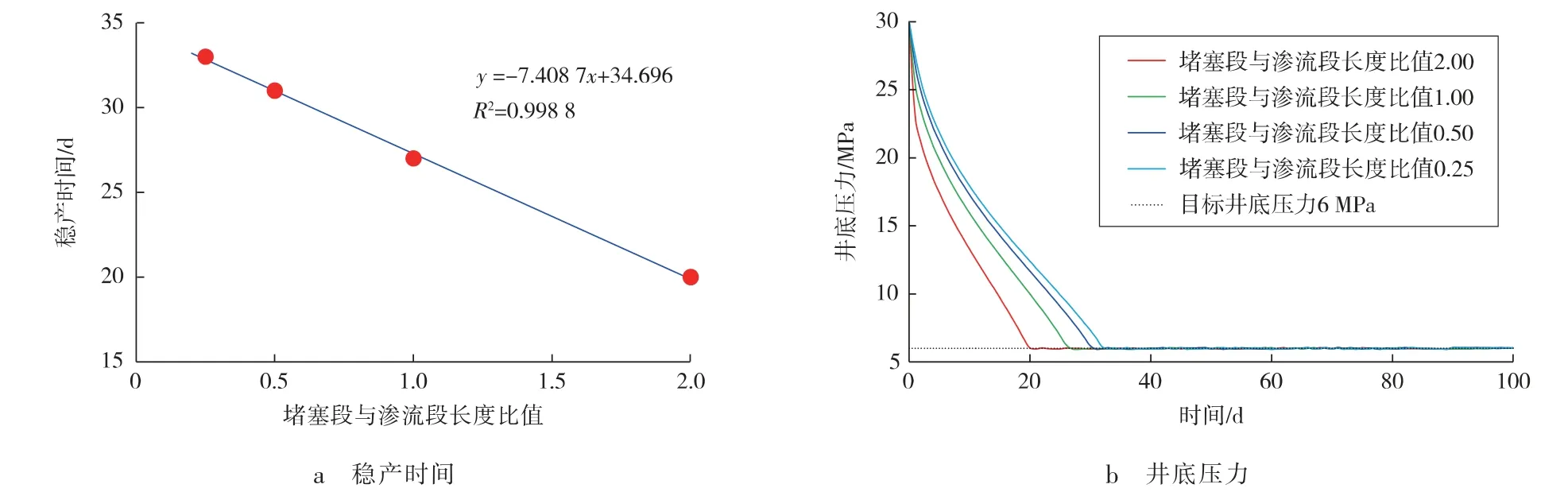
图4 堵塞段与渗流段长度比值对稳产时间和井底压力的影响Fig.4 Effect of blocked and seepage section length ratio on stable production time and bottom hole pressure

从图5 可以看出： 水平段长度对稳产时间和井底压力的影响较明显，水平段越长，渗流段越长，井筒与储层的接触面积越大，井筒周围渗流阻力越小，气井稳产时间越长。然而水平段长度与稳产时间并不呈线性变化关系，而呈指数变化关系，说明增加水平段长度对延长高含硫气藏稳产时间具有明显效果。

图5 水平段长度对稳产时间和井底压力的影响Fig.5 Effect of horizontal section length on stable production time and bottom hole pressure

4 实例分析

以四川盆地元坝高含硫气藏某水平井WH 为例。该井于2009 年3 月衬管完井，水平段长度为1 175.77 m。2010 年12 月该井开始投产，投产初期油压为48.09 MPa，日产天然气56.46×104m3，是一口典型的高产气井，井深6 645.4 m。原始地层压力为50 MPa，地层温度为154.79 ℃。2014 年7 月24 日关井测量压力恢复数据，关井前井底流压为42.28 MPa，产气量为60×104m3/d，压力恢复测试时间为7 d。气层有效厚度为108 m，孔隙度为0.057，井筒半径为0.083 m，气体相对密度为0.63。根据实验数据，该井硫质量浓度为2.098 g/m3，天然气组分摩尔分数见表2。

表2 元坝WH 井天然气组分Table 2 Natural gas components in Well WH of Yuanba gas reservoir

首先，基于Levenberg-Marquart 算法，用本文所建立的考虑硫沉积影响的水平井分段渗流数学模型对该井进行压力恢复数据拟合，拟合双对数曲线如图6 所示。从拟合结果可以看出，本文模型与实测数据拟合效果极佳，验证了模型的正确性。试井拟合得到水平井有效长度为912.30 m，堵塞段长度为263.47 m，渗流段个数为5，堵塞段个数为4，外推地层压力为42.66 MPa，表皮系数为0.5，井储系数为4.03 m3/MPa，等效硫沉积半径为997 m，含硫饱和度为0.25，储层渗透率为7.83×10-3μm2。

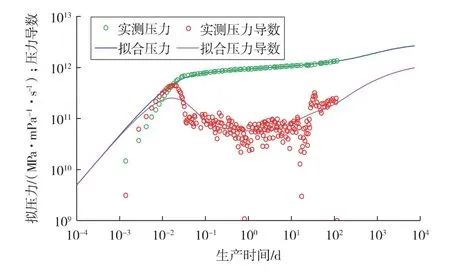
图6 WH 井压力恢复双对数拟合结果Fig.6 Fitting results of pressure build-up log-log of Well WH

其次，基于同样算法，采用定产气量的方法对井底压力进行拟合，并预测地层压力。拟合过程中，基于试井拟合得到的基本参数为初值，调整外边界大小，最终求得动态地质储量为27.41×108m3（见图7）。截至目前，地层压力为11.85 MPa，产气量基本维持在25×104m3/d。

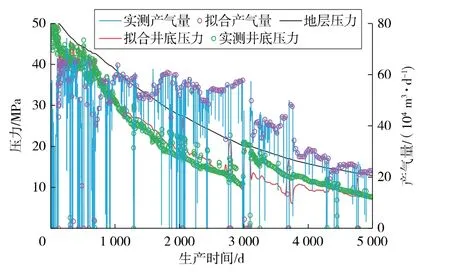
图7 WH 井生产历史拟合结果Fig.7 Fitting results of production history of Well WH

最后，基于生产历史拟合和试井拟合得到的基本参数，以当前状态进行稳产能力预测。预测当前状态下配产分别为25×104，20×104，15×104m3/d，目标井底压力为0.1 MPa 时气井井底压力和地层压力的变化（见图8）。

图8 WH 井生产预测结果Fig.8 Precdicted production results of Well WH

基于此，插值统计目标井底压力分别为0.1，3.0，5.0，7.0 MPa 时的稳产时间。从图9 可以看出，目标井底压力对气井稳产时间有很大影响，目标井底压力越小，稳产时间越长。在目前3 种配产方案下，气井最长可稳产440 d。

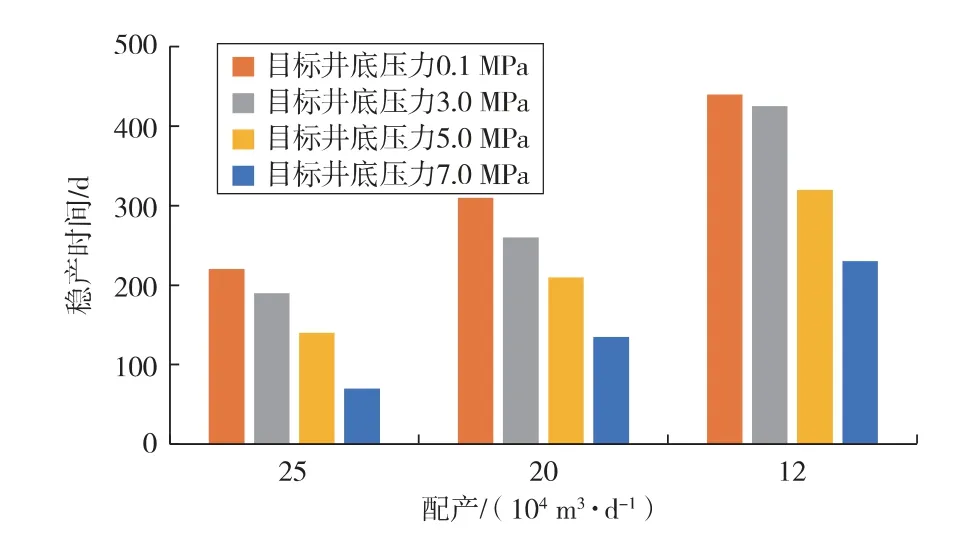
图9 WH 井不同目标井底压力下的稳产时间Fig. 9 Stable production period of Well WH under different bottom hole pressure

5 结论

1）结合边界元与源函数，对高含硫气藏水平井分段渗流数学模型进行求解； 结合不稳定渗流数学模型与高含硫气藏物质平衡方程，预测气井稳产时间和井底压力，为气井稳产时间预测提供了理论依据。

2）含硫饱和度、堵塞段与渗流段长度比值和水平段长度等对稳产时间和井底压力有着非常明显的影响，含硫饱和度和水平段长度与气井稳产时间呈指数变化关系。

3）通过对元坝高含硫气藏某水平井进行实例分析，验证了该方法的准确性和适用性。

4）气井整个生产周期都是定产生产与定压生产相结合的，建议开展高含硫气藏水平井变生产制度生产动态预测模型研究。