高山峡谷区山洪沟口泥沙堆积特征数值试验
2024-02-02聂一品王协康
聂一品,兰 玲,王协康
(四川大学山区河流保护与治理全国重点实验室,四川成都 610065)
中国有近一半的地区被划分为山洪灾害防治区[1]。山洪泥石流作为一种典型的山区地质现象,不仅有着广泛的分布[2],且频繁成灾。在以西藏东部为典型代表的高山峡谷地区,常存在高差大、海拔高且狭窄的山洪泥石流沟道[3]。在地质活动和地区气候环境的影响下,高原冰川发育,局地性暴雨强盛,松散堆积物厚度大[4],山洪泥石流活动频繁。受国民经济发展和可居住条件影响,高山峡谷沟口附近仍有大量的人类活动。山洪泥石流冲出沟道发生堆积会严重威胁地区人民生命财产和重大工程安全[5]。因此,众多学者利用现场调查、物理实验以及数值模拟的手段对山洪泥石流堆积体的物质组成、发展过程和致灾机理进行研究。Cenderelli等[6]通过对历史山洪泥石流事件的调查,发现堆积体的前缘和表面的泥沙颗粒的粒径通常是堆积体中最大的。针对2019年汶川“8·20”山洪泥石流事件,Li等[7]通过野外调查并结合影像分析,指出不当的人类活动加剧了山洪泥石流损失。Zheng等[8]基于系列泥沙堆积实验,表明了山洪泥石流释放流量的增加会显著地增大堆积体厚度和长度比值。王协康等[9]以2010年“8·13”文家沟山洪泥石流试验表明,受主流挤压作用,堆积体易在沟口形成多元堆积结构。Chen等[10]基于有限元特征的分裂算法建立了山洪泥石流堆积与干流交汇的模型,模拟了文家沟山洪泥石流的堆积过程。Han等[11]引入HBP流体模型,采用SPH方法模拟了2010年日本Yohutagawa山洪泥石流运动,获得了与现场调查一致的堆积体延伸范围。
综上,山洪泥石流堆积数值模拟大都是将多相流动视为单相流动[12],进而应用库伦塑性理论或黏塑性理论对流体流动进行描述[13],但忽略了不同大小颗粒流动过程的相互作用及其运动属性变化[14],难以揭示颗粒堆积过程致灾机理。离散单元法(DEM)作为一种能准确描述颗粒系统中颗粒之间的复杂的相互作用以及颗粒与周围环境之间的相互作用的数值模拟方法[15],能直接得到颗粒在运动过程中的动态信息[16]。计算流体力学方法(CFD)因其具有计算效率高、适用性好等优点,在地球表面的各种流体的计算中发挥着重要的作用[17]。为此,耦合CFD–DEM描述流体–粒子系统运动,已在研究颗粒系统的演进过程中成为了现实[18],例如滑坡坝破坏[19]以及山区河道泥沙输移[20]等。Li等[21]采用耦合CFD–DEM方法,研究了山洪泥石流对柔性防护网的影响,指出防护效率与山洪泥石流浆体弗劳德数密切相关。Fang等[22]结合CFD–DEM方法,评估了山洪泥石流对刚性防护结构的冲击特征,发现山洪泥石流固体体积分数的变化决定了防护结构上静荷载的分布。然而,耦合CFD–DEM方法对山洪泥石流的研究大都没有考虑其浆体流变特性的变化对颗粒运动的影响。为此,基于耦合CFD–DEM方法开展数值模拟,拟探究山洪泥石流体积浓度对不同粒径泥沙颗粒堆积过程中平均堆积距离和分散程度的差异,揭示了颗粒堆积分散程度随时间的变化规律,为理解山洪泥石流堆积致灾机理提供科学依据。
1 计算模型与研究方法
1.1 CFD–DEM耦合模型基本原理
采用CFDEM[23]耦合引擎耦合CFD开源软件OpenFOAM和DEM开源软件LIGGGHTS对高山峡谷区山洪沟口泥沙堆积形态及粒度特征进行计算。计算过程中使用的控制方程如下:
1)颗粒运动控制方程。颗粒运动主要考虑平动和转动。运动过程颗粒可能与邻近的颗粒和边壁发生碰撞或者与周围的流体产生相互作用进而实现动量和能量交换。因此,单个颗粒的运动可以通过牛顿第二定律进行描述,其控制方程可以写成:
式(1)~(2)中,mi为颗粒i的质量,v i为颗粒i的平动速度,Ii为颗粒的转动惯量, ωi为颗粒i的角速度,为其它颗粒或边壁作用于颗粒i上的接触力,为颗粒i通过颗粒–流体相互作用受到的作用力,为颗粒i的重力,M i,j为其它颗粒或边壁作用于颗粒i上的力矩。
2)流体运动控制方程。黏性不可压缩流体运动通过连续性方程和动量方程进行描述,其形式如下:
式中, αf为流体的体积分数,uf为流体的运动速度,ρf为流体的密度,p为流体的压强, τf为流体的应力张量,g为重力加速度,ffluid为流体平均下的颗粒通过颗粒–流体相互作用受到的阻力。
3)颗粒–流体间相互作用力控制方程。颗粒–流体相互作用力是由颗粒和流体之间相互运动而产生的黏性阻力,其大小与流体的流动状态和颗粒雷诺数有关。表达式为:
式中:Cd为阻力系数; χ为经验修正因子,χ=3.7-0.65exp(-(1.5-lgRep)2/2),其中,Rep为颗粒雷诺数。
1.2 模型及计算参数设置
1)模型设置
采用的概化高山峡谷区山洪泥石流沟道数值模型如图1所示。通过控制水箱中流体的高度,使不同体积浓度山洪泥石流在挡板下的出口处具有相同的压强。将粒径为1至2 mm的泥沙颗粒视为泥石流浆体的组成部分,使用单相流体模拟泥石流浆体的运动并结合流体体积分数(VOF)方法捕捉泥石流与空气的界面。挡板处于x= 0的平面上。流通区底部铺有厚度为0.1 m的卵砾石层,其粒径为6至24 mm。流通区和加速区比降为10%,长度分别为3m和1m。堆积区采用1%的比降,大小为6m×6m。模拟的总时间为20 s。
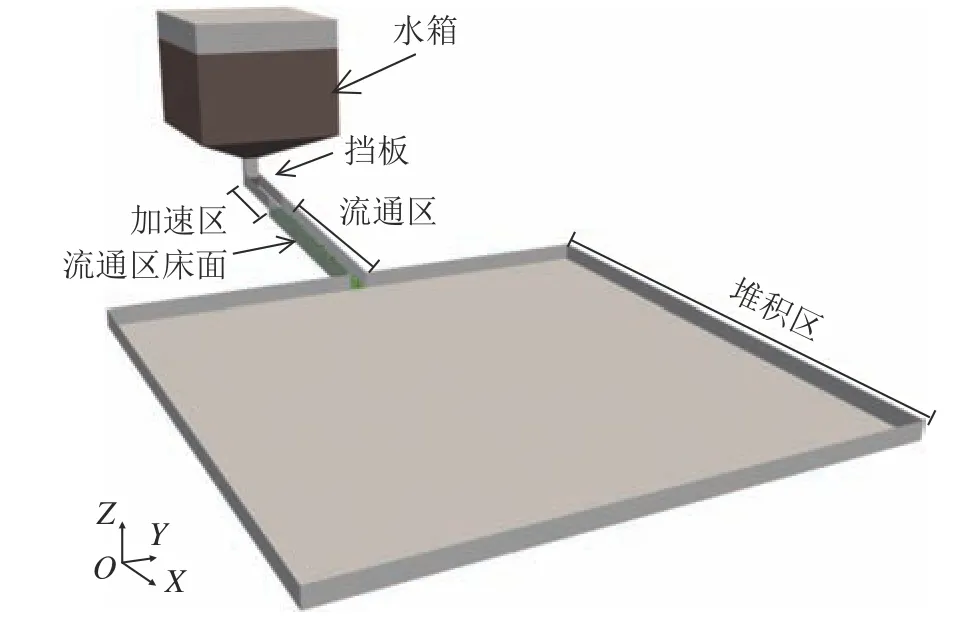
图1 典型山洪泥石流沟道数值试验模型Fig. 1 Numerical test model of a typical landslide gully
2)计算参数设置
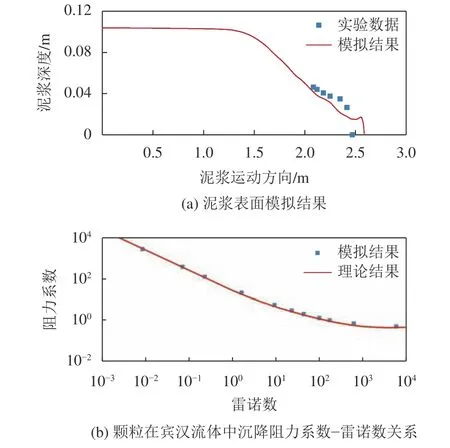
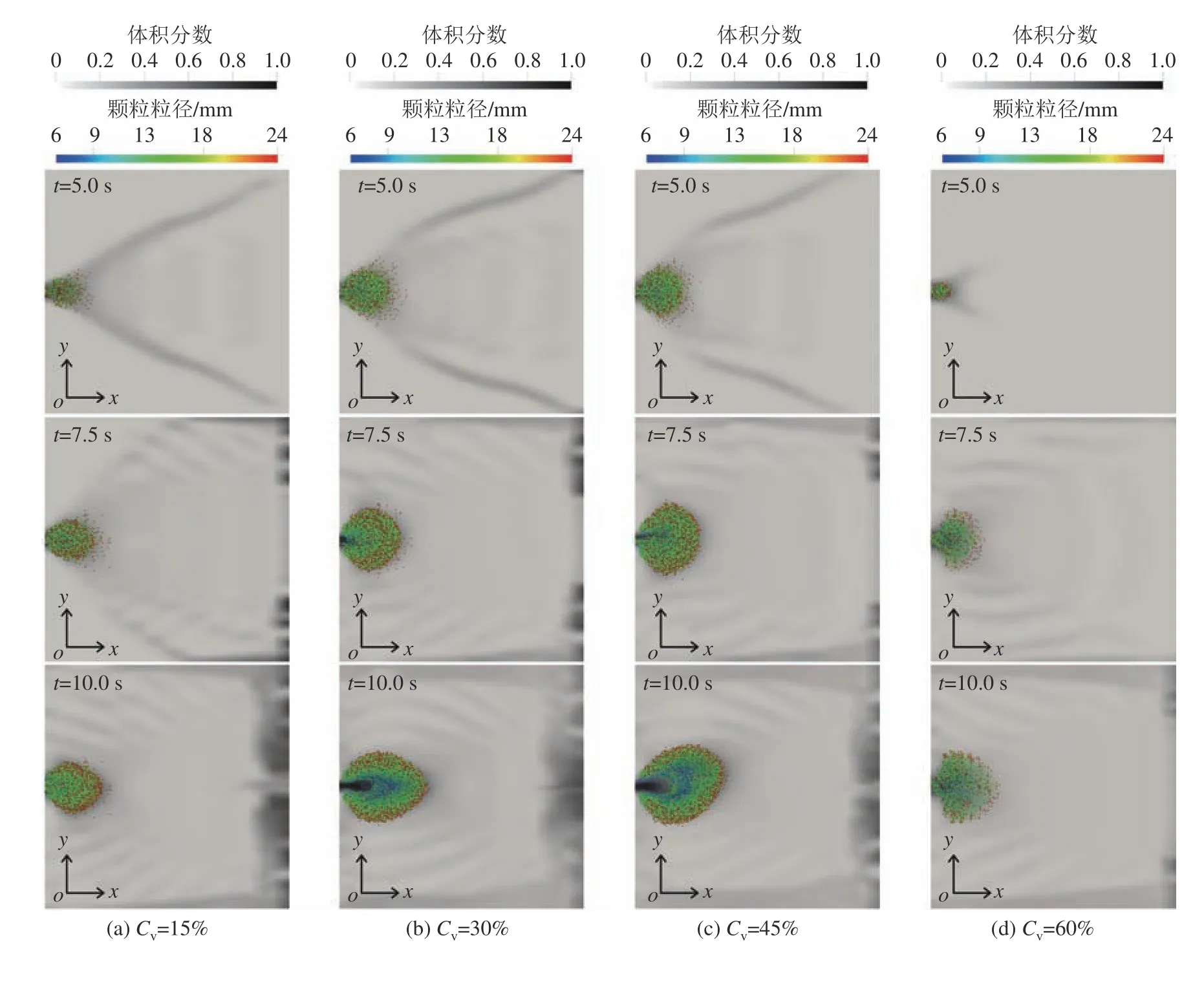
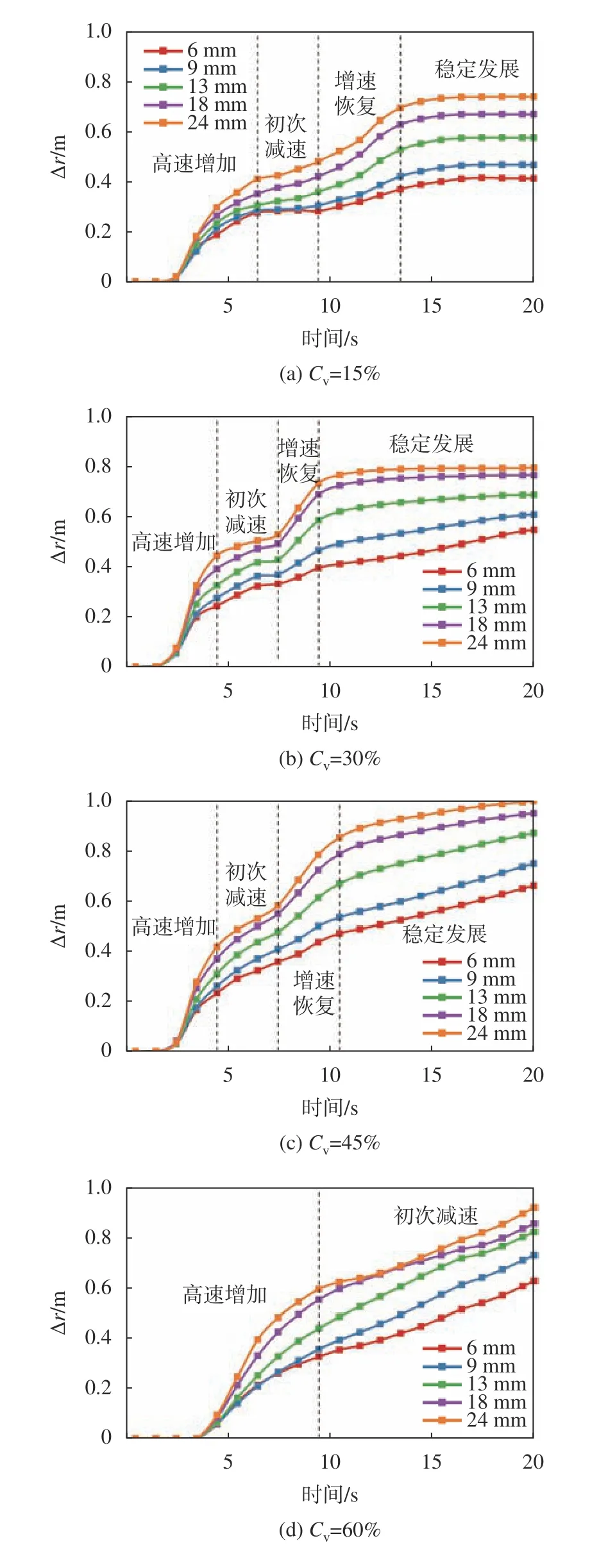
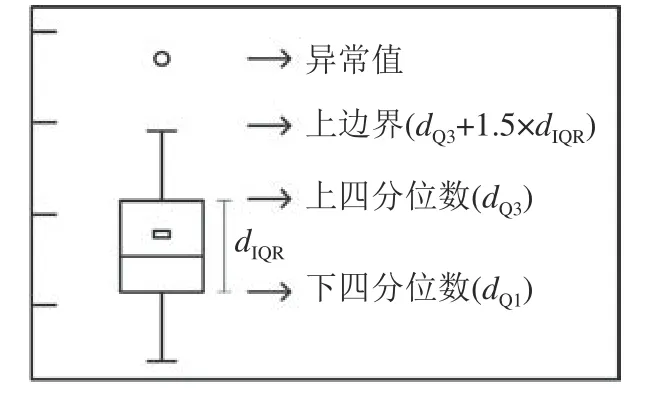
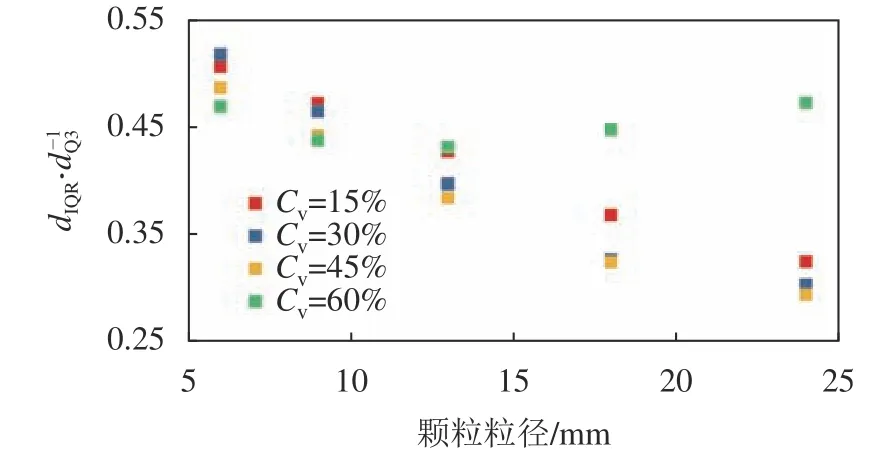
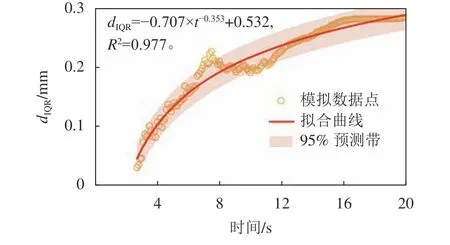
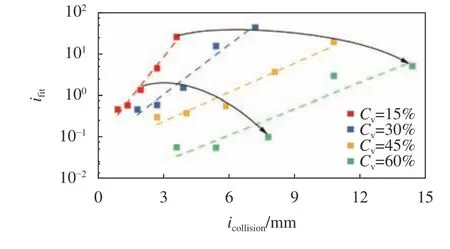
已有研究表明,山洪泥石流浆体的流变特性可以使用牛顿流体、宾汉流体、幂律流体以及二项式模式进行表述[24],而宾汉流体因其形式简单且具有较高的精度已经在山洪泥石流3维模拟中有着广泛的应用[11]。此外,已有大量研究对宾汉流体模型的流变参数进行了研究[12],故在本数值试验中使用宾汉流体模型对山洪泥石流的流变行为进行表达。试验中采用4种典型的山洪泥石流体积浓度(Cv)分别为15%、30%、45%和60%。在屈服应力的计算中,当体积浓度较低时采用文献[24]中的Kang和Zhang公式(0.15 表1 山洪泥石流浆体模拟参数Tab.1 Simulation parameters of debris flow 耦合模型中颗粒计算参数见表2。其中,颗粒之间的计算参数与颗粒和壁面之间的计算参数保持一致。 表2 耦合模型中颗粒计算参数Tab.2 Particle calculation parameters 使用泥浆溃坝实验来检验耦合模型对两相流体的交界面捕捉能力以验证模型的适用性。图2(a)绘制了Komatina[29]实验中第0.6 s时的泥浆表面和模拟结果。由图2(a)可见,模型对两相流体交界面的捕捉是较为准确的。随后计算颗粒在宾汉流体中沉降时阻力系数–雷诺数的关系来验证模型的准确性。经过模拟的阻力系数–雷诺数关系如图2(b)所示,其中理论结果选用Cheng[30]提出的公式。由图2(b)可见,模型能准确计算颗粒运动过程中颗粒–流体相互作用力。因此,耦合CFD–DEM模型可以准确地计算宾汉流体中颗粒的运动情况。 图2 CFD–DEM耦合模型验证Fig. 2 CFD–DEM coupling model validation results 计算开始后,床面泥沙颗粒在山洪泥石流的冲刷下发生运动。当泥沙颗粒运动到堆积区后,由于山洪泥石流速度降低,泥沙颗粒开始发生沉积。泥沙颗粒在堆积区中不同时刻的堆积的形态如图3所示,图3中,体积分数表明该时刻堆积区上山洪泥石流的运动痕迹。从图3(a)~(c)可以看出:体积浓度较低时(Cv≤45%),山洪泥石流冲刷的颗粒在初始堆积阶段(t=5.0 s),由于堆积平面足够大且没有阻挡物,泥沙呈现扇形堆积;随着山洪泥石流将更多的颗粒携带到堆积区中(t=7.5 s),堆积体堆积范围不断扩大,但依然呈现扇形分布。当Cv≤45%时,山洪泥石流对流通区床面的冲刷随着体积浓度的增加而增加[31],因此,在同一时刻下泥沙颗粒的堆积范围随着Cv的增加不断增加。在t=10 s时,由于Cv=30%和45%的模型中的床面已经被侵蚀完毕,因此在堆积区入口处,泥沙不断受到后续山洪泥石流的推动而产生空隙。在图3(d)中,沟床颗粒在Cv=60%山洪泥石流冲刷下形成的堆积体形态在堆积区与流通区交界处有一段很短的梯形堆积区域,随后扩展成半圆状。此时,由于山洪泥石流体积浓度很高,在运动过程中需要更多地克服黏性阻力,因此,堆积体发展的速度有所减缓。 图3 泥沙颗粒堆积过程模拟结果Fig. 3 Simulation results of sediment particle accumulation process 为了探究颗粒的粒径对其堆积行为的影响,分别计算了4种体积浓度下不同粒径颗粒与堆积体几何中心之间的距离( ∆r)随时间变化情况,计算结果如图4所示。从图4中可以看出,各粒径泥沙颗粒 ∆r随时间变化可分为4个阶段,分别为高速增加阶段、初次减速阶段、增速恢复阶段和稳定发展阶段。 第1阶段为高速增加阶段,该阶段中山洪泥石流从水箱中流出后在床面产生沿程冲刷,在流通区中产生了“龙头”,大量泥沙颗粒在聚集在山洪泥石流的前缘。当山洪泥石流到达堆积区时,“龙头”中的颗粒以很高的速度进入,导致 ∆r的高速增加。这一阶段中,山洪泥石流的冲刷使粒径较大泥沙颗粒运动速度显著快于较小的泥沙颗粒,因而当其进入堆积区后,大粒径泥沙的 ∆r增速大于粒径较小的泥沙。第2个阶段为初次减速阶段。在山洪泥石流的持续冲刷下,流通区床面颗粒不断受到侵蚀。但紧随“龙头”的后续浆体中泥沙含量相对较低,导致了 ∆r的增速减缓。 当流通区床面泥沙被山洪泥石流完全侵蚀后,处于堆积区中的泥沙颗粒在后续浆体的推动下产生整体性运动, ∆r随时间的变化进入到第3阶段即增速恢复阶段。这一阶段中,更大粒径泥沙颗粒的 ∆r增速依然大于较小的泥沙。此时,山洪泥石流浆体受到外围颗粒的阻挡,后续的浆体尚未从堆积体中流出。但随着模拟的进行,在某一方向上颗粒的堆积宽度减小,导致浆体从堆积体中流出,对堆积体的整体推动作用减小,形成了稳定发展的第4个阶段。Cv=15%时,稳定发展阶段的堆积体中颗粒的 ∆r最终不变,但随着Cv的增加, ∆r不再保持不变,其增速显著增大。在该阶段中, ∆r的增速随着粒径的减小逐渐增加,表明了在沟床的颗粒完全进入到堆积平面中后,由于山洪泥石流的持续作用,各个粒径的颗粒逐渐地混合在一起。Cv=60%的山洪泥石流的流动速度较低,到模拟结束时,沟床泥沙颗粒没有被完全侵蚀,因此,模拟中 ∆r随时间的变化仅有高速增加阶段和初次减速阶段。当Cv≤45%,随着Cv的增加,相同粒径的泥沙颗粒在同一时刻下的 ∆r逐渐增加,堆积体对堆积区的侵占更加严重。 图4 不同粒径颗粒距堆积体几何中心的平均距离Fig. 4 Average distance between particles of different sizes and geometric center of accumulation 模拟计算了大量(共计30577个)泥沙颗粒的运动数据,因此从统计的角度分析堆积区内颗粒运动的内在规律是可行的。将每一组模拟中颗粒的 ∆r按照绘制箱线图的方法进行统计。如图5所示,dQ1与dQ3分别代表经过统计得到的 ∆r的下和上四分位数。dIQR为四分位距,等于dQ1与dQ3的差值,反映了统计意义上 ∆r的集中趋势,可以表征颗粒在堆积体中分布的分散程度。上边界使用dQ3+1.5×dIQR表示,代表了非正态分布的 ∆r异常值的判别标准,用于表示堆积体外边界范围。经过统计分析,模拟过程中任何时刻异常 ∆r的数量都不多于8.5%,因此使用统计的方法得到的dQ3与dIQR和dQ3+1.5×dIQR来分别判断山洪泥石流堆积体中粒度特征和堆积范围是可以接受的。 图5 箱线图组成部分Fig. 5 Components of box plot 图6为堆积体中泥沙颗粒分散程度(dIQR)与泥沙颗粒的上四分位数(dQ3)的关系随粒径变化趋势,其中,dIQR/dQ3是将模拟过程中统计得到的dIQR与dQ3的数值相除后进行平均。 图6 颗粒堆积体中d IQR与d Q3之间的关系Fig.6 Relationship between dIQR and dQ3 由图6可知,当山洪泥石流体积浓度较低(Cv≤45%)时,dIQR/dQ3的值会随泥沙颗粒粒径的增加而不断的减小。这一现象说明,随着粒径的增大,泥沙颗粒堆积更加集中。此外,不同的dIQR/dQ3代表了各粒径颗粒在堆积平面上所处位置的不同。由图3(a)~(c)可知:在Cv≤45%的山洪泥石流冲刷形成的泥沙堆积体中,较大的泥沙颗粒显著地位于堆积体的外侧且各粒径颗粒在堆积体中的分选良好;Cv=60%时,堆积体中不同粒径颗粒的dIQR/dQ3不随粒径发生显著的变化,大致保持在0.45附近。这个现象表明,随着山洪泥石流体积浓度增加,各种粒径的颗粒较为均匀的混杂在堆积体当中。结合图3(d)可发现,即使当t=10 s时,堆积体的中心仍然可以明显看见大粒径泥沙的存在,泥沙颗粒之间的分选性较差。除粒径为6 mm的颗粒外,当Cv≤45%时,dIQR/dQ3随Cv的增加逐渐减小。这个现象表明随着山洪泥石流体积浓度的增加,泥沙颗粒的分选性逐渐变差。综合以上分析,堆积体中dIQR/dQ3的比值可以较为准确地代表各组分颗粒在堆积体内的相对位置,同时不同颗粒dIQR/dQ3数值的变化也表明了堆积体中颗粒之间具有良好的分选性。 图7为Cv=15%山洪泥石流冲刷下,粒径为6mm的颗粒在堆积过程中dIQR随时间的变化过程。由图7可知,随着时间的增加,dIQR的增速逐渐减小,且有接近一个最大值的趋势。由于被冲刷的泥沙颗粒需要一定的时间才能进入堆积区之中,故假设dIQR随时间的增长满足形如a×tb+c的幂函数关系。根据模拟数据点的分布情况,a和b都小于0,而c大于0。图7的预测带代表了dIQR在95%置信度上可能的范围,且几乎所有的模拟数据点都在95%预测带以内,这代表了幂函数关系对dIQR随时间的变化过程较为精准。结合图6的分析结果,可以在任意时刻通过dIQR的拟合结果,推断出dQ3的数值,从而估算山洪泥石流堆积体影响范围时间的变化过程。 图7 泥沙颗粒分散程度(d IQR)随时间变化过程Fig.7 Variation in the dispersion of sediment particles(d IQR)over time 所有模拟泥沙颗粒分散程度(dIQR)随时间变化过程的拟合参数与体积浓度(Cv)和粒径(d)之间的关系如图8所示。 图8 拟合指标i fit与碰撞指标i collision的关系Fig.8 Relationship between the ifit and icollision 图8中箭头的方向指示了不同模拟中同一粒径颗粒的拟合指标(ifit,即a×b/c)变化趋势。Cv的增加代表了山洪泥石流浆体内颗粒碰撞的几率的增加[32],而离散的颗粒与浆体中颗粒碰撞几率会随着颗粒粒径d增大而增大,故碰撞指标(icollision,即Cv×d)能代表离散的颗粒通过颗粒碰撞获得能量的几率大小。而a×b/c的增加则代表了颗粒的dIQR极值的减小和其增速的增大,也即代表着颗粒达到极限分散程度所需时间也较小。 粒径越大的泥沙颗粒可以通过碰撞能够获得更多的能量,其进入到堆积区后能在更短时间内克服较多摩擦阻力,实现更快的分散。随着Cv的逐渐减小,粒径较小的颗粒与浆体发生能量交换的几率大大减小,因此ifit随d的增益也越大。而当颗粒完成一定程度的分散之后,堆积体的存在导致了浆体的运动方向发生偏转,处于堆积体前缘的大颗粒难以被浆体推动,导致其分散状态难以继续改变,达到了极限分散状态。对相同粒径的泥沙颗粒来说,随着Cv的增加,浆体在运动过程中因其黏性消耗的能量不断增加,抵消了一部分传递给离散颗粒的能量,抑制了颗粒的分散。因此,如图8所示,同一Cv下,随着d的增大,ifit也随之增加,且Cv越小,a×b/c随d的增益也越大。而在同一粒径下,a×b/c会随着Cv的增加而呈现出先增加后减小的趋势。 基于高山峡谷区山洪泥石流沟道的特点,借助耦合CFD–DEM方法对沟口泥沙颗粒的运动进行了数值计算,重点研究了堆积体整体的形态及不同粒径颗粒的分布特征随时间的变化,主要结论如下: 1)随着山洪泥石流体积浓度的增加,泥沙堆积体的发展速度呈现先增加后减小的趋势,当体积浓度较高时堆积体的形态也随之发生改变。 2)不同粒径泥沙颗粒与堆积体几何中心之间的平均堆积距离( ∆r)随着模拟时间的变化呈现出4个不同的阶段。粒径的增大会导致堆积距离的增速增大,但随着运动的发展,各粒径颗粒堆积距离之间的差距会逐渐减小。 3)通过统计得到颗粒堆积距离的四分位距(dIQR)和上边界(dQ3+1.5×dIQR)可以表示堆积体中颗粒的分散程度以及堆积范围。不同粒径颗粒在堆积体中dIQR/dQ3的变化则反映了堆积体中分选性的良好与否。dIQR随时间变化的趋势的符合幂函数关系,通过拟合结果与dIQR/dQ3的数值变化规律可以得到任意时刻的泥石流堆积体的堆积范围。 4)相同体积浓度下,随着颗粒粒径的增加,颗粒的极限分散程度减小但能更快地分散。在颗粒粒径相同时,随着体积浓度的增加,颗粒的极限分散程度先减小后增加而分散速度先增加后减小。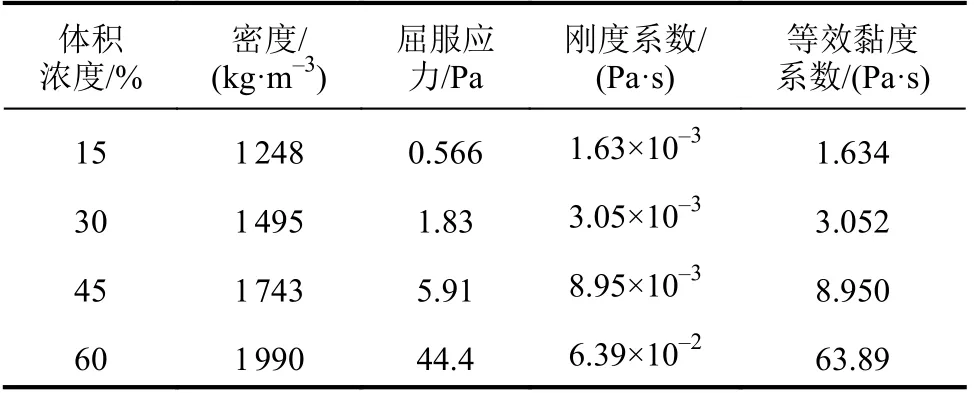

2 计算结果与分析
2.1 泥沙堆积形态的演变
2.2 颗粒平均堆积距离的演化
2.3 泥沙颗粒分散程度随时间的变化
3 结 论
