基于自抗扰与滑模理论的直驱永磁风力发电系统控制
2024-01-31蔡斌军李朝旗
蔡斌军,李朝旗,何 雍
(湖南工程学院 电气与信息工程学院,湘潭 411104)
随着环境污染、能源稀缺问题的凸显,各国致力于发展新能源产业,风力发电因具有清洁、高效、可持续和低成本的优点,成为新能源产业中的研究热点.近些年,在风力发电中,直驱永磁同步电机逐步成为研究热点[1].
风力发电技术的发展对风机的性能要求越来越高.在确保风机安全稳定运行的同时,改善风电质量,从而实现风力发电机最大功率输出.但直驱永磁风力发电系统的非线性、强耦合、风速不确定性及运行过程中受到多种干扰等特点为控制系统的设计带来了极大挑战.
目前,在风力发电系统中,采用较多的两种最大功率跟踪方法:一是最佳风力机特性曲线法;二是寻优法,如爬山搜索算法等.文献[2]在最大功率跟踪(MPPT)方法中引入了积分滑模控制方法,提高了系统响应速度,同时减小了超调和抖振问题.文献[3]采用线性自抗扰控制方法,算法简单,提高了转速跟踪能力,而且具备一定的抗干扰能力.文献[4]采用复合自抗扰控制方法,替代PI 控制器,在线性自抗扰控制器(ADRC)中引入非线性反馈,搭建了强线性误差反馈控制律和扩张状态观测器(NLESF+ESO)的复合型结构,提高系统跟踪速度和抗扰能力.文献[5]将滑模控制方法应用于并网逆变侧,电流内环采用动态滑模控制,减小了电流谐波,使系统具有较好的动态性能.
本文针对直驱永磁风力发电系统双PWM 控制技术展开研究.MPPT 采用叶尖速比法,机侧变流器转速外环采用自抗扰与非奇异终端滑模两种控制,对比其优缺点;网侧变流器采用传统PI 控制,实现母线电压稳定,并网功率独立解耦控制.
1 风力发电控制策略
1.1 风力机特性分析
由贝兹(Betz)理论可知,风力发电机仅使用部分风力发电,理论利用最大值为0.593,风机实际利用风能公式为
式中,R为风轮半径;λ为叶尖速比;V为风速;n为风机转速;β为桨距角;ωr为风机角频率;Pr为风机利用功率;Cp为风能利用系数;ρ为空气密度.
1.2 最大功率跟踪控制
根据式(1)、式(2)可知,风能利用率与风速、发电机转速、桨距角有关.在直驱风机中,发电机与轮毂直接相连,发电机转速变化直接影响风力机最大功率输出.在恒定风速下,转速恒定,则风力机输出最大功率;而当风速发生改变时,发电机转速跟随风速发生变化,从而实现最大功率跟踪.
1.3 机侧变流器控制
在三相静止坐标系下,永磁同步发电机数学模型复杂,难以准确建立.为了便于对永磁同步发电机的研究和控制,现对发电机进行下列假定:
(1)忽略铁芯磁饱和,不计铁芯的涡流和磁滞损耗;
(2)不计转子阻尼绕组;
(3)转子产生磁势为正弦波;
(4)定子绕组感应电动势服从正弦分布;
根据文献[6]建立在d、q 同步旋转坐标轴下的方程为
式中,ud、uq为d、q 轴定子电压;Rs为定子电阻;id、iq为d、q 轴的定子电流;Ld、Lq为d、q 轴的电感;ψf为磁链;ωr为发电机转子转速.
d 轴采用基于=0 磁场定向矢量控制技术,d、q 坐标系下永磁同步风力发电机电磁转矩为
式中,Te为电磁转矩;np为电机极对数;ψf为磁链.
电机系统动态方程可描述如下:
式中,Tm(N·m)为风机驱动转矩;J(kg·m2)为转动惯量.
1.4 自抗扰控制器
自抗扰控制器(ADRC)由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制律(NLSEF)三部分构成[6-7].
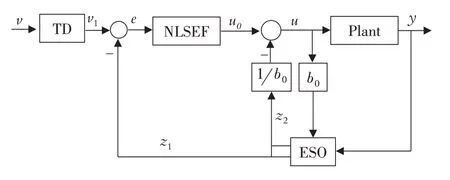
图1 自抗扰控制器结构图
非线性跟踪微分器事先安排过渡过程,使误差与误差微分反馈增益选取范围扩大,以此来降低系统的起始误差.
对于一阶系统:
式中,ω(t)为外部扰动值;f[ ]为系统的总扰动值;u为系统的控制量即电流iq.
由式(5)知,永磁同步风力发电机的速度环节为一阶系统,可得PMSG的一阶非线性微分跟踪器如下:
其中非线性函数fal 取为
式中,ν1是安排过渡过程后的速度信号;ωref是给定的速度信号;β0为控制跟踪信号快慢的变量,与跟踪速度成正比;δ为滤波.
对于一阶系统,扩张状态观测器的基本模型为
式中,z1是实际输出ω的观测值;z2是对系统总扰动的估计值;δ1为要调整的参数;e1为观测值z1与跟踪信号ω的误差值.
由非线性跟踪微分器式的输出和扩张状态观测器式的状态反馈得到系统的状态误差,并构建系统的非线性反馈控制律如下:
式中,e2为安排过渡过程后的信号ν1与实际输出ω的观测值z1的误差;-z2/b是补偿扰动的分量.
1.5 滑模控制器
滑模控制器(SMC)最主要的特点是控制量为不连续变化.该控制方法通过一定的控制策略让控制量不断地切换,迫使系统进入预先设定的滑动面进行运动,即滑动模态.由于滑动模态是可以设计的,且与系统的参数变化及外部扰动无关,因此具有鲁棒性强、可靠性高等优点.
SMC 设计包括两个步骤:滑动面的设计和控制律的设计.
1.5.1 非奇异终端滑模控制器的设计
系统的转速误差方程为
式中,ωref为发电机的最佳转速;ω为发电机的实际转速.
设计滑模面为
设滑模趋近率为
式中,k1,k2>0,0 <α<1.
由式(5)、式(13)(14)可得
1.5.2 稳定性分析
对于式(17),当且仅当s=0 时=0.综上,式(17)恒小于等于0.因此,所设计的趋近律满足滑模可达条件,即滑模控制器渐近稳定.
1.6 网侧变流器控制
网侧变流器在d-q 坐标系下的电压方程为[8]
式中,R为网侧线路等效电阻;L为网侧滤波等效电感;ud、uq为逆变器侧电压d、q 轴分量;id、iq为网侧电流的d、q 轴分量;ω为电网电流角频率;ed、eq为电网电压的d、q 轴分量.
实施PI 控制后的网侧变流器电压方程为
式中,Kp为比例系数;Ki为积分系数.
网侧变流器采用双闭环控制,外环为电压环、内环为电流环.母线电压环维持直流母线电压保持在设定值.d 轴输入为母线电压设定值与实际值的差值,经过控制器调节后,获得与id相减,经运算可得到ud,解耦运算得到d 轴控制量.q 轴电流参考值=0,与iq相减后,经控制器调节,获得加-ωLid+eq得到.

图2 网侧变流器控制策略图
2 仿真分析
搭建了永磁直驱风力发电系统仿真模型,参数如表1 所示.
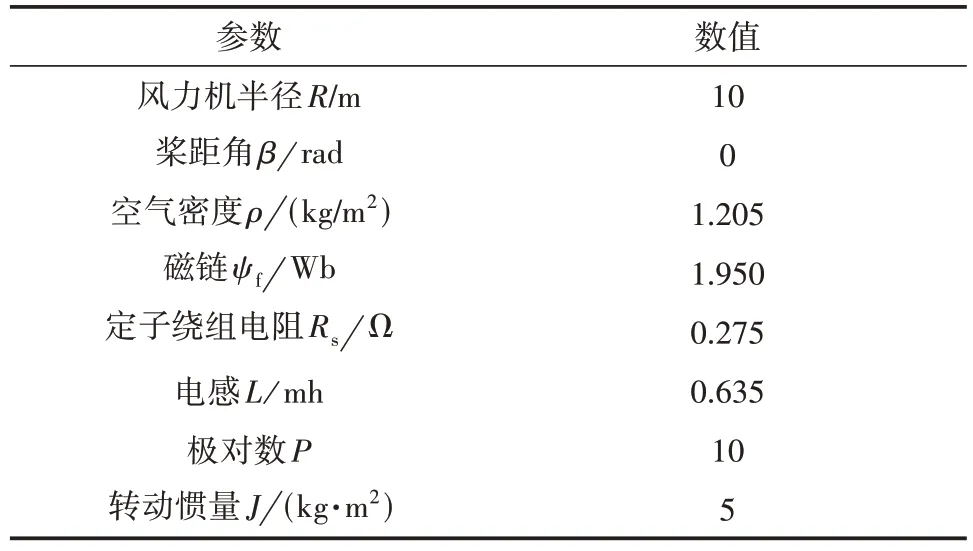
表1 风电系统主要参数
为验证控制策略在多种风速情况下的可行性,风速输入选择稳定风速、渐变风速、阶跃风速相结合方式.设置t=0~1.5 s 时,风速为7 m/s;t=1.5~2.4 s 时,风速从7 m/s 匀速上升到10 m/s;t=3.5 s 时,风速发生阶跃,从10 m/s 下降到8 m/s.仿真波形如图3 所示.

图3 风速图
图4 为非奇异终端滑模控制与自抗扰控制所得功率与风力机预测对比曲线图.由图4 可知,在风机开始运行时,两种控制都能快速反应,但与非奇异终端滑模控制相比,自抗扰控制无超调.当风速逐渐升高时,风机输出功率随风速变化而变化.当达到最大设定风速时,自抗扰控制能紧紧跟随预测功率,在3.5 s 时,风速发生阶跃,从10 m/s 下降至8 m/s 时,自抗扰控制超调量更低且过渡更加平稳.
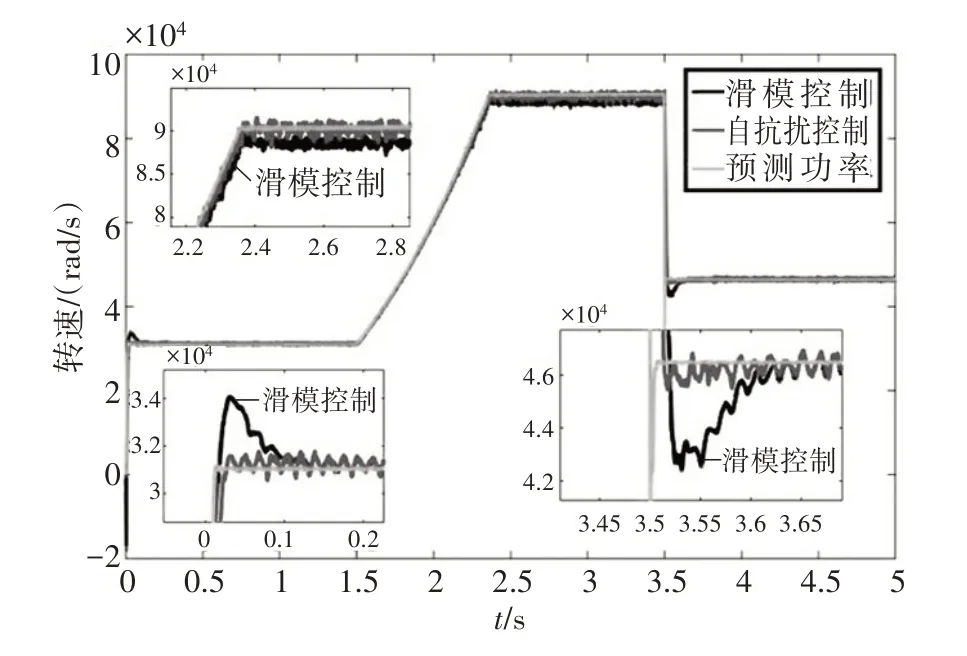
图4 输出功率对比图
图5 为转速对比曲线图.曲线结果表明,在风机开始运行和风速发生阶跃时,两种控制方法下的发电机都能快速达到额定转速,但当达到最大设定风速时,与非奇异滑模控制相比,自抗扰控制下的电机转速与理想转速偏差更小.
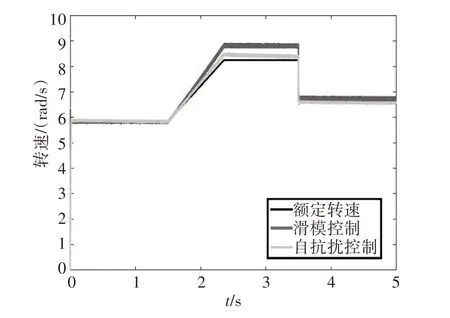
图5 转速跟踪对比图
图6 为得到的直流母线电压对比曲线图.从仿真曲线放大图可以看出,在风速发生阶跃时,直流母线电压发生变化,但自抗扰控制下电压变化超调量更低.

图6 直流母线电压对比图
图7 为得到的机侧iq轴电流对比图曲线.从仿真曲线图可以看出,两种控制方法下的iq轴电流基本相同,在风速达到最大时,自抗扰系统控制下的iq轴电流稍大,同时自抗扰控制下并网功率与预测功率拟合更好.

图7 iq轴电流对比图
3 结论
针对双PWM 变流器的永磁直驱式风力发电系统,设计了滑模控制方法与自抗扰控制方法,并在此基础上通过稳定风速、渐变风速、阶跃风速响应实验,全面比较了ADRC 与带趋近律的SMC 控制器两种方法的有效性、抗干扰能力和鲁棒性.仿真结果表明,两种方法都能有效地控制此风力发电系统,但与带趋近律的SMC 相比,自适应控制器具有更强的抗干扰能力和鲁棒性.
