具有年龄结构的三种群捕食与被捕食系统的最优生育率控制

周子娟

(兰州交通大学 数理学院,甘肃 兰州 730070)

有关生物种群系统的问题自提出以来,便一直被广泛讨论,对于具有年龄结构的最优控制问题前人已做了大量研究[1-5]。种群中新生个体的出生率对整个种群的延续有着至关重要的影响,研究种群生育率能使系统种群密度尽可能接近理想分布,近年来已有许多学者对该问题做了研究[6-9]。文献[10]研究了基于时滞的单种群模型的最优生育率控制;文献[11]讨论了周期问题下单种群模型的最优生育率控制问题;文献[12]对具有竞争关系的两种群系统的最优生育率控制问题做了研究。上述研究并未深入考虑多种群间的相互作用关系(例如食物链关系等),而大型生态系统中的一个重要组成部分是三种群捕食与被捕食系统。因此,本文在上述研究基础上,考察一类具有年龄结构的多种群模型的最优生育率控制问题,该系统由三个相互作用的食物链种群构成,研究其生育率控制问题更具现实意义。

1 模型建立

考虑模型

(1)

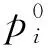
设所期望系统(1)的理想状态为zid(a,t)∈L2(Q),因此,通过选取适当的控制量βi(a,t),使得种群的密度pi(a,t;βi)尽可能地逼近zid(a,t),同时βi(a,t)也尽可能小,来达到目的。考虑最优控制问题

(2)

其中,pi(βi)是系统(1)相应于βi=βi(a,t)的解。允许控制集为

Ui={βi∈L∞(Q):0<βi(a,t)<1,∀a∈(0,A)},i=1,2,3;U=U1×U2×U3。

基本假设如下:

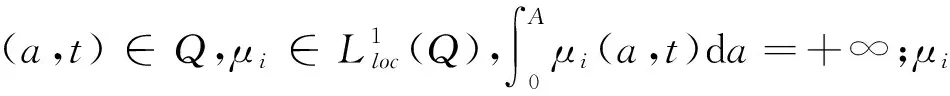
(H2)λi∈L∞(Q),0≤λi≤C2,这里C2是正常数。

(H4)0≤β0≤βi(t)≤β0,对∀t>0,β0和β0都是正常数。

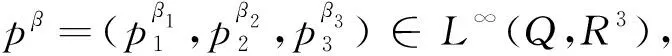
2 最优生育率控制的存在性

构造极值化序列并利用Mazur定理给出最优控制问题(1)的存在性结论。

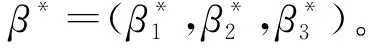
证明设

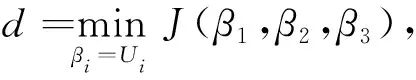
(3)

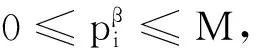
(4)

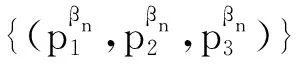
(5)

在L∞(Q)上成立。由文献[14]中引理5.1.1有

(6)

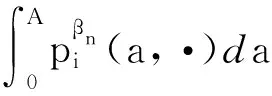
(7)

因Ui(i=1,2,3)有界,则U1×U2×U3中存在子序列,仍记为{(β1n,β2n,β3n)},当n→+∞时

(8)

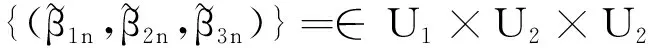
(9)

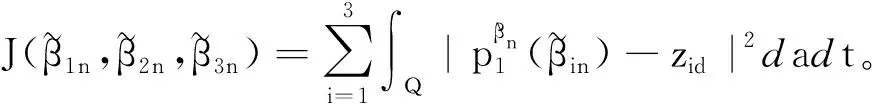
(10)

令式(10)中n→+∞,再由式(3)得到

(11)

故显然有

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

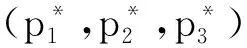
3 必要性条件

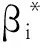
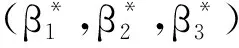
(20)

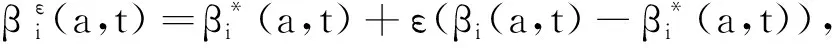
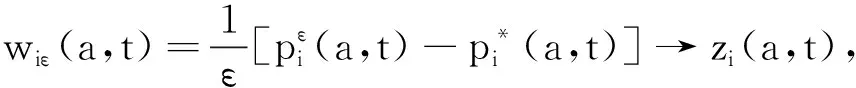
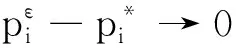
wiε→0。

(21)

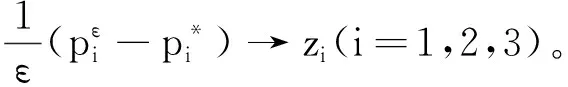
故引理1得证。

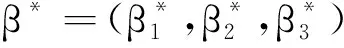
(22)

其中qi=(q1,q2,q3)是下述共轭系统的解:

(23)

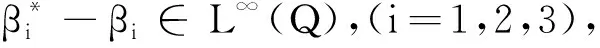
整理可得

(24)

由引理1,对式(24)取ε→0+时的极限,得到

(25)

对式(23)第1式两边同乘以z1(a,t)并在Q上积分,得到

(26)

又有

(27)

在式(27)的推导过程中,利用了q1(A,t)=q1(a,T)=0。将式(27)代入式(26),那么

再由式(20)第1、2、3式整理得到

(28)

(29)

(30)

结合式(28)～(30),有

4 结论

考虑到生育率对生物种群繁衍的影响,本文在假设条件下,建立一类具有年龄结构的三维食物链系统,分析了模型的最优生育率控制问题。利用极值化序列和Mazur定理证明了该模型最优控制的存在性,说明研究该系统的最优控制是有意义的,随后借助法锥概念得到了最优生育率控制的必要条件。种群的发展一般还会受到种群规模制约,因此建立更加完善的食物链模型更具现实意义。在之后的研究中,可以考虑非线性系统的最优生育率控制问题。