基于VIKOR方法的通用机场选址决策
2024-01-30陈吉星张龙妹房泓言
赵 龙,陈吉星,张龙妹,万 宇,房泓言,李 权
(1.沈阳航空航天大学 民用航空学院,辽宁 沈阳 110136;2.中国民用航空飞行学院 机场学院,四川 广汉 618307)
0 引言
选址作为整个通用机场工程建设中的重要组成部分,选址方案的准确性和科学性在很大程度上决定了通用机场未来的发展空间和运营效果[1-2]。机场的建设是一个需经过大量考察和决策的复杂过程,其涉及的因素包括地理位置、地形地貌、净空条件和空域限制、工程和水文地质等多个方面[3]。机场建设需要进行可行性和必要性分析,并通过初选、预选和比选等环节,综合考虑场址的多种因素,最终确定首选场址。因此科学定量地确定通用机场的场址具有重要的研究意义。
目前,史跃亚采用细化分层、隶属度函数分析和组合权重等方法,构建了一种新型机场选址评价模型,并在成都第二机场选址成功验证了其可靠性和准确性[4]。朱来辉等采用模糊层次分析法(FAHP)以及空间分析技术提升了模型的准确性,使模型更加贴近现实情况[5]。郝铭佟等建立了一个包含三级指标的树型层次结构,将指标量化,为通用机场选址方案评价提供了基础[6]。李琪佳等借助ArcGIS软件得出气象因素的分级图层,使用秩序质心法计算权重,得出适宜性指数图,并筛选出适宜的备选场址[7]。Sennaroglu等采用多准则决策方法,用层次分析法(AHP)确定权重,使用PROMETHEE和直觉模糊多属性决策(VIKOR)方法对四种备选方案进行排名和选择[8]。Kiani等针对伊朗德黑兰省机场定位问题进行了研究,采用优先排序技术(TOPSIS)方法处理多重标准和整合层数的问题,用加权叠加方法确定标准的权重,并获得了科学可靠的定位方案,具有实际应用价值,为航空行业领域做出了积极贡献[9]。Erkan等研究在利比亚使用AHP和秩序质心(ROC)两种方法来确定最佳机场位置,以改善该地区的经济和交通情况,并通过敏感性分析评估方法的可靠性,为利比亚及其他国家的机场选址提供了实用方法和实质性支持[10]。
针对通用机场选址这一决策问题,以山东某地区为实例,通过对通用机场选址的研究,确定了影响决策的9个因素,采用科学性、客观性和有效性的坎蒂雷赋权法和VIKOR决策方法,借助Matlab算法程序建模解算,对可能的选址方案进行排序,最终得出最佳的通用机场选址方案,并对该方法进行了灵敏度分析。
1 决策模型原理
VIKOR与TOPSIS方法都常用于解决多属性决策问题,但在细节上不同:VIKOR方法相比TOPSIS方法多了一个决策机制系数,可以使决策者做出更激进或更保守的决策。在VIKOR方法中,决策者可以根据自身需求确定各指标的重要性,从而更全面地考虑不同指标之间的权衡和优先级[11],最终得到带有优先级的折中方案,可明显看到通过VIKOR排序后的最佳方案和与其他方案的差距。
对于通用机场选址这一多准则决策问题,有多种因素对其产生影响,选取以下9个作为考虑的因素:与主服务城市发展规划符合度、交通情况、电磁环境条件、净空条件、工程地质条件、供水供电供气条件、通信条件以及与邻近机场关系、工程经济量[2]。因此,在通用机场选址研究中使用坎蒂雷赋权法确定9个因素决策指标的权重,利用VIKOR方法进行多属性选址决策。
1.1 坎蒂雷赋权法原理
坎蒂雷客观赋权方法适用于指标间相互关联的决策问题,在实际的评价决策中,一般情况下各要素之间都存在一定的关联性,具有广泛的适用性[12]。认为衡量指标与综合指标之间相关性的相关系数与该指标权重应该成比例,权重高低应由指标与综合指标之间的相关程度来确定,采用
计算。具体来说,指标Xi和其权重Wi应当与综合指标的相关系数cor(Xi,Y)成比例,即Wi∝cor(Xi,Y)。
因此,与综合指标高度相关的指标应赋予较大的权重,反之则赋予较小的权重[13]。方法通过计算原始数据的相关系数矩阵R来分析不同指标间的相互影响性,即R=Ri(j)是i指标和j指标数据的相关系数。计算标准差对角矩阵S来分析同一指标下不同评价对象之间的变异性,即
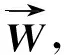
经过归一化处理后可得到各指标的权重。
在进行坎蒂雷赋权前需要对决策矩阵做标准化处理,为了减少和消除不同的指标对量纲的干扰,这里采用线性比例变换法。
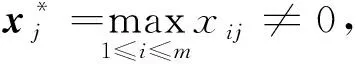
1.2 VIKOR决策原理
VIKOR决策方法是一种多准则妥协解排序方法,采用最大化群效用和最小化个体遗憾值的折中排序能够得到决策者容易接受的妥协解方案。
VIKOR决策方法的基本思想是:确定正理想解(PIS)和负理想解(NIS),然后根据待选方案与理想指标值的距离,以折中妥协的方式进行排序[14]。其中,正理想解是所有评价准则中的最优值,而负理想解则是所有评价准则中的最差值。通过最大化群体效益和最小化个体损失,得到各属性之间的平衡点,从而得到更为准确的综合评价[15]。计算步骤如下。
(1)
式中:fij为第j个评价事物在第i个指标上的标准值。
步骤2 群体效益值Si、个体遗憾值Ri的确定:
(2)
式中:Xij表示方案j在第i个指标上的指标值。
步骤3 VIKOR指数的Qi计算公式:
(3)
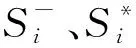
2 实例模型构建
选取山东某地区为参考实例,通过对通用机场选址的研究,确定影响决策的9个因素,进行坎蒂雷赋权后运用VIKOR法,从3个备选场址中得出最优选择,并得出3个场址综合决策排序分析。经过构建,通用机场选址方案评价指标体系如图1所示,其中包括多个维度的指标,如运行条件、机场自然和技术条件、公共设施条件和经济条件等指标,这些指标能够全面反映通用机场的关键属性和条件,从而进行全面、准确的选址决策。
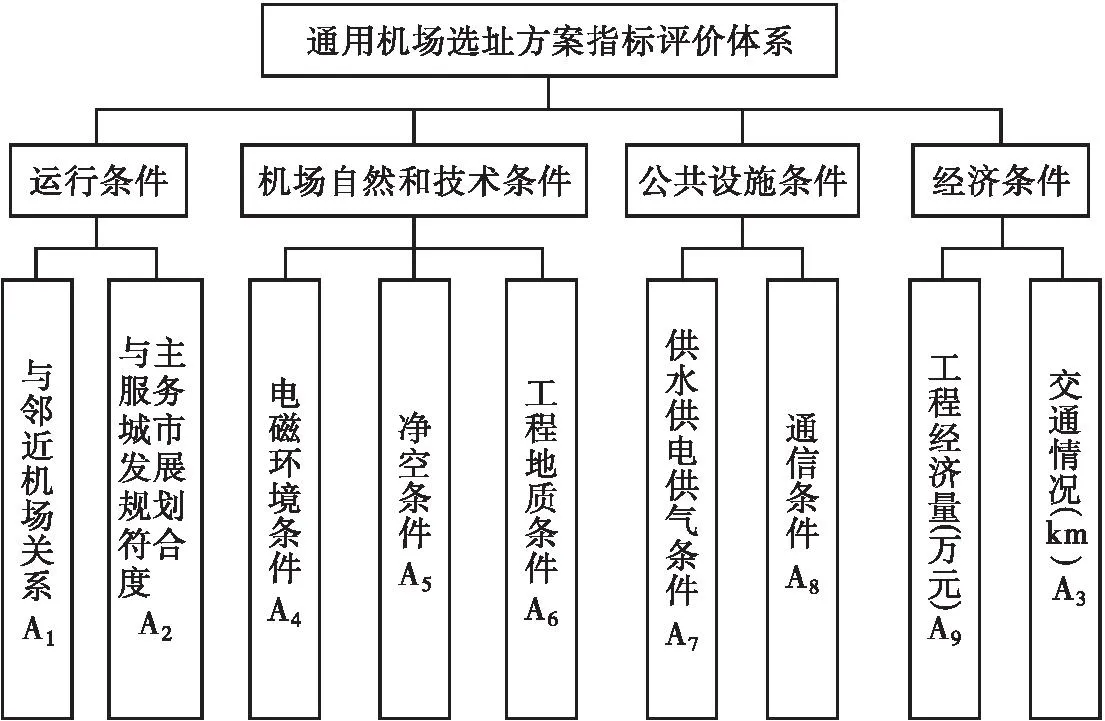
图1 通用机场选址决策方案指标评价体系
选取的目标通用机场建设项目选址涉及3个可选场址,从中决策出首选场址,各指标数据来源于公开文件《山东某地区通用机场建设项目建设用地规划》,如表 1所示。
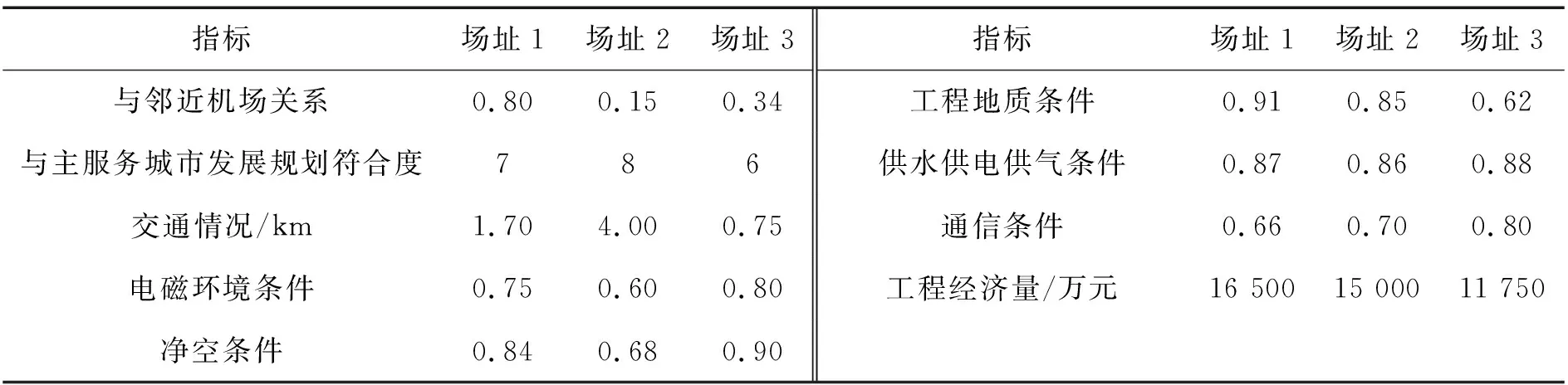
表1 机场选址原始指标数据
2.1 决策指标的标准化
为了消除指标之间可能存在的量纲影响,采用线性比例变换的方法对矩阵进行标准化处理,得到标准化矩阵X′。这种处理方法可以使不同指标在综合评价时具有相同的权重,从而能够得到更为准确的评价结果。
2.2 坎蒂雷赋权法确定指标权重
步骤1 使用Matlab软件程序计算出标准化矩阵X′的标准差对角矩阵S=diag(0.6965,1,-3.851 086 11)。
步骤2 综合考虑相关性和变异性两种因素,得到乘积矩阵
解算出矩阵RS的最大特征值对应的最大特征向量后,可以得到评价指标的权重W,其中,A1为0.0290,A2为0.2010,A3为0.6889,A4为0.1864,A5为0.1863,A6为0.2481,A7为0.1830,A8为0.1268,A9为0.2161。
2.3 VIKOR实例选址决策
步骤1 节点综合权重的计算,根据式(1)可得指标正理想解为1.1126和负理想解0.2785。
步骤2 根据式(2)计算出群体效益值、个体遗憾值。各场址的Si依次为0.6965,1.0000,0.3851。各场址的Ri依次为0.5545,0.7640,0.0930。
步骤3 根据式(3)得到VIKOR决策指数Q1=0.6921,Q2=1.0000,Q3=0。3个备选场址的群体效益值、个体遗憾值和最终决策指数如图2所示,易见场址间差距。其中Q3 图2 决策结果图 灵敏度分析是一种常用的决策分析方法,它可以通过对决策参数的微小波动进行分析,来评估它们对评估结果的影响程度。这种方法能够帮助决策者更好地了解决策参数的重要性,从而优化决策方案,当评价方法中的指标权重对评价结果的影响较小时,表明该方法具有较高的稳定性和鲁棒性[16]。 针对评价结果的指标权重变化率进行分析,并利用基于坎蒂雷赋权的VIKOR决策法,对比不同权重变化率下节点重要度的排序如图3所示。结果表明,在一定范围内的权重变化下,节点重要度顺序保持不变,因此该方法具有很好的鲁棒性。 图3 坎蒂雷赋权的VIKOR评价结果灵敏度分析 针对通用机场选址这一决策问题,提出一种将坎蒂雷赋权法和VIKOR方法相结合的通用机场选址决策方法。以山东某地区为实例,采用科学性、客观性和有效性的坎蒂雷赋权法建立并确定指标体系和权重,利用通用机场选址模型和原理,借助Matlab算法程序进行建模解算。结果表明,基于坎蒂雷赋权的VIKOR决策法的解算得出了最优选址方案,并且结果稳定,鲁棒性更好,决策者根据自身需求确定其重要性,不仅能得到唯一最优解,还可以得到带有优先级的折中方案,同时能够处理多个准则和不同类型的数据。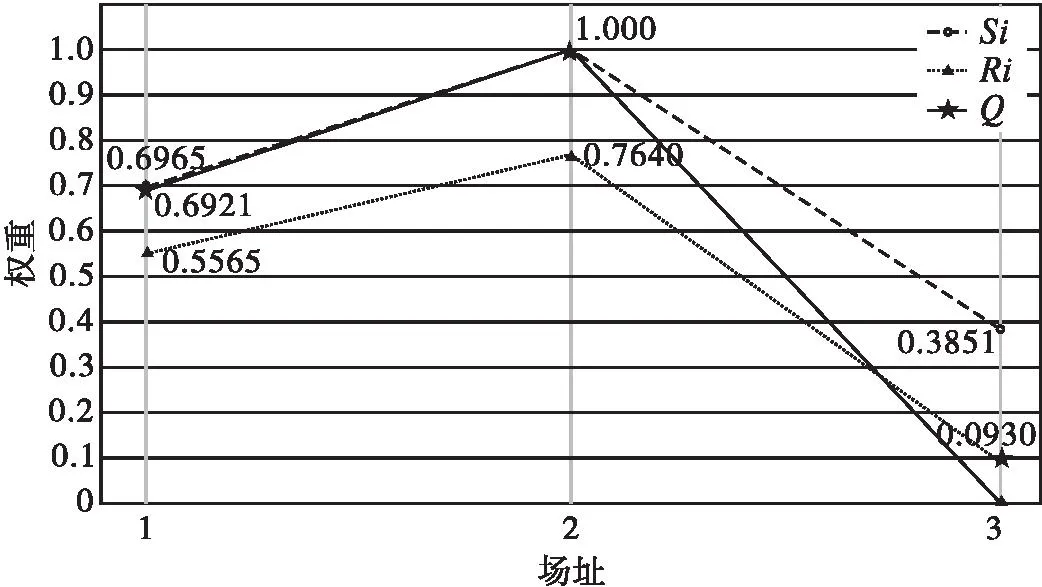
3 评价结果灵敏度分析
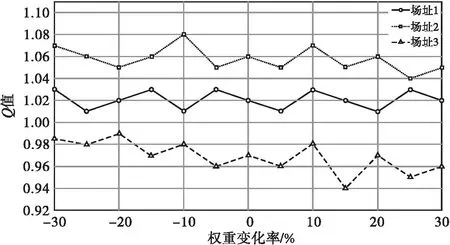
4 结论
