基于改进SCS-CN 模型的降水径流预测

王婉婉 周 超 杜富慧 王振龙

（1河北工程大学，河北邯郸 056021；2安徽省（水利部淮委）水利科学研究院五道沟水文实验站，安徽蚌埠 233000）

地表径流作为水文循环的关键部分，是集雨灌溉的主要来源[1-2]，但其会加剧土壤侵蚀、水源污染、洪涝灾害以及养分流失等[3-4]，开展径流水文模拟研究，是进行产流预报、土壤侵蚀预报的重要基础。预测地表径流的关键在于建立方便有效的产流模型，现行地表径流模拟方法众多，如Philip 模型、Green-Ampt 模型和Horton 模型等[5]，以上模型存在输入参数多、计算复杂等短板，在实际应用中受到限制[6]。近年来，径流曲线SCS-CN模型[7]不断得到更新和修正[8]，其优点在于结构简单，参数获取方便，为水土保持工作提供了重要的科学依据，成为广泛使用的水文模型之一[9]。由SCS 建模原理可知，使用该模型的关键点在于参数CN和S的确定，基于此，根据不同研究区实测土壤特征、水文情况等对SCS-CN模型的CN进行了修正。Mishra等[10]将CN值与土壤湿度条件的变化趋势作为考虑因素进行研究，建立了CN值与前5 天降水量之间的幂函数关系，以避免在确定初始土壤含水量过程中AMC条件的等级发生突变。在对SCS-CN模型进行修订及土壤水分核算程序的构建基础上，Singh等[11]构建了对初始土壤含水量的间接估算公式的精简SCS-CN模型。以上均是单独考虑降水量、初始土壤水分来对SCS-CN模型中的CN值进行修订，而将二者结合对模型中的CN值进行改进的研究较少。基于此，本文利用淮北平原五道沟实验站1972—2021 年降水径流106 场次实验流域实测资料，基于降水量以及前期影响雨量修正CN值对SCS-CN模型进行改进，并对其结果进行可靠性验证，为今后更深入地探讨该地区地表径流模型的应用及改进提供参考。

1 材料与方法

1.1 实验区概况

五道沟水文实验站是淮北平原区大型综合实验站。该地区（117°21'E，33°09'N）位于安徽蚌埠北25 km处的新马桥原种场境内，占地面积1.4×104m2，属于平原区封闭式小流域实验站[12]。该实验站位于淮北平原南部，处于我国南北气候分界带，属于半干旱半湿润季风气候区，四季分明，冬季干旱少雨，夏季炎热多雨[13]，站内土壤以砂姜黑土为主。1972—2021年，五道沟地区多年平均降水量为903.32 mm，其中2013 年降水量最大，为1 416.2 mm，1978 年降水量最小，为410.3 mm，汛期为556.6 mm，非汛期为335.4 mm；多年平均径流深126.6 mm，1991 年径流深最大，为522.4 mm。该区域地下水埋深1～4 m，年变幅1～3 m，属地下水浅埋区。站内设有相嵌套的1.36、6.00 和1.20 km2闭合实验流域，积累了1953—2021 年降水产流实测资料。站内设有水文气象全要素观测场、62套非称质量式蒸渗仪及大型野外人工降水实验设备等，积累了长系列气象全要素观测资料。

1.2 研究方法

1.2.1 模型原理SCS-CN模型假设流域内实际径流量与可能最大径流量的比值等于实际入渗量（F）和流域潜在最大入渗量（S），初损量与潜在最大入渗量成正比，即式（1—2）。

式（1—2）中，Q为径流深，单位mm；P为降水量，单位mm；Ia为初损量，单位mm；S为潜在最大入渗量，单位mm；λ为初损率，标准SCS模型定义λ= 0.2。

潜在最大入渗量由式（3）确定。

式（3）中，CN为径流曲线数。

CN的标准值与流域前期土壤湿润程度（AMC）、坡度、植被、土壤类型和土地利用状况有关。当降水量和径流量已知时，可由式（1—2）反推得到式（4）[14]。

在实际应用中，参考某农业用地CN值表，确定本文所用的标准SCS-CN模型AMCⅡ状态下的CN值表[15]，如表1所示。

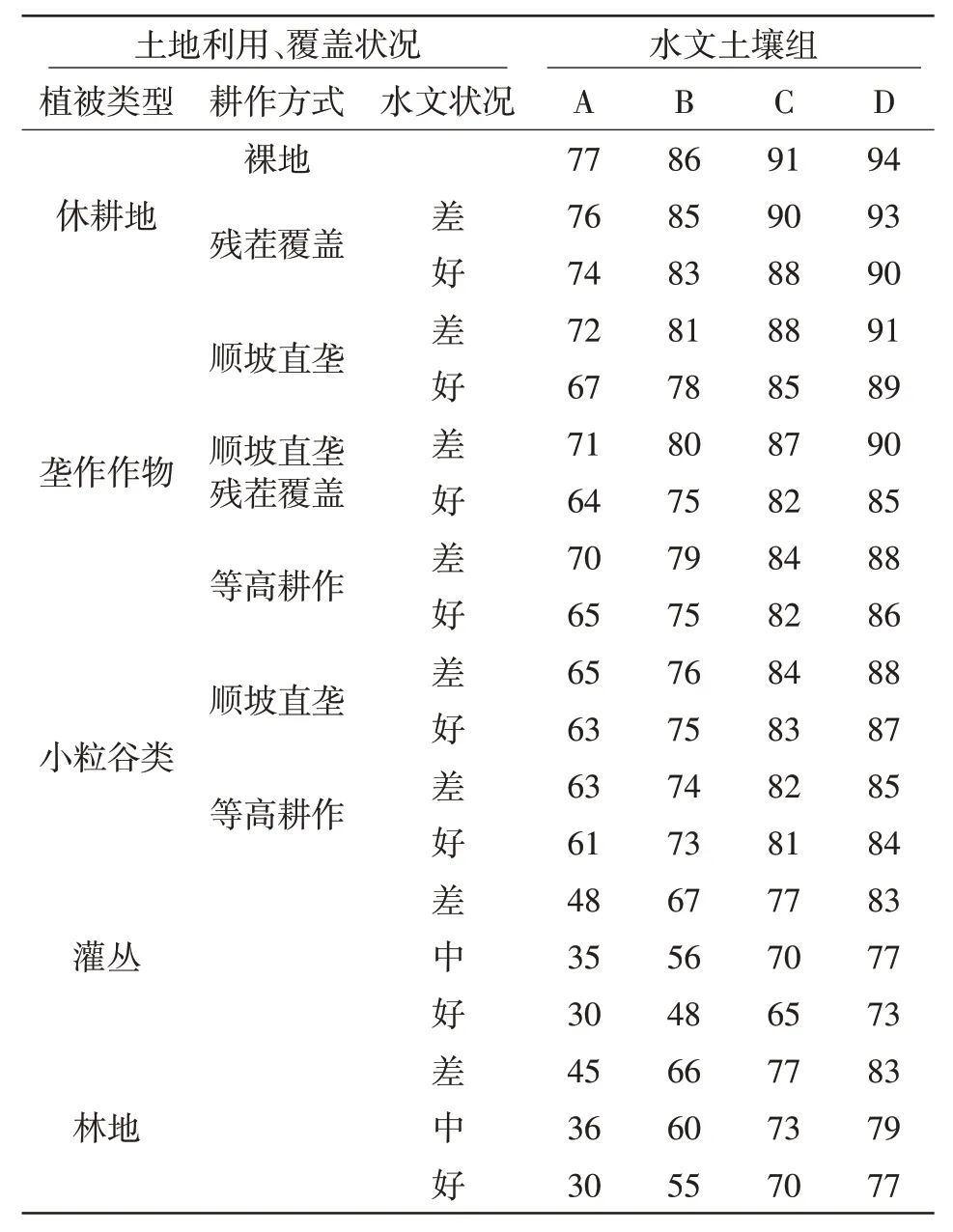
表1 在AMCⅡ下不同土地利用方式及覆盖状况下的初始CN值

根据表2，将土壤湿润程度按降水发生前5日降水总量划分为干旱（AMCⅠ）、正常（AMCⅡ）和湿润（AMCⅢ）3 种状态，根据CNⅡ值计算其他两种状态下的CN值[16]，如式（5—6）。

表2 前期土壤湿润程度等级划分单位：mm

式（5—6）中，CNⅠ、CNⅡ和CNⅢ分别代表干旱、正常和湿润状态下的CN值。

1.2.2 模型评价标准模型模拟效果采用模型效率系数E度量计算结果与实际测量数据的匹配程度，这一系数揭示了二者1∶1 直线的接近程度，E值越接近1，表示模型有效性越好；相关系数R2可以反映计算值与实测值之间的相关程度，其值越接近1，表示接近程度越高；采用相对误差RE来反映预测值偏离实际值的程度，RE值越小，表明预测值精确度越高。

2 结果与分析

2.1 标准SCS模型CN值确定

在标准SCS-CN方法中，CN值由水文条件以及土地覆盖类型等因素决定[17]，确定过程分为以下3个步骤[18]。一是确定土壤的水文土壤组。二是构建CN值表[19]，初步获取CN值，综合其水文情况、土壤特征等因素，使用交叉表原理进行检索和匹配，以初步确定每个离散单元的CN值，具体分类见表2。三是确定CN值，通过交叉查表得到的CN值为CNⅡ，在实际情况下，以CNⅡ为基础，通过式（5—6）推算出CNⅠ和CNⅢ。研究区分布广泛的土壤为砂姜黑土，占全区土壤面积的54%，根据其土质分布以及土地利用类型和水文条件确定研究区CNⅡ=64，经公式（5—6）换算得出CNⅠ=44、CNⅢ=81。

2.2 参数敏感性分析

2.2.1 初损率λ对地表径流的影响设定CN=44，P=97.2 mm，λ取值0.2，且变化范围为0～0.2，从第1步到第10步，以每减少20%步长为基准调整初损率λ，观察地表径流Q的相对变化，初损率λ对地表径流的影响关系见图1。由图1可知，在一定的降水量P和CN值条件下，随着初损率λ的增加，预测地表径流量呈现逐渐减小的趋势，在初损率λ以20%为步长从0.2 减小到0 的过程中，预测径流分别增加0.88%、2.00%、3.33%、4.86%以及6.55%。结果表明，当降水量P以及CN值为定值时，研究区的预测地表径流对初损率λ有一定敏感度。

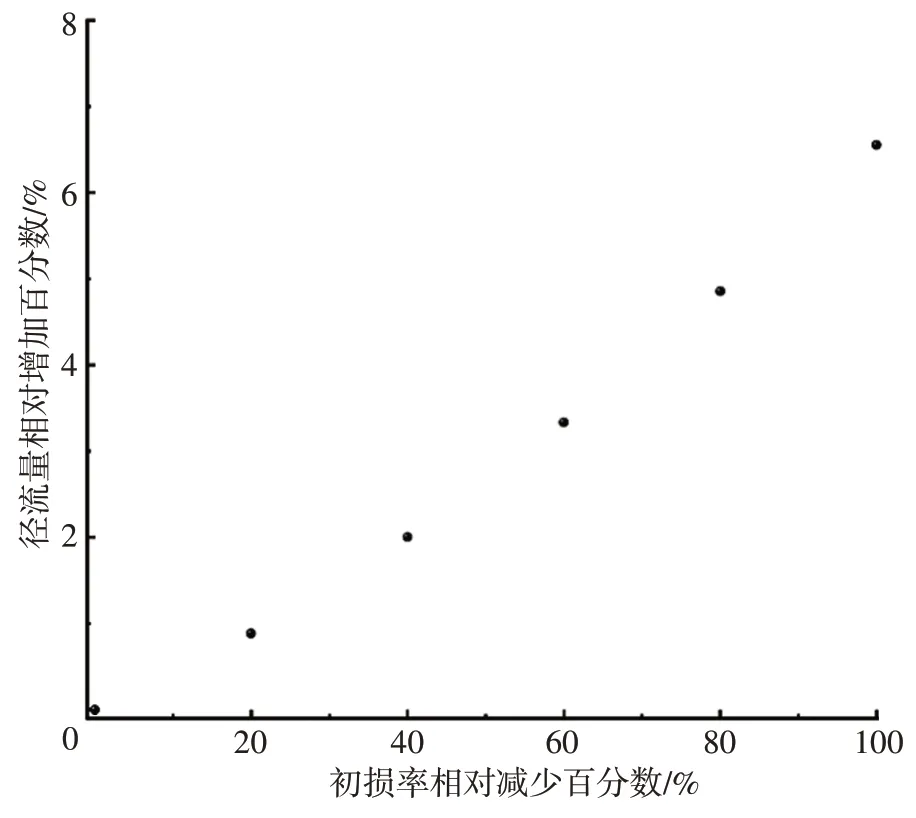
图1 初损率λ对地表径流的影响

2.2.2CN对地表径流的影响设定降水量P=34.8 mm，λ=0.2，在此前提下，使初始值为44，后续以10%为基准逐步增加的方式调整CN值，并观察地表径流Q的相对变化率，了解CN值对地表径流Q的实际影响（图2）。由图2 可知，当降水量P和初损率λ一定时，地表径流Q和CN值的关系在CN相对增加百分数为0～40%的范围内呈负相关，而在增加百分数为40%～100%的范围内呈正相关且变化曲线越来越陡。当CN值从0增加到60%时，预测地表径流的最大增加百分数为0；当CN值从60%增加到100%时，预测地表径流的增加百分数最大为3.09%。结果表明，当降水量P和初损率λ一定时，CN值越大，对径流预测结果的影响越大。

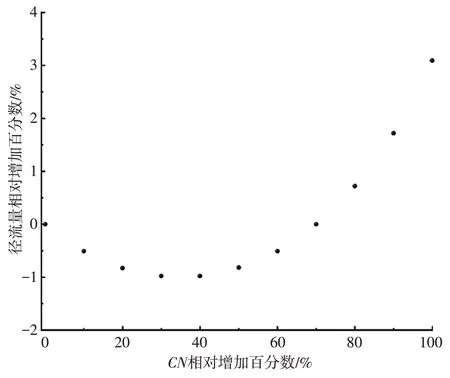
图2 CN对地表径流的影响

2.2.3CN和降水量对初损率λ相对敏感性的影响基于初损率λ随CN值和降水量变化的相对敏感性，对降水量P或径流曲线数CN的值进行调整，得到初损率λ 的相对敏感系数Sr。在计算过程中，结果可以为正，也可以为负，主要关注Sr的绝对值，绝对值越大，模型输出变量对发生改变的参数越敏感。计算过程如式（7）[20]。

式（7）中，a代表初损率λ 的初始值，取值0.2；b代表计算地表径流，单位mm；a1、a2代表初始初损率λ±10%对应的初损系数值，分别为0.18、0.22；b1、b2代表初始初损率λ±10%对应的计算地表径流量，单位mm。

2.2.4CN对初损率λ相对敏感性的影响设定降水量为定值，CN值以步长为5 的条件在[65，100]范围内增加。用相关公式计算出相应的地表径流量，根据式（7）计算初损率λ的相对敏感系数Sr，λ随CN值变化的相对敏感性见图3。由图3 可知，研究区初损率λ对CN值的相对敏感系数Sr均为负值，此结果说明，随着初损率λ的增大，计算径流量Q呈减小趋势。当CN值在[65，100]范围内变化时，Sr的变化范围为-1.75～0；随着CN值的增大，其绝对值逐渐减小，并无限接近0；当CN值达到一定值时，相对敏感系数Sr几乎不变。结果表明，计算径流量Q随初损率λ的变化趋势是随着λ的增大，Q呈减小趋势；随着CN的增大，Q和λ对CN值的变化敏感性呈降低趋势。

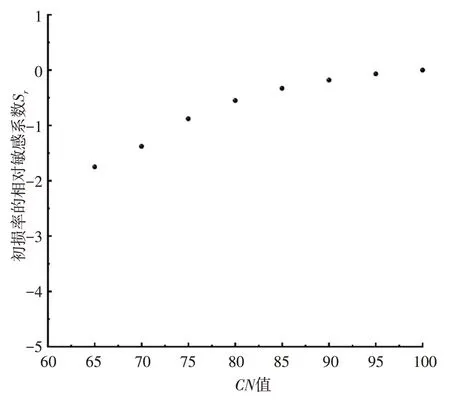
图3 初损系数λ随CN值变化的相对敏感性

2.2.5 降水量对初损率λ相对敏感性的影响由图4 可知，当CN取定值，降水量P在70～200 mm 范围内变动时，初损率λ相对敏感系数Sr的变化范围为-23.74～0。Sr的所有变化值均为负数，随着降水量增加，其绝对值不断减小，并逐渐接近0。当降水量P变动时，随着λ的增大，Q呈减小趋势；随着P的减少，λ对P的敏感度增加，Q和λ对P的影响加大。当Sr的绝对值小于1时，不考虑Q对λ的变化对计算径流量Q的影响。由图4 可知，当降水量为170 mm时，Sr的绝对值小于1，并越来越接近0。综上所述，降水量P越大，初损率λ对降水量P的敏感性越低，初损率λ的取值对计算径流量Q的影响便可以忽略不计。

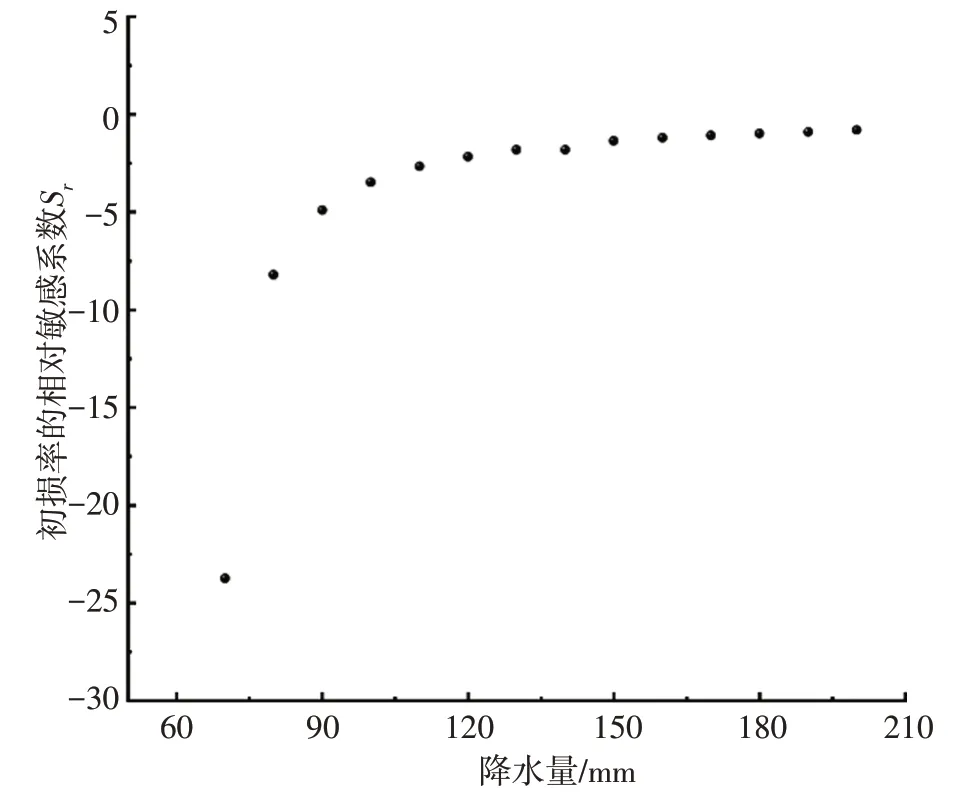
图4 初损系数λ随降水量变化的相对敏感性

2.3 改进SCS模型

2.3.1 建模原理利用1972—2011 年实测场次降水径流数据，由式（4）得到与降水量对应的S值。采用SPSS 27.0 软件分析S值与场次降水量以及前期影响雨量的相关性，若三者相关性显著，则进行回归分析，得到S值随降水量及前期影响雨量变化的关系式，进而根据式（3）计算研究区CN值。S值与降水量及前期影响雨量相关性分析结果见表3。

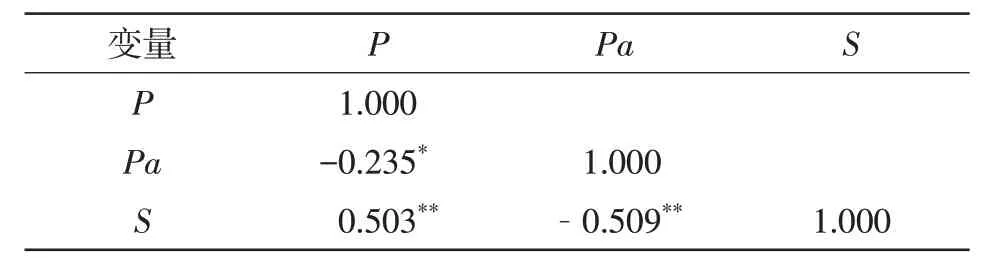
表3 S值与降水量、前期影响雨量相关性分析结果

由表3 可知，降水量与S值极显著相关（P＜0.001），前期影响雨量与S值显著相关（P＜0.05），说明S值分别与降水量和前期影响雨量具有显著相关性。基于此，将实测数据按照地下水埋深分为Ⅰ级（0～0.4 m）、Ⅱ级（0.4～0.8 m）、Ⅲ级（0.8～1.2 m）、Ⅳ级（＞1.2 m）4个级别，在不同地下水埋深级别下分别对S值、降水量和前期影响雨量做变量回归分析。S随降水量和前期影响雨量的变化回归方程如式（8—11）。

2.3.2 公式验证利用研究区实测的2012—2021 年径流资料对改进公式（8—11）进行验证，验证结果见表4，表4中的计算S值由式（4）计算所得，改进S值由式（8—11）计算所得。由表4 可知，计算S值与改进S值的相对误差绝对值最大为3.1%，平均相对误差绝对值为1.3%，总体相对误差较小，由此可推导S值的改进公式效果较好。

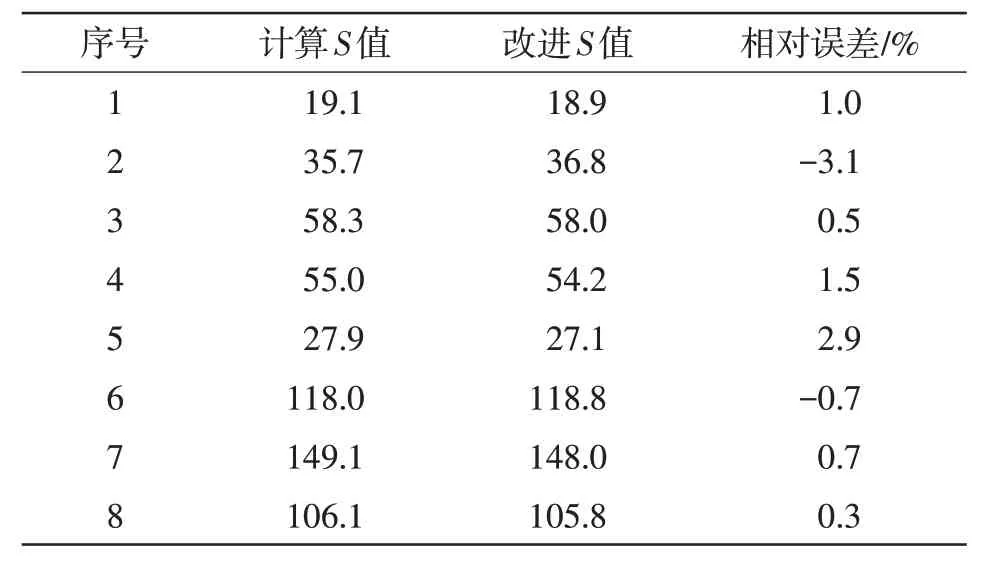
表4 改进公式计算S值验证结果

综上，利用式（4）和式（8—11），根据不同地下水埋深级别的不同，计算不同场次降水量实际CN值，并求出CN值的平均数，得到最终CN值。

2.3.3 模型验证与评价为验证引入降水量和前期影响雨量改进后的SCS-CN模型对研究区径流预测效果，根据研究区径流实验场2010—2021年24场实测径流数据，对改进模型及传统SCS-CN模型的预测效果进行对比验证。在模型验证过程中，利用选取的实测降水径流数据预测，结合各降水场次对应的计算径流深和实测径流深数据点分布的均匀程度及数据回归直线径流1∶1直线的接近程度进行综合分析。

由图5可知，传统SCS-CN模型预测结果与实际径流结果接近率较小，预测径流深结果数据点分布较分散，虽然R2=0.782，但是模型效率系数仅为0.23，单个数据计算和实际数据点的最大偏差情况达863.70%，模型总体平均相对误差达366.67%，远超模型许可误差可接受范围，所以传统SCS-CN模型并不适用于研究区径流预测。

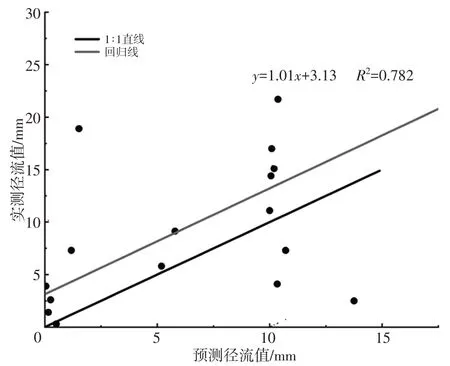
图5 研究区传统SCS-CN模型径流量预测对比

由图6 可知，改进后模型的径流深数据点分布更加均匀，基本均匀围绕在1∶1直线的两侧，径流数据点的相关系数R2=0.864，E=0.78，单个数据最大偏差程度为63.70%，模型总体的平均相对误差为26.67%，改进后模型评价指标均高于标准SCS-CN模型。由此可知，改进后的SCS-CN模型更适用于研究区的径流预测。

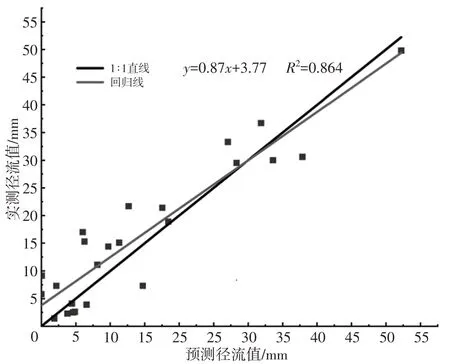
图6 研究区改进SCS-CN模型径流量预测对比

3 结论与讨论

（1）在降水量P和CN值为定值时，随着初损率λ的增加，预测地表径流量呈逐渐减小的趋势；当降水量P和初损率λ一定时，地表径流Q和CN值的关系在CN值相对增加百分数为0～40%范围内呈负相关，而在增加百分数为40%～100%范围内呈正相关且变化曲线越来越陡。

（2）研究区下垫面的初损率λ对CN值的相对敏感系数Sr均为负值。当CN在[65，100]范围内变化时，Sr的变化范围为-1.75～0，在此范围内，随着CN值的增大，其绝对值逐渐减小，并无限接近0，当CN值达到一定值时，相对敏感系数Sr几乎不变；降水量越大，初损率λ对降水量的敏感性越低，初损率λ的取值对计算径流结果的影响便可以忽略不计。

（3）引入降水量以及前期影响雨量对SCS-CN模型进行改进，得出式（8—11）4个公式修正CN值，在此基础上对模型改进。利用2010—2021 年24 场实测降水径流资料对传统SCS-CN模型和改进模型的预测径流效果进行分析验证。标准SCS-CN模型的径流模拟效果不够理想，虽然R2=0.782，但E仅为0.230，模型总体平均相对误差为366.67%，改进模型R2=0.864，E=0.780，模型总体平均相对误差为26.67%，改进后模型评价指标均高于标准SCSCN模型，改进SCS-CN模型对研究区的径流预测更具有适用性。

本文用查表法确定CN值时，运用了土壤前期湿润度的等级标准来进行划分，没有根据研究区实际的本土特征进行验证，对于后面模型的预测精度会产生一定影响，该等级标准对研究区的适用性有待进一步研究，在后续研究中可继续深化。