机器学习在人工增雨效果统计检验中的应用

李 丹 林 文* 刘 群 冯宏芳 胡淑萍 汪智海

1)(福建省气象科学研究所, 福州 350001) 2)(福建省灾害天气重点实验室, 福州 350001) 3)(中国气象局海峡灾害天气重点开放实验室, 福州 350001) 4)(闽南师范大学数学与统计学院, 漳州 363000) 5)(福建省宁德市古田县气象局, 宁德 352000)

引 言

近年人工影响天气事业不断发展,在农业抗旱、水库蓄水、净化空气等工作中发挥了重要作用,作为人工影响天气作业的重要环节,人工增雨作业效果的科学评价受到人们高度关注[1-3]。经过大量实践研究,国内外学者将人工增雨效果检验方法总结为物理检验、数值模拟检验和统计检验[4-15]。物理检验主要针对人工影响天气作业前后云系的宏微观变化特征,结合云降水形成及其催化原理,对比目标云系被影响后产生的相关物理响应(微物理结构或宏观动力结构变化等),对作业产生的直接效果进行定性或定量分析[16-18];数值模拟检验是利用能够描述云降水微物理过程及人工增雨催化过程的数值模式,通过改变催化条件,定量模拟出人工增雨作业后的云系发展变化和产生降水情况,并与未催化的自然发展云系观测结果进行对比,得到作业效果[19-21];统计检验是对间接效果即产生的地面降水进行定量分析,主要通过不同人工增雨试验方案,利用数理统计理论对作业效果进行定量检验分析[22-25]。研究表明,序列分析、双比分析、区域对比分析、区域历史回归分析和基于聚类统计的浮动对比区等方法是常用的统计检验方法。其中,区域历史回归分析检验功效高、准确度和灵敏度较好[26-27],是国内外人工影响天气作业效果检验比较推荐的效果检验方法,该方法基于历史降水长序列数据,通过分析目标区和对比区的降水相关性,估算目标区作业期间的自然雨量,并与目标区实际雨量进行比较,得到的差值则视为增雨作业效果。该方法假定作业期间目标区和对比区的雨量相关关系与历史相同天气下两区域雨量相关关系相同,但实际上该假定很难满足,这是因为实际降水自然变率较大,目标区与对比区的关系缺乏稳定性,从而导致评估结果稳定性较差,这也是区域历史回归方案最大的困难[28-29]。如果能够选择恰当的对比区,且样本足够多,该方案的评估功效仍较高。国内外许多抗旱增雨的业务性试验效果评估均采用该方案。此外,房彬等[30-31]和翟羽等[32]等利用聚类分析进一步改进非随机化人工增雨效果区域历史回归方法,将物理协变量作为控制因子和网格插值计算雨量,提出一种新的浮动对比区历史回归统计检验方法(简称CA-FCM方法),并用于河南人工影响天气作业效果分析,结果表明效果评估功效显著提高[32]。随着机器学习在气象领域的不断发展和广泛应用,发现其能够更好地自适应数据变化并提取特征,具有强大的非线性建模能力[33-37]。

为了尽可能客观、定量地检验人工增雨作业效果,本文基于2014年1月—2023年1月福建地区降水数据和作业信息,利用机器学习和多种数学统计方法[38],对比不同回归统计检验方案,旨在进一步优化基于浮动对比区的最佳自然雨量估测模型,为开展区域内人工增雨效果统计检验提供参考。

本文插图中所涉及的国界和行政区域界线基于审图号为GS(2017)3320号标准地图制作,底图无修改。

1 研究区域和数据

本文研究区域为福建省古田人工增雨效果检验随机试验区,覆盖闽北地区古田、屏南、周宁和建瓯等地,其范围为26.1°～27.3°N,118.0°～119.5°E,选取该区域内古田水库流域人工增雨效果检验外场试验作业影响区域为目标区(图1)。效果检验必须准确预计效果出现的区域、时间、量值等[39],因此效果评估前首先需确定效果所在的区域即目标区。

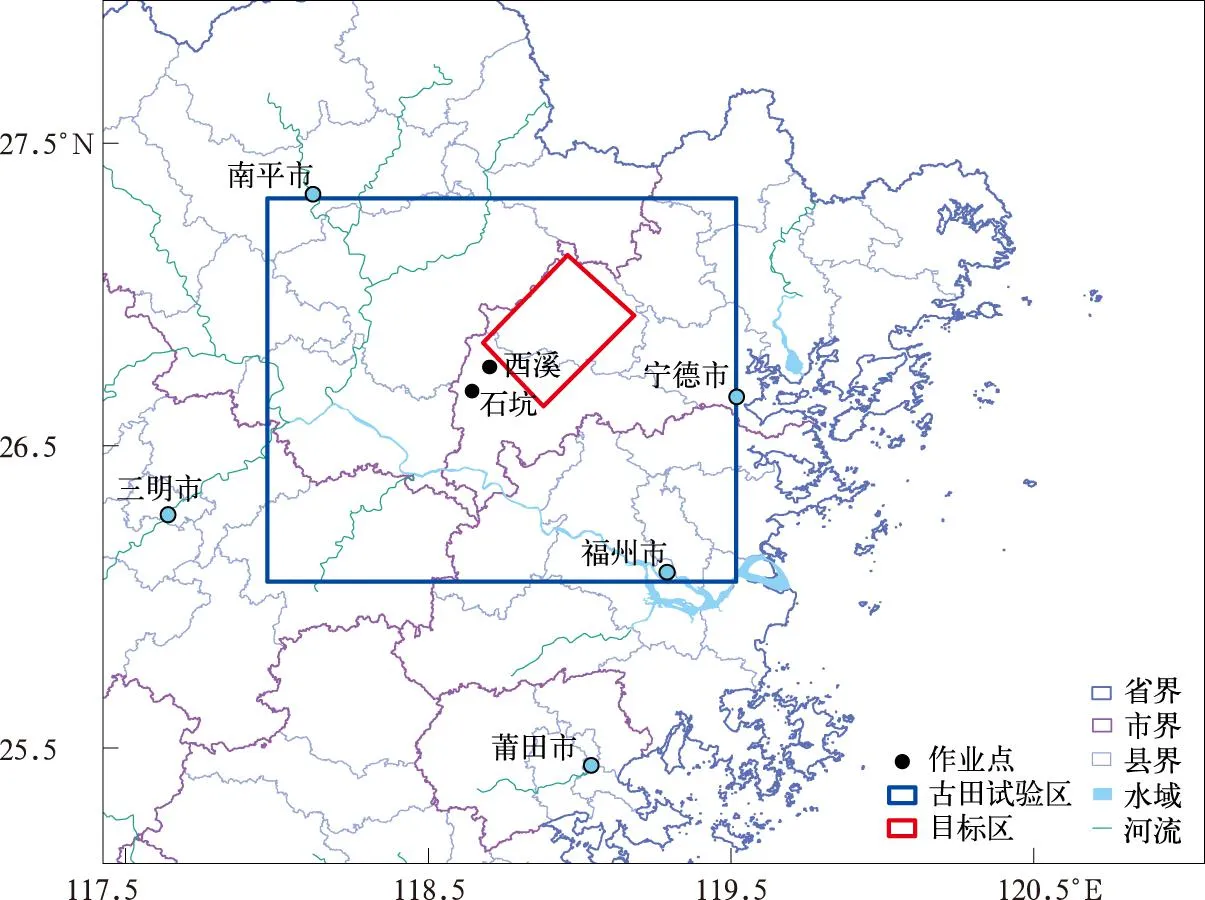
图1 福建省古田人工增雨效果检验基地

本文选取2014年1月—2023年1月试验区自动气象站小时降水数据,结合福建省人工影响天气作业历史数据,根据作业点经纬度、作业起止时间以及目标云系移动范围建立历史数据库并进行标记分类,期间福建省境内共开展人工影响天气作业1.06万余次,试验区内开展人工增雨作业随机试验约80次,其中随机试验主要在石坑和西溪2个作业点进行火箭冷云催化作业。为排除由于人工影响天气作业对自然降水数据的影响,将人工影响天气作业后4 h内目标云系移动过程中覆盖到试验区域的自动气象站降水数据标记为人工增雨作业影响数据库,未覆盖到试验区域的降水数据则标记自然降水数据库,并将试验区域内3个自动气象站雨量不小于0.1 mm的小时降水数据视为1次有效样本,从而保证样本量和数据质量。人工增雨作业信息数据来源于福建省气象局人工影响天气指挥中心。

2 基于区域历史回归方法确定最佳对比区

区域历史回归方案为选择1个或多个与目标区天气地理条件相似、降水相关性较好的区域为对比区,然后根据两区域历史雨量建立区域历史回归方程,将对比区的雨量代入方程求得作业区自然降水估测值,并与作业区降水实测值对比以确定增雨效果。区域历史回归分析要求对比区与目标区相互独立,但天气系统、降水分布和地形等方面的相似度较高,因此本文以降水相似度和地形相似度为主要参数指标。此外,对比区应选择在目标区上风向,确保不受人工影响天气作业催化剂扩散作用的影响。

2.1 主要参数指标

2.1.1 降水相似度

降水相似度决定了对比区与目标区历史自然降水序列关系模型的可解释性,以及基于对比区雨量对目标区自然雨量的可估测能力。虽然用日尺度以上雨量作为统计变量相对简单且方便,但因时间跨度较大,且包含自然降水时段,不利于对影响时间有限的单次人工增雨作业进行合理准确评估。因此选择目标区内各自动气象站小时雨量数据,通过插值获得该区域内小时平均面雨量,表征区域降水强度。

对自动气象站逐时、逐日、逐候雨量进行K-S检验(Kolmogorov-Smirnov test)分析,自然雨量数据集不满足正态分布特征,通过对数变换或者六次方根变换有所改善,不适合直接使用线性关系模型进行两区域数据拟合。刘晴[24]和程鹏等[25]提出为满足统计变量服从正态分布的要求,统计变量相对最优的选择是候雨量或旬雨量的六次方根值。本文对小时雨量进行六次方根变换,采用线性回归分析方法分析目标区和对比区的小时平均面雨量,将二者相关系数作为两区域降水相似度。

2.1.2 地形相似度

地形相似度是基于地图影像数据,利用地形特征数据划分每种地物的分布区域,以区域为基本单位提取影像特征并进行对比。本文综合考虑两个区域地图要素的形状相似、位置相似以及信息内容相似程度,即属性特征相似性。将图片信息转化为数组,通过灰度化处理简化图像色彩,计算所有像素的灰度平均值,通过二值化得到图像的哈希值,比较像素的哈希值差异,利用汉明距离法得到两区域的相似度。

由两区域地形相似度与降水相似度拟合关系可知二者呈较明显正相关关系(图2)。因此,基于自然降水数据库和GIS空间数据,利用浮动对比区方法选取对比区时,将降水相似度和地形相似度较高(面积、形状与目标区相同)的区域确定为最佳对比区。

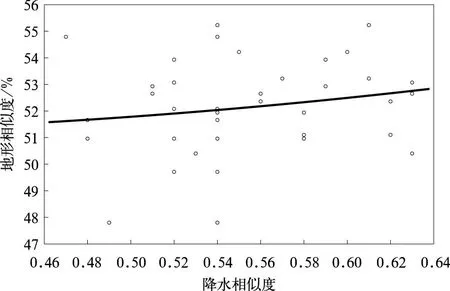
图2 目标区与对比区地形相似度与降水相似度拟合关系

2.2 最佳对比区确定

古田试验区的主要天气系统为低涡切变、暖区辐合和高空槽,降水云系多为向东北方向移动的积层混合云[40]。由图3可知,红色方框为古田随机试验人工影响天气目标区,结合历史天气类型及云系主要移动路径,在目标区上游和侧方设计连续多个形状大小一样的区域为浮动对比区(蓝色方框)。基于历史自然降水数据,将20个浮动对比区与目标区进行面雨量相关性和地形相似度分析。考虑到地形变化对天气系统的影响因素,本文优先选择相关系数最高的区域,若相关系数相同,则优先选择地形相似度最高的区域作为最佳对比区(图3黑色方框),两区雨量相关系数为0.63,地形相似度为53.08%。

图3 古田随机试验目标区、浮动对比区与最佳对比区设置

3 不同统计方法的自然雨量关系模型对比

区域历史回归建立两区域雨量关系模型的目的是利用对比区的自然雨量合理预期目标区作业期的自然雨量,并将其与作业影响后目标区的降水实测值对比,确定增雨效果。通过引入机器学习,对比不同统计方法的自然雨量关系模型,基于最优雨量关系模型得到目标区最接近自然降水的降水估测值,进而得到人工增雨作业后的合理增雨量。

下文采用线性拟合、多项式回归、样条回归、机器学习进行对比分析[41-42]。选取均方根误差和确定系数比较不同拟合方法的优劣。均方根误差是回归模型的拟合标准差,越接近于0,模型预测结果越精准;确定系数反映因变量的变化能由自变量解释的比例,表征回归模型的可靠程度,其正常取值范围为[0,1],该数值越大,代表模型解释能力越强,对数据预测效果更好。

3.1 基于平均面雨量的多种统计关系模型对比评估

图4为不同雨强(I)的样本量。由图4可知,小时雨量主要集中在雨强小值区域。将降水分为4类:弱降水(0.1 mm·h-1≤I<5 mm·h-1)、一般降水(5 mm·h-1≤I<10 mm·h-1)、中等降水(10 mm·h-1≤I<25 mm·h-1)和强降水(I≥25 mm·h-1),其中弱降水样本量占比为95.98%,强降水占比仅为0.03%(表1)。

表1 2014—2023年不同等级降水样本量

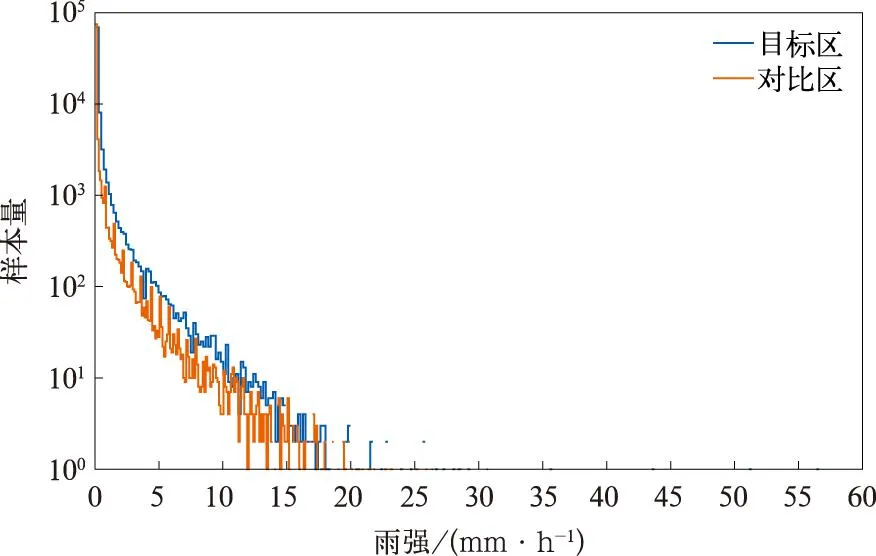
图4 不同雨强样本量统计

分别选取对比区小时平均面雨量和平均面雨量六次方根变换值作为预测变量,选取目标区小时平均面雨量和平均面雨量六次方根变换值作为响应变量,利用线性回归、多项式回归(二项、三项、四项、五项)和样条回归(回归次数分别为1、2、3、4)多种模型,对比不同降水等级样本和总样本数据的拟合结果,建立的回归模型均方根误差如图5所示。由图5可知,选取平均面雨量作为预测变量,一般降水和中等降水样本均方根误差为3.3～4.5 mm,总样本的均方根误差相对较小,约为1.1 mm,其次为弱降水数据。平均面雨量经六次方根变换后,总样本的统计结果同样表现相对较好,均方根误差相对较小。在后续分析中可以基于总样本进行统计分析,其中针对总样本构建相关模型时,四项式回归的均方根误差最小,其次为二次样条回归。

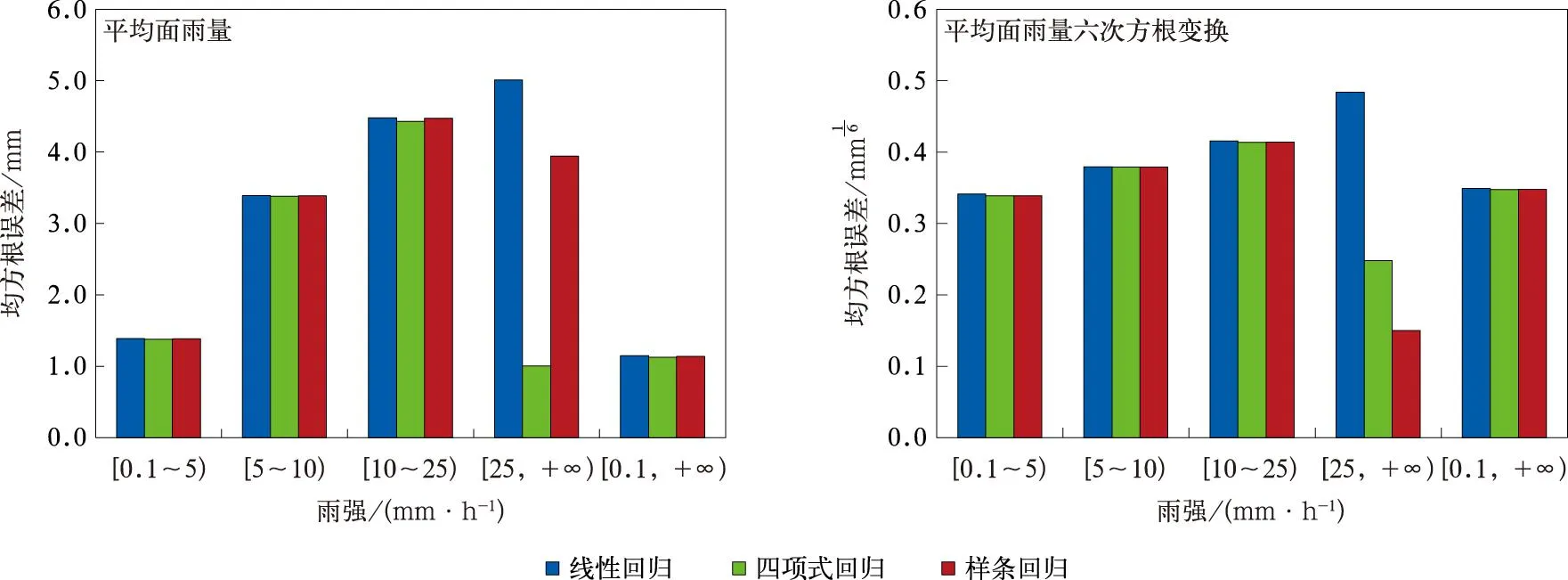
图5 不同雨强下各模型的降水估测均方根误差对比

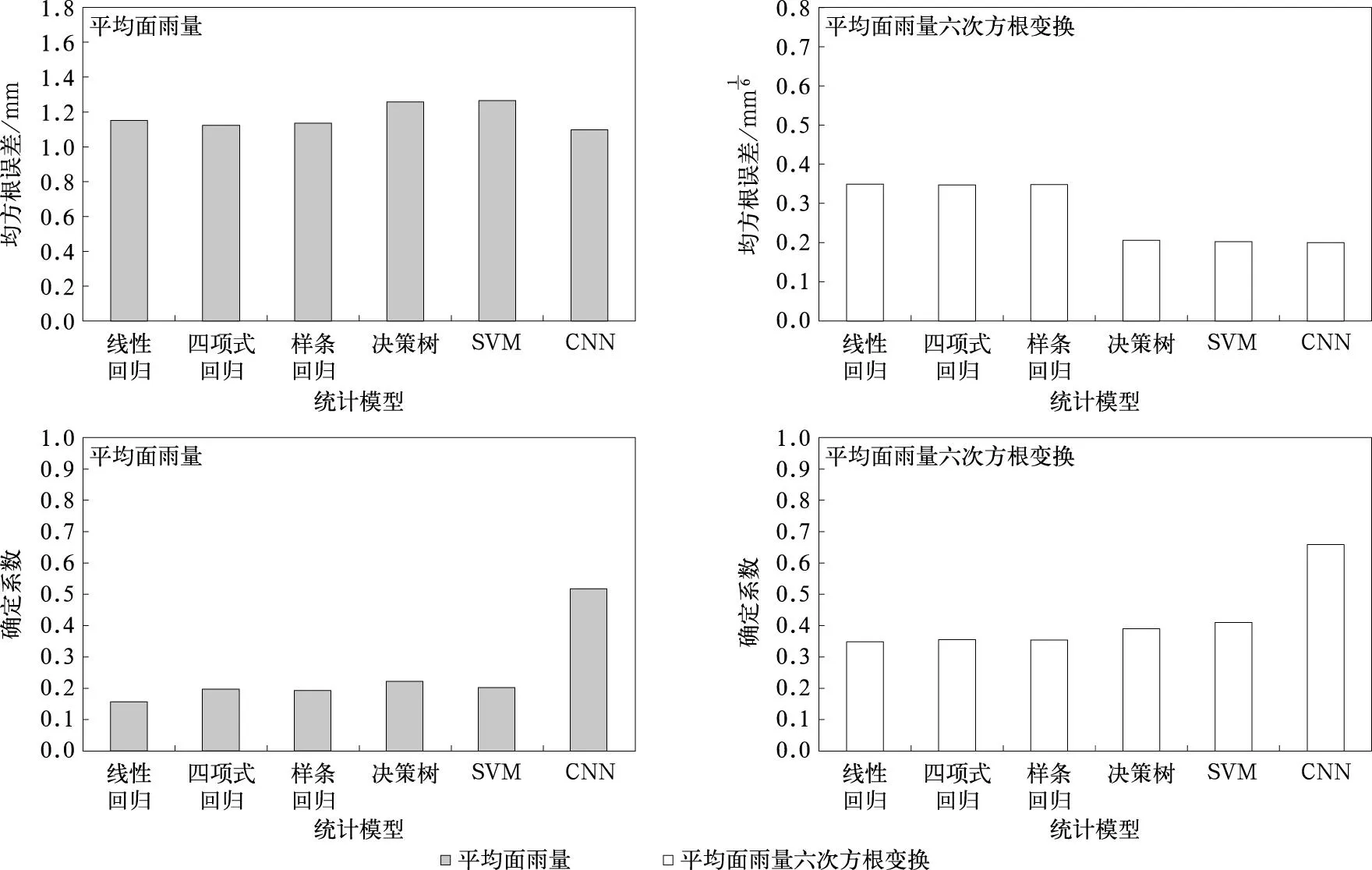
图6 基于总样本的不同模型降水估测的均方根误差和确定系数

3.2 基于面雨量空间格点的卷积神经网络机器学习关系模型

考虑到两区域面积较大,降水的空间分布明显不均,单纯以区域平均面雨量代表区域降水存在局限性,且两区域的上下游关系导致降水存在明显时间序列效应,同一降水过程目标区和对比区的欧式距离最近。因此尝试由点到点转化为面到面,利用CNN机器学习方法研究两区域面雨量关系,该模型能够涵盖云系的移向和移速,即降低欧氏距离的影响因素。如图7所示,目标区有33个自动气象站,对比区有18个自动气象站。对目标区和对比区进行空间均匀格点化,并利用反距离权重、克里金、线性和三次样条4种插值方法计算区域内面雨量空间分布。以2016年4月9日19:00(北京时,下同)为例,4种方法插值结果如图8所示。由图8可见,克里金插值法导致分析区域内18.9 mm的强降水中心丢失,整体面雨量分布偏小;线性和样条插值均存在边界效应,边界处的数据极易不稳定、失真;反距离权重方法能相对准确地反映降水强度空间分布特征,插值效果相对较好。

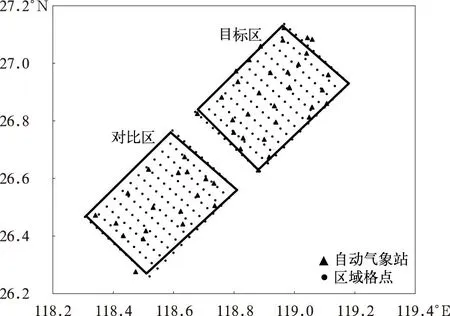
图7 目标区和对比区格点化及区域自动气象站分布

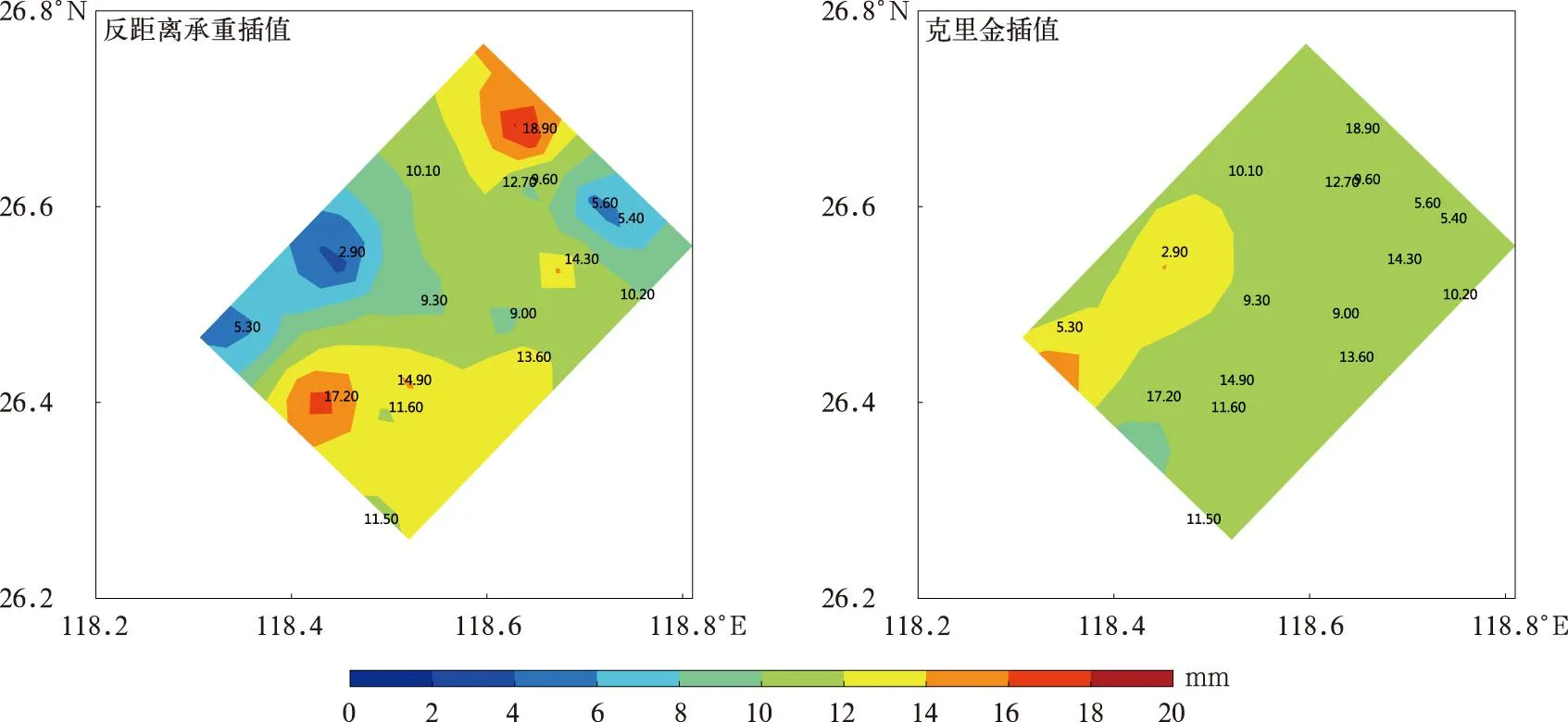
图8 2016年4月9日19:00不同插值方法得到的面雨量分布

基于面雨量空间格点数据,利用CNN建立对比区-目标区雨量最佳关系模型。CNN主要适用于解决图像处理、识别问题,无需事先提取特征,将图像的原始像素直接作为输入,大幅减少了传统方法所需的大量重复、繁琐的数据预处理工作。此外,卷积的局部感知、时空亚采样和权值共享结构能够大量减少需要训练的参数数量,避免过拟合且可以降低模型复杂度。各输入要素插值到格点上后用CNN提取特征,能更好地保留区域内云系生消发展过程中的移动、变化等特征,提高空间预测能力。

采用自适应矩估计、均方根传递和梯度随机下降3种不同优化器训练模型,通过调整过滤器和卷积核尺寸建立两区域小时面雨量格点数据关系模型。其中,自适应矩估计(简称ADAM)优化器是一种能够自适应地计算并调节每个参数学习率的方法,在均方根传递(简称RMSP)的基础上结合动量梯度下降的方法,实现快速收敛;梯度随机下降(简称SGD)优化器每次迭代随机选择1个样本进行训练,在样本量较大的情况下,能够极大加速每轮参数的更新速度。此处定义模型的均方根误差为整个区域面雨量格点值均方根误差的平均值。经过比较,ADAM优化器适合该模型,其均方根误差为0.61 mm,其次为SGD优化器,其均方根误差为0.67 mm。随机选取2019年1月20日20:00,2019年5月5日22:00和2022年3月2日03:00共3个个例,比较3种优化器的性能(图9)。由图9可知,个例1(2019年1月20日20:00) RMSP优化器估测的降水分布和强度偏差最大,雨量大于0.7 mm的区域面积明显偏大;个例2(2019年5月5日22:00) RMSP和SGD两种优化器得到的目标区降水估测值与实测值偏差亦相对较大,且RMSP优化器估测的雨强明显偏弱;个例3(2022年3月2日03:00) RMSP和SGD 两种优化器估测的降水估测值均偏大,且雨量大于0.6 mm的区域面积偏大。综上,基于ADAM优化器的目标区降水估测值与实测值较一致。

图9 3种优化器降水估测对比

4 结论与讨论

为进一步优化人工增雨作业效果统计检验方法,本文基于2014年1月—2023年1月小时降水数据,利用机器学习,结合线性拟合、多项式回归和样条回归等多种数学统计方法,建立目标区和对比区间不同雨量关系模型并进行对比分析,得到如下结论:

1) 古田随机试验目标区与其周围浮动对比区地形相似度和降水相似度呈较明显的正相关关系,结合降水云系主要移动路径,在目标区上游位置得到最佳对比区,雨量相关系数为0.63,地形相似度为53.08%。

2) 历史降水数据样本主要集中在弱降水等级,利用多种回归方法(线性回归、多项式回归和样条回归),采用分段雨强建立两区域间的线性回归模型改进不明显,其均方根误差普遍高于总样本的统计结果。

4) 基于面雨量空间格点数据,采用CNN 3种不同优化器(RMSP、ADAM和SGD)建立对比区-目标区雨量关系模型,其中ADAM优化器模型最优,利用对比区估算目标区自然雨量能力最强,其均方根误差为0.61 mm。

分析表明:CNN机器学习方法更适合于建立两区域间的雨量关系模型,且基于面雨量空间格点的机器学习雨量关系模型可在一定程度上消除平均面雨量进行六次方根变换时产生的量纲影响,并减少强降水中心的扰动。作为人工增雨作业效果定量评估的关键手段,可根据典型天气形势或主要移动路径分类细化模型,进一步提高目标区与目标雨量关系模型的可信度和准确度。