基于Seidel像差理论的离轴四反初始结构自动化设计方法研究

朱历伟，杨磊，陈洁，张文平，郭世亮，2，谢洪波

（1 天津大学 精密仪器与光电子工程学院，光电信息技术教育部重点实验室，天津 300072）

（2 天津大学-赛思倍斯空天光电系统工程联合实验室，天津 300072）

（3 赛思倍斯（绍兴）智能科技有限公司，绍兴 311899）

0 引言

反射式望远系统相比于折射式望远系统具有无色差、布局灵活、口径大等优势，在空间探测、遥感等领域有广泛的应用［1-4］。反射式望远系统又可以分为同轴反射式和离轴反射式两种类型。同轴反射式结构可以实现长焦距，但是由于遮拦的原因无法实现宽视场导致光能的利用效率降低。离轴反射式结构可以同时兼顾长焦距、宽视场和高成像质量的特性，适用的应用场景更多［5］。

离轴反射式望远结构通常以包含的镜片数量来定义，例如离轴三反、离轴四反结构等。当前，最典型的应用形式是离轴三反结构，但其存在优化自由度相对较少的问题，很多场合达不到应用需求［6］。相较于离轴三反结构，离轴四反结构增加了设计自由度，对像差平衡和矫正能力更好，更容易实现小摄远比。随着光学加工和装调技术的不断发展，离轴四反结构的应用成为未来的发展趋势之一［7-8］。

离轴反射式结构一般需要在光学设计软件中建模和优化。目前光学设计软件的优化往往需要一个三阶像差矫正良好的光学系统作为初始结构［9-12］。由于软件的局部优化采用的是阻尼最小二乘法，设计结果往往会陷入局部最优解而无法跳脱出来。因此，快速获得多个三阶像差矫正良好的光学系统对后续优化有着至关重要的作用。QU Zheng 等［13］提出了一种基于模拟退火的光学系统设计方案，此方法通过建立关于矢量像差理论的像质评价函数以及体积约束的评价函数来实现，并利用模拟退火的全局优化算法来实现紧凑型高分辨反射式光学系统的设计方案。XU Fenggang 等［14］提出使用遗传算法求解特定布局的同轴四反初始结构，可以为四反射光学系统提供像质良好的设计起点。YANG Tong 等［15］提出了基于深度学习的自由曲面离轴三反光学系统设计方案，对于训练完成后的神经网络，只需要输入给定的系统参数，就可以输出对应的表面数据。但是目前研究中较少涉及到离轴四反初始结构的设计方法。

本文提出一种离轴四反光学系统初始结构建立的新方法，在设计之初选择合理的视场偏置来实现离轴，引入光线传输矩阵来简化近轴光线的追迹过程。通过计算每一面上的近轴光线信息来求出Seidel像差，以Seidel像差绝对值最小化作为评价的目标函数。同时，利用粒子群优化算法实现初始结构的多参数求解，并通过MATLAB 和CODE V 之间的数据交互来分析初始结构遮拦情况，获取理想的初始结构。在确定初始结构后逐步增大入瞳以及拓宽视场角，同时引入XY多项式自由曲面以及引入偏心和倾斜量进一步矫正离轴像差，演示了一款长焦距、宽视场的离轴四反光学系统设计实例。

1 设计原理

建立同轴四反初始结构通常有两种基于Seidel像差理论的推导方法。一种是通过放大率、遮拦比以及二次曲面系数来推导出初级像差表达式，并求解出同轴四反初始结构，再通过视场偏置和孔径离轴实现最终的离轴四反结构。该方法求解过程相对复杂而且需要对放大率和遮拦比等参数做出限定。第二种方法是在同轴三反的基础上，通过在最后一面加入平面镜来实现同轴四反初始结构的建立。此种方法虽然计算简单但是由于缺少自变量个数很难有效地对特定条件进行约束。

相较于传统方法，本文提出了一种通过视场偏置实现无遮拦离轴反射初始结构建立的思路。通过计算每一个面上主光线和边缘光线的光线信息来求出三阶Seidel像差，利用粒子群优化算法求解出使得三阶Seidel像差绝对值之和尽可能小的解。在此基础上联合使用CODE V 和MATLAB 软件，通过视场偏置自动挑选出符合无遮拦条件的初始结构供后续优化使用。

1.1 Seidel像差计算

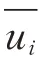
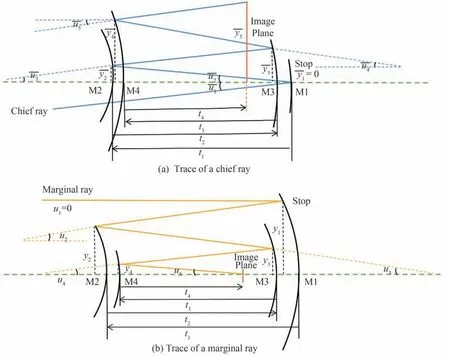
图1 同轴四反结构光线追迹示意图Fig.1 Ray tracing of the initial coaxial four-mirror structure

为了简化计算，引入光线传输矩阵。由于近轴面的光线追迹属于线性运算，所以可以使用矩阵的方式来进行近轴光线的表示和追迹。面与面之间存在角度和光线高度的传递关系，用代数公式表示为

式中，y和y′表示折射前后在镜面上的光线高度，u和u′代表折射前后光线的角度，t′代表镜面之间的间隔，n和n′代表折射前后的折射率，ϕ代表镜面的光焦度。

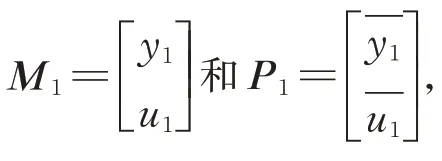
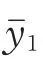
根据Seidel像差理论，对于旋转对称的光学系统，可以利用近轴光线的追迹结果来表示五种单色像差。球差SI、慧差SII、像散SIII、场曲SIV和畸变SV的表达式分别为

式中，c代表镜面的曲率，A和分别代表边缘光线和主光线的折射不变量，Δ 表示折射前后物理量之差，H代表系统的拉格朗日不变量。它们的计算公式分别为

1.2 结合Seidel像差理论构建评价函数

传统求解初始结构的方法是在同轴的情况下使光学系统某几项的Seidel像差为零作为条件来联立方程式进行求解，当定义的约束条件变多时，可能不存在使得Seidel像差都为零的情况。此时可以将求解方程零点的问题转化为求解目标函数最小值的问题。目标函数就是使得这五种初级像差系数绝对值之和最小，同时加入一些限制条件，比如后截距和焦距的要求，构建一个含有混合约束的单目标优化问题。由于设计指标中往往会对后截距以及系统的焦距有限制，所以将系统的焦距以及后截距都用半径参数ri以及镜面间隔参数ti表示。具体的数学模型为

式中，F(xi)是需要求解的目标函数，当三阶Seidel像差值越小时，光学系统表现出来的光学性能更优越。因此将三阶Seidel像差绝对值加权之和作为构建初始结构的评价函数，wi(i=1，2，3，4)代表三阶Seidel像差在评价函数中的权因子，若某一项Seidel像差对应的权重更大，则求解的初始结构中该Seidel 系数也相应的越小。若希望初始求解的系统可以尽量消除SI～SIV，但是不考虑SV的影响，那么就可以增大w1～w4的权重，同时减小w5的权重或者将其设置为0。hj(x)代表光学系统布局中等式的约束条件，比如对系统焦距的约束，m代表等式约束的数量。gi(x)代表光学系统布局不等式的约束条件，比如小型化、一体化等约束，p代表不等式约束的数量。最后对设计变量xi本身约束，包括曲率半径ri和镜面间隔ti。其中li为设计变量的下界，ui为设计变量的上界，q代表设计变量约束的数量。通过构建单目标混合约束的优化模型，可以将求解光学系统初始结构的问题转化为求解目标函数的最优化问题。

1.3 基于粒子群优化算法求解初始结构

粒子群优化算法（Particle Swarm Optimization，PSO）是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法［16］。具体的算法流程如图2所示。

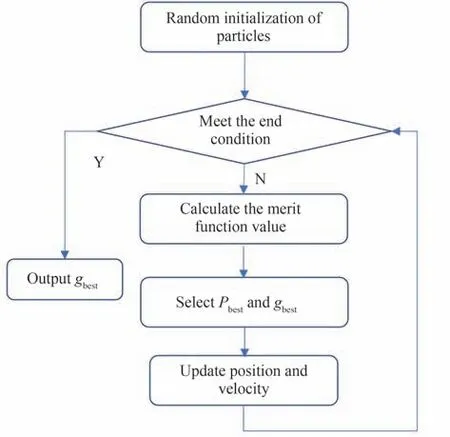
图2 粒子群优化算法流程Fig.2 Flow chart of particle swarm optimization algorithm

粒子群优化算法通过设计一种无质量的粒子来模拟鸟群中的鸟。粒子有两个基本的属性：速度和位置。速度代表粒子下一步迭代时移动的方向和距离，位置是求解问题的一个解。鸟被抽象为无质量的一个粒子点并扩展到N维空间中，粒子i在N维空间中的位置矢量为Xi=(x1，x2，…，xN)，飞行速度矢量为Vi=(v1，v2，…，vN)，每个粒子都有一个由目标函数决定的适应度，并且知道目前自身最好的位置(pbest)和现在的位置Xi。除此之外，每个粒子还知道目前整个种群中所有粒子发现的最好位置(gbest)，这个可以看成粒子同伴的经验。粒子就是通过自己本身的经验以及整个种群中的最好经验来决定下一步的运动。

粒子群优化算法是从随机解出发，通过迭代寻找最优解，相比于遗传算法，粒子群算法具有收敛速度快、参数少、算法简单易实现的优点，非常适用于高维度的非线性优化问题。因此使用粒子群优化算法来实现式（8）中所表示的目标函数。但粒子群优化算法受到很多因素的影响，其中粒子初始值对最终结果的影响较大，因此采取大量生成随机初始点的方法对结果进行分析比较并且挑选出目标函数较小的解的结果 。

1.4 无遮拦初始结构建立及优化

实现离轴的方式主要有三种，分别是视场偏置、孔径偏置以及视场和孔径偏置同时存在的情况。采用视场偏置的方式来构建初始的离轴系统，具体算法如图3所示。首先，预先给定一个初始的视场偏置，通过粒子群优化算法对目标函数进行求解，求出多组可行解，将求出的曲率半径以及镜面间隔导入到CODE V中，读取相应点的坐标位置并且传递到MATLAB 中进行数据处理。如果点线之间的位置关系满足相应的条件，说明此时的结构满足无遮拦的情况；如果此时并没有找到合适的无遮拦的初始结构，那么就改变视场偏置的大小，重新寻找最优解以及判断是否满足相应的点线位置关系。在此基础上通过增加视场角以及增大入瞳直径来达到期望的设计指标要求，并引入高阶偶次非面以及自由曲面来完成最终的设计。

图3 无遮拦初始结构挑选以及优化流程Fig.3 Unobscured initial structure selection and optimization flow chart

2 离轴四反光学系统设计实例与分析

2.1 离轴四反光学系统基本参数

基于构建的模型设计一款宽视场离轴四反光学系统，其具体的设计指标如表1所示。

表1 离轴四反光学系统设计指标参数Table 1 Parameters of off-axis four-mirror optical system

2.2 离轴四反初始结构求解

为了建立合适的初始结构，根据式（8）建立的数学模型，以Seidel像差绝对值的加权和最小化作为目标函数，同时将Seidel像差的各项权重wi均设为1。在系统中加入对系统焦距和后截距的限制，并且考虑到系统整体小型化的要求，对其中的镜子间隔也做了相应的控制，其数学模型为

式中，dBFL和fEFL分别代表系统的后截距和焦距。由于系统最终要求的入瞳直径较大，如果开始就以此入瞳大小作为条件去求解很难得到有效的无遮拦初始结构。因此可以选择以较小的入瞳直径最为初始条件进行带入求解，在得到无遮拦初始结构之后再逐步增加入瞳直径来满足最终的F数要求。同时，也要合理考虑视场偏置的大小，若视场偏置较小则很难实现离轴，若视场偏置过大则会导致离轴的非对称像差增大，不利于后续的进一步优化。

在综合考虑入瞳直径和视场偏置对构建无遮拦离轴四反初始结构的影响之后，选取焦距为1 200 mm、入瞳直径为70 mm、存在7°视场偏置的光学系统求解初始Seidel像差最小时的解。在图4 中给出了4 次不同初始值迭代后的最终效果，迭代均收敛到一个比较好的效果，说明采用粒子群优化算法来实现此类问题的求解是有效的。

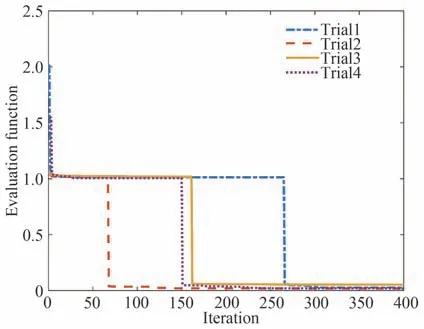
图4 不同初始值误差函数迭代曲线Fig.4 Error function iteration curves with different initial values

表2 和表3 中给出4 次不同初始值情况下的解以及对应的Seidel像差的值，计算得到的Seidel像差的值与光学设计软件中所给出的值也是完全吻合的。

表2 离轴四反光学系统初始解Table 2 Initial solutions of off-axis four-mirror optical system

表3 初始解对应的Seidel像差Table 3 Seidel aberration corresponding to the initial solution

将数据进一步导入到CODE V 软件中，通过MATLAB 调用底层的API 接口获取光线在镜面上坐标点位置，并根据点线之间的位置进一步判断此时是否存在遮拦的情况。图5 是某一视场偏置条件下得到的离轴四反的初始结构，为了清楚说明结构约束的边界条件，只给出了上、下边缘光线的光束。当系统完全无遮拦时，应当满足式（10）6 个约束条件。需要强调的是这6 个约束条件只针对图5 的结构布局才成立，针对其他构型的离轴四反结构形式则需要满足其他类型的结构约束条件，不再一一列举。

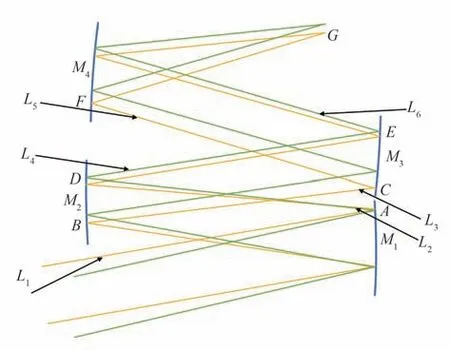
图5 离轴四反初始结构示意图Fig.5 Off-axis four-mirror initial configuration layout

如果得到的点线之间的距离满足式（10）的约束条件，说明此时系统的结构满足无遮拦的条件，就将当前的解保存下来；如果不满足其中一个约束条件，则将当前的解舍弃。通过此方法，可以挑选出多种光焦度分配以及不同结构类型的无遮拦离轴四反初始结构方案。图6 给出了4 种不同结构类型的离轴四反示意图，可以看出不同解所得到的离轴四反初始结构的体积也完全不同，可以从中挑选出合适的尺寸进行下一步优化。

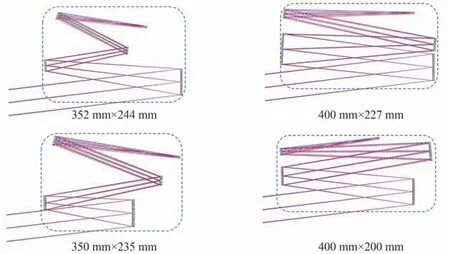
图6 不同解对应的离轴四反初始结构Fig.6 Off-axis four-mirror initial structures corresponding to different solutions

2.3 利用光学设计软件进行优化

在获得离轴四反初始结构的基础上，利用光学设计软件进一步优化。为了增加优化的自由度，在优化过程中往往会加入偏心和倾斜作为优化变量矫正像差。但是在优化过程中如果不限制让其自动优化，优化的趋势往往趋于共轴，使得光线发生遮挡。如图7所示，次镜的下边缘有可能在优化过程中与三镜和四镜之间的光线发生遮挡。因此，为了避免光线遮挡，需要在优化过程中仍然满足式（10）中提到的约束条件。利用CODE V 自带的宏函数实现自动求解点线之间的距离，并以此作为约束条件加入到优化宏之中，这样在优化过程中可以避免遮拦的情况。

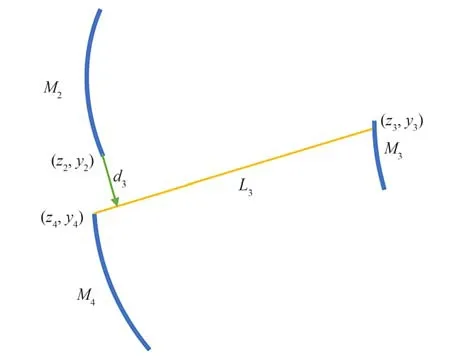
图7 边缘光线位置控制示意图Fig.7 Layout of edge ray position control

由于在构建初始结构时设置的入瞳直径和视场较小，因此在优化阶段需要逐步扩展入瞳直径以及视场角大小来满足设计指标要求。一般来说，若初始的入瞳直径和视场与最终的设计指标之间存在较大差异，采取手动改变入瞳直径和增加视场再逐步优化的方法会耗费大量的时间；如果选择每次增加较大的入瞳直径和视场则会容易导致陷入局部最优解或者光线追迹出现错误。

为了解决手动增加入瞳直径和视场过于繁琐的问题，联合使用MATLAB 与CODE V 软件，避免大量重复性的优化过程。通过MATLAB 调用CODE V 底层API 实现两个软件之间的数据交互，可以修改系统参数（入瞳直径、视场角等）。同时，将优化离轴四反的程序以宏文件的形式进行保存，方便在MATLAB 中通过宏文件来实现离轴四反的优化。通过此方法，可以更快速更高效地实现系统从小入瞳、小视场到大入瞳、大视场的扩展。

优化过程如图8所示，同时利用优化宏着重控制光线和镜面之间不发生遮拦；在此基础上，利用非球面和自由曲面来达到所需要的性能指标要求。

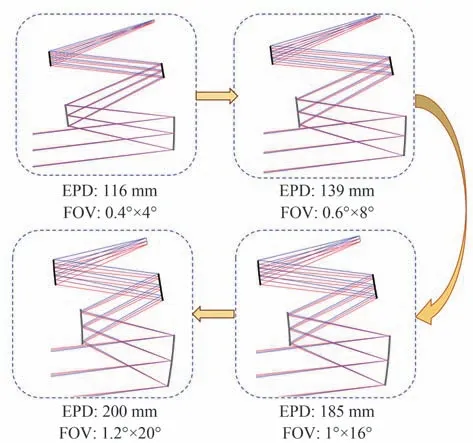
图8 逐步扩展入瞳直径和视场角的优化过程Fig.8 The optimization process of gradually expanding entrance pupil diameter and field angle

将优化的面型由球面优化为非球面，再从非球面优化为XY多项式自由曲面，通过不断的迭代优化，最终得到焦距为1 200 mm、F数为6、子午方向为±0.6°和弧矢方向为±10°的离轴四反光学系统，如图9所示。由图可知，系统结构布局紧凑，成像质量良好，各视场的调制传递函数（Modulation Transfer Function，MTF）在60 lp/mm 处均大于0.5。

图9 优化后的离轴四反结构Fig.9 Optimized off-axis four-mirror structure

3 结论

本文基于Seidel像差理论，利用近轴光线追迹方法，推导出同轴四反结构的Seidel像差公式。将求解同轴四反初始结构问题转化为求解非线性单目标函数的优化问题，利用粒子群优化算法对目标函数求解，获得多组不同光焦度分配的初始结构。在此基础上联合使用CODE V 和MATLAB 软件，通过视场偏置挑选出无遮拦的离轴四反结构，并在此基础上逐步增大入瞳以及拓宽视场角，同时引入XY多项式完成最终的优化设计，成像系统MTF 接近衍射极限。该方法可以快速获得不同光焦度分配以及体积大小的离轴反射式初始结构，可为后续的优化提供良好的设计起点。