Control Strategies for Digital Twin Systems

Guo-Ping Liu ,,

Abstract—With the continuous breakthrough in information technology and its integration into practical applications, industrial digital twins are expected to accelerate their development in the near future.This paper studies various control strategies for digital twin systems from the viewpoint of practical applications.To make full use of advantages of digital twins for control systems, an architecture of digital twin control systems, adaptive model tracking scheme, performance prediction scheme, performance retention scheme, and fault tolerant control scheme are proposed.Those schemes are detailed to deal with different issues on model tracking, performance prediction, performance retention, and fault tolerant control of digital twin systems.Also, the stability of digital twin control systems is analysed.The proposed schemes for digital twin control systems are illustrated by examples.

I.INTRODUCTION

WITH the rapid development of information technology,the application scope of digital twins continues to expand.Simply speaking, the digital twin, which is a concept originating from industry, refers to the construction of completely consistent corresponding models, dynamic simulation,monitoring, analysis and control of physical entities in the real world through digital means.The digital twin emphasizes simulation, modelling, analysis, and decision-making of physical entities in the data world.Since this concept was proposed,digital twin technology has been evolving rapidly and had a huge driving effect on product design, manufacturing, and service.The digital twin is an innovative application that integrates various technologies, such as the Internet of Things,cloud computing, big data and artificial intelligence [1].It can widely be applied in various sectors, e.g., manufacturing,energy, transportation, healthcare and agriculture, to improve efficiency, reduce costs, and enhance competitiveness.

The concept of digital twins can be traced back to the mirrored spaces model proposed in 2003, which is defined as a three-dimensional model that includes physical products, virtual products, and the connection between the physical and virtual products [2].Due to limitations in technology and cognition level at the time, this concept was not given much attention [3], and no related achievements were published in the following decade.In 2010, National Aeronautics and Space Administration (NASA) first introduced the concept of digital twins in the space technology roadmap with the aim of using digital twins to achieve comprehensive diagnostic maintenance of flight systems [4].In 2011, the US Air Force Laboratory clearly proposed a digital twin example for future aircraft,pointing out that a complete virtual mapping of aircraft should be built, based on the high-precision simulation model, historical data and real-time sensor data of aircraft, so as to achieve the prediction of aircraft health status, remaining life and mission reachability [5].Afterwards, the concept of digital twins began to receive widespread attention, and some research organisations began to study related key technologies [6], [7].The applications of digital twins also expanded from aircraft operation and maintenance to rich scenarios, such as product development, equipment manufacturing, and smart cities[8]-[10].As a rapidly developing emerging technology, digital twins have extensively been studied in terms of data fusion, modelling, control and other aspects.

Accurate modelling and control of digital twins require sampling data.In practice, digital twin systems are located in complex environments, and their sensing data have characteristics, such as multi-sources, heterogeneous, multi-scales, and high noises.Therefore, it is necessary to clean the data and handle issues, such as loss, redundancy, conflicts, and errors of data through various algorithms, e.g., machine learning algorithms with rule constraints.At the same time, the data collected by multiple sensors should be fused to improve the robustness and reliability of twin data and expand the modelling dimension of virtual entities [11].The common multisensor fusion methods include fuzzy logic, neural networks,wavelet analysis, support vector machines [12], [13], etc.In digital twins, sensor data and models are typically fused and mapped on the basis of methods such as IoT middleware, feature extraction, and information fusion.For example, a model fusion method has been proposed to fuse multi-sensor data into a single model [14], based on semantic feature fusion,combining the characteristics of computer-aided design systems, computer-aided manufac-turing systems, etc.Digital twin modelling is to create a high-precision virtual model to truly reproduce the geometry, attributes, behaviour and rules of a physical entity [15].These models should not only be consistent with a physical entity in geometric structure, but also be able to simulate its spatiotemporal states, behaviours,and functions [16].A five-dimensional digital twin model has been proposed [17], consisting of physical entities, virtual entities, connections, twin data and services.It emphasizes the driving role of twin data composed of physical data, virtual data, service data and knowledge on physical entities, virtual devices and services.The application ideas and schemes of the five-dimensional digital twin model in multiple fields are widely recognized.

Digital twin-based control has been studied to improve the control performance of a system in recent years.A digital twin-based optimal state control method has been proposed to help a synchronized production operation system keep in an optimal state when uncertainties affect the system for obtaining the full element information needed for decision making[18].A transparent digital twin has been designed for output control using the belief rule base, which is not only to model the complex relationships between the system inputs and output but also to conduct output control by identifying and optimizing the key parameters in the model inputs so that iterative optimizations are not necessarily needed [19].A physicsbased digital twin allows a digital twin instance for model predictive control of autonomous unmanned aerial vehicle landing to be informed by a truly dynamic flight model, rather than a less accurate set of steady-state aerodynamic force and moment data points [20].A digital twin-driven method for online quality control in process industry has been presented to realise real-time monitoring, evaluation, and optimization of process parameters that are strongly related to product quality [21].A web-based digital twin thermal power plant has been developed to provide a feasible and practicable route for monitoring and control of a thermal power plant via web browsers, processing data, visualizing processes, and sending commands to the control systems of the plant [22].There are some similar concepts to digital twin control, for example, the optimal-tuning control [23], [24] and parallel control [25],[26].The research work above has accelerated the use of digital twins in control systems.

Digital twins have been applied in scenarios, such as the service industry, supply chain management, intelligent workshops, product research and development, fault diagnosis, and smart cities.The research based on service theory enables digital twins to provide optimal services to customers.For example, a digital twin model was constructed for specific service applications based on a metamodel in unified modelling language (UML) format, providing services for the full lifecycle management of batteries [27].Introducing the digital twin model into supply chain management monitors and predicts real-time changes in the supply chain to simplify business processes and improve decision-making efficiency [28].The world’s largest bearing manufacturer has applied the digital twin model to its distribution network [29].Being driven by twin data in a workshop achieves the production management,activity planning, process control of the workshop [30], etc.,effectively improving the transparency of the workshop production and optimizing the production process [31], [32].Digital twins can improve the efficiency of equipment development and production in manufacturing enterprises through virtual simulation of manufacturing equipment and processes[33], [34], and provide the product quality inspection and support for managing and upgrading products throughout their entire lifecycles [35].Fault prediction and maintenance of equipment are carried out, based on digital twins.By updating the operation data, fault data and maintenance data of a physical entity, its losses are calculated, the remaining life of equipment is predicted, and maintenance decisions are guided.In addition to the aforementioned fields, digital twin technology has potential applications in satellite/space communication networks, environmental protection, military operations,and other fields.

Although digital twins have made significant progress in recent years, there still exist a number of challenges on modelling, prediction, control of digital twin systems.Generally,digital twins are dynamic and need to interact with the data of the physical entity layer in real time, integrate the virtual and real, and evolve the model iteratively.In the future, the digital twin model will still need to strengthen research in several areas, such as aligning with industry standard architectures,establishing unified description methods and specifications.How to effectively and deeply combine high-precision sensing data with system mechanisms to achieve better state evaluation and system characterization is an urgent problem to be solved.Also, for faults of a real system, how to improve fault tolerance of the system using digital twin techniques is an important issue.To tackle those challenging issues above, this paper proposes various control strategies for digital twin systems, including the architecture of digital twin control systems, adaptive model tracking scheme, performance prediction scheme, performance retention scheme, and fault tolerant control scheme.The stability of digital twin systems is also analysed.Comprehensive simulations are provided to demonstrate the effectiveness of the proposed control strategies for digital twin systems.

II.ARCHITECTURE OF DIGITAL TWIN CONTROL SYSTEMS

Following the previous work on the optimal-tuning proportional integral derivative (PID) control method [23], [24],[36], a digital twin control system is presented, as shown in Fig.1.This system mainly consists of three parts: 1) The physical subsystem that is a physical closed-loop feedback control system with a real plant and a controller; 2) The virtual subsystem that is a virtual closed-loop feedback control system with a digital plant and a controller; 3) The information exchange between the physical and virtual subsystems.In this digital twin control system, the real plant represents the practical process or plant to be controlled, and the digital plant is the model of the real plant, which can be identified off-line and/or on-line to track the dynamic variations of the real plant.The controller for the digital plant, denoted as D-controller,has the same structure as the controller for the real plant,denoted as R-controller, and the parameters of the former can be passed to the latter if needed.In fact, the real plant and digital plant are twin, and the R-controller and D-controller are twin as well.So, the physical subsystem and virtual subsystem are also twin.

Generally speaking, the digital twin control system is aimed to construct a corresponding digital control system with the same dynamic characteristics as a physical control system in the real world, fully utilizing physical mechanisms, sensing information and operational data.Through digital means, the physical control system can dynamically be simulated,tracked, monitored, diagnosed, predicted, analyzed, synthesized, etc.

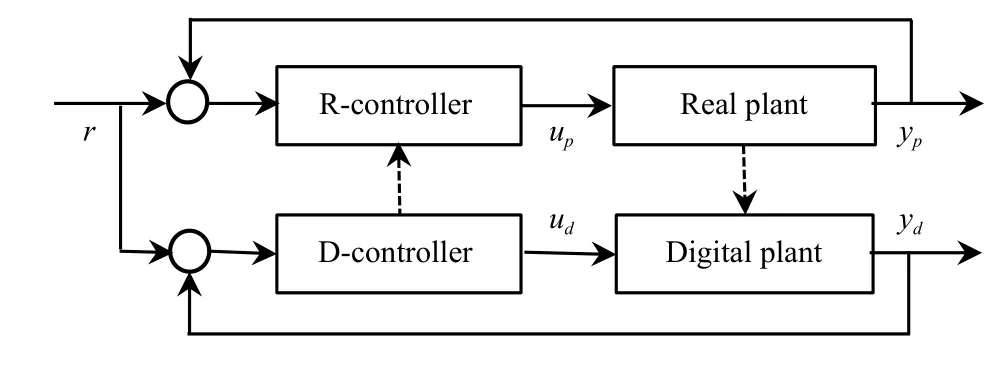
Fig.1.The digital twin control system.

The real plant (or process) is described in a discrete form of

wherexp(t),yp(t) andup(t) are the state vector, output vector and control input vector of the real plant, respectively,θpand φpdenote the parameters of the real plant,f(·) andg(·) are the nonlinear function vectors,nandmare positive integers, andv[k](t) of a signalv(t) is defined as

fork≥0.

In most cases, the nonlinear function vectorsf(·) andg(·) of the real plant are unknown.Thus, the digital plant is modelled as

wherexd(t),yd(t) andud(t) are the state vector, output vector andcontrolinput vectorof thedigital plant, respectively,θdandφdareits parameters,andfˆ(·)andgˆ(·)arethe nonlinear function vectors.In the digital twin control system, the digital plant should track the dynamics of the real plant as accurately as possible.

Utilising nonlinear modelling methods, e.g., neural networks, the nonlinear function vectorsfˆ(·) andgˆ(·) of the digital plant can be approximated by

and the weight matrices of the basis function vectors are set to θd,1=A, θd,2=Band φd,1=C, whereA,BandCdenote the matrices of a state space model.

The controller for the plant can be any kind of controllers,e.g., a PID controller, predictive controller and robust controller.A generic R-controller is described in the form of

wherezp(t) is the state vector of the controller,hpandkpare the controller parameters,H(·) andK(·) are the nonlinear function vectors of the R-controller,landqare positive integers, andr(t) is the reference input.

Normally, the controller of the digital plant should have exactly the same structure as the one of the real plant.So, the D-controller is

wherezd(t) is the state vector of the D-controller,hdandkdare the controller parameters.This controller should be designed to satisfy certain specifications, which include both system stability and control performance, using linear or nonlinear control methods.

For a linear proportional integral (PI) controller, the controller functionsH(·) andK(·) can be designed in the form of

wherez(t) represents the variableszp(t) andzd(t),y(t) represents the variablesyp(t) andyd(t) ,hdenotes the parametershzandhe, andkdenotes the parameterskzandke.

In the digital twin control system, there exists the information exchange between the physical subsystem and virtual subsystem.Firstly, the relationship between the real pant and digital plant can be represented by

where θ ˆd(θp,φp) and φ ˆd(θp,φp) are the functions of the parameters θpand φpof the real plant, which means that the model of the digital plant is related to the dynamic variations of the real plant.Generally speaking, the relationship (13) and (14)between the real pant and digital plant is unknown, but can be estimated by the method in Section III.

Secondly, the relationship between the R-controller and Dcontroller is generally denoted by

For the digital twin control system shown in Fig.1, compared with conventional control systems, there are serval advantages in the following aspects: dynamics tracking, performance prediction, performance retention, and fault tolerant control of the real plant.These will be addressed in the following sections.

III.ADAPTIVE MODEL TRACKING

As the dynamics of a real plant may change with time or there may exist some uncertainties in the real plant (1) and (2),the model of the digital twin system should track the variations taking place in the plant.To keep both the digital and real plants having the same dynamics, an adaptive model tracking scheme is presented in Fig.2, where the model parameters of the digital plant are adaptively updated with the dynamic variations of the real plant.

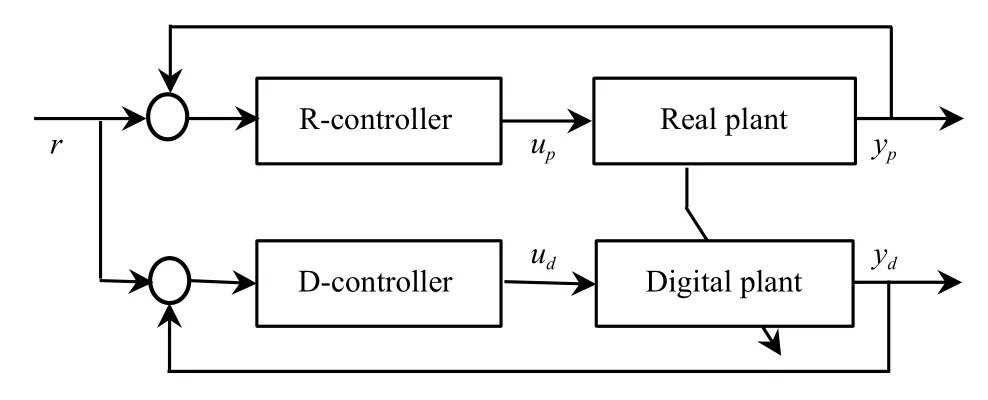
Fig.2.Adpative model tracking of the real plant.

Here, it is assumed that the structure and parameters of the R-controller and D-controller are exactly the same.Let the cost function of the model tracking be defined as

where the state error and output error are defined as

Generally, it is hard from the above to obtain the explicit expressions of the model parameters for the digital plant.Actually, the adaptive model reference control method can be employed to update the model of the digital plant.In this case,the reference model is the real plant.

The model tracking can also be realised by system identification methods.Now, a single-input single-state single-output real plant is considered.Let the functionJ(·) be

where αkand βkare the time-varying weighting factors, which are chosen to balance the requirements on both the state error and the output error of the digital twin control system at timek.Also, let the model of the digital plant be expressed by (5)and (6) with a single input and a single output, which can be re-written as

where

For the model tracking cost function (23), application of(21) and (22) to (17) results in

where λθ∈(0,1] and λφ∈(0,1] are the forgetting factors.Following the recursive least squares algorithm [37], the parameter θdcan recursively be estimated by

whereTθ(-2) is any positive definite matrix.

Similarly, the parameter φdcan also be estimated utilising the above algorithm, that is

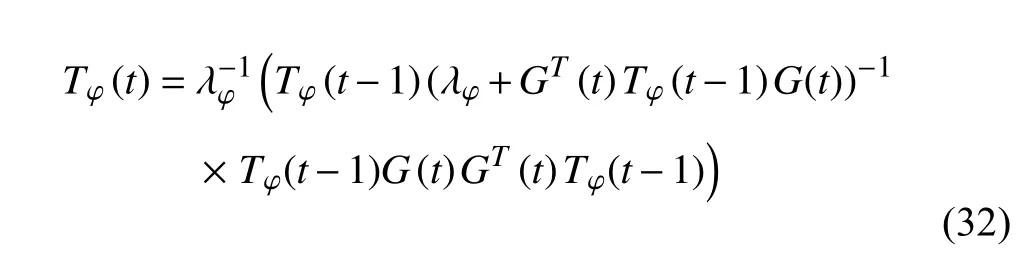
whereTφ(-1) is any positive definite matrix.

IV.PERFORMANCE PREDICTION

The performance prediction of the real plant plays a very important role in control and scheduling of a digital twin system.Using the virtual subsystem, the future behaviour of the physical subsystem can be simulated in advance before the next sampling time.A performance prediction scheme is presented, as shown in Fig.3.In this scheme, based on the information available up to timet, the future states, outputs and control inputs of the real plant fromt+1 tot+Ncan be predicted, whereNis the prediction length.

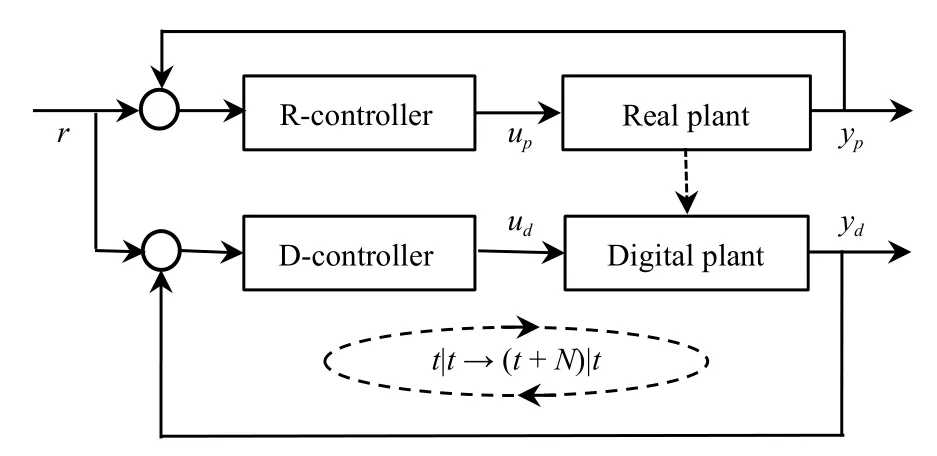
Fig.3.Performance prediction of the real plant.

To make the presentation simple, it is assumed that the digital plant tracks the real plant very closely, and the structure and parameters of the R-controller and D-controller are exactly the same.Two cases are considered here.

A. The Plant States are Measurable

Given the state vectorxp(t), output vectoryp(t) and control input vectorup(t) of the real plant up tot, and reference inputr(t) up tot+N, the multi-step predictions of the state, output and control input vectors of the digital plant [38] are recursively calculated by

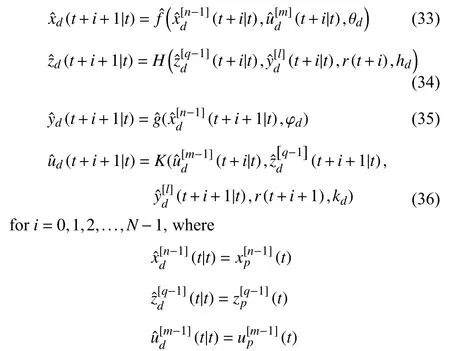
(t+i|t)represents thei-th step ahead prediction of the signalv(t) at timet,

B. The Plant States are Unmeasurable

If the states of the real plant are not measurable, a state observer is employed, i.e.,

whereLis the observer gain matrix.If the nonlinear functionsf(·) andg(·) of the plant are unknown, the state observer is structured by

In this case, the prediction calculations of the states, outputs and control inputs of the digital plant are the same as those used in Case 1 except that

In the two cases above, since the virtual subsystem tracks the physical subsystem, the predictions of the states, outputs and control inputs of the real plant can approximately be estimated by the following:

In this way, the performance prediction scheme can predict the performance (the states, outputs and control inputs) of the real plant through the virtual subsystem in advance.The prediction accuracy depends on how the model of the digital plant tracks the dynamics and environment of the real plant accurately.

V.PERFORMANCE RETENTION

Since the dynamics and environment of a real plant often vary with time, the system performance may degrade from its desired one.To deal with this issue, a performance retention scheme is proposed, as shown in Fig.4.

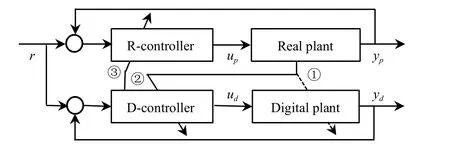
Fig.4.Performance retention of the real plant.

In practice, there are several objectives which a digital twin control system needs to achieve.The corresponding cost function vector of the control performance for the physical subsystem is denoted by

where ϕi(t,αp) is thei-th individual cost function of the real plant, αp={hp,kp} is the R-controller,nris a positive integer.

The performance criterion of the physical subsystem may practically be stated as

whereJ∗is the desired performance vector and ε is the tolerable performance error vector.

If the real plant is unknown, it is hard to search the controller parameters to satisfy criterion (40).To avoid this difficulty, an alternative cost function vector of the control performance is defined via the virtual subsystem as follows:

In addition, there may still exist some freedom for the controller design after satisfying criterion (40).Taking advantages of the digital twin control system, the optimal parameters of the controller may be formulated as

fori=1,2,...,nr, whereWdis the weighting matrix and is normally chosen as

The optimization problem given in (42) and (43) can be solved by employing optimization methods [39], for example,the method of inequalities.

When one of the following criteria fails:

VI.FAULT TOLERANT CONTROL

The digital twin control system has more advantages than a conventional control system on coping with system faults.This is because there exists a virtual subsystem in the digital twin control system.The fault parts of the physical subsystem can be replaced by the corresponding parts of the virtual subsystem.Two faults of a real practical system are considered here: one is the sensor fault and the other is the controller fault.

A. Sensor Faults

In this case, it assumes that the sensor of measuring the output of the real plant fails.If a conventional control method is employed, the physical subsystem becomes an open-loop control system, the stability and performance of the system will change significantly, and it may collapse in a bad situation.Here, a sensor-fault tolerant control scheme is presented, as shown in Fig.5.In this scheme, the output of the real plant measured by the failed sensor is replaced by the output of the digital plant.At the same time, the adaptive model tracking scheme may be needed to ensure the difference between the real plant and the digital plant is within a tolerated bound.

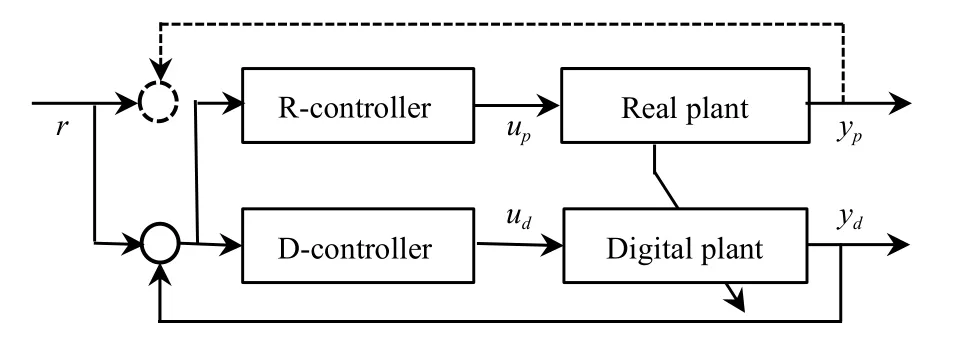
Fig.5.Sensor-fault tolerant control of the real plant.

The outputyp(t) of the real plant is set to be the outputyd(t)of the digital plant in the R-controller, that is

In this way, the real plant is controlled with the support of the virtual subsystem running in parallel so that the stability and performance of the real plant can be maintained within a tolerant range for at least a certain period of time.

B. Controller Faults

In a conventional control system, if the controller of the real plant has a fault, the system has to stop.For example, in the case that the hardware of the controller is damaged or the software of the controller is crashed, the system has to stop.For a practical system, this may lead to enormously economical loss or catastrophe.So, a controller-fault tolerant control scheme for a digital twin control system with a plant controller failure is presented, as shown in Fig.6.

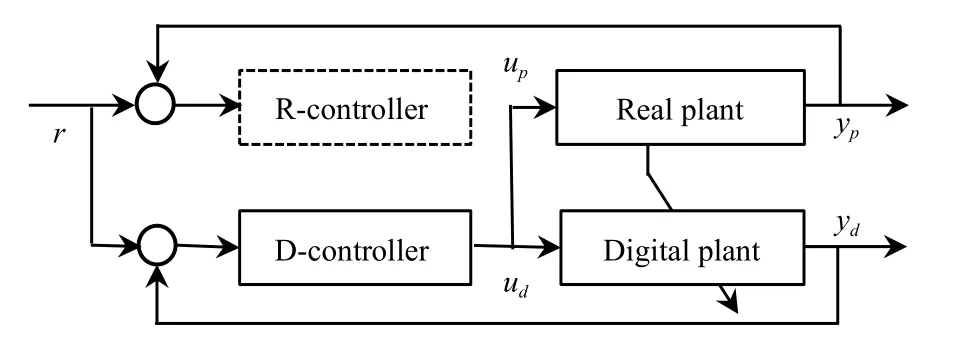
Fig.6.Controller-fault tolerant control of the real plant.

When the R-controller does not work, the control input of the real plant is set to the output of the D-controller, i.e.,

which also leads to similar performance to the sensor-fault tolerant control scheme.

The modelling accuracy of the digital plant is crucial for the fault tolerant control schemes introduced in the two cases above because it will impact the performance of the real plant significantly.Thus, the model tracking scheme plays a very important role in the fault tolerant control of digital twin systems.

VII.STABILITY ANALYSIS OF DIGITAL TWIN SYSTEMS

For the schemes discussed in the previous sections, their closed-loop digital twin control systems are different because the different control schemes are employed.But, the stability analysis procedure of those systems is quite similar.To simplify this procedure, based on the general structure of the digital twin control system proposed in Section II, its stability is discussed here.

The outputs (2) and (4) of the real plant and digital plant lead to

Substituting (48) into the R-controller (7) and (8) results in

and also substituting (49) into the D-controller (9) and (10)yields

Combining the equations of the real plant (1), digital plant(3), R-controller (50) and (51) and D-controller (52) and (53)leads to a high-order nonlinear system

where

Clearly, the stability of the digital twin control system is determined by the closed-loop equation given in (54).Further stability analysis on (54) can be done using nonlinear system methods [40], for example, the nonlinear Lyapunov method.

To demonstrate the performance of the control strategies for digital twin systems proposed in this paper, the following nonlinear plant [41] is considered:

whereyp(t) andup(t) are the output and control input of the real plant, respectively, and the plant parameters areθp,1=0.5, θp,2=1.5 and θp,3=0.3.In terms of the real plant form in(1) and (2), the nonlinear functionsf(·) andg(·) can be chosen as

where φp=1, which means that the output of the plant is also the state of the plant.

A linear model for the digital plant is introduced to approximate the real plant with basis functions chosen to bexd(t),xd(t-1),ud(t) andud(t-1).The functionsfˆ(·) andgˆ(·) of the digital plant are constructed as

where φd=1 and parametersneed to be estimated.

Using the high-order fully actuated control method [41], the D-controller for the virtual subsystem is designed as

wherehd=1,KdpandKdiare the PI control parameters to be tuned.

Following the D-controller, the R-controller is constructed as:

VIII.EXAMPLES

wherehp=1,KppandKpiare the PI control parameters.

The desired control performance is assumed to be the step response of a standard second-order system with damping

ratio of 0.7 and undamped frequency of 5 rad/s.Thus, the transfer function between the desired outputyr(t) and the reference inputr(t) is

which can be discretised with a sampling period of 0.04 s to be

The reference inputr(t) is assumed to be a square wave signal

The initial conditions of the states, outputs and control inputs of the digital twin control system are zeros.For the real plant with θp=[0.5,1.5,0.3]T, the initial parameters of the digital plant are set to

which are estimated using an offline least squares method.

Employing a PI control tuning method (e.g., the trial-anderror method), a set of controller parameters that achieve the above desired control performance given by (62) with an acceptable error is obtained below:

Here, based on the proposed digital twin control system, the five cases are considered, including adaptive model tracking,performance prediction, performance retention, sensor-fault tolerant control, and controller-fault tolerant control.

Case 1: Adaptive model tracking

Assume the parameters of the real plant change from θp=[0.5,1.5,0.3]T, fort∈[0,100) to θp=[0.8,0.7,0.5]T, fort∈[100,200].

The digital plant is redescribed by

where

The adaptive model tracking scheme in Section III is applied to the digital twin control system in Fig.1.The parameters θdof the digital model are recursively estimated online by (29) and (30) with λθ=0.95 andTΘ(-2)=106I.The output responses of the physical subsystem with controller(58) and (59) and virtual subsystem with controller (60) and(61) are almost the same, as shown in Fig.7, where the parameters used in the digital plant, the R-controller and Dcontroller are updated with time but the PI parameters are fixed as in (63).The parameter estimation of the digital plant is shown in Fig.8.Clearly, the adaptive model tracking scheme performs well even if the parameters of the real plant vary more than 50%.

Case 2: Performance prediction

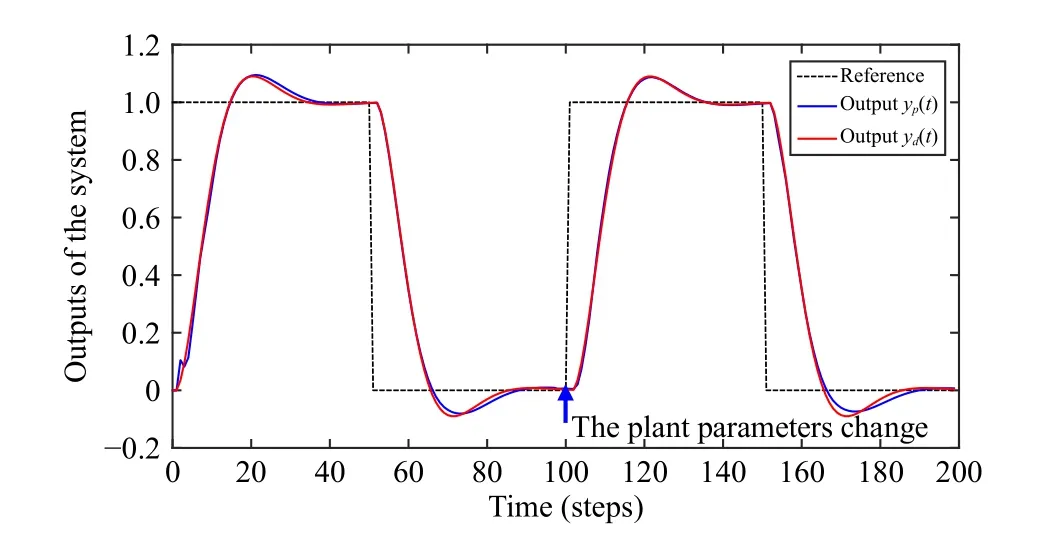
Fig.7.The output responses of the system (Case 1).

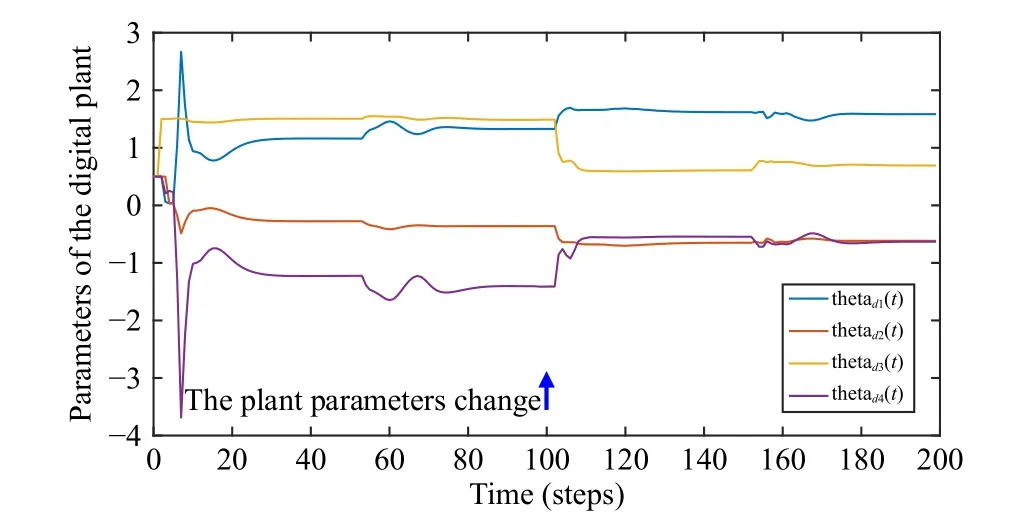
Fig.8.Parameter estimation of the digital plant (Case 1).

In terms of the predictor (33)-(36) introduced in Section IV,the 10-step ahead predictions of the states, output and control input of the data plant are calculated via the virtual subsystem,i.e.,

fori=0,1,...,9, wherexˆd(t|t)=yp(t).

Let θp=[0.5,1.5,0.3]T.The parameters θdof the digital model are estimated using the adaptive tracking scheme in Case 1.The 10th-step ahead output predictions of the digital plant and the output of the real plant with controller (60) and(61) are shown in Fig.9.The control input of the real plant and the control input predictions of the digital plant are given in Fig.10.It is clear that the difference between the output and its prediction is very small except the beginning part (t<10)because the first 10-step output predictions are set to zero.

Case 3: Performance retention

To evaluate the control performance, two simple cost functions are introduced as

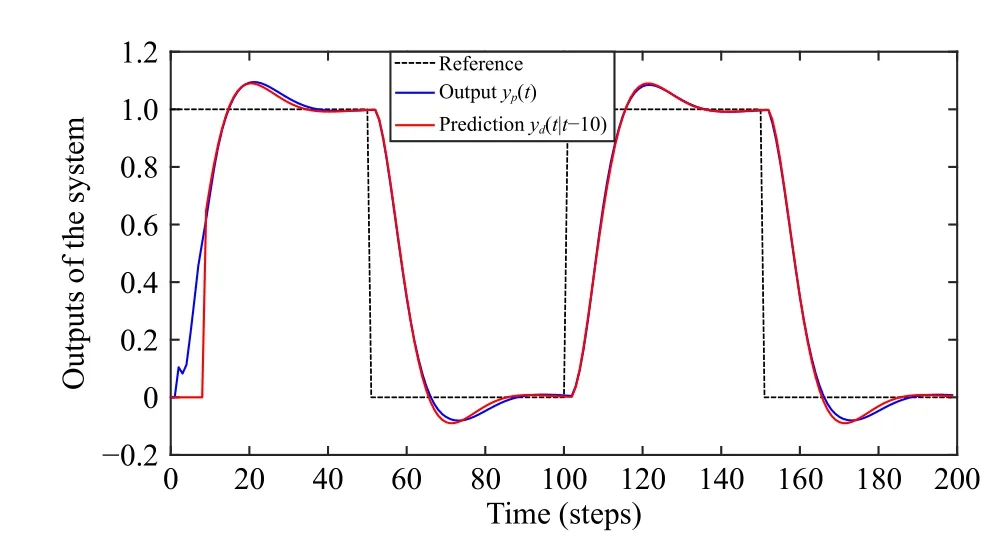
Fig.9.The output responses of the system (Case 2).

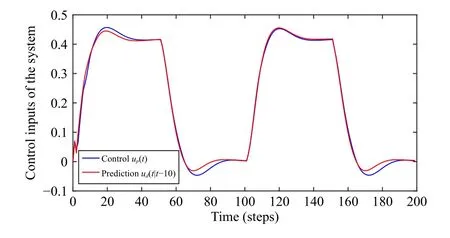
Fig.10.The control inputs of the system (Case 2).

where αp=(Kpp,Kpi) and αd=(Kdp,Kdi) , the desired outputyr(k)is calculated by the desired system (62),Nis a positive integer and should not be less than the settling time of the desired system.Here letN=200, the desired performance and tolerable performance error be

Let the parameters θp=[0.5,1.5,0.3]Tof the real plant be fixed and the parameters of the digital plant be set to[1.3178,-0.3866,1.4238,-1.2606]T.At the beginning, the controller parameters are stillKpp=Kdp=0.75 andKpi=Kdi=0.035.Clearly, the control performance of both the physical and virtual subsystems is significantly different from the desired performance given by (62) beforet=100 , as shown in Fig.11.

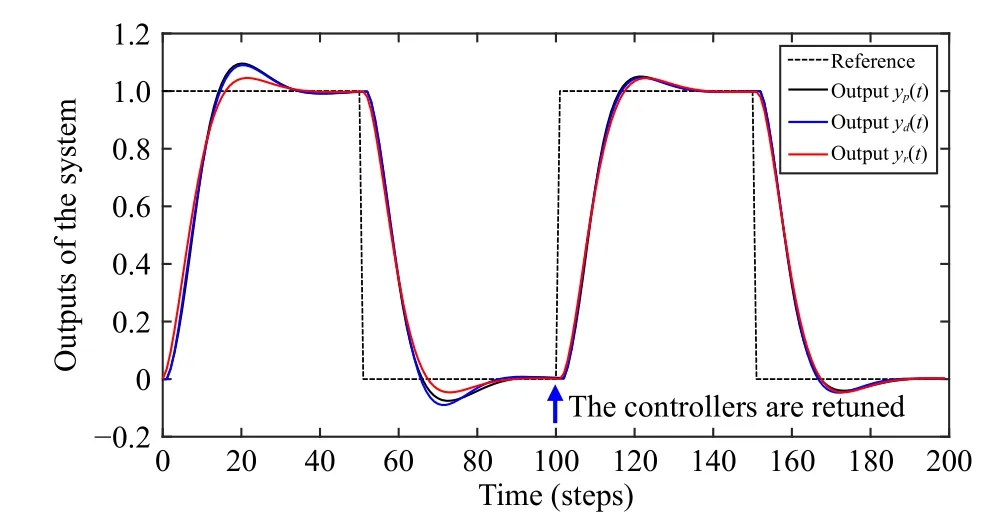
Fig.11.The output responses of the system (Case 3).

Att=100, employing the performance retention scheme in Section V and the genetic-algorithm-based optimization method [38], the parameters of the D-controller are optimally returned to be

so that the performance functionψ1(t,αd) is minimised withψ1(t,α∗d)≤0.0003.At the same time, the parameters of the Rcontroller are updated to be

The control performance is provided in Fig.11.The results show that both the physical subsystem and virtual subsystem have the desired control performance after time att=100.

Case 4: Sensor-fault tolerant control

In this case, the parameters of the real plant are still θp=[0.5,1.5,0.3]T, the parameters θdof the digital model are estimated online using the adaptive model tracking scheme with λθ=0.99.

When the output sensor of the real plant is out of order att=80, letyp(t)=0 in the R-controller.Then, the output of the real plant diverges from the desired outputyr(t) gradually, as shown in Fig.12.If the sensor-fault tolerant control scheme in Section VI is applied, the output of the digital plant replaces the real output in the R-controller (60) and (61), i.e.,

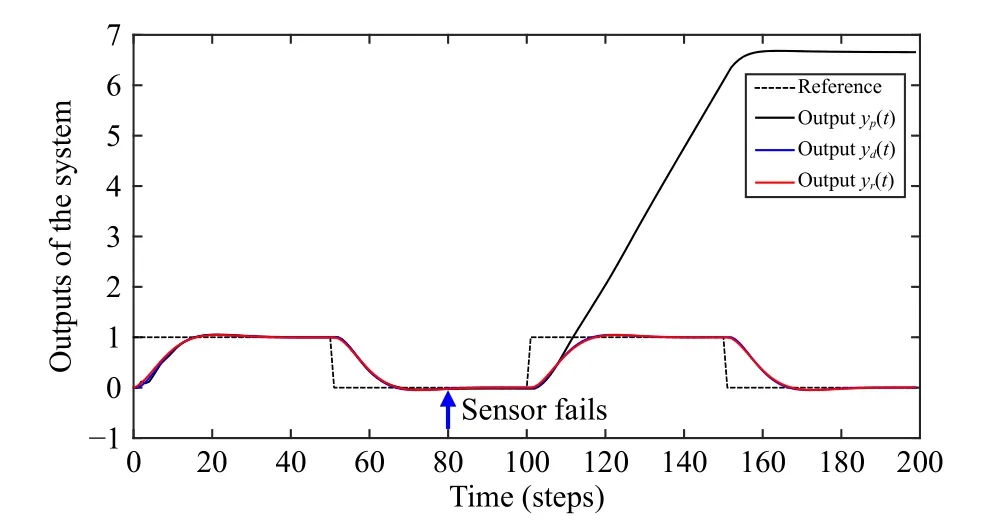
Fig.12.The output responses of the system without sensor-fault tolerant control (Case 4).

The results in Fig.13 illustrate that the control performance of the physical subsystem is still close to the desired one when the output sensor of the real plant fails att=80.

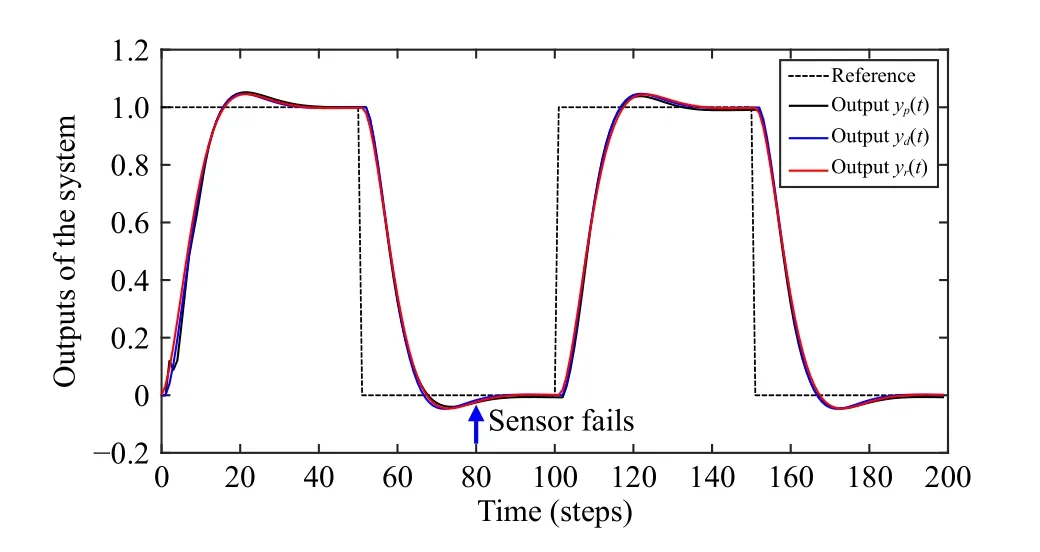
Fig.13.The output responses of the system with sensor-fault tolerant control (Case 4).

Case 5: Controller-fault tolerant control

The system setup is the same as in Case 4.When the R-controller does not work at timet=80, let the output of the Rcontroller be a random signal between -0.5 and 0.5.The physical subsystem collapses immediately, as shown in Fig.14.If the controller-fault tolerant control scheme in Section VI is employed, the output of the D-controller is directly applied to the control input of the real plant, i.e.,

The results in Fig.15 demonstrates that the physical subsystem still follows the desired control performance well after the R-controller failst=80.

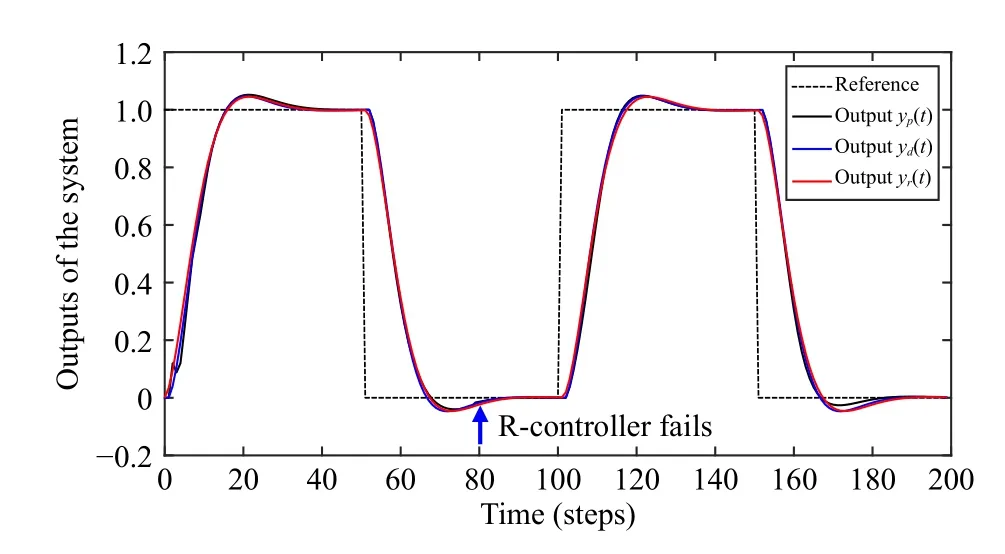
Fig.15.The output responses of the system with controller-fault tolerant control (Case 5).

IX.CONCLUSIONS

This paper has addressed some challenging issues in modelling, prediction and control of digital twin systems.A novel architecture of digital twin control systems has been proposed to provide a fundamental structure for practical applications of digital twins in control systems.To make full use of the advantages of digital twins, several schemes for digital twin control systems have been presented, including adaptive model tracking scheme, performance prediction scheme, performance retention scheme, and fault tolerant control scheme.The adaptive model tracking scheme can track the dynamics variations of real plants in an iterative online estimation way.The performance prediction scheme can predict the future performance of the physical subsystem via the virtual subsystem.The performance pretention scheme can maintain the desired control performance when the dynamics of the real plant varies.The fault tolerant control scheme can cope with a sensor fault and controller fault of the physical subsystem with the support provided by the virtual subsystem.The stability of digital twin control systems has been analysed as well.A number of simulation results have demonstrated the performance of the digital twin control systems with different schemes above.

To put the proposed schemes into practice, more research work on physical experiments and practical applications is needed and will be carried out in the near future.Also, there are other issues that are not discussed in this paper, for example, uncertainties, modelling errors, disturbances and noises,which impact the stability and robustness of a digital twin control system.In addition, compared with other conventional control systems, there are some disadvantages, for example, increased consumption of computing resources and reduced data security.A digital twin control system requires a large number of computing resources, which may become limiting factors in large-scale applications, leading to an increase in computing hardware cost.It involves much system information in the process of data collection and use, and the protection of this information is an important issue in the application of the digital twin control system.Although there still exist a number of challenging issues above, the proposed architecture and schemes have provided fundamental base for further study on digital twin control systems.