驻人月球科研站围护结构传热性能分析
2024-01-26阮昌运张春晓潘文特孟治国叶罕霖
阮昌运,沈 朝,张春晓,潘文特,孟治国,叶罕霖
(1.哈尔滨工业大学 建筑学院,哈尔滨 150090; 2.寒地城乡人居环境科学与技术工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090;3.吉林大学 地球探测科学与技术学院,长春 130026;4.中国空间技术研究院 钱学森空间技术实验室,北京 100094)
驻人月球科研站是人类推动深空探测和资源开发的必经之路[1]。中、美等航天大国均推出月球科研站建设计划,将其作为航天事业发展的空间战略项目。然而,月球存在高强度热震、超高真空、低重力、强辐射等客观环境,给月球科研站的建造和运维带来严峻的挑战。为保障月球科研站中人员的基本生活需求和设备的高效运行,极端条件下的热环境营造成为了重中之重。目前,对于月球科研站的研究主要集中在总体研究方案、科研站选址、结构设计、能源利用等方面,多以提出设想并辅以论述为主,而对月球科研站的冷热负荷计算和围护结构的材料设计等实质性研究较为有限[2-3]。
本研究基于月球表面超常规的太阳辐射和温度波动,结合有限差分法模拟月球科研站围护结构的动态传热过程,并从导热系数、密度、比热容、厚度、表面发射率、室内对流换热系数、朝向等因素探究了驻人月球科研站围护结构的保温隔热性能,为明晰月球科研站围护结构的传热特性以及材料设计提供理论指导。
1 驻人月球科研站选址分析
Staehle等[4]提出了驻人月球科研站选址需优先考虑的四要素分别是战略目标、科学目标、操作约束和资源开发。月球极区区域可获得持续日照,为科研站的能源需求提供保障[5],并且有利于开展永久阴影区的内部勘察和月岩垂直分层研究[6]。但极区有效太阳辐射低,且存在长时间的黑夜情况,不利于月球科研站的长期发展。
月球正面赤道拥有丰富的钛铁,可以用于制氧,从矿产资源利用的角度出发该区域更适合建设月球科研站[7]。Taylor等[8]用克莱门汀数据和月球勘探号数据进行分析,发现在史密斯海处建设月球科研站可以很好地满足科学目标和资源开发。因此,综合考虑选取赤道附近85.8°E、1.7°N地区为科研站选址进行传热性能分析。
2 驻人月球科研站围护结构传热模型
2.1 月表太阳辐射模型
月表太阳辐射研究是建立月球科研站的必经之路,也是深入研究月表温度分布以及能源利用等方面的基础。采用行星/月球精密星历DE430获取日月空间位置信息和天平动的转换角序列,并利用美国海军天文台推荐的NOVAS源代码库,调用历表等文件信息获取各坐标轴下的瞬时天球位置。在不考虑地形的条件下,通过几何方法建立月面太阳辐射模型,如图1所示,计算出的太阳辐射值与角度如图2所示。
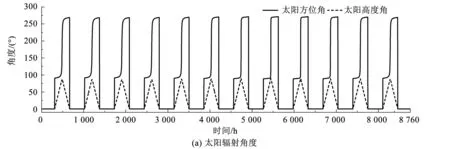
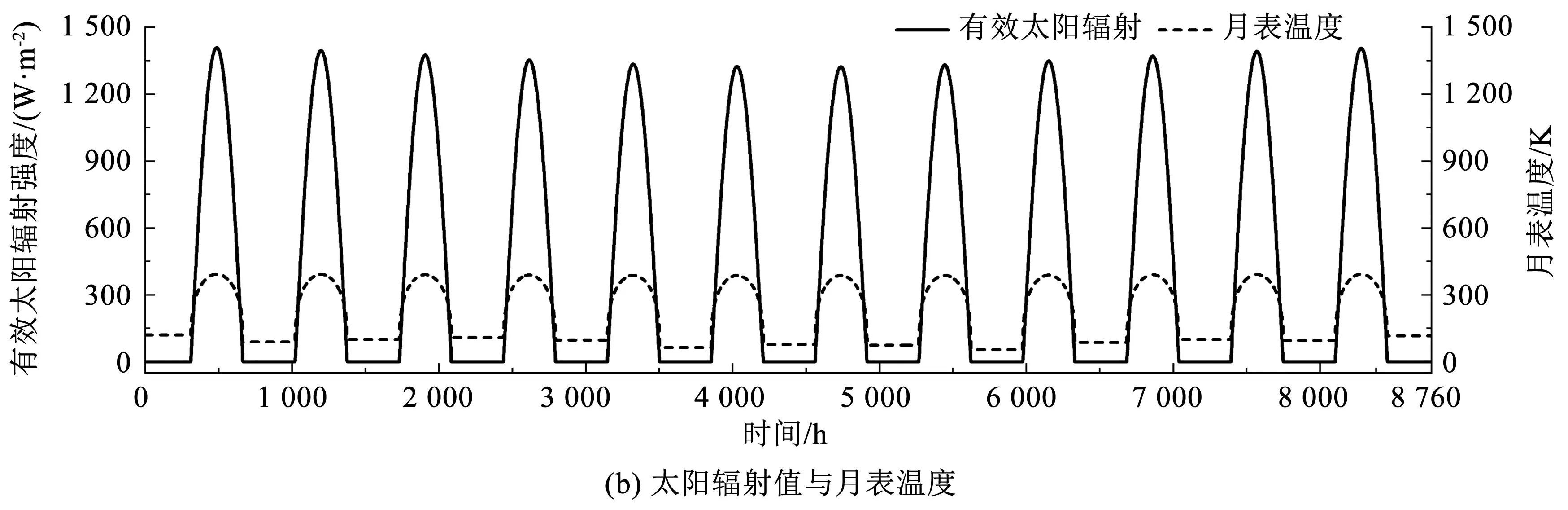
图2 月表太阳辐射情况与温度数值Fig.2 Values of solar radiation and temperature on the lunar surface
月球单位表面的稳态温度可表示为[9]
(1)
式中:S为月表有效太阳辐射值;Q为内部热流,取18 mW/m2;σ为玻尔兹曼常数;ε和α分别为月球表面的发射率和反射率,取0.92和0.127[10]。当太阳辐射为零时,月表温度的取值为日出与日落时温度的极小值,计算出全年月表温度,如图2(b)所示。
2.2 围护结构传热模型
2.2.1 围护结构外表面净辐射换热量计算
如图3所示,围护结构外表面受到太阳直接辐射、太阳散射辐射、地球辐射以及月面长波辐射的作用,其净辐射换热量计算公式为
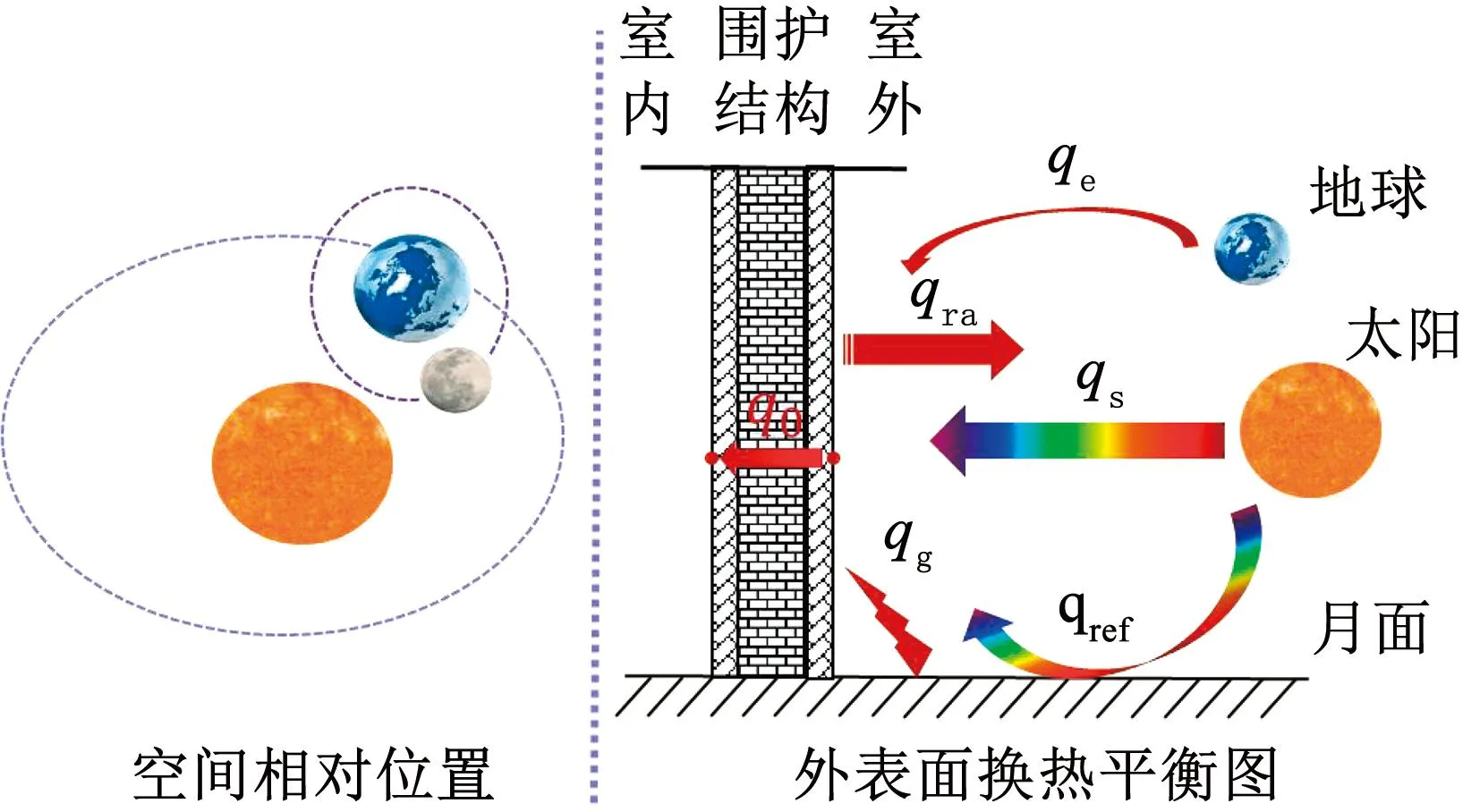
图3 围护结构外表面换热示意Fig.3 Schematic representation of heat transfer on the outer surface of the envelope
q0=(1-α1)(qs+qe+qref+qg)-qra
(2)
式中:α1为围护结构外表面反射率,qs为有效太阳辐射热,qe为有效地球辐射热,qref为太阳辐射散射热,qg为地面长波辐射热,q0为围护结构外表面向室内侧传导的热量,qra为围护结构外表面热辐射量。
有关地球辐射对月面的影响,Song等[11]建立了一维非定常模型,定量计算太阳辐射、地球表面辐射和月球内部热流这3个因素引起的月表温度变化,结果表明,太阳辐射对月表温度变化具有显著的影响,而地球表面辐射引起的变化相对太阳辐射作用较小,因此,在分析月球科研站围护结构的传热时,可忽略地球辐射的影响,即qe=0。
关于月面长波辐射热qg,设其温度值为Tg,月球表面发射率为εg,根据角系数相对性有
φg,1Ag=φ1,gA1
(3)
月球表面对月球科研站外表面的总辐射能量为
(4)
(5)
月球表面的漫反射能量主要包括太阳直射的二次反射和热红外辐射,在计算月球表面的太阳散射热qref时,采用朗伯散射原理[12],可得
qref=αIφ1,g
(6)
式中:α为月球表面半球反射率,I为月球表面太阳辐射热量。
围护结构外表面辐射量遵循斯蒂芬-波兰兹曼定律,取围护结构外表面温度为T1,发射率为ε1,可得
(7)
有效太阳辐射量qs的计算涉及太阳高度角、太阳方位角以及太阳辐射量。为方便计算,建立空间直角坐标系,以所选月球科研站所在位置为原点,正东方向为x轴,正北方向为y轴,科研站所在位置切面外法向方向为z轴(见图4)。
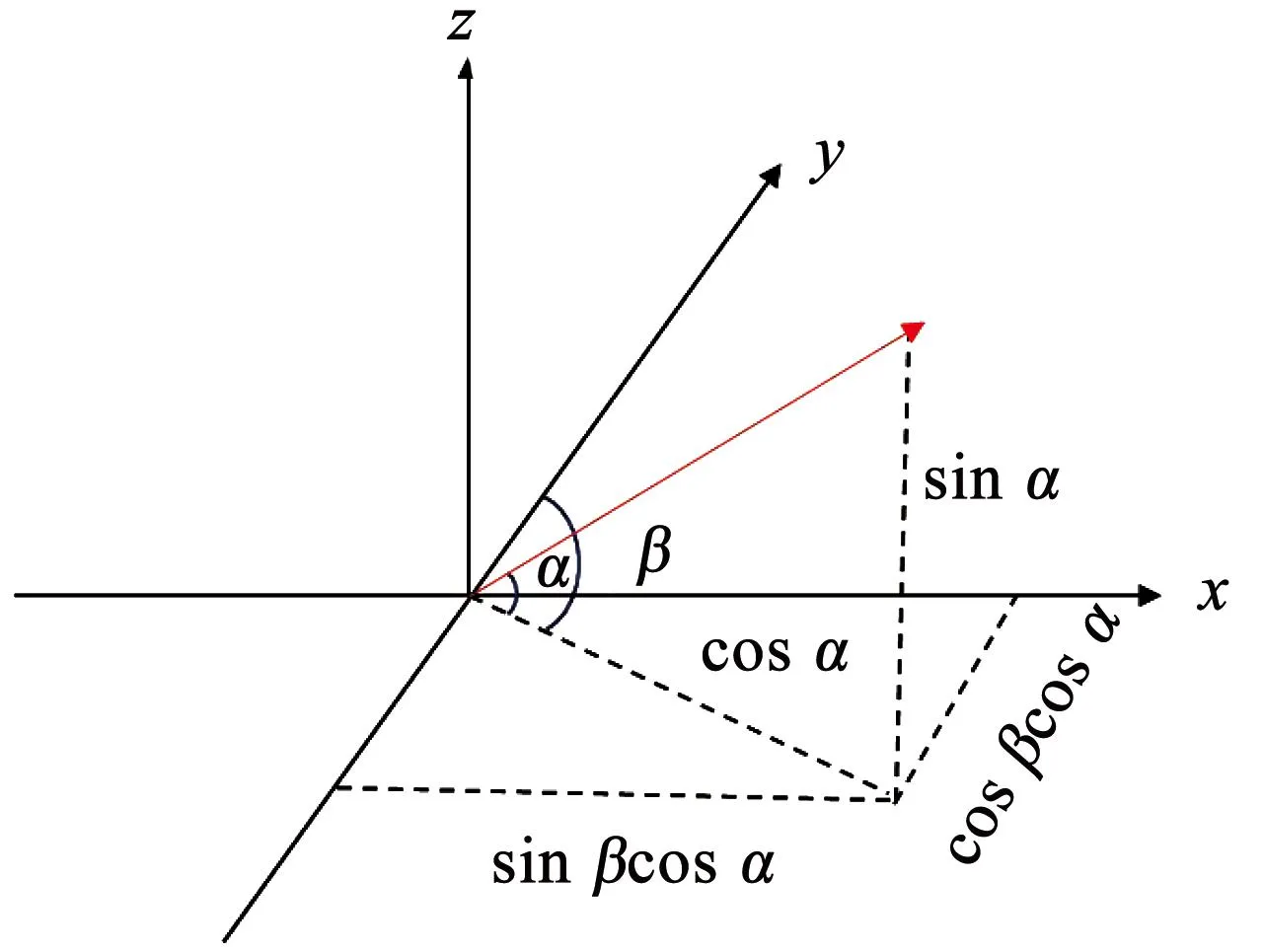
图4 太阳辐射角度关系示意Fig.4 Schematic representation of solar radiation angle
太阳辐射方向向量为
m=(cosαsinβ,cosαcosβ,sinα)
(8)
式中:α为太阳高度角,β为方位角,围护结构的外法向向量n=(a,b,c)。
则向量n和m夹角为
(9)
qs=Icosθ
(10)
当cosθ≤0时,围护结构有效太阳辐射qs=0。
2.2.2 差分法计算模型
建立单一围护结构的基本传热方程,首先需要对围护结构进行空间差分,建立各个温度节点的热平衡方程组。由于差分法与DeST所应用的状态空间法在空间上都具有差分的特点,本文计算模型的单一围护结构离散温度节点设置方法与谢晓娜等[13]在DeST计算中所使用的一致,如图5所示。在空间上将多层材料组成的单一围护结构划分为n层,从而确保每层物性均匀,共有n+1个温度节点,其中,t1和tn+1分别为内外表面温度节点。图中虚线将每层平均分为两个半层,分属于不同的温度节点控制。
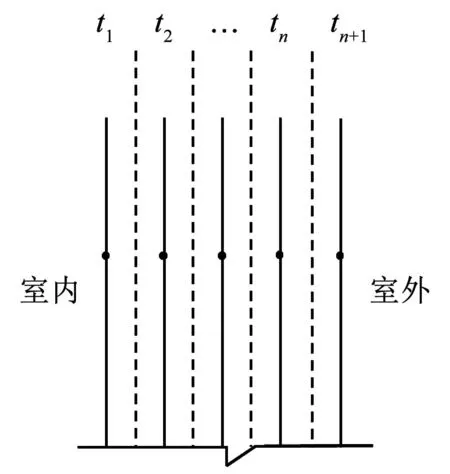
图5 围护结构离散温度节点示意Fig.5 Schematic representation of discrete temperature nodes of the envelope
于是内表面温度节点、内部温度节点、外表面温度节点的热平衡方程为
(11)
(12)
(13)
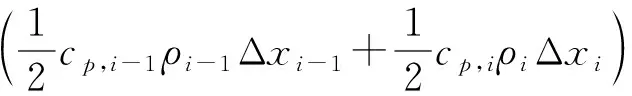
2.2.3 模型验证
EnergyPlus是一款基于BLAST和DOE-2基础上开发的建筑能耗模拟软件,在集成原有优势的基础上开发许多新的功能,广泛运用于建筑能源消耗的全面模拟和经济分析。
为验证差分法计算模型的准确性,在哈尔滨市针对六边形建筑模型,使用EnergyPlus进行对比验证[14]。该模型上下平面由正六边形组成(见图6),边长分别为1.5、5 m,立面高2.5 m,斜面倾角为30°,在间隔的3个立面分别设有1.5 m×2.5 m的门,结构参数如图7所示,地面采用40 mm XPS板铺设。内部边界条件设置时,将室内空气温度设置为20 ℃,人员密度、照明密度、设备密度等内扰量均设置为0,并不考虑新风量带来的影响;外部边界条件使用EnergyPlus官方网站提供的典型气象参数。使用差分法的地面传热计算采用邹平华等[15]推荐的地面当量传热系数。
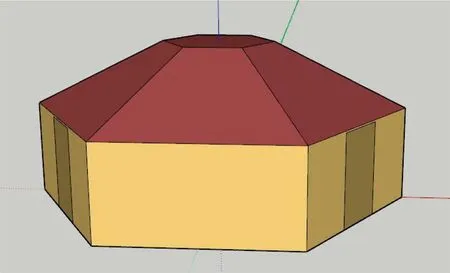
图6 EnergyPlus负荷计算模型Fig.6 Heating/cooling load calculation model (used in EnergyPlus)
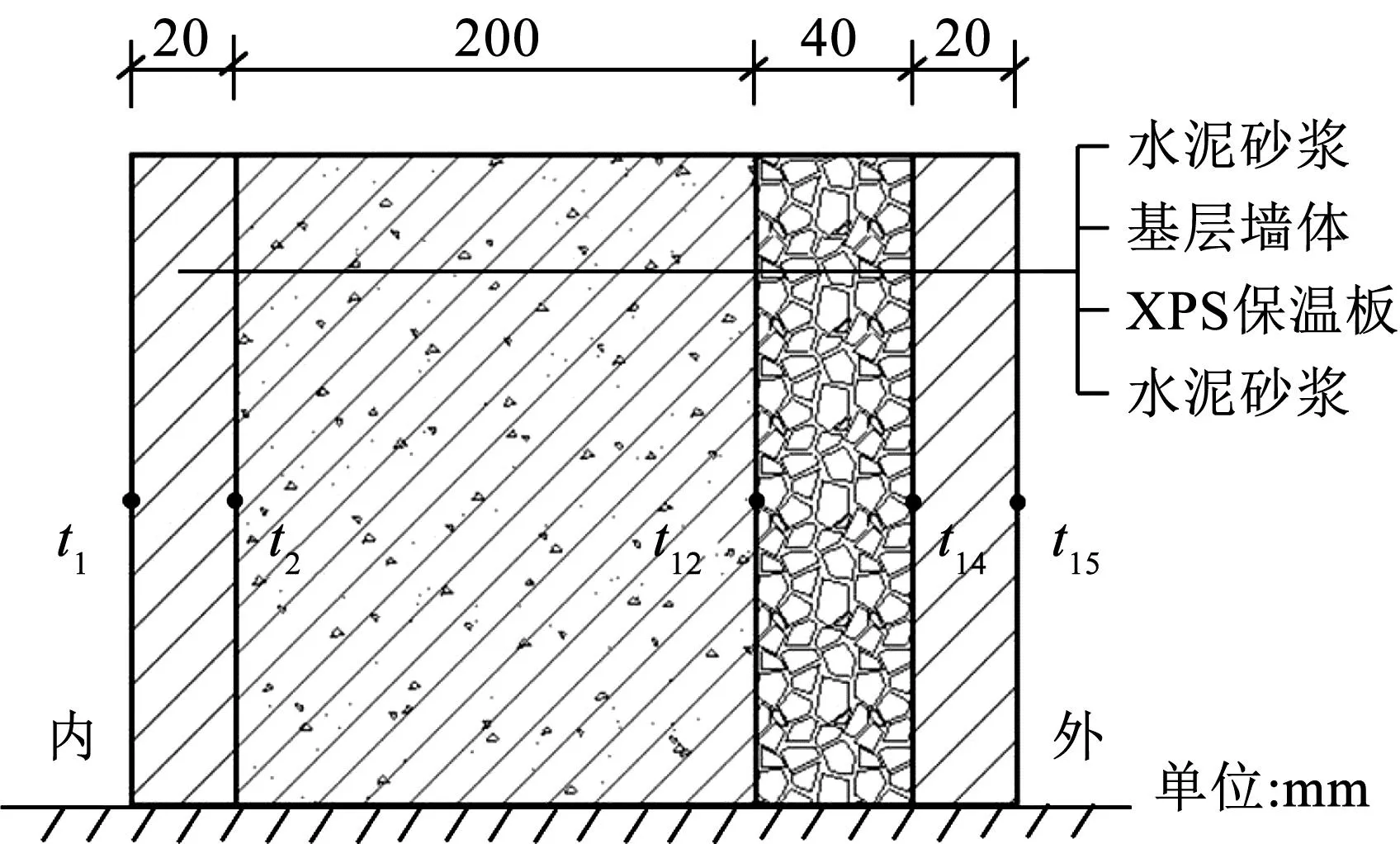
图7 围护结构材料示意Fig.7 Schematic representation of envelope material
计算2005年(典型气象年)1月1日1点—4月30日24点的逐时热负荷,负荷结果对比表明,两种计算方法在1月和4月负荷的平均相对误差为2.9%,2月和3月EnergyPlus计算结果略大于差分法计算结果。EnergyPlus在负荷计算时采用房间热平衡法,假定各个房间空气和围护结构温度分别一致,列出包括室内热扰换热量、围护结构对流换热量、新风渗透换热量、空气混合换热量与空气蓄热量之间的平衡关系式,从而计算分析整个房间的热特性。其次,EnergyPlus在围护结构的热平衡中使用的是CFT模块,其计算最基本的方法是状态空间法,特点是可直接求积分形式的解,且解的稳定性与误差和时间步长无关。不同的是,差分法将墙体传热简化成一维问题,视室内温度为单一节点,对围护结构进行时间与空间尺度的差分,从而保持各节点温度在时间上的连续,进而分析各节点传热特性。如图8所示,两种计算方法在趋势上大致相同,数值上由于计算方法的差异存在微小偏差,因此,差分法可用于月球科研站围护结构的传热特性分析。
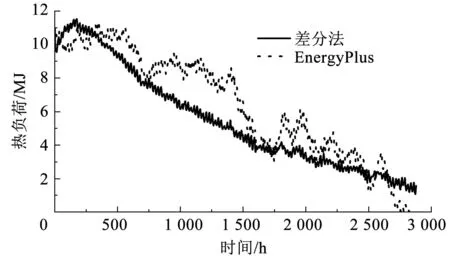
图8 负荷计算结果对比Fig.8 Chart for comparing load calculation results
3 计算结果与分析
对于驻人月球科研站围护结构的热防护设计,可以分为防热层、隔热层和阻气层,如图9所示。根据美国航空航天局PAIDAE项目的实验结果[16],选取表1所示的材料作为围护结构研究对象。
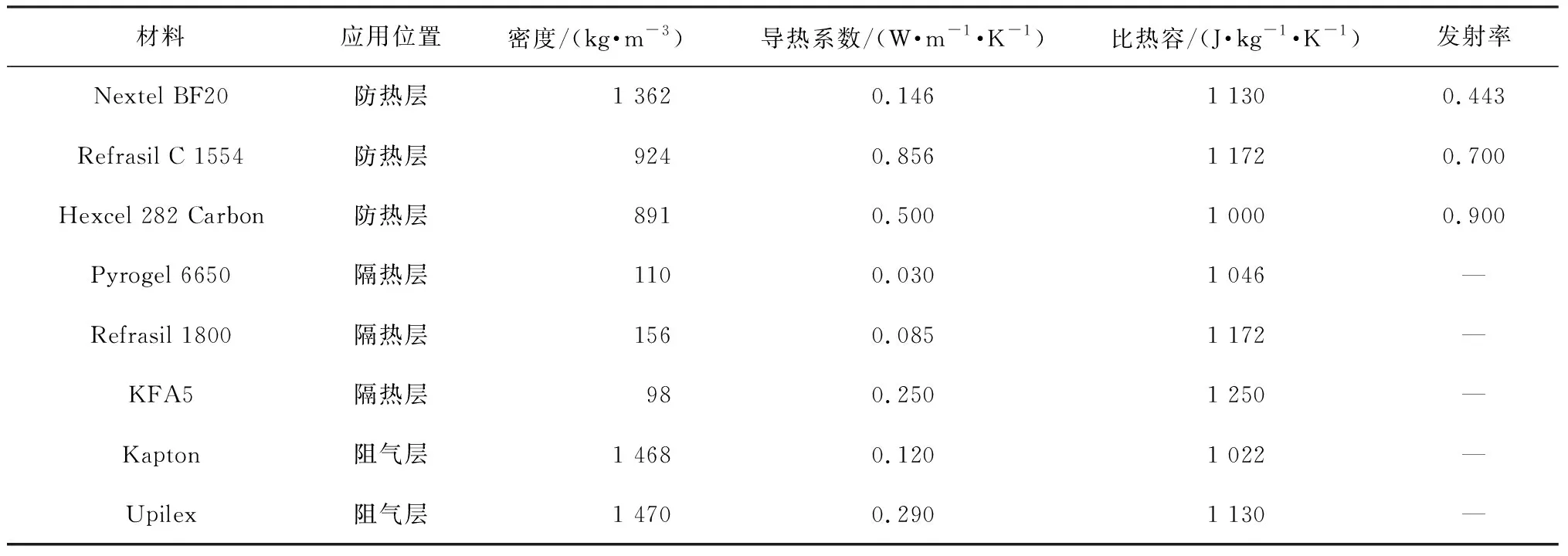
表1 材料参数Tab.1 Material parameters

图9 热防护结构示意Fig.9 Schematic representation of thermal protection structure
在计算月球科研站的辐射换热时,计算步长取0.5 h,计算总时长为月球两天(约地球两个月),以水平屋顶为基础研究对象。为保障人体的基本热舒适要求,围护结构内表面温度与室内空气温度的差值应小于3 ℃[17],因此,在营造室内20 ℃的默认温度条件下,将表征基本热舒适的内表面温度作为主要研究参数。
3.1 材料物性参数对内表面温度的影响
内表面对流换热系数h取5 W/(m2·K)时,各离散节点温度变化如图10所示。内表面温度t1与外表面温度t6变化存在一定的延迟与衰减,极大值由122 ℃衰减为22.4 ℃,而极小值由-114.6 ℃增加到16.8 ℃,时间均延迟13.5 h,且出现温度衰减的部位主要在隔热层,说明隔热层的材料性能占主导地位。
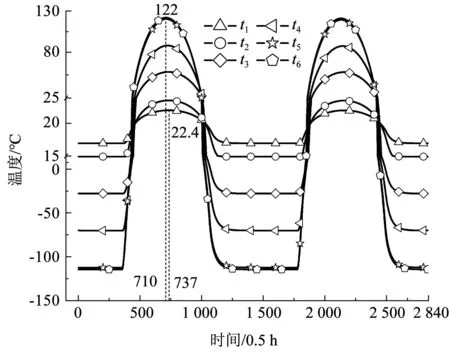
图10 围护结构各层温度变化Fig.10 Changes in the temperature of different layers of the envelope
由于该结构基本可满足人体热舒适要求,以图9中结构为基础,对各层厚度、导热系数等值进行倍率缩放,进而明晰各参数对内表面温度的影响。
增加围护结构的厚度是提高保温隔热性能最常用的方式之一,为增强月球科研站抵御外界环境变化的能力,对防热层、隔热层和阻气层厚度分别为20、240、20 mm的围护结构进行倍率放大,图11为厚度不同时围护结构的隔热情况。随着厚度的增加,内表面温度的波幅逐渐减小,延迟效果更加明显,且变化趋势逐渐变为正弦波动形式。当厚度增加到5倍时,内表面温度的极值分别为20.1、19.5 ℃,较1.0倍厚度时延迟217.5 h,所以,增加厚度可强化保温隔热效果。随着厚度的增加,科研站围护结构的重量也不断增加,导致其发射成本与建造成本直线上升。
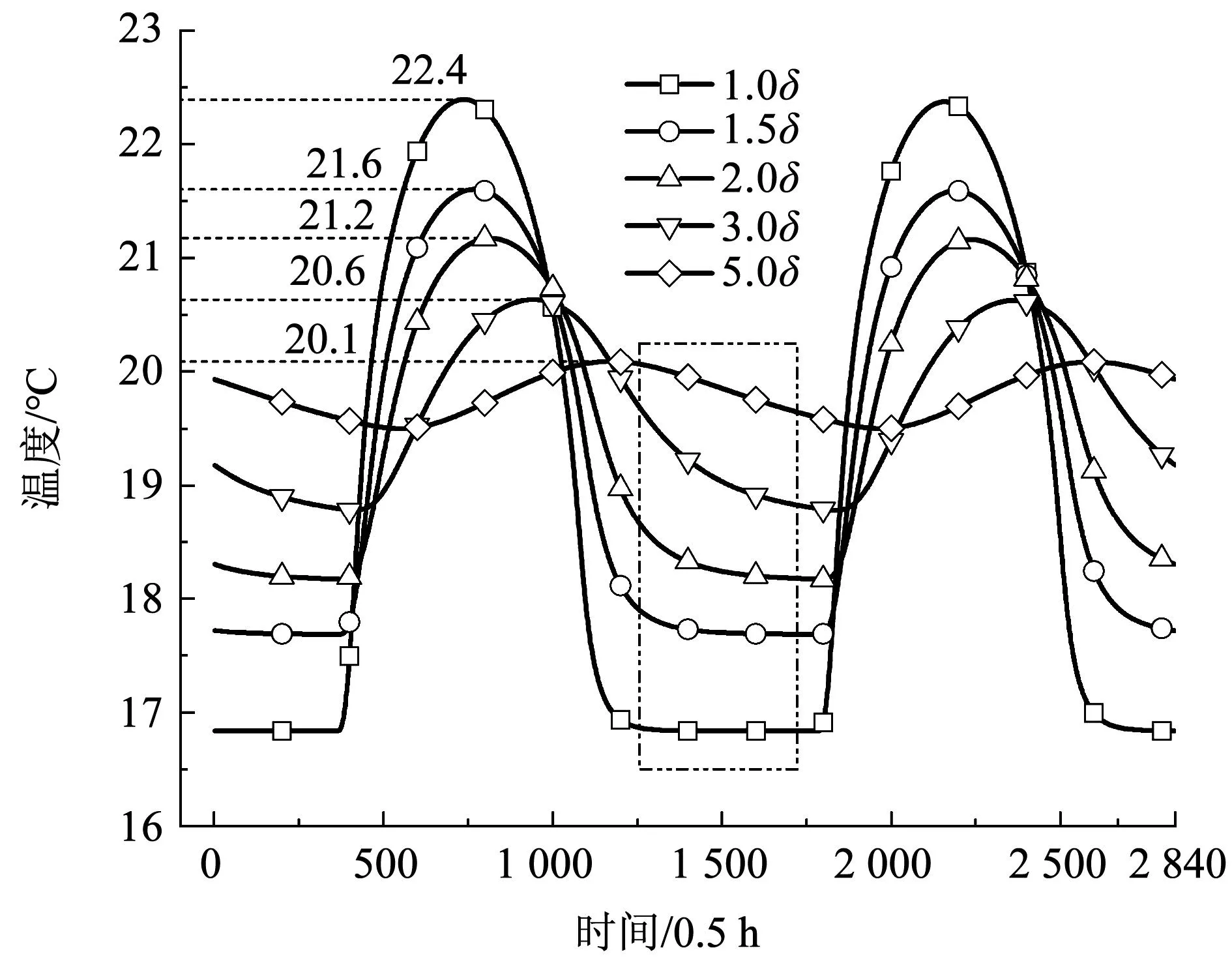
图11 不同厚度时内表面温度变化Fig.11 Changes in the temperature of inner surface with different thicknesses
图12为改变P(P=cρ)时内表面温度变化。随着P的增大,围护结构的热惰性变强,温度波幅也逐渐减小,延迟时间增大,但其与图11相比变化效果较弱。另外如图中阴影区所示,随着P的不断增大,内表面温度的变化率也逐渐减小,对室温的影响逐渐削弱。上述结果表明,P的增大提高了围护结构的隔热效果,但是材料密度的增大提高建造的经济成本,因此,月球科研站的围护结构可选择低密度、高比热的材料。
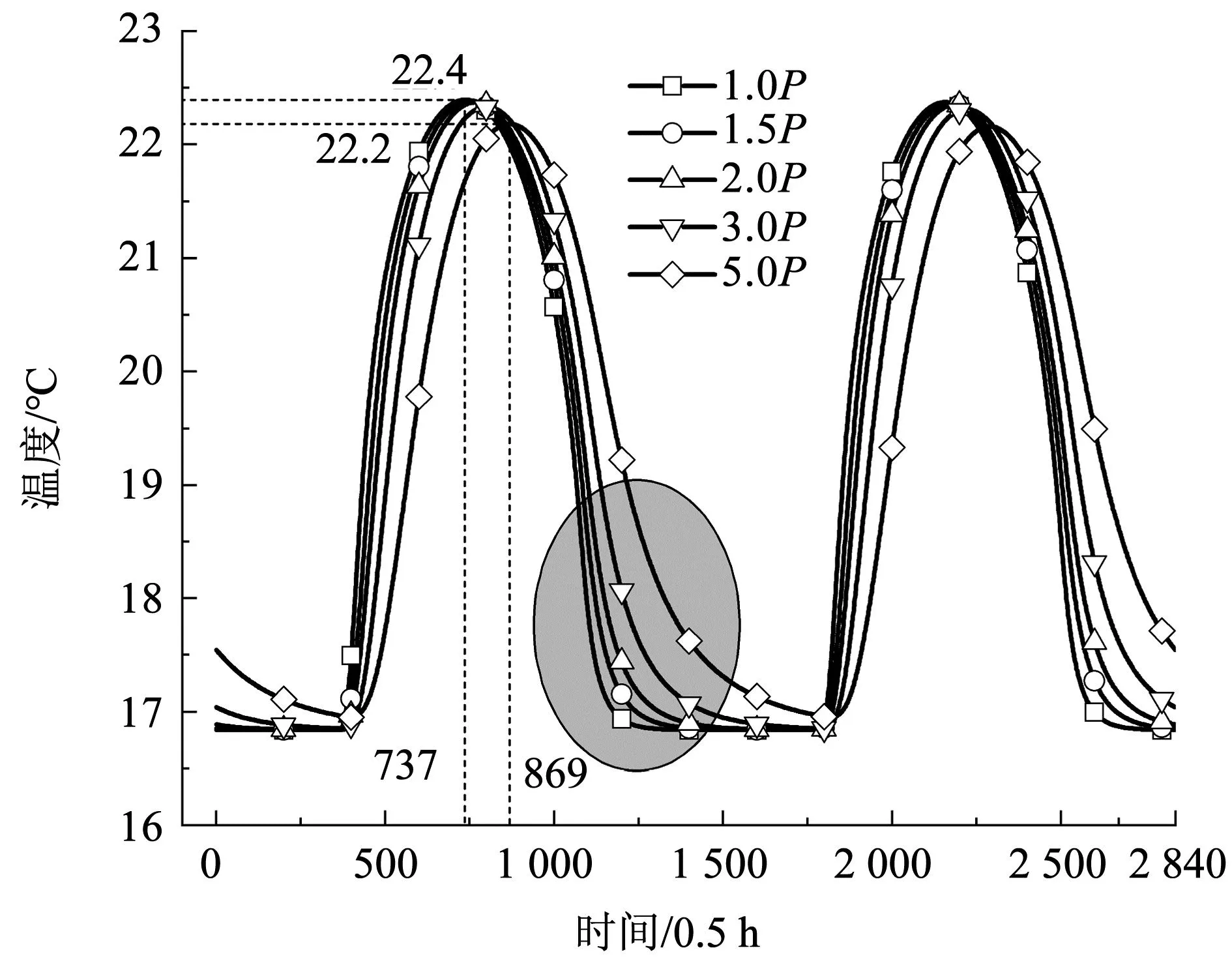
图12 不同P时内表面温度变化Fig.12 Changes in the temperature of inner surface with different P values
图13为导热系数λ影响下表面温度的变化。随着导热系数的降低,对温度削减的效果越明显,同时存在一定的延迟效果。当导热系数降低到0.10λ时,温度峰值由22.4 ℃降低为20.2 ℃,且峰值时间延迟了105 h,夜间的内表面温度提升到19.6 ℃,说明围护结构的隔热性能显著提升。因此,降低围护结构各层导热系数,有利于提高月球科研站的保温性能。
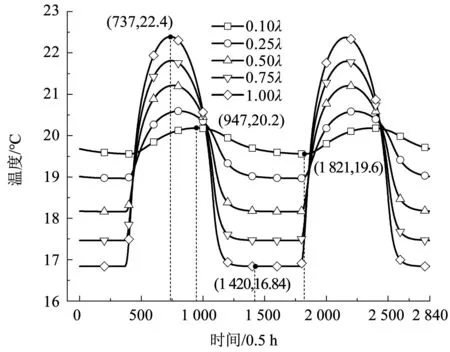
图13 不同λ时内表面温度变化Fig.13 Changes in the temperature of inner surface with different λ values
月球的特殊环境导致月球科研站的内外表面具有不同的传热方式。室内侧以对流换热为主导,因此,探究对流换热系数的影响尤为重要。如图14所示,随着室内侧对流换热系数的增加,内表面温度的波幅逐渐降低,室内温度对于围护结构的传热影响加剧。但是对流换热系数的增加和表面温差的降低对换热量有着相反的影响,理论上存在一个最优对流换热系数,使得内表面与室内之间的换热量最小。
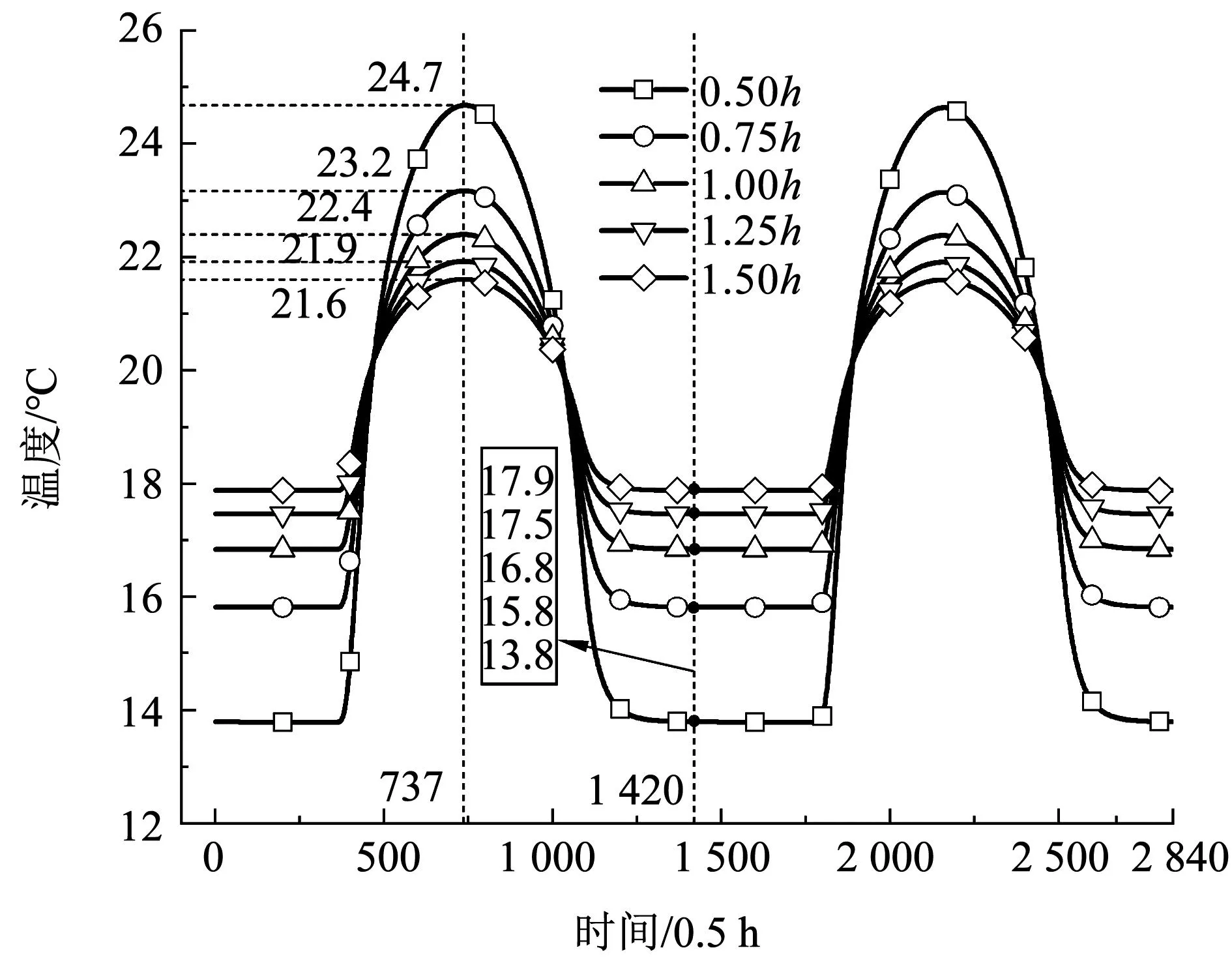
图14 不同对流换热系数时内表面温度变化Fig.14 Changes in the temperature of inner surface with different convective heat transfer coefficients
由于月球环境几乎不存在大气层,科研站外表面主要以辐射的形式参与换热,其反射率与发射率对于月球科研站的能耗具有显著影响。如图15所示,发射率的改变主要影响月球科研站夜间的能量发射,而月昼期间影响很小,主要是受太阳辐射的影响;当发射率降低到0.050时,月昼期间的内表面温度有较明显的延迟与降低。因此,为减少夜间月球科研站的能量损失,应尽量降低外表面的发射率。
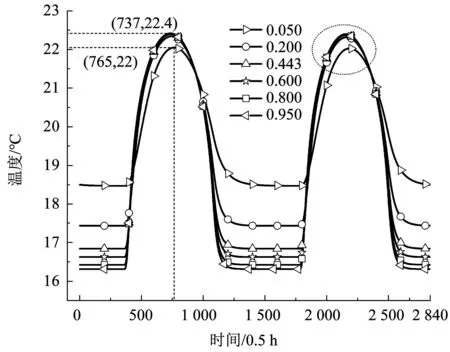
图15 不同发射率时内表面温度变化Fig.15 Changes in the temperature of inner surface with different emissivity
3.2 不同朝向对内表面温度的影响
为探究不同朝向带来的辐射差异影响,固定围护结构的材料参数,分别以水平面屋顶、东西南北立面作为研究对象。如图16所示,各朝向内表面温度在夜间大致相同,受月面热辐射的影响较小。由于位于赤道附近,南北立面所受辐射情况大致相同,且在月球日上午时,东立面受到太阳辐射最强,内表面温度快速升高到22.7 ℃;由于月球表面热辐射与地表反射的耦合作用,表面温度峰值大于屋顶峰值22.4 ℃。在月球日下午时,太阳辐射主要位于西立面,因此,西立面温度升高,其余朝向接收的太阳辐射量降低,内表面温度也相应降低。在设计围护结构时,应增加屋顶与东西立面的保温措施,达到“降峰”的效果,并减少夜间的热量散失;而南北立面应主要考虑夜间的辐射散热,可通过调整发射率降低围护结构的建造成本。
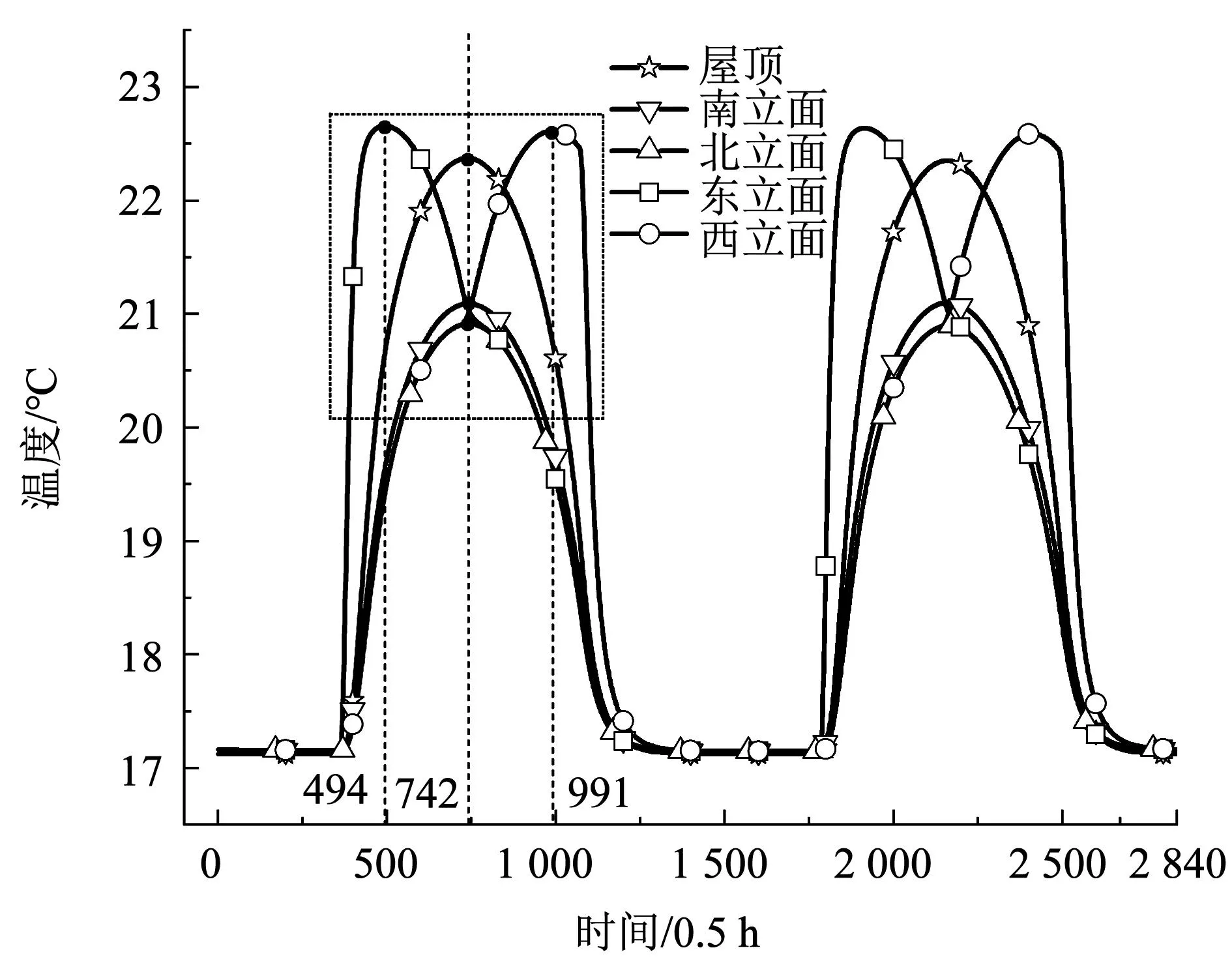
图16 不同朝向时内表面温度变化Fig.16 Changes in the temperature of inner surface with different orientations
3.3 不同材料组合的内表面温度变化
为综合探究材料参数与外表面发射率对内表面温度的影响,选取如表2所示的5个组合。热惰性指标(D)表示受到波动热作用时,材料层抵抗温度波动的能力,其数值越大,表明保温隔热性能越强。计算公式为

表2 围护结构材料组合Tab.2 Combination of building envelope materials
(14)
式中:R为材料层热阻,S为材料层蓄热系数,λ为导热系数,T为温度波动周期(h),δ为材料层厚度。
由图17可知,当外表面发射率一致时,热惰性指标越大,内表面温度的波幅越小,延迟时间越长,即抵抗温度波动能力越强。可知外表面发射率在一定条件下几乎不影响温度的延迟,热惰性指标越大的组合其延迟情况越明显。组合2的发射率与热惰性指标均大于组合1,组合2的延迟情况大于组合1,但其波幅比组合1大;而对比组合1,组合3的波幅更低,延迟能力更强。由此可知,对于不同的围护结构,应综合考虑围护结构的热惰性和发射率,通过个性化定制方案,设计不同朝向围护结构的最佳性能参数。
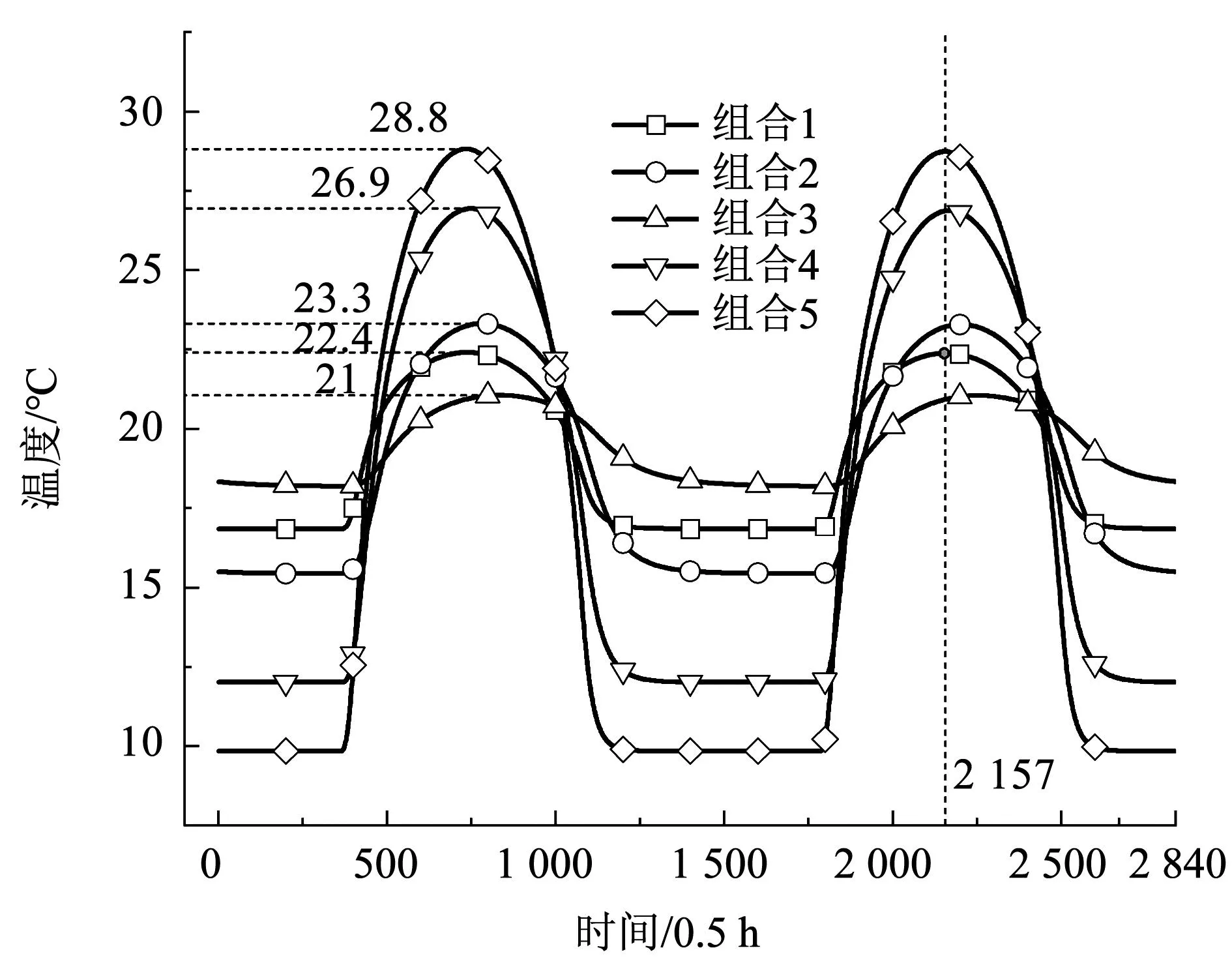
图17 不同材料组合时内表面温度变化Fig.17 Changes in the temperature of inner surface with different material combinations
4 结 论
1)当防热层(Nextel BF-20)、隔热层(Pyrogel 6650)、阻气层(Kapton)厚度分别取20、240、20 mm时,水平屋顶内表面温度极值分别为22.4、16.8 ℃,可满足人体基本热舒适要求。
2)厚度和导热系数对围护结构传热性能影响最为显著。当厚度增加1倍时,极值温度由22.4 ℃降到21.2 ℃,但其建造成本也加倍,可通过增加密度较小的隔热层厚度以及降低导热系数来提高保温性能。
3)存在一个最佳对流换热系数,使得其与室内换热温差所决定的换热量最小。当对流换热系数由0.5倍增加到1.5倍时,极值温度由24.7 ℃降到21.6 ℃。应充分考虑换热量和热舒适要求确定对流换热系数。
4)围护结构的外表面发射率主要决定夜间的散热量,对于白天的内表面温度影响较小。当发射率由0.95降低到0.2时,白天的峰值变化很小,而夜间的温度由16.3 ℃增加到17.4 ℃。
5)综合考虑保温特性与建造成本,可根据不同朝向的辐射特点个性化定制具有差异化热惰性和外表面发射率的材料。
