非高斯脉冲干扰下MIMO 系统频谱智能感知方法

张俊林 刘明骞 张晓波

随着电磁用频设备数量呈现爆炸式增长,频谱资源与频谱资源需求之间的矛盾加剧[1].认知无线电技术利用动态频谱接入技术可以有效利用空闲频谱资源,从而提升频谱资源利用率[2].在认知无线电网络中,为了防止对授权用户产生干扰,认知用户接入频谱时需要准确判断频谱状态,即频谱感知.频谱感知也是电磁频谱战及电磁频谱管控的关键支撑技术[3].随着便携无线终端广泛应用及深度网络的快速发展,协作智能频谱感知以及群体智能频谱感知备受关注.智能化频谱感知为认知无线电网络向实时、精准、高效的智能模型发展提供机遇.

传统的频谱感知方法提取接收信号特征信息有限,且对非高斯脉冲干扰鲁棒性差,研究者们提出了多种有效的改进方法.传统频谱感知方法大致可以分为: 匹配滤波方法、能量检测方法、基于循环平稳特性的方法、基于似然假设的方法以及基于特征值的方法[1].匹配滤波虽然可以获得最佳感知性能,但需要已知主用户信号分布特性.能量检测方法计算复杂度较低,但其检测性能依赖于噪声功率.基于循环平稳特性的方法具有较高的检测概率,但运算复杂度高.基于似然假设的方法也可获得良好检测性能,但该方法通常需要精确的信道参数以及信号和噪声分布.基于特征值的方法可以在缺乏先验信息的条件下获得良好的检测性能[1].

针对非高斯脉冲干扰下的频谱感知,已经出现了多种改进方法.文献[4]提出了基于广义协变系数绝对值和基于多种滤波的频谱感知方法.两种方法有效实现对称alpha 稳定噪声下的信号检测,但算法复杂度较高.文献[5]提出了基于分数低阶矩的频谱感知方法.该方法运算复杂度较低,但对分数低阶指数依赖性较强.文献[6]为了提升圆对称非高斯噪声下的频谱感知性能,提出了一种基于自适应p 范数的检测方法.该方法需要自适应选取参数,导致较高的运算复杂度.文献[7]采用极性符合阵列设计频谱感知方法,但这类方法的性能受条件参数的影响.文献[8]通过利用核函数设计基于核能量的检测方法.该方法具有较高的检测概率,但其计算复杂度也较高.文献[9]利用双曲正切函数设计类似能量检测器.该方法在非高斯噪声和高斯噪声下展现出良好的检测性能.文献[10]利用广义最大相关熵构建检测方法用于提升脉冲噪声环境下的检测性能.

随着深度学习的快速演进,其在信号处理领域表现出了强大的能力[11-12].基于深度学习网络的频谱感知方法不断涌现.文献[13]利用卷积神经网络（convolutional neural network,CNN）提取信号深层特征,并且考虑信道的空间和频谱相关性,实现深度协作频谱感知.文献[14]提出一种基于深度自编码器网络的频谱感知方法,该方法利用自动编码器网络自动特征学习,并利用支持向量机对特征向量进行分类.文献[15]通过利用CNN 和长短时记忆（long short term memory,LSTM）网络充分挖掘信号的空间和时间特征,提出了CNN-LSTM 信号检测器.文献[16]利用短时傅立叶变换作为输入特性,并采用深度学习方法设计盲频谱感知方法.该方法充分利用信号的时频域信息,获得良好的检测性能.文献[17]以协方差矩阵作为输入特征,提出了一种基于CNN 的检测方案.文献[18]利用卷积神经网络提取协方差矩阵深层信息,并依据二元假设模型设计检测统计量和检测门限进行信号检测.文献[19] 提出了一种无监督智能频谱感知方法,该方法利用变分自动编码器提取信号特征,并依据深度聚类网络进行无监督分类检测.文献[20]将捷径连接引入传统CNN 频谱感知网络,从而提升CNN 频谱感知方法的检测性能.文献[21]提出了一种基于密集残差网络的频谱感知方法,该方法将密集链接引入CNN 网络,有效提高网络提取特征的能力,进而提升了信号检测准确率.

基于以上分析,面向非高斯脉冲干扰和高斯噪声共存环境下的频谱感知问题,提出一种协作频谱智能感知方法.与现有方法不同,该方法利用广义协方差矩阵表征信号统计特性,并通过构建基于Transformer 的自注意力机制频谱感知模型充分挖掘信号深层特征,进而利用假设检测实现MIMO频谱感知.

1 系统模型

考虑一种多主用户和多天线认知用户构成的MIMO 频谱感知场景.主用户数目为P,认知用户接收天线数目为M.假设主用户信号在频谱感知期间可以持续出现,且认知用户可以及时接收到主用户信号.认知用户第m 根天线的接收信号可以表示为

其中,sp表示第p 个主用户发射信号,hmp表示第p个主用户和认知用户第m 根天线间的衰落信道,wm（n）表示加性高斯白噪声,Im（n）表示非高斯脉冲干扰.认知用户接收信号的矩阵形式表示为

其中,H 为平坦衰落信道矩阵,s（n）为发射信号矩阵,W（n）表示加性高斯白噪声矩阵,I（n）为非高斯脉冲干扰矩阵.

多天线频谱感知问题建模为二元假设检验问题:

其中,H0表示频谱未被占用,即主用户信号不存在,H1代表频谱被占用,即主用户信号存在.

采用对称alpha 稳定分布（symmetric alpha-stable distributions,SαS）模型刻画非高斯干扰.SαS 通常利用其特征函数进行表征,即:

其中,α 为特征指数,γ 表示分散系数,μ 为位置参数[6].

2 MIMO 系统频谱智能感知方法

2.1 广义协方差矩阵

传统的CNN 频谱感知方案采用接收信号的协方差矩阵或IQ 两路信号作为网络的输入特征,通过利用卷积层、池化层以及全连接层挖掘输入特征的局部深层信息,并利用Softmax 函数的输出构造检测统计量与检测门限.然而非高斯脉冲干扰使得接收信号幅度表现出大幅度脉冲特性,从而破坏协方差矩阵的统计特征.为了应对非高斯脉冲干扰的影响,引入以一种非线性变换器,并构建广义协方差矩阵作为网络的输入.广义协方差矩阵的表达式为

式中,Cim表示为

且rm（n）经过非线性变换器后信号为

根据文献[23],Cmi满足

据此,Cmi在SαS 稳定分布干扰下是有界的.

依据式（5）,Cr可以进一步表示为

式中,Cmi近似表示为

其中,Σqm可以近似表示为

2.2 Transformer 模型

Transformer 网络模型通过引入注意力机制,将编码器-解码器进行堆叠,从而构建Encoder-Decoder并行化架构[24].Transformer 模型通过自注意力来提取到输入数据中全局的特征,可以避免丢失部分局部特征.Transformer 模型的基本结构如图1 所示,其中,编码模块主要是自注意力层和前馈神经网络层构成,且每个子层都进行了残差连接和层归一化处理.

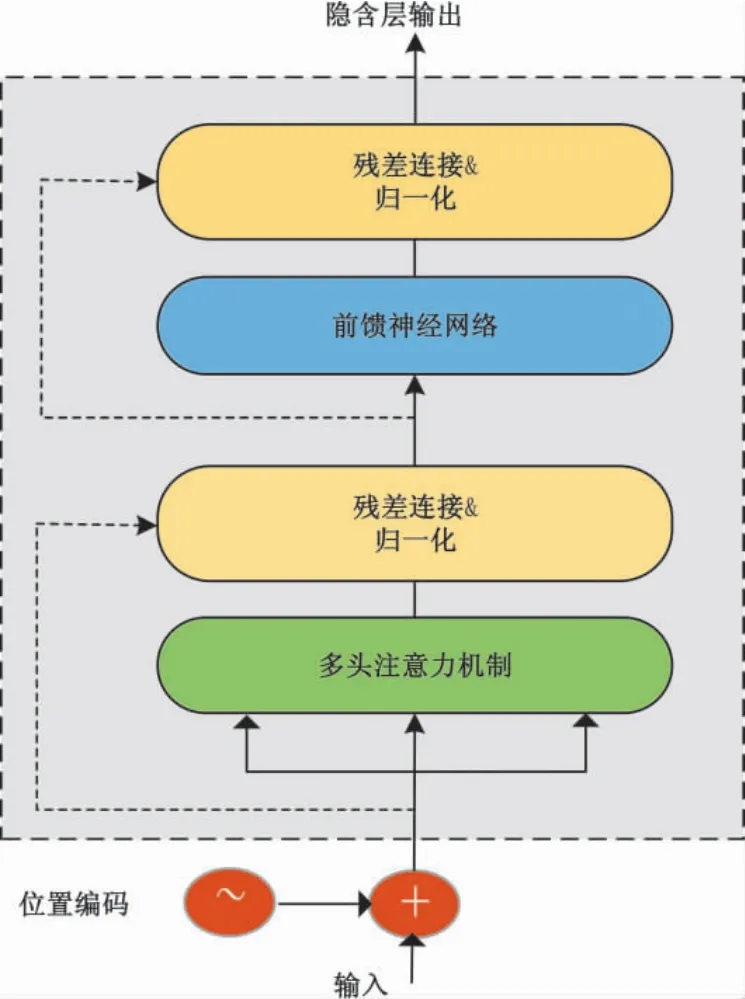
图1 Transformer 模型基本结构Fig.1 The Basic structure of the Transformer model

自注意力机制的引入使得网络可以挖掘输入数据内部相关性信息,进而构建全局依赖关系.缩放点积注意力是应用较为广泛的方法,其计算式为

其中,dk表示Q,K 向量的维度.

Transformer 模型利用多个缩放点积注意力构成多头注意力机制,从而提取更加丰富全面的特征,同时提升自注意力机制的运算速度.图2 为多头注意力机制.多头注意力机制计算式为

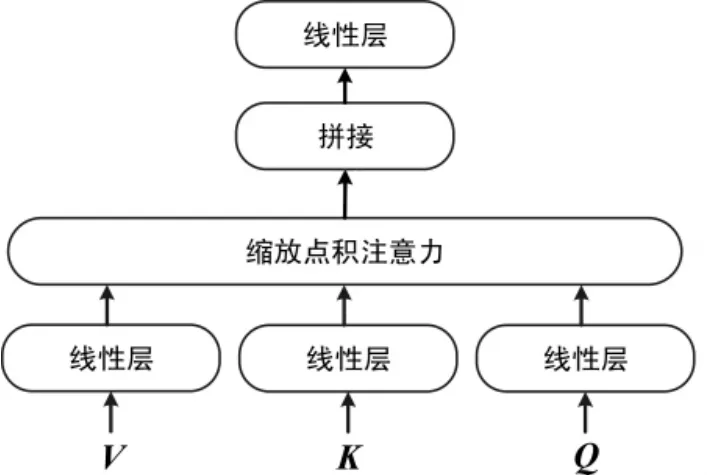
图2 多头注意力Fig.2 Multi-headed attention mechanism

Transformer 模型不具备递归与卷积等操作,导致输入数据的顺序信息丢失,从而无法对数据位置关系进行建模.为了便于利用位置信息,需要在网络中附加位置编码.通常采用正弦和余弦函数来实现位置编码,具体如下:

其中,pos 为位置,i 表示维度,dmodel表示模型维度参数.

2.3 基于Transformer 模型的频谱感知

设计了一种基于Transformer 模型自注意力机制的频谱感知方案,其结构如图3 所示.该网络包括预处理模块,编码模块,全连接层以及Softmax 层.其中,编码模块由4 个Encoder 组成,且每个Encoder 都进行多头自注意力运算.网络流程如下: 预处理模块将输入的广义协方差矩阵切分为块状,并通过线性投影变换,实现块状向量化.为了实现信号检测,需要在Input Embedding 中引入一个可学习的类别词符,并与位置编码构成输入特征矩阵[25].编码模块利用多头注意力结构以及其残差连接、归一化、前馈神经层及其残差连接提取输入向量的深层特征,即从不同的向量子空间中学习不同的特征,提取到更丰富的特征.经过全连接层进行特征映射之后,将全连接层输出的特征分类通过Softmax 层进行概率映射,并输出特征向量.

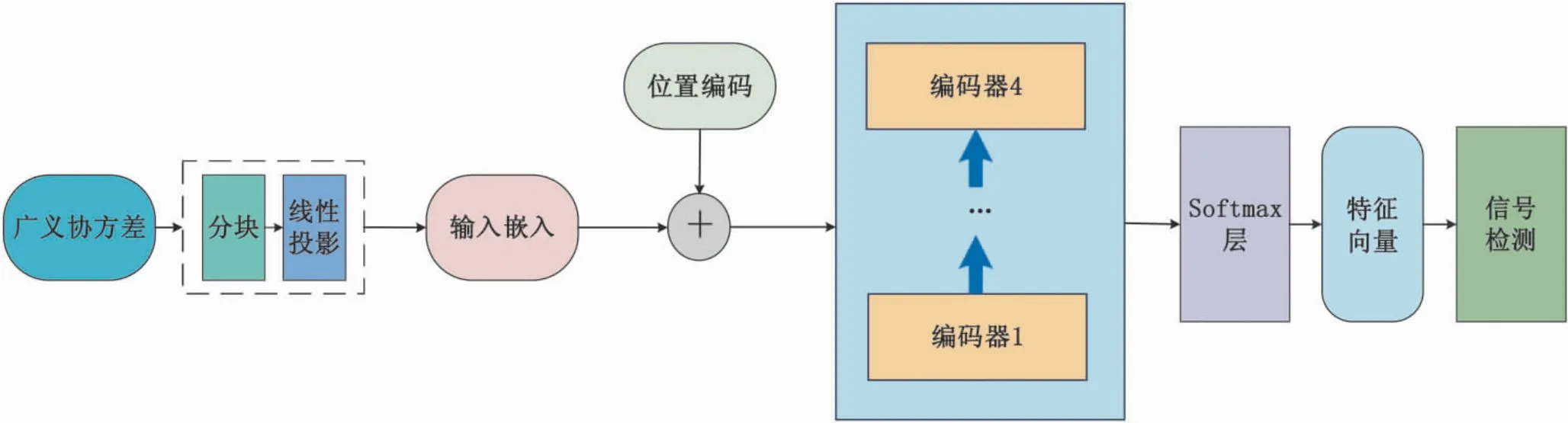
图3 基于Transformer 模型的频谱感知网络Fig.3 Transformer model-based spectrum-sensing network structure

利用反向传播算法调整ω 和b,经过多次循环后得到网络最优参数ω*和b*.在训练阶段,也采用自适应距估计优化算法.模型训练过程中的部分网络参数如表1 所示.

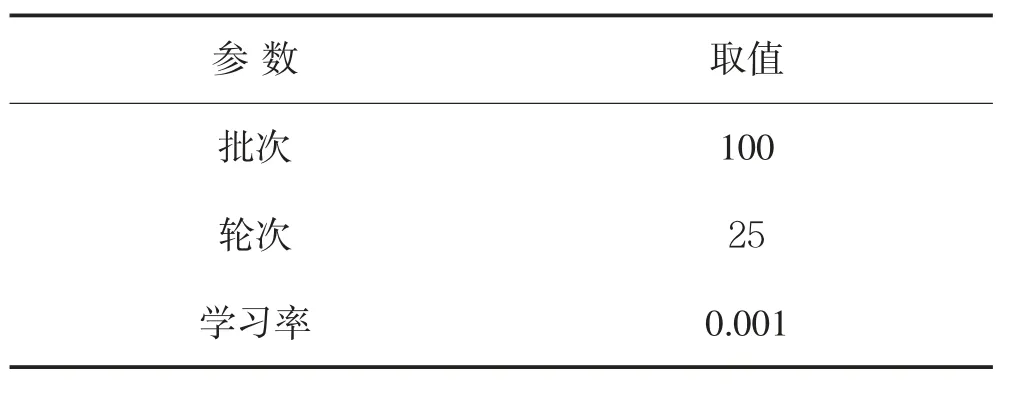
表1 网络参数Table 1 Network parameters

然后,分析检测统计量及检测门限.假设广义协方差矩阵通过训练好的网络后输出特征向量为.根据文献[18],通过引入选择向量ei来选取pk中的值来设置统计量.ei可以表示为

考虑到prk为归一化后的概率,选取prk作为统计量的参考数据.

因此,检测统计量可表示为

其中,φ=Pf.

设置如下频谱感知的规则,即

若Tx≥η 时,则判定主用户信号存在,即频谱被占用,如Tx＜η 时,则主用户信号不存在,即频谱空闲.

3 仿真结果及分析

仿真中CPU 采用Intel（R）Core（TM）i3-10100 CPU.主用户信号为MIMO 信号,其基带调制方式为BPSK,噪声为高斯白噪声,非高斯脉冲干扰通过SαS稳定分布产生.训练样本信号的信噪比范围设置为-19 dB～0 dB,每种信噪比下产生1 000 对数据,并计算得到归一化的广义协方差矩阵作为网络的输入数据.另外生成纯噪声和干扰数据,数据处理方法同上,最终总共产生样本数量为40 000 的测试和训练数据集.网络模型训练的损失函数采用交叉熵函数.训练使用自适应距估计优化算法,学习率设置为0.001.在训练过程中加入了剔除部分参数的Dropout 层,以防网络训练出现过拟合.

为验证基于Transformer 模型的频谱感知方法的有效性,图4 给出了不同信噪比下的ROC 曲线.设置非高斯干扰参数α=1.8,信干比SIR=16.由图4 可以看出,随着信噪比增大,所提方法的检测性能逐渐提升.当信噪比SNR=-14 dB,且虚警概率Pf=0.1 时,所提方法的正确检测概率接近0.8.由此可以说明,在非高斯干扰下所提方法可以有效实现频谱感知.

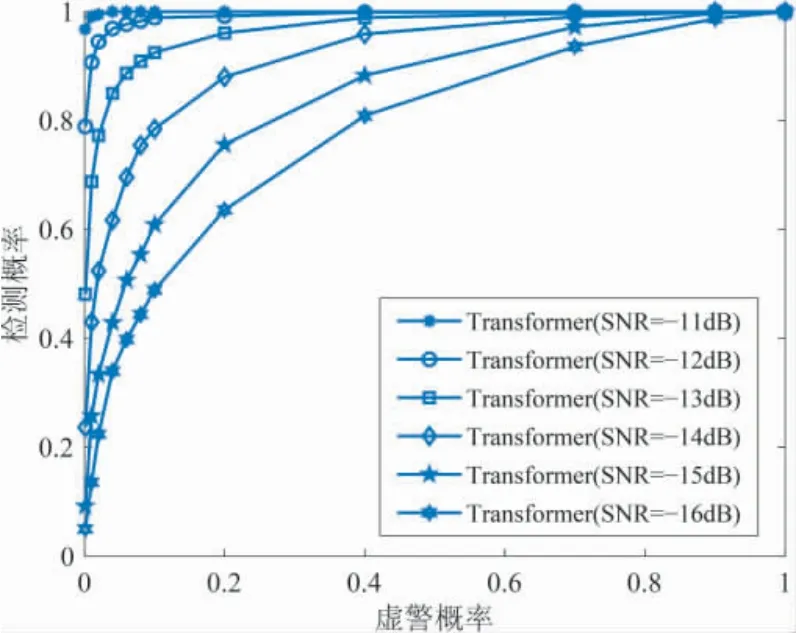
图4 不同信噪比下频谱感知性能Fig.4 Spectrum sensing performance for different signal-to-noise ratios

分析干扰特征指数对算法性能的影响.图5 为不同特征指数α 下的正确检测概率曲线.实验中设置信干比SIR=16,信噪比SNR=-13 dB.可以看出,随着特征指数α 的减小,所提方法的检测概率逐渐下降.由于α 越小,非高斯干扰脉冲特性越明显,即尖峰脉冲值越大,从而导致广义协方差无法表征信号统计特性.此外,如图可知,所提方法在特征指数α≥1.5 的非高斯干扰环境下,可以获得良好的检测性能.

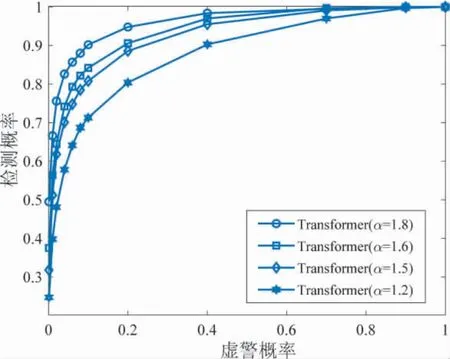
图5 不同干扰特征指数下频谱感知性能Fig.5 Spectrum sensing performance for different interference characteristic exponents

为了分析信干比对检测概率的影响,将信干比分别设置为SIR=0、SIR=5、SIR=10、SIR=16,测试所提方法检测性能,其结果如图6 所示.可以看出,随着信干比的增加,所提方法的正确检测概率总体呈上升趋势.若信干比越大,则接收信号受到非高斯干扰的影响越小,进而信号的统计特性更显著,从而使得检测统计量与检测门限的区分更加明显.

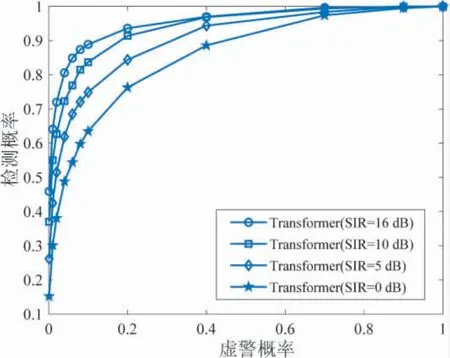
图6 不同信干比下频谱感知性能Fig.6 Spectrum sensing performance for different signal-tointerference ratio

图7 将所提的基于Transformer 模型的频谱感知方法与基于CNN 网络的频谱感知方法进行对比.实验中信号参数保持一致.由图7 可见,在低信噪比条件下,所提方法的性能优于基于CNN 网络的频谱感知方法,但在高信噪比下,两种方法检测性能几乎一致.由此可见,所提方法在低信噪比下具有较强的性能优势.

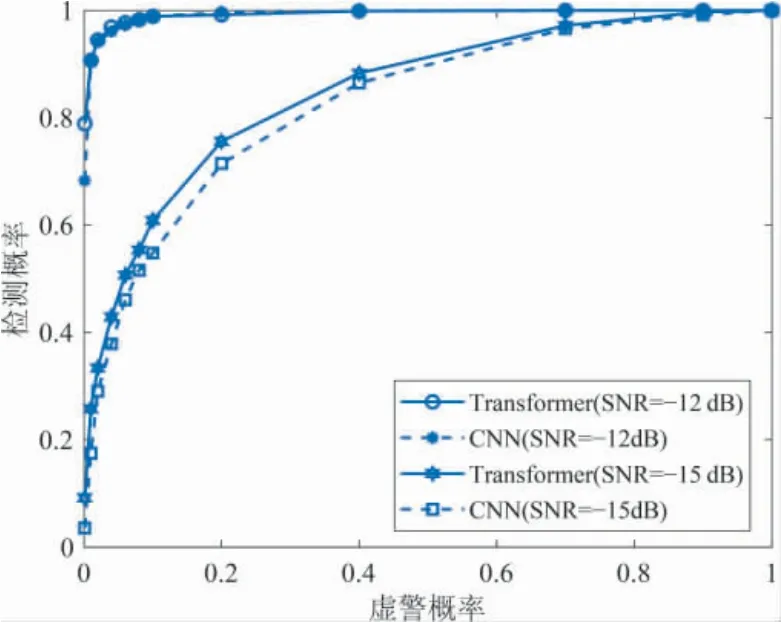
图7 不同网络下频谱感知性能对比Fig.7 Comparison of the spectrum sensing performances in different network

4 结论

研究了高斯噪声与非高斯脉冲干扰环境下多天线频谱智能感知问题,利用Transformer 模型提出一种基于自注意力机制的智能频谱感知方法.该方法分析接收信号的广义协方差矩阵,并将其作为网络输入数据,利用Transformer 模型构建了基于自注意力机制的特征提取网络,在此基础上,利用网络输出特征向量构建二元假设检验方法进行了智能频谱感知.仿真结果表明,所提的频谱感知方法可以有效应对非高斯脉冲干扰下多天线频谱感知问题,且对于脉冲干扰特征指数具有一定的鲁棒性.