基于改进人工势场算法的无人船路径规划

叶军林 何建林 陈孟祥

摘要：针对无人船路径规划中传统势场算法存在的问题，如容易进入局部极小点、航行路径不平滑、在复杂航行环境中目标不可达等，提出了一种改进的人工势场方法。通过增加距离影响因子和改进斥力场函数，解决了上述问题；在无人船行进过程中，通过动态调整斥力参数，并增加逃逸力，使目标点成为全局势场中的最小点；通过在Matlab平台上进行仿真实验，验证了改进后的人工势场方法的有效性。实验结果表明，改进的方法能够克服目标不可达问题和局部极小值问题，同时在计算量和路径规划步数方面具有一定的优势。

关键词：路径规划；人工势场；局部极小值；斥力函数

中图分类号： TP391. 9         文献标识码：A

文章编号：1009-3044（2023）35-0010-06

开放科学（资源服务）标识码（OSID）

0 引言

無人式水面航行器也称水面无人船/艇（Unmanned Surface Vehicle，USV） ，问世已有 70余年的历史，但相比于无人机/车系统，无人船/艇是一种较为陌生的无人化、智能化作业平台。无人船一般用于代替人员执行各种水域复杂任务，其中路径规划技术在无人船舶自主导航中具有极其重要的应用价值。作为核心技术，路径规划旨在解决无人船在存在固定或移动障碍物的环境中如何安全航行的问题。其主要任务是搜索出一条从起点到目标点的路径，该路径既要保证安全无碰撞，又要达到最优或接近最优的效果。

当前，路径规划技术已经相当成熟，并且广泛应用。其中，一些常见的规划方法包括Dijkstra算法、A*算法、人工势场法、模糊算法、粒子群算法、遗传算法、非线性模型预测算法，以及这些算法的改进和融合。Dijkstra算法的优点在于较高的最短路径搜索成功率，然而，该算法的缺点也显而易见。由于需要遍历所有顶点，算法效率较低。A*算法的优点是算法较为简单，易于实现，并且扩展节点数量较少。它能够保证全局最优解的收敛性，然而该算法的缺点是启发函数h（n）的选择不容易。如果启发函数h（n）涉及的信息越多，计算量就会增加，从而导致算法效率降低；相反，如果启发函数提供的信息较少，则算法的准确性可能较差。模糊控制法是一种利用人类已有的驾驶经验结合模糊的环境信息的方法，通过查询表格来确定实时的路径规划策略。然而，这种方法在避障方面的准确度较低。粒子群算法具有随机搜索算法的特点，然而对于高维度的复杂问题，粒子群算法可能会出现早熟收敛现象，导致收敛性能较差，并且无法保证达到最优解。

相较于其他算法，人工势场法在实际无人船路径规划问题中具有较快的反应速度、较高的实时性和较少的计算量，因此在实践中得到广泛应用。然而，在复杂的航行环境中，无人船可能会出现目标不可达和局部最小点问题，导致行进路线规划失效[1]。

针对人工势场法的缺点，国内外学者提出了多种解决方案。其中包括在使用原势场模型的同时消除或逃离局部极小点，构建新的势场函数，以及与智能优化算法相结合[2]。在本文中，采用指数函数构建了一个新的势场函数模型，并根据无人船与障碍物距离的实时调整势场函数的参数，判定无人船陷入局部极小点时增加逃逸力。通过这种方法，解决了传统人工势场法中目标不可达和局部最小点问题，实现了对无人船路径的实时规划。

1 传统人工势场算法在海域环境中的应用

1.1 目标任务

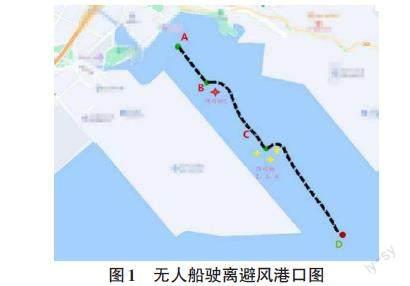
图1为南方某港口，港口内有工作繁忙的船只以及障碍物。现有一艘无人船需要穿过众多障碍物行进到出海口D点完成采集信息任务，采用传统人工势场算法实现该艘无人船从起始点A到目标终点D的路径规划，航迹如图中黑色虚线所示。

1.2 传统人工势场算法做路径规划

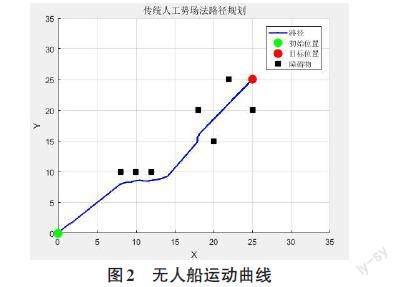
人工势场法是通过模拟粒子在势场中的运动，将无人船的路径规划问题转化为在势场中的运动问题。在人工势场法中，通常将目标点视为吸引子（attraction） ，将障碍物视为斥力（repulsion） 。无人船会受到目标点的吸引力和障碍物的斥力影响，从而生成一条避开障碍物、朝向目标点的路径。人工势场法包括吸引子势场和斥力势场两个基本组成部分。吸引子势场（Attraction Field） ：吸引子势场用来引导无人船朝向目标点，通常采用逆距离的方式定义吸引子势场，即目标点越近，吸引力越强；这样，无人船会受到目标点的吸引力，朝着目标点移动。斥力势场（Repulsion Field） ：斥力势场用来避开障碍物，障碍物被视为斥力源，斥力的大小和距离成反比；当机器人接近障碍物时，斥力增大，使无人船受到斥力的作用而避开障碍物。通过在空间中叠加吸引子势场和斥力势场，无人船会受到吸引力和斥力的综合影响，从而产生一个合适的移动方向。无人船根据当前位置和势场的梯度信息，选择一个最优的方向进行移动，实现路径规划，如图2所示。

1.3 传统人工势场算法模型

无人船能从港口起始点A航行到目标终点D，是因为无人船航行过程中受到吸引子势场的作用，吸引子势场为矢量，大小取决于无人船当前位置与目标终点的距离，方向由无人船指向目标终点。吸引子势场的表达式如式（1） 所描述。

[Uatt=12kx-xg2+y-yg2] （1）

式中为k为吸引子势场参数，（x，y） 和（[xg，yg]）分别是为无人船运动当前时刻在坐标轴位置和目标终点位置。

吸引力定义为吸引子势场的负梯度[3]，如式（2） 所示。

[Fatt=-∇Uatt= -kx-xg，-ky-yg] （2）

吸引力的大小为：

[|Fatt|=k x-xg2+y-yg2] （3）

由式（3） 知无人船离目标点距离愈远，引力越大，反之亦然。

无人船在起始位置A点受到的斥力势场由表达式（4） 所描述。

[Urep=12m1ρ-1ρo  ，ρ<ρo0                         ，ρ≥ρo ] （4）

式中，m为斥力势场系数，[ρ]为无人船当前位置与障碍物之间的距离，[ρo]为障碍物对无人船的斥力势场影响距离。求取排斥力势场函数[Urep]的负梯度即可得到排斥力表达式（5） 。

[Frep=-∇Urep= mρ2 1ρ-1ρo[∂Urep∂x，∂Urep∂y]] （5）

障碍物对无人船的斥力大小函数为：

[|Frep|=mρ2 1ρ-1ρo  ，ρ<ρo0                       ，ρ≥ρo] （6）

根據公式（6） 的观察，当无人船靠近障碍物时，它受到的斥力与无人船与障碍物之间的距离成反比。为了更清晰地表示无人船受到的排斥力，将其分解到xy坐标系上。排斥力与坐标轴的夹角可以通过式（7） 计算。

[θ=cos-1（x-xdx-xo2+y-yo2）] （7）

排斥力在xy坐标轴的分量为：

[|Frep-x|=|Frep|cosθ  ，ρ<ρo0                         ，ρ≥ρo]

[|Frep-y|=|Frep|sinθ  ，ρ<ρo0                         ，ρ≥ρo] （8）

无人船在航行过程中收到的总势场为U=[Urep]+[Uatt]，总合力为F=[Fatt]+[Frep]。

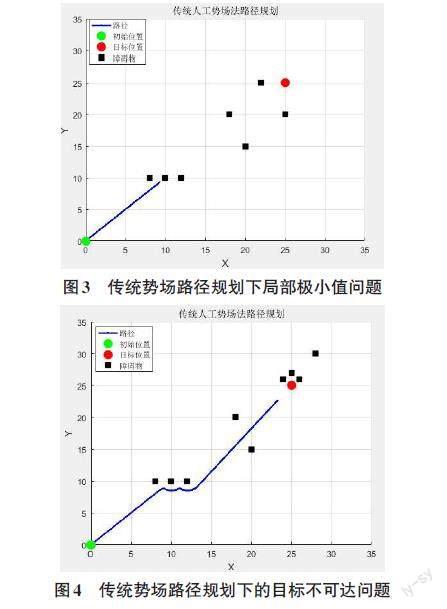
1.4 经典人工势场法路径规划问题

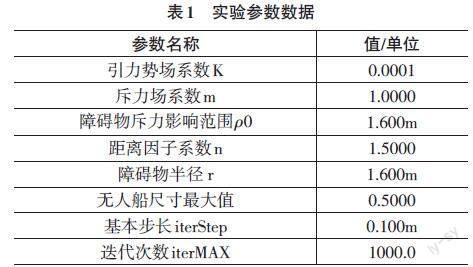
结合1.1节的目标任务可知：在理想情况下，无人船受到目标点的吸引子势场和障碍物的斥力势场的联合作用，会自动识别路径中的障碍物并避开，不断接近目标点，实现整个航行。然而，有时在特定情况下，出现了局部极小点的情况，导致无人船在某个位置停止而无法继续沿规划路径前进。在图3路径规划仿真中，当无人船经过航迹点B时，起始位置A、障碍物位置B和目标终点位置D位于同一直线上，此时，目标终点D对无人船的吸引力和障碍物B对无人船的斥力叠加后为零，这将导致无人船的运动陷入局部极小值。这种情况是人工势场法的一个局限性，称为局部最小点问题。图4是在传统人工势场路径规划下遇见的无人船在目标处震荡的问题。

2 改进人工势场算法

针对无人船路径规划中的目标不可达和限于目标极小点问题，可以考虑以下解决方法。动态调整势场参数：通过动态调整势场函数的参数，可以改变吸引力和斥力的权重，从而优化路径规划结果；可以根据实际情况，根据障碍物的距离、目标点的位置等因素，自适应地调整参数，以提高路径可达性。引入逃逸力机制：在势场法中引入逃逸力，可以帮助无人船从局部最小点中脱离出来；逃逸力可以根据当前位置和势场梯度的信息，提供一个额外的推力，使无人船能够跳出局部最小点并重新搜索更优路径。逃逸力的大小和方向可以根据具体需要进行调整。

2.1 解决目标点不可达问题

大多数学者对人工势场的改进主要集中在斥力势场函数上，其中使用的函数通常是基于无人船与障碍物相对位置的倒数的二次函数。然而，这种函数在实际应用中存在一些问题，因为即使无人船做出轻微的移动，势场的强度会发生剧烈变化，这对路径判断造成了困扰。鉴于此，本文选择使用指数函数来改进斥力势场函数，以减缓斥力场强度的变化速度。

同时，为了解决目标不可达的问题，引入了目标点与无人船相对位置的考虑。通过将改进的斥力势场函数乘以一个因子，使得目标点位置的斥力为零，可以确保无人船朝着目标点的方向移动而不受斥力的干扰。改进后的斥力势场函数如式（9） 所示[4，9]。

[Urep=12m1ρ-1ρo2 [1-exp（-x-xg2+y-yg2r2）] ，ρ<ρo0，ρ≥ρo] （9）

对式（9）的斥力势场函数求负梯度即可分解为两个方向的排斥力[Frep-x]和[Frep-y]，[Frep-x]的方向由障碍物指向无人船，[Frep-y]的方向由无人船指向目标，大小如式（10） 所示。

[[Frep-x=-∇xUrep= -m 1ρ-1ρo2x-xgexp（-x-xg2+y-yg2r2]  ]

[+m [1-exp（-x-xg2+y-yg2r2）1ρ-1ρox-xoρ3]]

[Frep-y=-∇yUrep= -m 1ρ-1ρo2y-ygexp（-x-xg2+y-yg2r2]]

[+m [1-exp（-x-xg2+y-yg2r2）1ρ-1ρoy-yoρ3]]] （10）

由式（10） 可知：当无人船接近目标点，[x-xg2+y-yg2→0]，可推导出斥力的合力大小[|Frep|→0]。

在这个改进的斥力势场函数中，当无人船靠近目标点附近的障碍物时，无人船受到的排斥力为零。这意味着无人船不再受到障碍物的排斥力的影响，并且只受到目标点的引力作用，使得无人船能够在目标点附近自由移动，解决了传统人工势场算法中的目标点不可达问题。

2.2 解决局部极小点问题

为了使得无人船能顺利到达目标点或者使陷入局部极小值的无人船能逃脱局部极小值点到达目标点，根据无人船与障碍物距离的远近动态调整斥力函数参数、增加逃逸力。结合无人船与障碍物距离调整势场力参数，增加逃逸力，使陷入局部极小值点的无人船摆脱陷阱，抵达目标点。

首先判断无人船是否进入极小值点，无人船移动的连续5个步长可以用作判断无人船是否陷入局部最小点的依据[5]。如果在这5个连续步长小于[α] *iterStep，[α∈][ 2，4] 时，通过调节[α]值，可较快地检测无人船是否陷入局部最小。根据无人船与障碍物的距离，调整斥力函数的参数[ρo]和r；当判断出无人船已经陷入局部最小时，按式（11） 设计逃逸力。

[Frepx（i）=σ*Frep-x（i）*cos（angle_re（i））Frepy（i）=γ*Frep-x（i）*sin（angle_re（i））] （11）

式中：[σ]，[γ]为逃逸力系数，[Frep-x（i）]为当前障碍物指向无人船的斥力函数分量，[angle_re（i）]为障碍物指向无人船向量与X轴之间的夹角，[Frepx（i）]和[Frepy（i）]为逃逸力在坐标轴上的分量。无人船跳出局部极小值之后，撤回逃逸力，无人船在原势场作用下继续路径规划算法[6，10]。

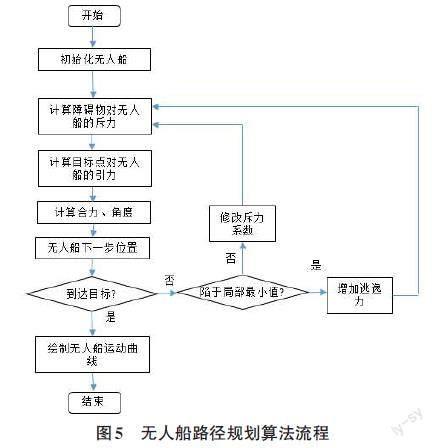
2.3 算法流程

无人船路径规划的算法流程如图5所示。首先，在无人船路径规划的开始阶段，需要对无人船的起始点、目标点和障碍物的位置进行初始化，确定它们在坐标系中的位置。其次，在无人船航行的过程中，需要持续计算障碍物对无人船的斥力和目标点对无人船的吸引力。再次，对合力进行计算，由引力、斥力和合力值计算当前无人船的角度，根据步长和当前位置计算下一迭代位置；再次，判断无人船是否陷入局部最小值状态。如果无人船无法继续航行或无法显著改变其位置，那么可以推断它可能陷入了局部最小值点，通过调整斥力参数和引入逃逸力，帮助无人船摆脱局部最小值点。如果不是陷入局部最小值，调整参数，驶离复杂障碍物环境；最后绘制无人船从起点到目标点的完整规划路径[7]。

3 仿真实验

实验假设无人船的航行范围是一个大小为35m×35m的区域，人们在该区域内随机布置了多个障碍物，并测得它们的位置坐标。下面是每个障碍物的位置坐标：障碍物1（5，5） ，障碍物2（16，18） ，障碍物3（17，19） ，障碍物4（19，20） ，障碍物5（20，20） ，障碍物6（20，19） ，障碍物7（21，18） ，设无人船的初始位置X 为（0，0） ，目标点的位置Xg为（25，25） 。仿真系统基本参数设计，见表1，用Matlab R2016a进行仿真。

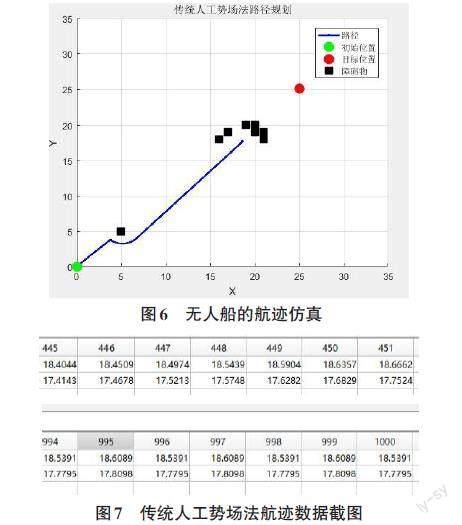
在简单的障碍物环境中，如图6所示，当障碍物位置与目标终点临近时，采用传统人工势场算法进行无人船航迹仿真，发现无人船无法到达目标；在Matlab仿真中截取了无人船的部分航迹数据，如图7所示，发现无人船抵达（ 18.6，17.6） 坐标位置后，即使再行进551次，依然停留在原地，从而判断无人船已经陷入了局部最小值。

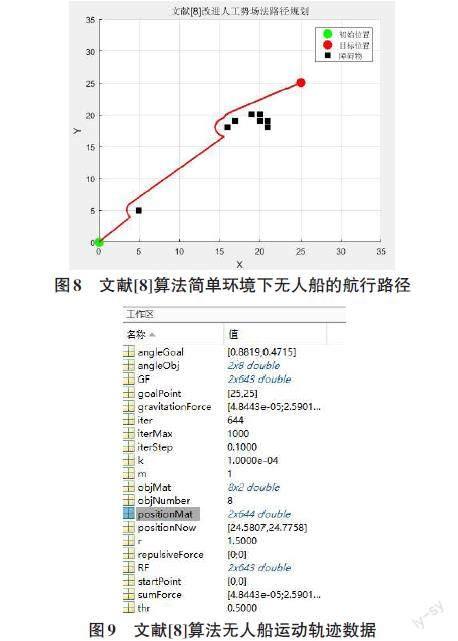
利用引用为[8]的文献中所提出的算法[8]，在一個简单的障碍物环境中进行了仿真实验。根据仿真结果，无人船的航行轨迹如图8所示，在这个路径中，无人船沿着障碍物的边缘移动，并成功跳出了局部最小值点。图9展示了仿真实验的Mablab工作窗口数据，从中可以看出该算法经过了644次迭代才到达目标点。

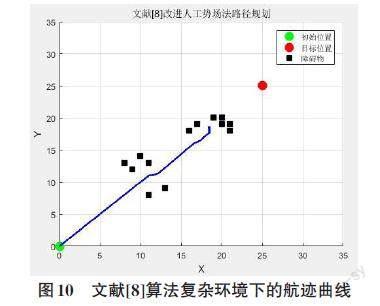
进一步提升无人船的航行环境复杂度，增加了障碍物的数量，并更改了它们的坐标位置。下面是新的障碍物位置坐标：（8，13） ，（9，12） ，（10，14） ，（11，13） ，（11，8） ，（13，9） ，（16，18） ，（17，19） （19，20） ，（20，20） ，（20，19） ，（21，19） ，（21，18） 。根据引用为[8]的文献中所提出的算法，在仿真实验中得到了无人船的运动轨迹曲线，如图10所示。从该图所示的航行轨迹曲线可以看出，无人船到达凹形区域时，陷入了局部最小值点的困境[11-13]]。

根据本文所提出的改进人工势场算法，进行了仿真实验。在无人船向目标点航行的过程中，可以通过判断无人船与障碍物之间的距离来实现障碍物的避障。当无人船进入障碍物的影响距离时，可以根据与障碍物的实时距离选择不同的斥力系数，调整无人船受到的斥力大小，避免无人船陷入局部极值点；无人船在复杂航行环境中时，如在凹型障碍物中陷入局部极值点，通过调整斥力势场系数和增加逃逸力，使无人船逃离凹型障碍物脱离局部极值点[14]。

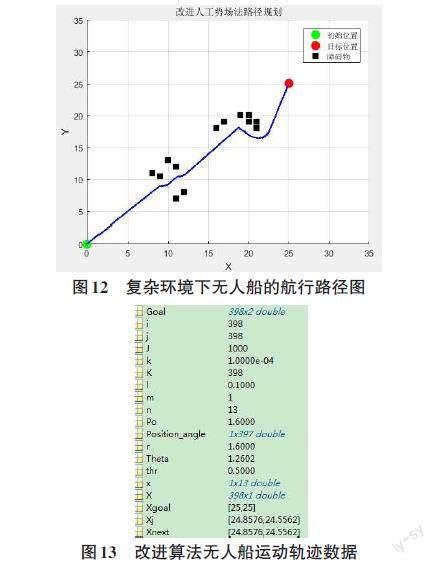
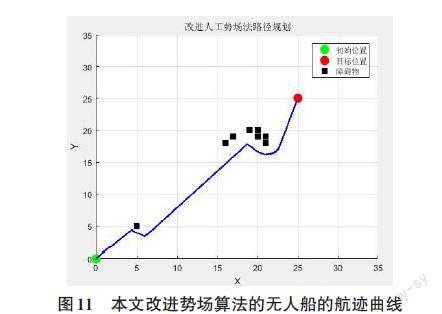
参照表1中仿真系统的基本参数，当限于局部极值点且无人船与障碍物的距离小于[ρ0]/2时，逃逸力系数σ=1.1，γ=-0.9，调整斥力函数系数r=1.8，[ ρ0]=1.8。根据本文提出改进算法，分别绘制无人船在简单航行环境中和复杂航行环境中的运行轨迹如图11和12所示。图13是复杂航行环境中无人船的移动步数，经过398 步无人船到达目标点。

仿真图6至图13，是在相同环境下，采用3种不同算法模拟无人船的路径规划。传统人工势场算法在本文提供的简单障碍物环境中陷入局部最小值；文献[8]改进算法引入距离因子，在简单障碍物环境中经过644步无人船可以抵达目标，但在复杂障碍物环境中陷入局部最小值；采用本文提出的算法，无人船在两种障碍物环境中均能抵达目标，且移动的步数相比文献[8]改进算法的步数大大降低。

4 结束语

针对传统人工势场算法在路径规划应用中常见的问题，本文提出了一种改进算法，采用指数函数改进斥力函数，并引入无人船与障碍物之间的距离因子改善目标不可达的问题；同时，当无人船陷入局部最小值时，根据无人船与障碍物之间的距离动态调整势场模型系数，并增加逃逸力以帮助无人船快速跳出局部最小值点，是一种有效的改进方法。通过这种方法，可以使无人船在面对简单或复杂的障碍物环境时，具备躲避障碍物、逃离局部最小值点并平滑到达目标点的能力。航行步数比参考文献[8]更加优化，满足了无人船实时路径规划的要求[15]。

参考文献：

[1] 薛飞.基于无人船的路径规划与避障问题研究[D].哈尔滨：哈尔滨工程大学，2017.

[2] 刘传领.基于势场法和遗传算法的机器人路径规划技术研究[D].南京：南京理工大学，2012.

[3] 刘琨.基于人工势场和蚁群算法的无人船路径规划研究[D].海口：海南大学，2016.

[4] 栾天宇.无人船自动驾驶系统的设计与实现[D].北京：北京理工大学，2018.

[5] 刘瀛.基于改进势场与蚁群算法的机器人路径规划法[J].计算机仿真，2021，38（11）：355-360.

[6] 张佳尚，陈志华.基于预添加虚拟力的改进人工势场算法[J].兵器装备工程学报，2023，44（3）：219-225.

[7] 罗强，王海宝，崔小劲，等.改进人工势场法自主移动机器人路径规划[J].控制工程，2019，26（6）：1091-1098.

[8] CHEN Y Q，LI T X.Collision avoidance of unmanned ships based on artificial potential field[C]//2017 Chinese Automation Congress （CAC）.Jinan，China.IEEE，2017：4437-4440.

[9] YU J B，DENG W，ZHAO Z Y，et al.A hybrid path planning method for an unmanned cruise ship in water quality sampling[J].IEEE Access，2019，7：87127-87140.

[10] LYU H G，YIN Y.Ship’s trajectory planning for collision avoidance at sea based on modified artificial potential field[C]//2017 2nd International Conference on Robotics and Automation Engineering （ICRAE）.Shanghai，China.IEEE，2017：351-357.

[11] 許万，程兆，朱力，等.一种基于改进人工势场法的局部路径规划算法[J].电子测量技术，2022，45（19）：83-88.

[12] 江明，王飞，葛愿，等.基于改进蚁群算法的移动机器人路径规划研究[J].仪器仪表学报，2019，40（2）：113-121.

[13] 陈继清，谭成志，莫荣现，等.基于人工势场的A*算法的移动机器人路径规划[J].计算机科学，2021，48（11）：327-333.

[14] 刘涛，贾立校，曹翔.动态人工势场法的无人船避障路径规划[J].舰船科学技术，2023，45（5）：89-92.

[15] 余必秀，初秀民，柳晨光，等.基于改进A*算法的无人航道测量船路径规划方法[J].武汉大学学报（信息科学版），2019，44（8）：1258-1264.

【通联编辑：梁书】