基于六关节机械臂的推拿按摩康复机器人运动学研究*
2024-01-25高红卫魏宏波鲁开讲
高红卫,魏宏波,鲁开讲
(宝鸡文理学院 机械工程学院,陕西 宝鸡 721016)
六关节机器人是目前普通高校和企业广泛用于实验教学和自动化作业的一种典型自动化设备。如图1所示,六关节机器人具有结构简单、运动灵活、通用性强等优点,常被应用于搬运、装配、焊接等众多应用领域,它的工作空间和奇异位形对工作性能有重要影响,因此,研究该类机器人具有很重要的实际意义。在机器人的设计中,工作空间及奇异位形是非常重要的技术指标。工作空间是机械手参考点能够到达的空间区域,它决定了机器人的作业范围;奇异位形是机构的固有性质,也是机器人机构的一个十分重要的运动学特性。机器人的运动、受力、控制以及精度等诸方面的性能都与机构的奇异位形密切相关。深入研究机器人的奇异位形进行,以避开奇异位形并且减少和消除奇异位形的影响,有助于对该类工业机器人的设计及优化。近年来,关节机器人已成为机器人研究的一个重要方面。许卫斌等[1]提出了一种将MATLAB中Sim-Mechanics模型与蒙特卡洛法相结合的机器人工作空间求解方法。田海波等[2]提出了自适应划分网格方法并用于计算工作空间的体积。侯雨雷等[3]提出了“极限定步距角法”,并用于提取工作空间边界。徐有胜[4]运用Solidworks建立机器人三维模型,并在MATLAB中进行动力学仿真,对动力学算法进行优化。
近年来,传感技术、智能控制技术及其它新兴技术的迅速发展促进了医用机器人的发展。人们尝试利用智能化的按摩机器人来代替按摩专家。2006年日本丰桥大学[5]研发出具有仿人手的多关节按摩机器人,实现了对各个手指按摩力度的控制。ALAVANDARS et al[6]设计了具有5自由度机械臂的按摩机器人,采用图像测量技术和遗传算法分析了腿部肌肉按摩运动的轨迹。PENG et al[7]设计了5自由度机械臂和4手指仿人手,可完成按、揉、拿3种手法。陈俊等[8]基于中医推拿手法设计了一款仿生按摩装置末端执行器及按摩机器人,采用线性度评估了推拿机器人对医生手法推拿力度和按摩行程的重现度。高焕兵等[9]研制出了具有单机械臂的第二代中医按摩机器人产品化样机的几何模型和三维装配模型。张营等[10]基于遗传算法优化和BP神经网络实现按摩机器人对患者做出精确的治疗方案行为决策。杜光月等[11]将神经网络理论用于设计按摩机器人人体穴位定位,实现按摩机器人自动寻找穴位的功能。张明亮等[12]针对推、按、揉、滚4种推拿手法的运动特征,给出并联机构执行器的拓扑结构和三维模型。曾达幸等[13]通过分析几种典型中医推拿手法特征所需的自由度配置,提出一种适合中医推拿手法运动特征的5自由度解耦串并联中医推拿机器人机构。
对于中小零售企业电子商务商业运营模式运行管理体系而言,顾客界面是较为关键的组成元素,主要涉及目标客户、管理渠道以及服务与品牌建设等,从而维护相应产品信息和服务对象,一定程度上在网络中树立关键的企业品牌形象,为后续服务管理工作的全面开展奠定基础。
长白猪的妊娠期第三胎与第一胎比较差异有统计学意义(P<0.01),第二胎与第一胎比较差异有统计学意义(P<0.05);大白猪的妊娠期第一胎和第二胎、第三胎之间比较差异均无统计学意义(P>0.05),但第三胎有显著高于第二胎的趋势(P=0.07);长大二元猪的妊娠期第三胎和第二胎与第一胎间比较差异具有统计学意义(P<0.01)。见表1。
本文针对目前康复推拿设备普遍存在手法单一,无法实现适宜于不同对象个性化手法方案的缺陷,将RBT-6T/S03S型关节机器人用于推拿按摩机器人的执行机构,设计了推拿机器人总体方案和多关节、多指推拿按摩机械手,为了精确实现影响推拿按摩治疗效果的位移、速度冲量、加速度惯量等刺激量,对机器人本体及推拿按摩机械手运动学进行了必要的研究。
1 康复推拿机器人总体方案设计
中医专家在推拿理疗中的手法可划分为2类,第一类仅由指关节实现,其运动特征可用手指上的特征点的轨迹来描述,这类动作可由2~3个手指的协调动作来完成,为实现这类手法需设计多关节多指机械手。第二类由腕关节和肘关节的转动来实现,此时不考虑指关节运动,将手部运动描述成绕某轴的瞬时转动,这类手法由机器人手腕的三维转动来实现。
根据表1感官评分结果,工艺B>工艺A>工艺C,即蓝莓打浆添加果胶酶0.1 g/kg,添加白糖150 g/kg并添加酵母0.2 g/kg,经低温预发酵72 h后25℃主发酵30 d,过滤离心后添加偏重亚硫酸钾和果胶酶各0.2 g/kg,然后杀菌灌装成品酒。
为了用数值法搜索机器人工作空间,需要从式(1)(2)(3)求出关节转角,式(1)(2)(3)是以3个关节转角为未知量的三角超越方程组。
2 机器人机构运动学参数描述
求得θ2后,将式(3)整理成

图2 康复推拿机器人系统Fig. 2 Rehabilitation massage robot system

表1 连杆运动学参数(D-H参数)Tab. 1 Analysis of athletics parameters for connecting rod (D-H parameters)
3 机器人位置工作空间分析
RBT-6T/S03S型工业机器人后面3个关节Ⅳ、Ⅴ、Ⅵ轴线交于一点O4,只是用来改变末端机械手的姿态,故机器人能到达的空间区域主要取决于前3个关节,关节Ⅳ、Ⅴ、Ⅵ轴线的交点可作为机械手参考点,其运动范围可用来描述机器人的工作空间。参考点O4在机器人基座坐标系的位置矢量为:
r=d1k1+a1i1+…+a3i3+d4k4
(1)
其中,di,ai分别表示连杆运动学参数;km(m=1,2,3,4),in(n=1,2,3)分别为机器人连杆坐标系的x,z轴方向的单位矢量。
模型中,i和t分别表示不同省份和年份;C1、C2、C4分别表示投资、技术创新和人口对产业结构升级的作用效应;C3表示非老龄人口比例对产业结构升级的影响,当C3>0时,表示老龄化程度越高,越不利于产业结构升级;C5表示分配给劳动人口的资源比例对产业结构升级的影响,当C5<0时,表示分配给老龄人口的资源越多,越能促进产业结构升级。
研究区岩性主要为沉积岩.1928年,我国著名地质学家杨曾威、李春昱和黄汲清等在此作了很多工作,并研究了杨家坨煤系的沉积特征,对本地区杨家坨煤系地层进行了划分;1963年,杨士恭对下杨家坨煤系上部地层,首次使用了灰峪组之名,1976年北京矿务局也将其命名为灰峪组,使该地层成为石炭系上统北京地区代表剖面[5].同年(1976年),北京矿务局分别在本地区的岔儿沟东侧及岔儿沟与阴山沟分水岭上测得二叠系下统地层代表剖面,并分别命名为岔儿沟组和阴山沟组[5].至此,以军庄镇地名命名的石炭系上统和二叠系下统的地层剖面,成为北京地区上古生界地层的代表剖面.
坐标形式为:
x=cθ1[(a3c(θ2+θ3)-
d4s(θ2+θ3)+a2cθ2+a1)]
(2)
y=sθ1[(a3c(θ2+θ3)-
d4s(θ2+θ3)+a2cθ2+a1)]
(3)
z=-a3s(θ2+θ3)-d4c(θ2+θ3)-a2sθ2
(4)
由于初等变换是以Jii≠0(i=1,2,…,5)为前提的,所以机器人发生奇异的判别条件为:
康复推拿机器人系统总体方案如图2所示。在人体推拿部位建立人体坐标系{Q},通过双目视觉定位原理标识推拿的特定部位规划手指特征点的运动轨迹和机械手姿态变化轨迹,经过环境坐标系{P}将运动轨迹变换到参考坐标系{U}。另一方面上述轨迹也可由推拿机械手或工具坐标系{T}经机器人末端坐标系{H}和基坐标系{B}变化到参考坐标系{U},由此建立人体坐标系到机械手坐标系变换方程,得到推拿过程中机械手姿态和手指特征点运动规律。
利用(2)×sθ1-(3)×cθ1可以同时消去θ2和θ3,得到仅含一个未知数θ1的方程(5)。
-xsθ1+ycθ1=0
(5)
可求得:
(6)
作运算(2)×cθ1+(3)×sθ1,并与式(4)联立,移项得:
xcθ1+ysθ1-a2cθ2=
a3c(θ2+θ3)-d4s(θ2+θ3)
(7)
z+a2sθ2=-a3s(θ2+θ3)-d4c(θ2+θ3)
(8)
由式(7)(8)平方和可以消去右边c(θ2+θ3)和s(θ2+θ3),得到关于未知数θ2的方程。
Asinθ2+Bcosθ2+C=0
对上式的系数化简得:
RBT-6T/S03S型工业机器人是由6个转动关节串联的开式运动链,相邻构件之间的相对运动可以用运动螺旋来表示。末端机械手的运动为各关节运动螺旋的线性组合:
机器人运动螺旋系线性相关时,矩阵J的行列式等于零。
(9)
RBT-6T/S03S型工业机器人是由6个转动关节将各连杆连接而成的开式运动链,其结构如图2所示。关节的传动采用模块化结构,连接前3个关节的连杆具有较大的长度,使得机器人具有足够的位置空间,后面3个关节轴线交于一点,只用来改变末端机械手的姿态,可用来实现推拿理疗的第二类手法。运动链的一端装在固定的基座上,另一端处于自由状态,可安装各种工具以实现机器人作业。用D-H方法在每个构件上建立连杆坐标系,确定机器人各连杆的运动学参数,如表1所示。
《四库全书总目·蜀中广记提要》曾评论曹氏此书云:“舛讹牴牾,亦时时间出。盖援据即博,则精粗毕括,同异兼陈,亦事势之所必至,要之不害其大体。”有关此词本事之记载,显属此类。事实上,黄庭坚所言“昨日市中已见腊梅,开者数枝矣”数语是写信给王直方的,也未必作于戎州。
A′sinθ3+B′cosθ3+C′=0
其中,A′=a3cθ2-d4sθ2,B′=a3sθ2+d4cθ2,C′=z+a2sθ2。于是可求得:
(10)
得到关节转角的表示式θi=θi(x,y,z)(i=1,2,3)后,机器人的工作空间的点满足的解析条件为:其坐标使得每个关节转角θi(x,y,z)至少存在一个解满足关节结构约束条件θi(x,y,z)∈[θimin,θimax],在数学上机器人工作空间满足下式条件点的集合:
Ω={∀P(x,y,z)∈Ω|∃θi(x,y,z)∈
[θimin,θimax](i=1,2,3)}
(11)
为了寻找机器人的工作空间,在机器人的工作空间内随意找到一个点D(x0,y0,z0),建立局部坐标系D-x′y′z′,将机器人的位置在局部坐标系中用球坐标式表示,并转化到参考坐标系:
(12)
其中,ρ∈[0,∞),δ∈[0,π],φ∈[0,2π]。
为了搜索机器人的工作空间,在3个参数(ρ,δ,φ)中先固定其中2个(δ,φ),在每个(δ,φ)给出的方向上,让向径ρ从0开始递增,将式(12)代入θ1,θ2,θ3的表达式(6)(9)(10),若得到的θ1,θ2,θ3均至少有一解在关节转角的变化范围,否则,只要有一个关节角超出关节变化范围,继续增大向径ρ直到某个关节转角所有解超出其变化范围,则该点不属于该机器人的工作空间,由此可以得到(δ,φ)给出的方向上的边界。循环δ和φ则可以得到各个方向的边界,从而可以得到机器人的工作空间范围,如图3所示。

图3 机器人的工作空间Fig. 3 The workspace of robots
4 机器人的奇异位形分析
可求得:
其中,ωi,ω分别为各关节相对转动角速度和末端机械手转动角速度;$i表示关节运动螺旋,可由机器人运动参数表示。
螺旋是机器人位形的函数,当6个运动螺旋线性无关时,末端机械手就有6个自由度,可以实现空间六维运动。当机器人处于某些特定位形使得6个运动螺旋线性相关,末端机械手将失去部分自由度,关节运动对末端机械手的运动丧失控制作用,这时即使关节运动,而末端机械手可能不动或只能作少于6个自由度的运动,将这些位形称为机器人奇异位形。为了得到运动螺旋发生线性相关的条件,将机器人运动螺旋系写成矩阵,并通过初等变换化成上三角矩阵:
基于群体药动学原理对1例甲氨蝶呤严重排泄延迟患儿的药学监护 ……………………………………… 李思婵等(4):560
式中,x,y,z分别表示机械手参考点在基座坐标系下的位置坐标;cθi表示cosθi;sθi表示sinθi。
(13)
综合分析以上条件可以得出机器人发生奇异的条件为:
s5=0∪f(θ1,θ2,θ3)=0
s5=0表示当θ5=0或π时关节轴线4和6共线,$4=$6。在J66的表达式中,f(θ1,θ2,θ3)是关于角度θi(i=1,2,3)组合的正余弦函数表达式:
f(θ1,θ2,θ3)=sin(A1θ2+B1θ3+C1)·
sin(A2θ2+B2θ3+C2)·
sin(A3θ2+B3θ3+C3)
(14)
其中,系数Ai,Bi(i=1,2,3)为机器人运动参数的复杂函数。
(2)“I want each of you to know that you were the best campaign anybody could have ever expected or wanted.”(Hillary Clinton,2016)
根据奇异位形的判别条件(14),借助MATLAB软件,搜素奇异位形曲面,得到6自由度串联机器人的奇异位形及其对工作空间的划分,如图4所示。
很多时政热点能体现时代的特点、社会的主流价值观以及国家的重大方针和政策;近几年的思想政治高考试题考查时政热点的趋势比较明显。因此,将时政热点引入课堂教学十分必要。在思想政治教学中加强时政教育可以深化中学的政治理论教学,增强教育教学的生命力和凝聚力;还能够有效弥补教材的滞后性,培养学生理论联系实际分析解决问题的能力,提高学生道德品质;同时,能丰富教学内容,帮助学生深刻理解理论知识,提高政治教学的时效性与有效性。
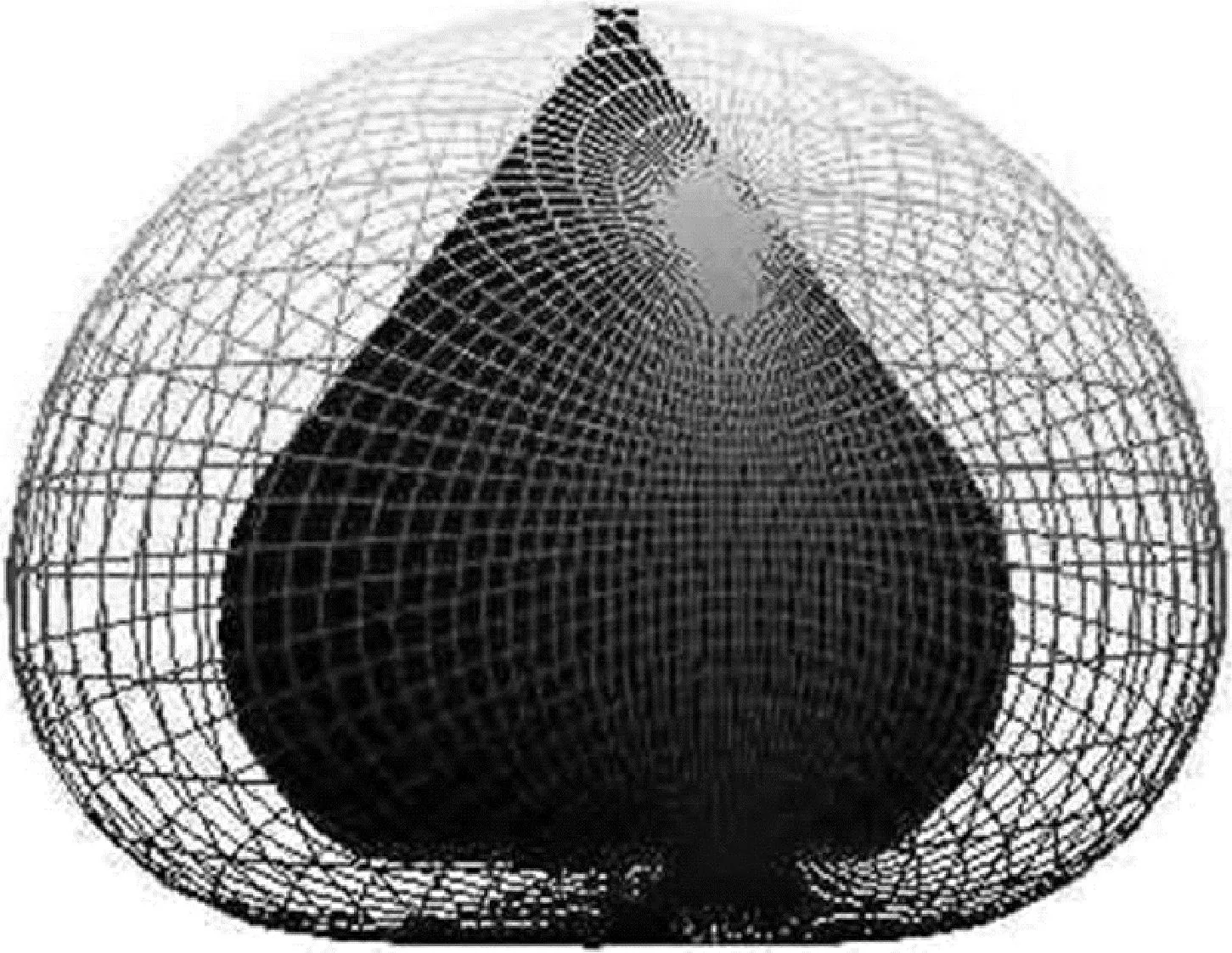
图4 六关节机器人的奇异位型Fig. 4 Singular configuration of a six joint robot
5 多关节多指推拿按摩机械手设计
中医专家在推拿理疗过程中的第一类动作是通过指关节的运动实现的,其运动特征可用手指上的特征点的轨迹来描述,这类动作可由2~5个手指的协调动作来完成。在机器人末端安装多指多关节机械手,如图5所示,再现推拿按摩过程中手指特征点的轨迹。
二是优化居家公共服务。完善社区党群服务中心阵地功能,将社会保障、公共卫生、社会救济、法律援助、卫生保健等16大类52项政府公共服务项目下移到社区,实行“一条龙”服务、“一站式”办理、确保群众小事不出社区就能尽快办结。推行社区干部便民事务代办机制,对不涉及对上协调的即办类事项,由社区干部根据群众申请,现接现办;对涉及对上协调的代办类事项,由社区干部下载、帮代填写相关资料后,指导帮办;对老弱病残等弱势群体、特殊事项,由社区干部根据群众申请,全程陪同办理,开启为民服务“直通车”。

图5 多指多关节机械手Fig .5 Multi-finger and multi-joint robotic arm
基于位置正解,即让每个指关节变量在其结构约束允许的范围内依次取所有值
[θimin]≤θi≤[θimax],i=1,2,…,4
(15)
手指上特征点的坐标能到达的点的集合,就构成手指的工作空间。显然这样获得的工作空间呈点云状,如图6所示。
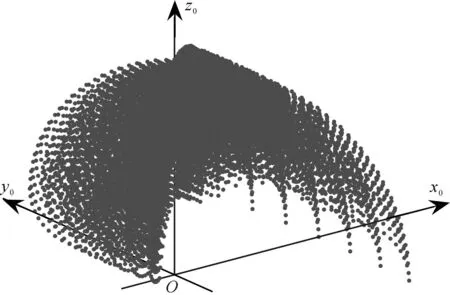
图6 手指的工作空间Fig. 6 Workspace of finger
6 小结
工作空间和奇异位形是衡量并联机构运动学性能的2个重要方面。本文以RBT-6T/S03S工业机器人为对象,根据其结构特点,提出描述机器人位置工作空间的方法。通过机器人位置反解,得出影响机器人工作空间的关节转角表达式,给出了工作空间的数学描述。利用机器人运动螺旋系的线性相关性建立机器人奇异位形的判别准则,得到机器人发生奇异的运动学条件和奇异位形曲面解析方程。并利用MATLAB软件进行分析计算,得到了6自由度机器人的奇异位形,对该类型机器人的设计及实际应用具有指导意义。结合中医手法,研究了机器人手腕和多关节多指的运动学,实现了适宜个性化按摩理疗所需的手法,并为影响按摩效果的运动学和动力学刺激量的控制提供了基础,有较好的应用前景。
