Effects of carrier density and interactions on pairing symmetry in a t2g model
2024-01-25YunXiaoLi李云霄WenHanXi西文翰ZhaoYangDong董召阳ZiJianYao姚子健ShunLiYu于顺利andJianXinLi李建新
Yun-Xiao Li(李云霄), Wen-Han Xi(西文翰), Zhao-Yang Dong(董召阳),Zi-Jian Yao(姚子健), Shun-Li Yu(于顺利),4,†, and Jian-Xin Li(李建新),4,‡
1National Laboratory of Solid State Microstructures and Department of Physics,Nanjing University,Nanjing 210093,China
2Nanjing University of Science and Technology,Nanjing 210094,China
3Department of Physics,Nanjing Normal University,Nanjing 210023,China
4Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China
Keywords: unconventional superconductivity,pairing mechanism,Fermi surface,three-orbital model
1.Introduction
In recent years, there has been a growing interest in the study of unconventional superconductivity (SC) in multi-orbital systems, including Fe-based superconductors,[1–7]Sr2RuO4,[8–14]vanadium-based kagome superconductors,[15–24]and Ni-based superconducting materials.[25–31]In these superconductors, the low-energy physical properties are mainly determined by the d-orbital electrons of the transition metal atoms.In real materials, the five d orbitals in these materials are no longer degenerate due to the tetrahedral or octahedral crystal fields, resulting in the triple-degenerate t2gorbitals and the double-degenerate egorbitals.In a tetrahedral crystal field,as is the case of iron-based superconductors, the energy of the t2gorbitals is higher than that of the egorbitals.Conversely, in an octahedral crystal field, such as in Sr2RuO4, the energy of the egorbitals is higher than that of the t2gorbitals.As a result, for materials with a tetrahedral lattice structure, the low-energy physical properties are mainly governed by the t2gorbitals when the number of d electrons exceeds 4 per lattice site,such as in the iron-based superconductors.Similarly, for materials with an octahedral lattice structure,the low-energy physical properties are also dominated by the t2gorbitals when the number of d electrons is less than 6 per lattice site, such as in Sr2RuO4.Therefore, a systematic study of the superconducting pairing symmetry in the t2gthree-orbital models is important for understanding the superconducting mechanism of the superconductors dominated by electrons in d-orbitals.Moreover, the t2gorbitals also play a vital role in determining the low-energy physics of many magnetic materials, such as Na2IrO3[32–37]andα-RuCl3,[38–46]which have gained considerable attention in recent years.The realization of superconductivity in these materials through doping is also a subject of interest in current experimental research.Thus,a systematic investigation of the superconducting pairing symmetry with respect to the doping levels and Coulomb interactions in the t2gthree-orbital models can also provide valuable theoretical references for exploring new novel superconducting materials.
Many d-orbital superconducting materials exhibit a quasitwo-dimensional lattice structure.Due to the strong directionality of the t2g(dxy,dxzand dyz)orbitals,the hopping integrals of these orbitals are anisotropic within the two-dimensional plane.For instance, in Sr2RuO4,[47]the dxzand dyzorbitals have highly anisotropic hopping integrals, approaching zero for dxzin theydirection and dyzin thexdirection, which gives rise to quasi-one-dimensional properties.By contrast,the iron-based superconductors lack such strong anisotropy in the dxzand dyzhopping integrals, exhibiting quasi-twodimensional properties.Consequently, t2gthree-orbital models can be divided into two groups based on the quasi-onedimensional or quasi-two-dimensional characteristics of the dxzand dyzorbitals.The superconducting pairing symmetry of the latter group has been extensively studied across a broad range of doping levels (from electron to hole doping) in the context of iron-based superconductivity.[48–54]In contrast,the evolution of superconducting pairing symmetry with electron concentrations in the former group has not been explored, as Sr2RuO4only involves a fixed electron concentration.Investigating the electron-density dependence of the pairing symmetry in the related model will help supplement our understanding of the superconducting mechanism in the d-orbital systems.
In this paper, we employ the fluctuation exchange approximation(FLEX)method to perform a comprehensive and systematic investigation of the evolution of superconducting pairing symmetry with respect to the carrier density and interaction parameters in the t2gthree-orbital model, where the dxzand dyzorbitals exhibit quasi-one-dimensional characteristics.Despite the tight-binding parameters of the model being based on Sr2RuO4, our study systematically explores the influence of carrier density and interactions on the evolution of superconducting pairing symmetry,which makes our findings applicable to a wider range of material systems.When the Hund’s couplingJis at a moderate level relative to the Hubbard interactionU(aroundJ=0.25U), the superconducting pairing symmetry is mainly mediated by spin fluctuations and the system shows a strong preference for the spin-singlet pairing with a dx2−y2-wave throughout the entire particle concentration range we considered(n=1.5–4 per site).Furthermore,we find that a decrease inJleads to an enhancement of the charge fluctuations, resulting in a transition of the most favorable superconducting pairing symmetry from spin-singlet dx2−y2-wave to spin-triplet p-wave.We find that the superconducting pairings are orbital dependent.As the particle concentration changes fromn=4 ton=1.5, the active orbitals for superconducting pairing shift from the quasi-two-dimensional orbital dxyto the quasi-one-dimensional orbitals dxzand dyz.Our studies uncover detail evolutions of the superconducting pairing symmetries in the t2gthree-orbital model,and provide an insight to understand and explore the related material systems.
The paper is organized as follows.Section 2 introduces the three-orbital Hubbard model and the FLEX method.Section 3 presents the theoretical results and discussions.Finally,Section 4 provides the summary.
2.Model and method
The Hamiltonian of the t2gthree-orbital Hubbard model is given by

We carry out the investigation of the superconducting pairing symmetry by using the FLEX method[49,56–63]which is a self-consistent conserving approximation that is well-suited to the scenario of superconductivity mediated by spin and charge fluctuations.Since we adopt the three-orbital model,all the physical quantities below are matrices.[57]The renormalized Green’s functionG(k) is obtained from the Dyson equation
where the bare Green’s functionG(0)(k)−1is
and the self-energyΣ(k)is given by
Under the FLEX approximation, the effective interactionVnµ,mνis expressed as

and correspondingly the spin and susceptibility are
The electron density is determined byIn the above equations,k ≡(k,iωn)andq ≡(q,iνn)are used,whereωn=(2n+1)πTandνn=2nπTdenote the Matsubara frequencies for fermions and bosons, respectively.In the following calculations,we will use 32×32 meshes in the momentum space,8192 Matsubara frequencies andT=0.01.
After obtaining the renormalized Green’s function through a self-consistent solution of Eqs.(2)–(8), the superconducting pairing functions are determined by solving the Eliashberg equation
where the effective pairing interactions in the spin-singlet and spin-triplet channels respectively are
The eigenvectorψ(k)with the largest eigenvalueλgives the most favorable superconducting pairing.
3.Result and discussion
3.1.Evolution of pairing symmetry with electron concentration
In our calculations, we have chosen the Hubbard interaction parameterU= 1.5.We have verified that altering the value of HubbardUdoes not result in qualitative changes in the main physical quantities (see Fig.A1 in Appendix A).Hence, this moderate level of interaction is sufficient for our theoretical analysis.Additionally, for the electron concentration ofn=4, matching that of Sr2RuO4,we are able to reproduce the spin susceptibility with a peak at (2π/3,2π/3) (Fig.A1), which is consistent with the experimental observations[64,65]and previous theoretical calculations.[66–73]Based on our method and model parameters, the leading superconducting pairing symmetry exhibits a dx2−y2-wave structure (Fig.A1), aligning with prior theoretical findings on the spin-fluctuation-mediated pairing for a dominant incommensurate antiferromagnetic (2π/3,2π/3)spin fluctuation.[71–74]However, the spin susceptibility also exhibits broad and prominent weights at lowqand around(π,π).These features give rise to multiple competing superconducting pairing states and lead to variations in the most favorable state depending on the specific models utilized.[66–75]Thus,we can anticipate that the superconducting pairing states in our model will undergo changes in response to variations in particle concentration and interaction parameters.
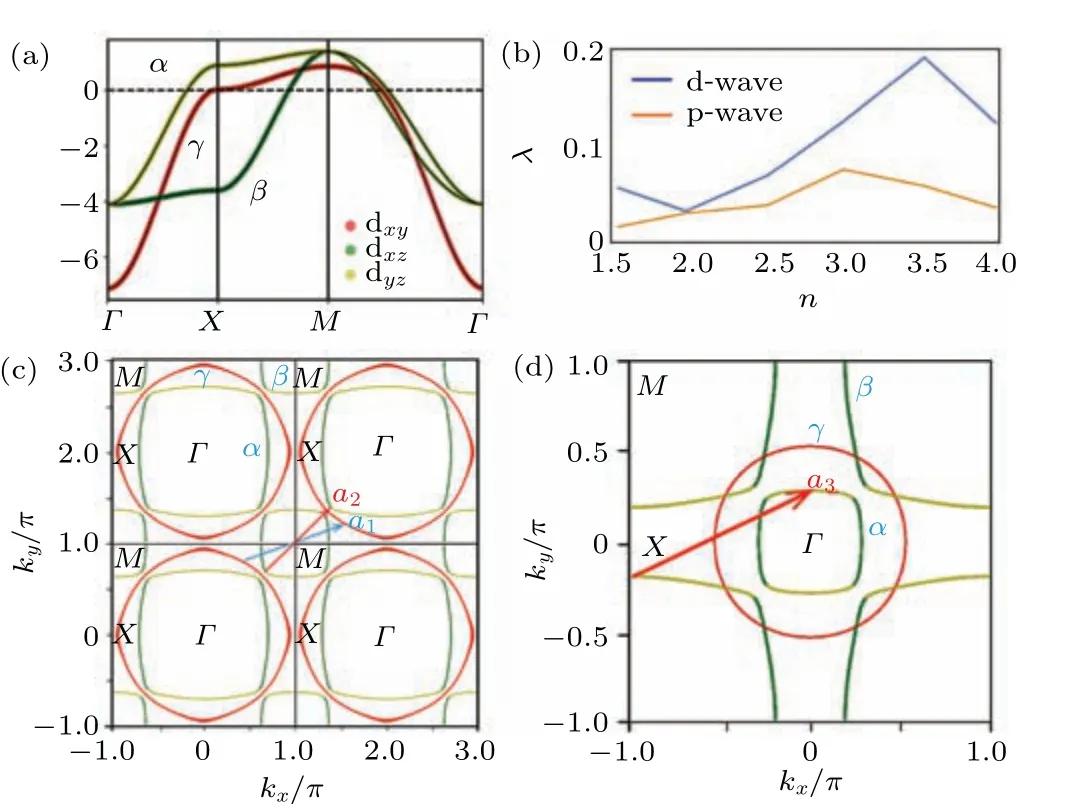
Fig.1.(a) Energy band for (t1,t2,t3,t4,λ,Δ,µ0)=(1.0,0.395,1.25,0.125,0.1,0.2,1.35).(b) Evolutions of maximum eigenvalues of Eq.(9)in both the spin-singlet and spin-triplet channels for J=0.25U.(c)Fermi surface for n=4.(d)Fermi surface for n=1.5.The arrows in(c)and(d)represent the nesting wavevectors.
Let us begin by discussing the evolution of superconducting pairing symmetry with particle concentration.In this analysis, we fix the Hund’s coupling to a moderate strength, i.e.,J=0.25U.As depicted in Fig.1(b),across the range of particle concentrations fromn=4 ton=1.5,the maximum eigenvalue in the spin-singlet channel consistently surpasses that in the spin-triplet channel, suggesting a preference for the spinsinglet pairing symmetry forJ=0.25U.To further investigate the pairing symmetries and understand their origins, we will examine the characteristics of the pairing function associated with the maximum eigenvalue.The pairing function matrix comprises nine (3×3) components.However, our numerical results indicate that the non-diagonal elements can be considered negligible since their values are nearly zero.[76]Consequently, our discussion will primarily focus on the diagonal components of the pairing functions, namely,ψ11,ψ22, and
ψ33.
The pairing functions for two typical particle concentrations, namely,n=4 andn=1.5, are shown in Fig.2.It can be observed that the superconducting pairing is orbital dependent.In the case ofn=4, the pairing strength of the dxyorbital surpasses those of the other two orbitals by several times[Figs.2(a)–2(c)].This indicates that the superconducting pairing predominantly occurs in the quasi-two-dimensional dxyorbital,which serves as the active orbital for superconductivity.Due to the absence of hybridization between dxyand dxz/dyzorbitals,the pairing strengths on the passive orbitals(dxzand dyz)are considerably weaker.In contrast,forn=1.5[Figs.2(d)–2(f)],the active orbitals shift to the dxzand dyzorbitals,which exhibit significantly larger pairing strengths compared to the dxyorbital.For both particle concentrations,the pairing functions satisfy the d-wave symmetry, albeit with notable differences in their specific forms.
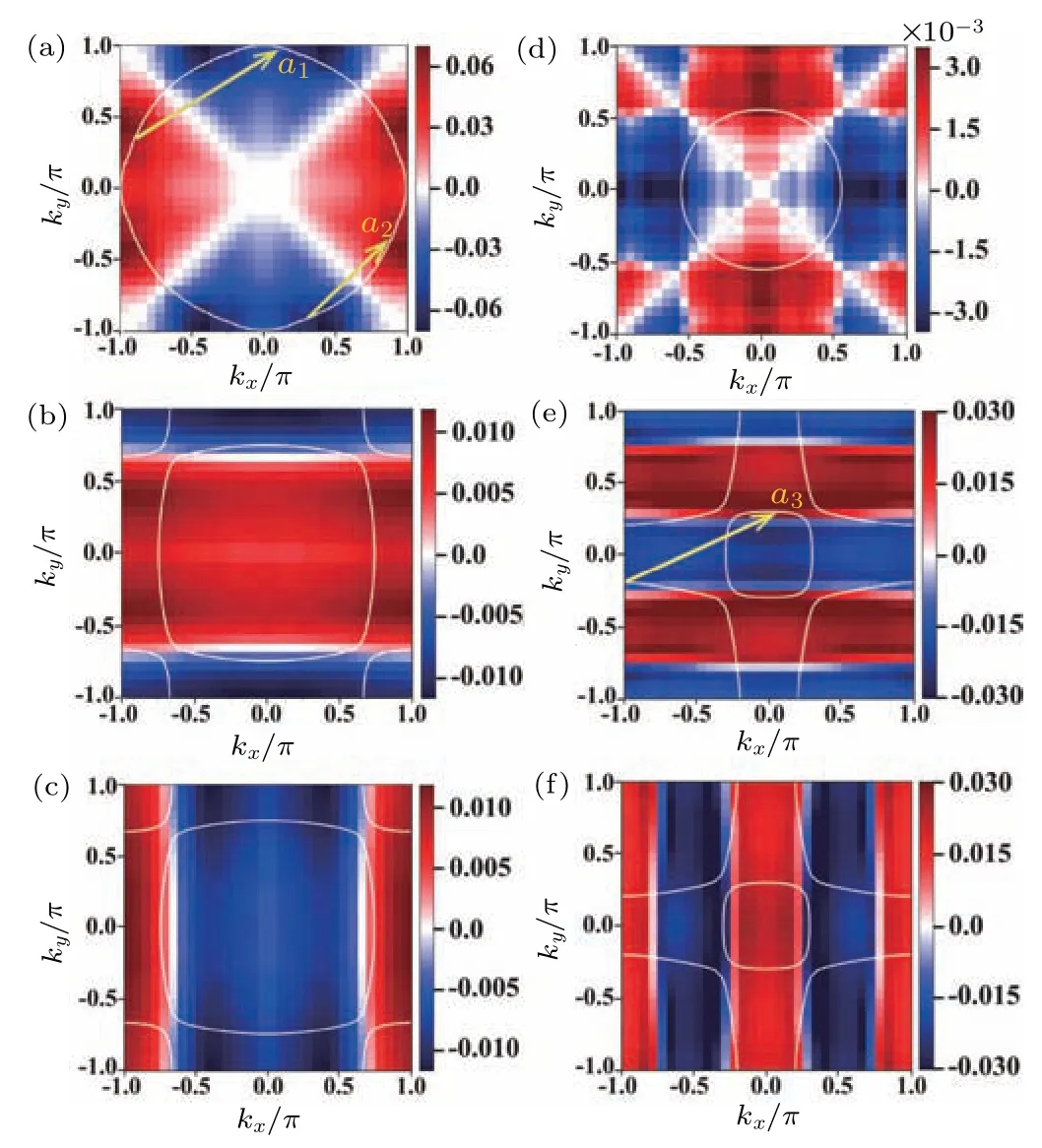
Fig.2.Pairing functions for n=4(left panel)and n=1.5(right panel)with J=0.25U.(a)and(d)ψ11.(b)and(e)ψ22.(c)and(f)ψ33.The white lines in(a)and(d)are the Fermi surfaces of the γ band,and those in(b),(c),(e),and(f)are the Fermi surfaces of the α and β bands.The arrows in (a) and (e) connect two regions on the Fermi surface where the pairing functions change sign and exhibit significant intensity.
In the case ofJ= 0.25U, the spin susceptibilities are significantly larger than the charge susceptibilities.[76]Consequently, according to Eqs.(10) and (11), the pairing interactions are primarily influenced by spin fluctuations, and the spin-singlet pairing interaction is much stronger than the spintriplet pairing interaction.This disparity explains the preference for spin-singlet superconductivity over spin-triplet superconductivity within the studied range of particle concentrations.To account for the origin of the pairing symmetry and its evolution with particle concentration, we will analyze the characteristics of spin susceptibilities.The distributions of the largest eigenvalues of the spin susceptibility tensorχ(k)are presented in Fig.A2.However, to analyze the origin of superconducting pairing symmetry, it is essential to consider the structure of each component.While the majority of the 81 components ofχ(k) exhibit negligible values,[76]we can focus on the components with the highest intensities.
Figures 3(a)–3(c) display the spin susceptibility componentsχs1111,χs2222, andχs2323forn=4.It is evident that the maximum value ofχs1111is approximately 2–5 times larger than those of the other components, which is the main factor that makes the dxyorbital the active orbital in superconducting pairing at this particle concentration.The characteristic wavevector ofχs1111is located ata1=(π,π/2)[Fig.3(a)],corresponding to the nesting wavevectora1of the Fermi surface(FS) as shown in Fig.1(c).For the superconducting pairing mainly mediated by spin fluctuations, if the spin susceptibility is prominent around a special wavevectorQ, the pairing scatterings will be dominated by(k,−k)to(k+Q,−k −Q)through exchanging the spin fluctuations aroundQaccording to Eq.(9).Consequently,the pairing functionψ(k)must satisfy the conditionψ(k)ψ(k+Q)<0 in order to get the largest eigenvalue of Eq.(9), since the pairing interactionVsingis positive.In our case here, the conditionψ(k)ψ(k+a1)<0 should be satisfied first, so the sign of the pairing function changes between the two parts ofψ11connected by the wavevectora1, as shown in Fig.2(a).In addition, the two parts connected by wavevectora2inψ11also change sign[Fig.2(a)].However, there is no corresponding characteristic wavevectora2inχs1111.Instead, we can identify the corresponding wavevector in the spin susceptibility componentχs2222[Fig.3(b)].Indeed,according to Eq.(10),the pairing interactionfor the dxyorbital can be approximately written as
whereis just the result via rotating 90°of.This implies that the pairing interaction of dxyorbital also has contributions from spin fluctuations of the dxzand dyzorbitals.Therefore,the spin fluctuations in the passive orbitals dxzand dyzalso affect the sign structure ofψ11in the active orbital dxy.
A notable change in the spin susceptibility occurs as the particle concentration decreases ton=1.5 , as illustrated in Figs.3(d)–3(f).Specifically,the maximum values ofχs1111are approximately one-fifth of that atn=4, whereas the maximum value ofχs2222remains almost unchanged.This can be attributed to the fact that,atn=1.5,the FS of dxyorbital has already become a circle without a nesting structure[Fig.1(d)],leading to a substantial reduction in the intensity ofχs1111.In contrast,the nesting properties of the FS of dxzand dyzorbitals remain nearly unchanged at different particle concentrations[Figs.1(c)and 1(d)],explaining why the maximum values ofχs2222show only slight variations.At this lower particle concentration,the active orbitals for superconducting pairing have changed from dxyto dxzand dyz, which can be confirmed by comparing the intensities of the pairing functions in different orbitals[Figs.2(d)–2(f)].In addition,the peak ofχs2222locates at (π,π/2), labelled bya3in Fig.3(e).This peak originates from the nesting property of FS as shown in Fig.1(d), and it also determines the sign structures of the pairing functions[Fig.2(e)].
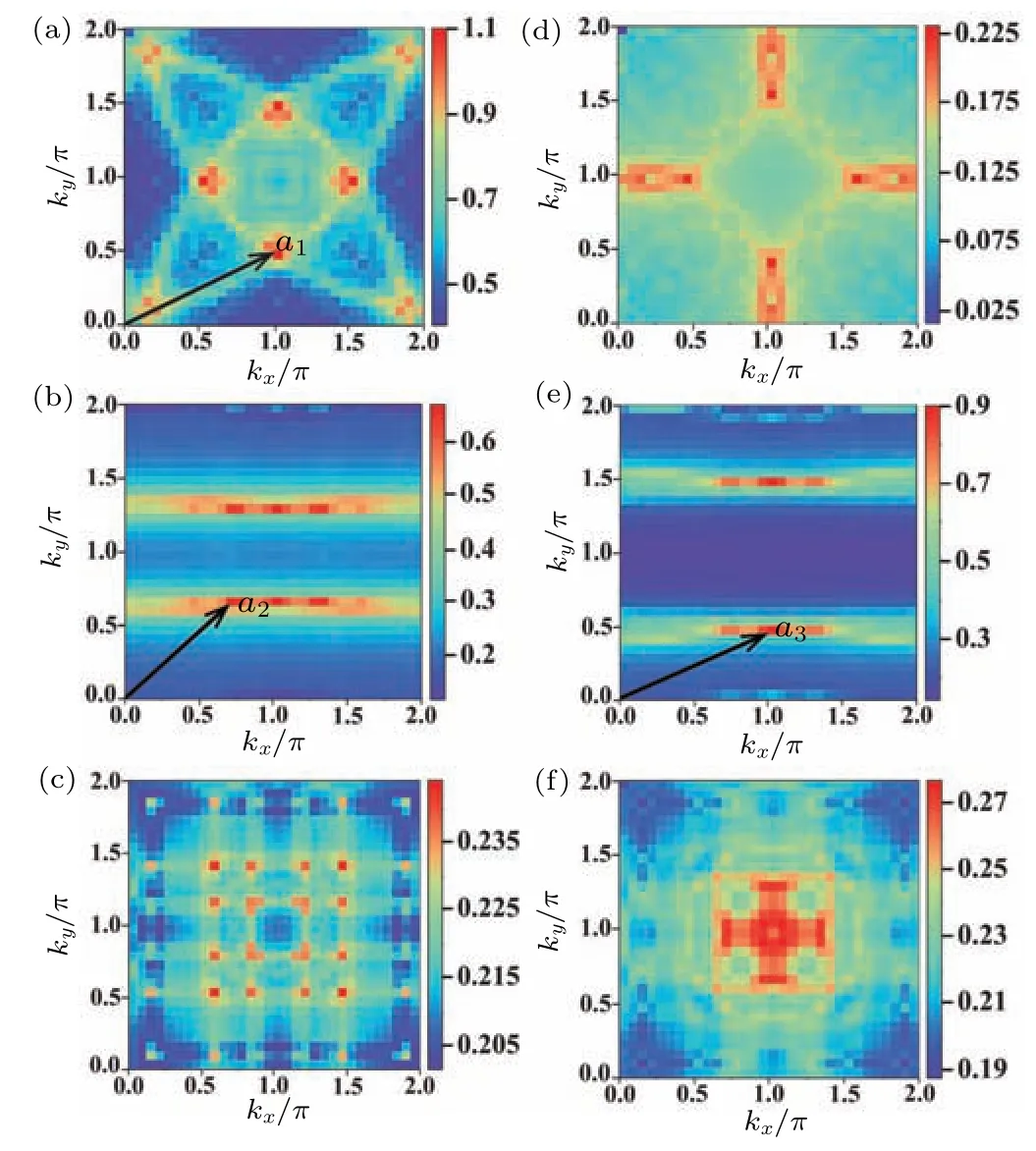
Fig.3.Spin susceptibilities for n=4 (left panel) and n=1.5 (right panel)with J=0.25U.(a)and(d)χs1111.(b)and(e)χs2222.(c)and(f)χs2323.The arrows represent the characteristic wavevectors of the peaks.
Furthermore, Fig.1(b) also exhibits a unique phenomenon: aroundn=2,the maximum eigenvalue in the spinsinglet channel decreases significantly, forming a minimum and nearly degenerating with that in the spin-triplet channel.As shown in Figs.4(a)–4(c), the dominant superconducting pairings are governed by the dxzand dyzorbitals atn=2, so we will focus on the pairing functionsψ22andψ33.This special phenomenon is still closely related to the characteristics of spin fluctuations.The main components of the spin susceptibility are shown in Figs.4(d)–4(f).We find that the maximum value ofχs2222is considerably greater than that ofχs1111,which is consistent with that the dxzand dyzare the active orbitals for superconducting pairing.The peak values ofχs2222exhibit a stripe-like distribution with little variation in intensity,which reflects the one-dimensional feature of the dxzorbital.Consequently, there exists a set of continuous characteristic wavevectors inχs2222.In Fig.4(e),we have plotted three representative wavevectorsa4,a5,anda6.According to the aforementioned discussion,the pairing functions on the FS coming from the dxzand dyzorbitals should satisfy the sign-changing conditionψ(k)ψ(k+Q)<0 as depicted in Fig.4(b).However, the momenta connected by these wavevectors almost form (k,−k) pairs, which requires the pairing functions to satisfyψ(k)=ψ(−k).This creates a contradiction between the sign structure required by the maximum eigenvalue and the fundamental requirements of singlet pairing.Due to the stripe feature of the peak distribution of the spin susceptibility,such contradictions occur at multiple continuous momentum points,resulting in a significant decrease in the eigenvalue in the spinsinglet channel.This also explains why the pairing intensities near the FS are almost zero[Figs.4(b)and 4(c)].Additionally,the inter-orbital sign structure of the pairing functions between the dxzand dyzorbitals[Figs.4(b)and 4(c)]is determined by the peak of the inter-orbital spin susceptibilityχs2323located ata7=(π,π)[Fig.4(f)].Although the spin-singlet pairing is always more favorable than the spin-triplet pairing in the case ofJ=0.25U,the near degeneracy of the two pairing types atn=2 suggests that adjusting other model parameters is highly likely to enable the spin-triplet pairing.

Fig.4.Pairing functions (left panel) and spin susceptibilities (right panel) for n=2 with J =0.25U.(a) ψ11, (b) ψ22, (c) ψ33, (d) χs1111,(e) χs2222, (f) χs2323.The white lines indicate the Fermi surfaces.The arrows in (b) represent the nesting wavevectors, and the arrows in (e)and(f)represent the characteristic wavevectors of the peaks of the susceptibilities.
3.2.Impact of interactions on pairing symmetry
As mentioned above, there exists a significant competition between singlet and triplet pairings in the model under investigation.Therefore, by adjusting the interaction parameters, there is a potential for realizing spin-triplet superconductivity.Next, we will investigate how the variation of the Hund’s coupling, namelyJ, influences the pairing symmetry.Figure 5(a) depicts the evolution of pairing symmetries with respect toJin both the spin-singlet and spin-triplet channels atn= 2.We find that the most favorable pairing symmetries in the spin-singlet and spin-triplet channels are d-wave and p-wave, respectively.Furthermore, we find that the spinsinglet superconductivity is more easily achieved with a largeJ, while the spin-triplet superconductivity is favored with a smallJ,with the phase transition between them occurring nearJ=0.25U.
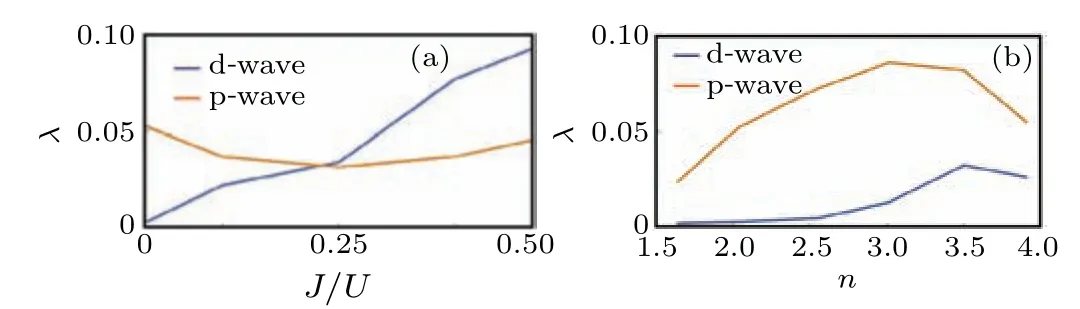
Fig.5.(a)Evolutions of the maximum eigenvalues of Eq.(9)with J for n=2.(b)Evolutions of the maximum eigenvalues of Eq.(9)with n for J=0.
Due to the constrain of the relationshipU=U'+2J, a decrease ofJcorresponds to an increase of the interorbital Coulomb interactionU', which is directly associated with charge density fluctuations,so reducingJcan enhance the role of charge fluctuations in driving superconducting pairing interactions.According to Eqs.(10)and(11),an increase in charge fluctuations will effectively reduce the spin-singlet pairing interactions but enhance the spin-triplet pairing interactions.To illustrate this more clearly, we present in Fig.5(b) the evolution of pairing symmetry with the particle concentration,considering the extreme case ofJ= 0.Remarkably, the spintriplet pairing emerges as the dominant pairing across the entire range of particle concentrations under studied.However,we find that although charge fluctuations do increase with the decrease ofJ, the peak of charge susceptibility remains consistently smaller than that of spin susceptibility.[76]Therefore,we will further analyze the contributions of spin fluctuations and charge fluctuations to pairing interactions through analytical calculations.
For the three-orbital model,both the spin and charge susceptibilities are represented by matrices of size 9×9, with 81 components,making analytical calculations quite cumbersome.To simplify the calculations,we will instead consider a two-orbital system that exhibits the same physics as the threeorbital system.[76]In order to further simplify the analysis,we focus on the limiting case ofJ=0, accordinglyU'=U.In this scenario,the interaction matricesUsandUcare
Furthermore, since many components of the spin and charge susceptibilities are nearly zero,[76]we only consider the most significant components, approximating the spin and charge susceptibilities as
By incorporating the above results into Eqs.(10) and (11),we express the effective pairing interactions in the spin-singlet and spin-triplet channels as
where
In the matrixΓc, the componentsα,β,γ,δandηrepresent the charge susceptibility componentsand,respectively.It is evident that when the charge susceptibility components become comparable to,but not necessarily exceeding, the spin susceptibility components, the effective pairing interactionVtripin the spin-triplet channel will surpassVsingin the spin-singlet channel.Consequently, the spin-triplet superconductivity becomes more favorable than the spin-singlet superconductivity.
When the spin-triplet pairing predominates in this system, the most favorable pairing symmetry is consistently in the form of p-wave over the entire range of particle concentrations we investigated.Moreover, as shown in Fig.6, forn=4, the superconducting pairing is primarily driven by the dxyorbital, while forn=1.5, the active orbitals are dxzand dyz.Hence, similar to the case ofJ= 0.25U, the system undergoes a transition from a quasi-two-dimensional orbital dxy-dominated pairing state to a pairing state dominated by two quasi-one-dimensional orbitals dxzand dyz,as the particle concentration varies.For the p-wave pairings, the Eliashberg equation(9),a linear gap equation,yields two degenerate solutions with pxand pysymmetries,both belonging to the same irreducible representation of the system’s symmetry group.In our calculations, the magnitude of each p-wave pairing and their relative phase cannot be determined, as they are determined by nonlinear effects.However, it is reasonable to expect that, in order to minimize the condensation energy, the system will spontaneously break the time-reversal symmetry and form a full-gaped px+ipypairing.
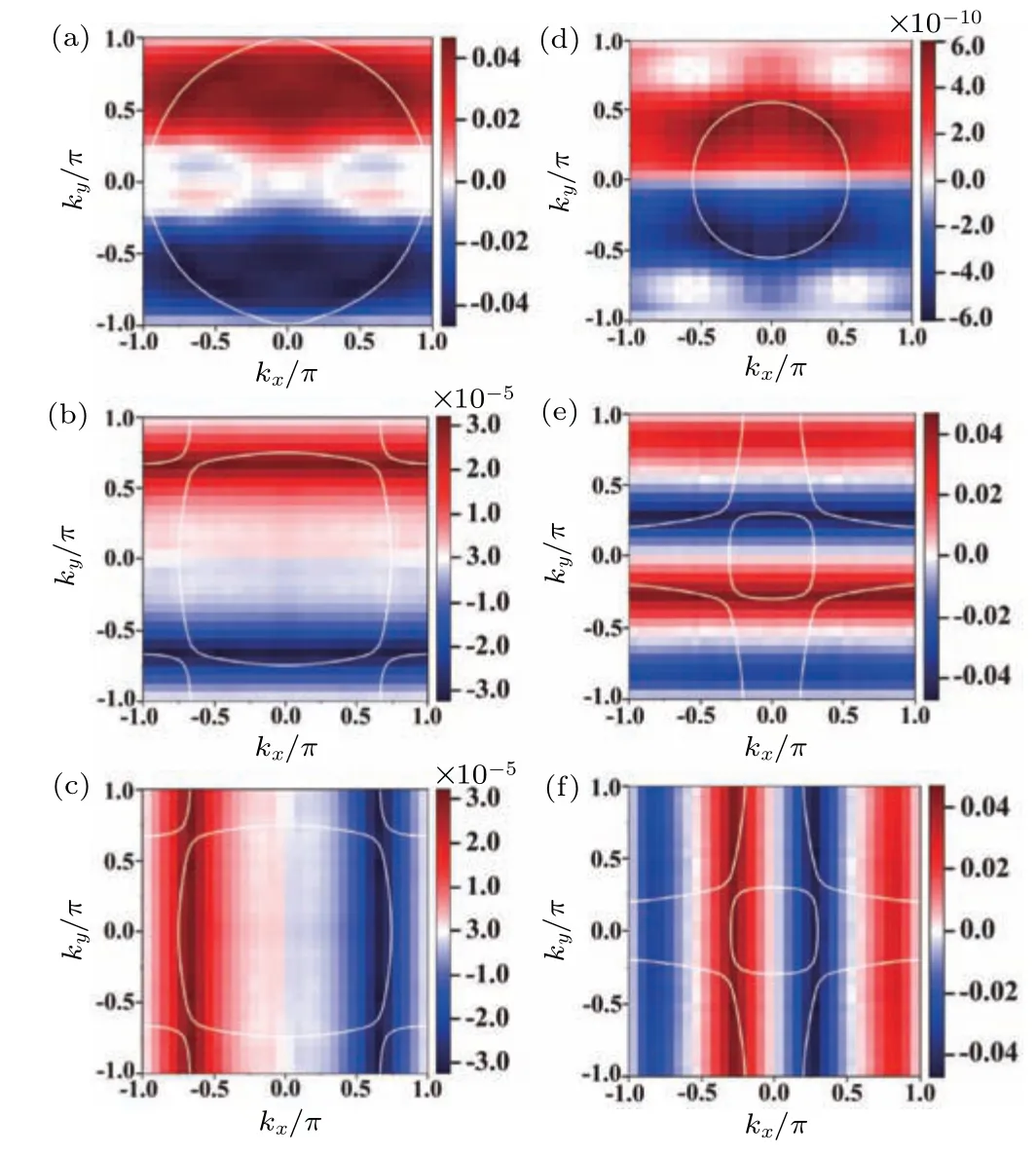
Fig.6.Pairing functions for n=4(left panel)and n=1.5(right panel)with J=0.(a)and(d)ψ11.(b)and(e)ψ22.(c)and(f)ψ33.
4.Summary
In summary,we have employed the FLEX method to investigate the evolution of superconducting pairing symmetry in a t2gthree-orbital Hubbard model on the square lattice,considering various particle concentrations and interaction parameters.For moderate levels of Hund’s coupling (J=0.25U),spin fluctuations dominate the superconducting pairing, leading to a prevalent spin-singlet pairing with dx2−y2-wave symmetry for all the particle concentrations that we have considered (n=1.5–4).By reducingJto enhance charge fluctuations, we find that the superconducting pairing symmetry changes from spin-singlet dx2−y2-wave to spin-triplet p-wave.These findings highlight the significant role of charge fluctuations in the superconducting mechanism of this three-orbital model.Moreover,regardless of whether it is a spin-singlet or spin-triplet pairing, we observe a shift of the active orbitals from the quasi-two-dimensional orbital dxyto the quasi-onedimensional orbitals dxzand dyzas the particle concentration varies fromn=4 ton=1.5.
Appendix A: Results for different Hubbard interactions and distributions of the largest eigenvalues of χs
In this appendix, to demonstrate that changing the value ofUwithin a certain range does not qualitatively affect our theoretical results, we present the spin susceptibilities and pairing functions for two representative values ofU(U=1.0 andU=2.0)atn=4 in Fig.A1.It is evident that the structures of the spin susceptibilities and pairing functions exhibit a high degree of consistency,with only minor variations in intensities.Therefore, the selection ofUdoes not qualitatively impact our conclusions.We also observe that within the fluctuation exchange approximation, the superconducting pairing symmetry of our model atn=4 is a singlet d-wave, which may be helpful for understanding the current experimental observations of singlet superconductivity in Sr2RuO4.
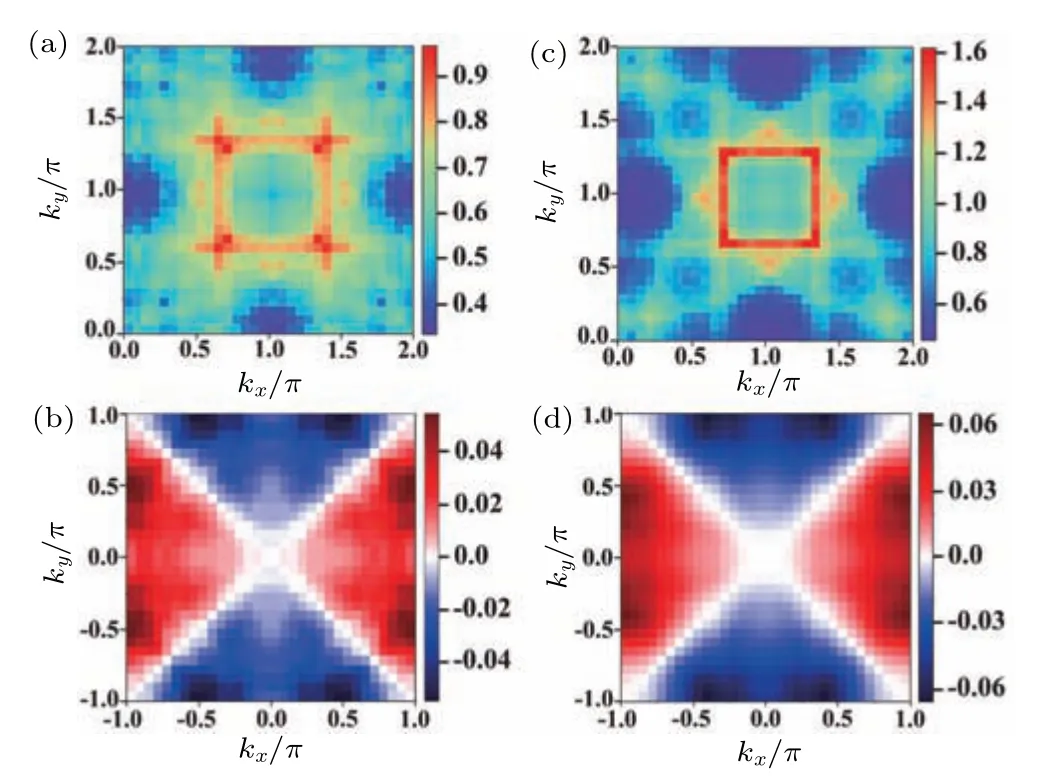
Fig.A1.Distributions of the largest eigenvalues of the spin susceptibilities χ(k)and pairing functions for U =1(left panel)and U =2(right panel)with the Hund’s coupling J=0.25U.(a)and(c)χs.(b)and(d)ψ11.
The distributions of the largest eigenvalues of the susceptibility shown in Fig.A2 are related to Figs.3 and 4 forn=1.5 andn=2.0,respectively.
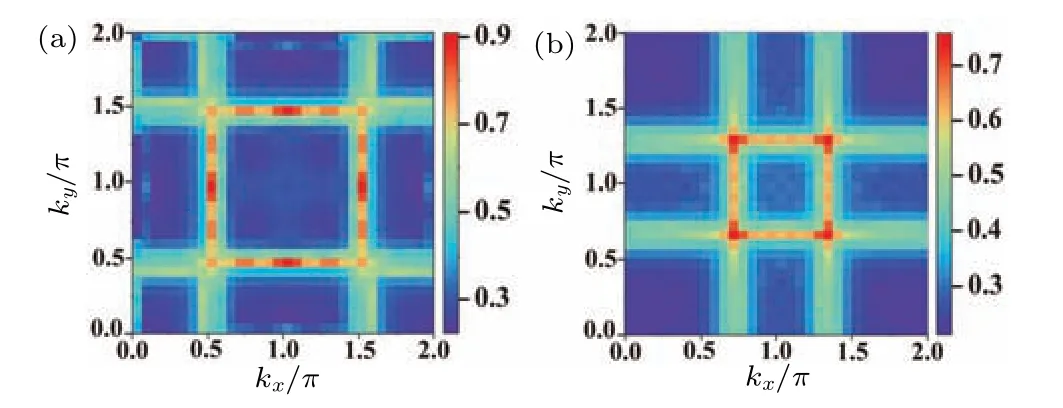
Fig.A2.Distribution of the largest eigenvalues of the spin susceptibility χ(k)for U =1.5 and J=0.25U.(a)n=1.5.(b)n=2.0.
Data availability statement
The data that support the findings of this study are openly available in Science Data Bank at https://doi.org/10.57760/sciencedb.j00113.00182.
Acknowledgements
Project supported by the National Key Research and Development Program of China (Grant No.2021YFA1400400)and the National Natural Science Foundation of China(Grant Nos.92165205,12074175,and 12374137).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals
