数控机床几何误差单轴五次测量与辨识方法*

季泽平,田春苗,郭世杰,2,唐术锋,2,兰月政,2*

(1.内蒙古工业大学 机械工程学院,内蒙古 呼和浩特 010051;2.内蒙古自治区特殊服役智能机器人重点实验室,内蒙古 呼和浩特 010051)

0 引 言

在数控机床的加工过程中,机床精度受到多种误差源的影响,其中几何误差和热误差约占总误差的70%[1],是机床误差的主要组成部分。几何误差与机床零部件的形位精度相关,重复性好、准静态特性强,且系统性高[2-3]。当环境温度变化较小时,几何误差对数控机床精度的影响会更加明显[4]136。因此,如何通过有效的误差测量手段得到几何误差的准确数值成为亟待解决的问题。

几何误差的测量方法一般可以分为两类:一类是以测量仪器为核心的直接测量法;另一类是以测量策略为核心的间接辨识方法[5]。其中,直接测量法操作简单、测量方便,即针对机床某项误差单独进行测量,进行相应误差项的分析补偿。常用的检测仪器包括激光干涉仪、电容式传感器、激光跟踪仪等。

CHEN Y T、LIU C X等人[6-7]研发出了一套高效便捷的几何误差测量系统,测量精度高、系统成本低。冯其波等人[8-11]研制出了保偏光纤耦合双频激光器,其可同时测量单轴6自由度几何误差。李津容等人[12]提出了一种在机测量线激光传感器安装位姿标定方法,建立了线激光在机测量系统的数学模型,并考虑了机床定位误差对标定结果精度的影响。

所谓间接辨识法,即是使用测量仪器对机床的综合误差进行测量,然后对其进行解耦,间接计算得到多项几何误差。常用方法包括标准圆轨迹测量辨识法[13-15]、激光跟踪仪多站测量法[16]、基于激光干涉仪的多线法[17]、体对角线法[18]、分布体对角线法[19]等。其中,基于激光干涉仪的九线法、十二线法、十三线法等测量线数过多,测量位置存在限制,不易于调整安装,多次安装设备会造成误差累计。对于单轴6项几何误差而言,其不可同时辨识得到,需通过上一个方程解得的误差数据求解下一个误差项;空间体对角线测量方法需假设角度误差较小,测量结果仅能作为机床精度的评价手段,不能准确辨识各个误差项;分步体对角线法测量路径较多,且测量过程中会耦合动态误差,辨识精度较低。

由此可见,已有的基于激光干涉仪的空间几何误差测量辨识方法在测量精度、测量效率、测量周期等方面难以兼顾,需进一步优化以解决目前存在的问题。

为完善现有的激光干涉仪多线测量辨识方法,笔者提出一种基于激光干涉仪的机床空间几何误差单轴五次测量法。

首先,根据直线轴实际运动状态并结合激光干涉仪测量原理,分析测量过程中的误差耦合情况;然后,针对3个直线轴规划一条测量路径,采用单轴运动方式,在测量范围内测量3条划定线上除滚转误差外的其他15项几何误差;最后,依据误差辨识方程组,求解得到各运动轴的6项几何误差,并与空间九线法测量辨识结果对比,以验证单轴5次测量法的准确性、有效性。

1 几何误差项定义及整机误差建模

1.1 几何误差的定义

一个物体在空间运动有6个自由度,因此,当机床移动部件沿任一平动轴移动时都会产生6项误差元素。

以X轴运动为例,6项几何误差示意图如图1所示。

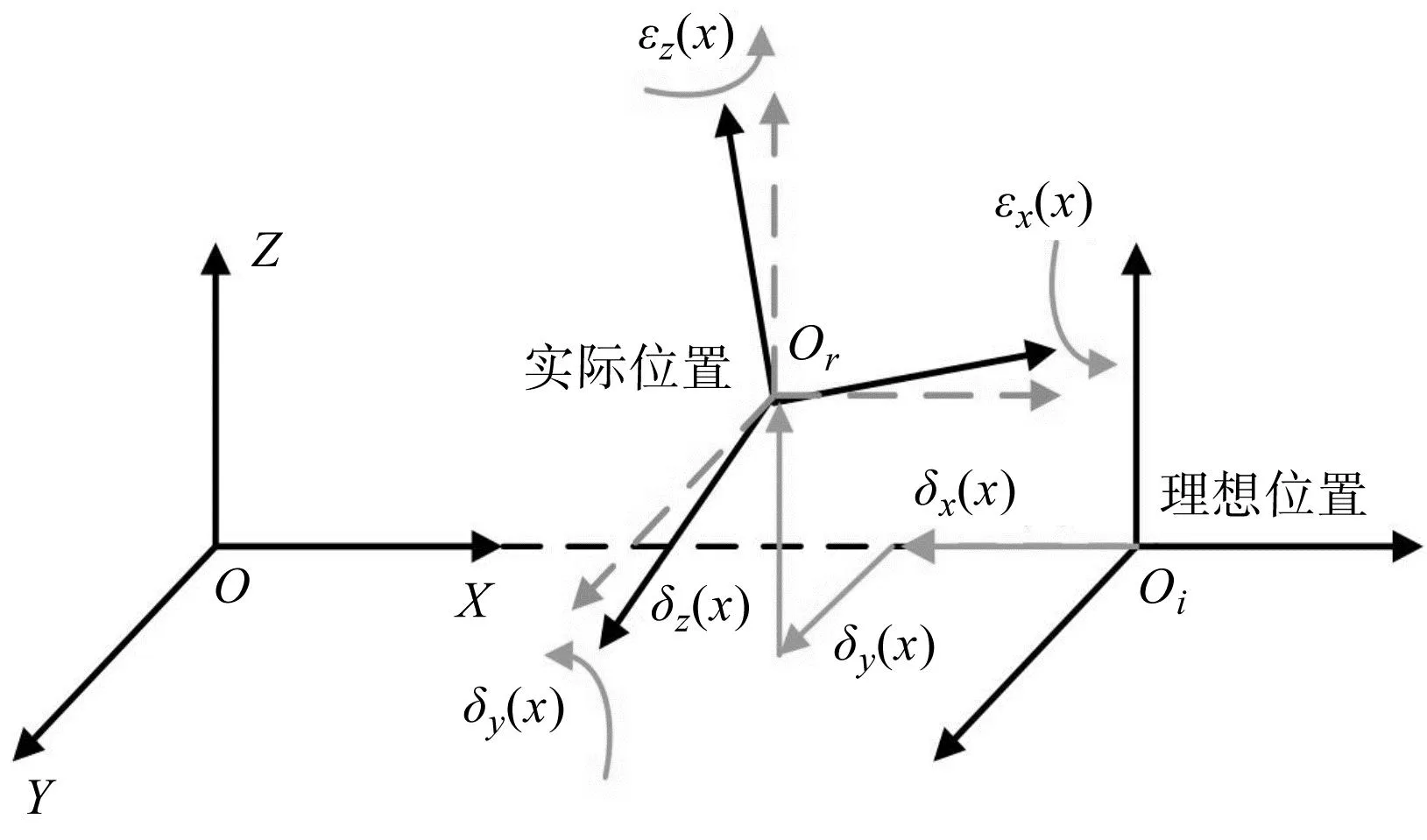
图1 X轴6项几何误差示意图Fig.1 Diagram of 6 geometric error elements in X-axis

工作台沿X方向运动一段距离后,由于几何误差的存在,实际到达位置与理想位置并不相同。产生的6项几何误差元素分别为:沿X方向的定位误差δx(x)、沿Y方向的水平直线度误差δy(x)、沿Z方向的垂直直线度误差δz(x)、绕X轴的滚转误差εx(x)、绕Y轴的俯仰误差εy(x)和绕Z轴的偏摆误差εz(x)。3个直线轴之间还会产生3项垂直度误差。

因此,三轴数控机床共存在21项几何误差元素,如表1所示。

1.2 机床结构及空间误差模型建立

三轴立式机床是一种典型的多体系统,由X轴、Y轴、Z轴导轨、工作台、刀具等多个运动部件组成,这些部件之间的运动轨迹相互关联。为了描述不同部件之间的位置关系,还需要建立各运动部件之间的坐标变换关系。

该实验研究对象为工业现场常用的XYTZ型(X、Y表示工件链、T表示机床床身、Z表示刀具链)三轴立式机床。

机床结构简图如图2所示。

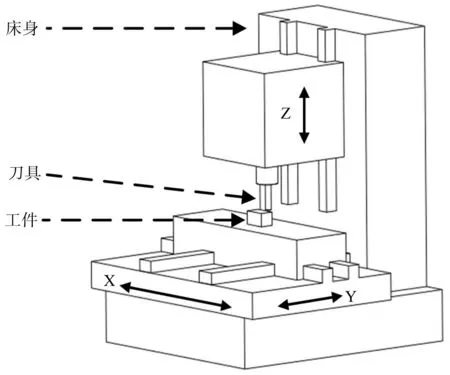
图2 XYTZ型机床结构简图Fig.2 XYTZ machine tool structure diagram

首先,笔者建立机床各运动部件的坐标系,并选取参考坐标系;其次,根据齐次坐标变换确定刀具链与工件链之间的联系;最后,依据运动传动关系得到刀尖点与工件理想的被加工点之间的偏差量,即可建立误差综合模型。

机床各部件坐标系如图3所示。

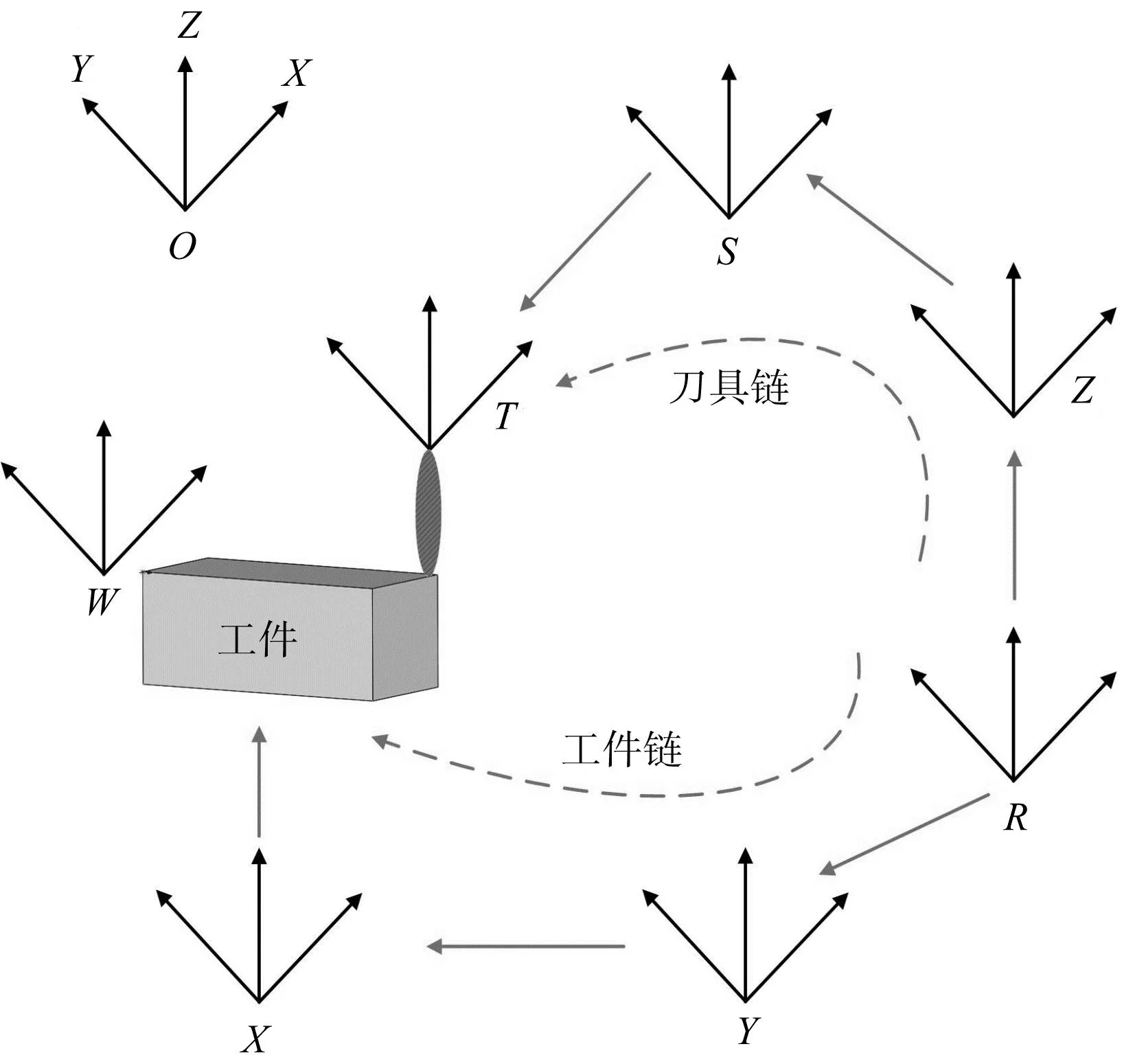
图3 机床各部件坐标系Fig.3 Coordinate system of machine tool componentsR为参考坐标系;X为X轴坐标系;Y为Y轴坐标系;Z为Z轴坐标系;S为主轴坐标系;T为刀具坐标系;W为工件坐标系。

对于三轴立式机床而言,加工时工件安放在工作台上,工作台可以沿X轴和Y轴移动;刀具安装在主轴上,主轴固定在Z轴上。这样的布局方式使得机床可以在X、Y、Z三个方向上进行高精度的切削加工。

理想状态下,刀尖点与工件切削点之间并无相对位置移动,刀具链和工件链可视为相对静止状态;在实际状态下,当X、Y、Z轴分别移动x、y、z距离时,工件切削点坐标可由工件链经齐次坐标变换,转换至参考坐标系R。刀尖点坐标可由刀具链经齐次坐标变换,转换至参考坐标系R。由于存在几何误差,二者不再重合,存在相对位置偏差。

依据多体系统理论和齐次坐标变换方法,可根据机床刀尖点坐标相对于工件切削点坐标的位置偏差,建立三轴机床的几何误差模型[4]137-138,如下式所示:

Δx=-δx(x)-δx(y)+δx(z)-y·εz(x)-z·
εy(x)-z·εy(y)+z·Sxz+yT·(εz(x)+εz(y)-
εz(z))-zT·(εy(x)+εy(y)-εy(z))

Δy=-δy(x)-δy(y)+δy(z)+x·εz(x)+z·
εx(x)+z·εx(y)+x·Sxy-z·Syz-xT·
(εz(x)+εz(y)-εz(z))+zT·(εx(x)+
εx(y)-εx(z))

Δz=-δz(x)-δz(y)+δz(z)-x·εy(x)+y·
εx(x)+y·εx(y)+xT·(εy(x)+εy(y)-εy(z))-
yT·(εx(x)+εx(y)-εx(z))

(1)

式中:xT,yT,zT为刀具坐标系下刀尖点坐标。

2 单轴五次测量及辨识方案

2.1 测量路径规划

单轴五次测量法测量路径如图4所示。

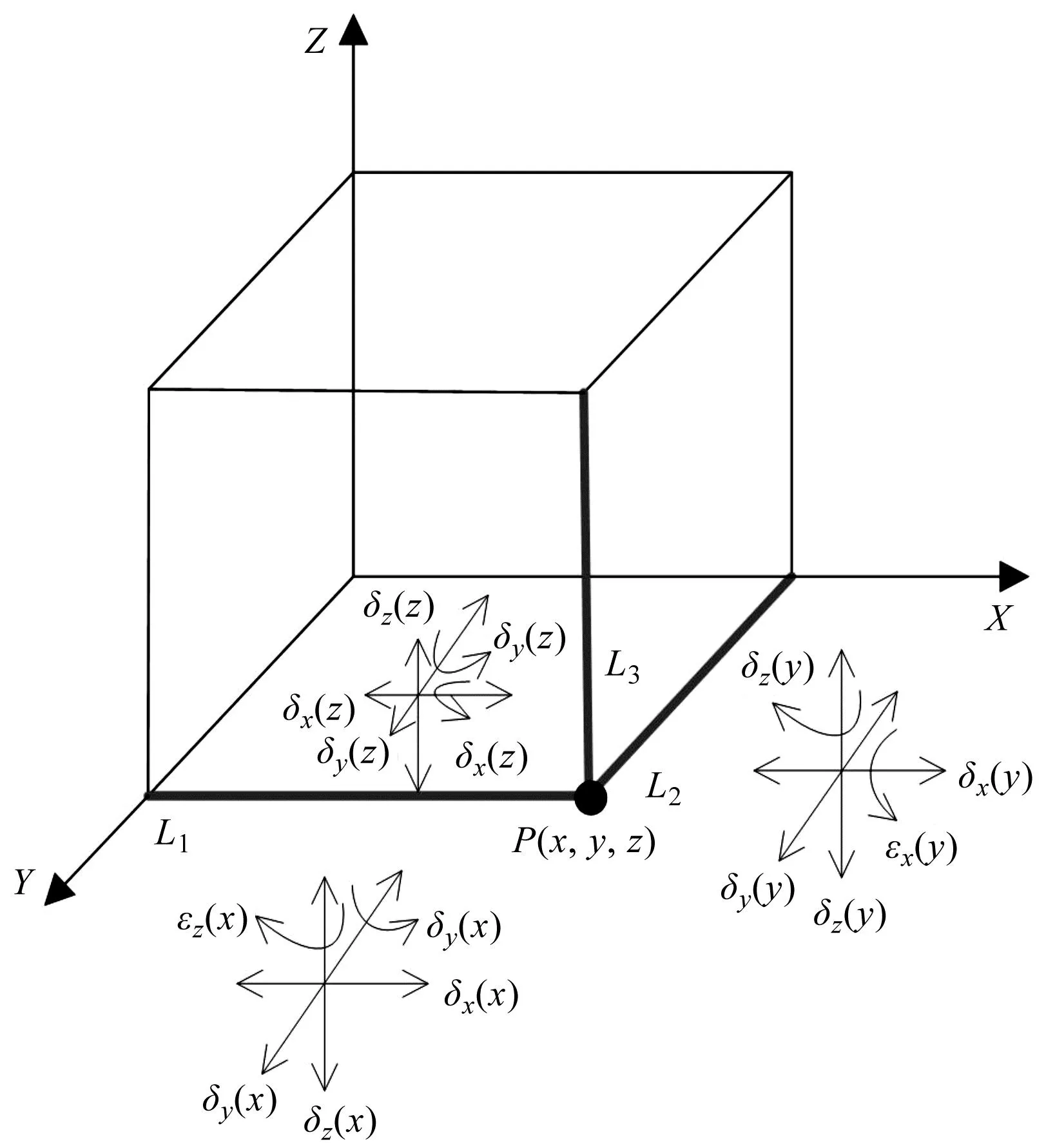
图4 单轴五次测量法路径规划Fig.4 Path planning of single-axis and five-times measurement method

首先,笔者在机床行程空间内选取一个测量点P(x1,y1,z1);其次,针对X、Y、Z方向分别设置一条测量线L1、L2、L3,采用单轴运动方式。分别测量3条划定线上的定位误差、水平直线度误差、垂直直线度误差、偏摆误差、俯仰误差,共计测量15次。

2.2 误差辨识流程

笔者根据激光干涉仪测量原理分析测量过程中的误差耦合情况,并建立误差辨识方程组;结合误差辨识方程组与测量数据,求解得到各运动轴的6项几何误差,针对每一项几何误差建立参数化模型曲线,可由误差曲线获得机床全测量行程内的误差信息。

单轴五次测量法辨识流程如图5所示。

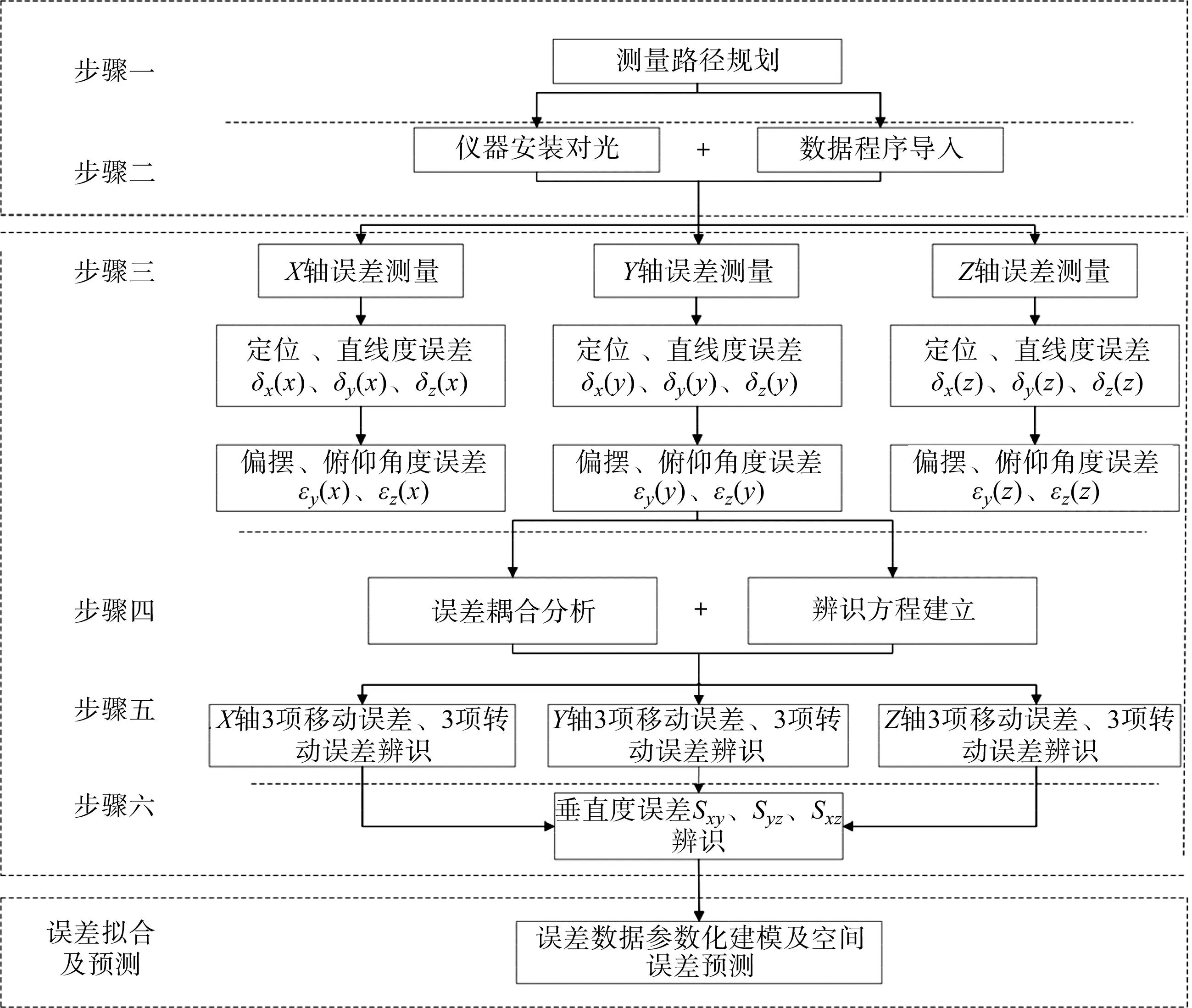
图5 单轴五次测量法辨识流程Fig.5 The process of measurement and identification with single-axis and five-times measurement method

2.2.1 误差耦合分量分析

1)转角误差与直线度误差耦合分析。笔者在测量水平轴垂直直线度误差时,根据干涉镜和反射镜安装时运动部分和固定部分的差异,发现存在两种不同的测量方式,如图6所示。

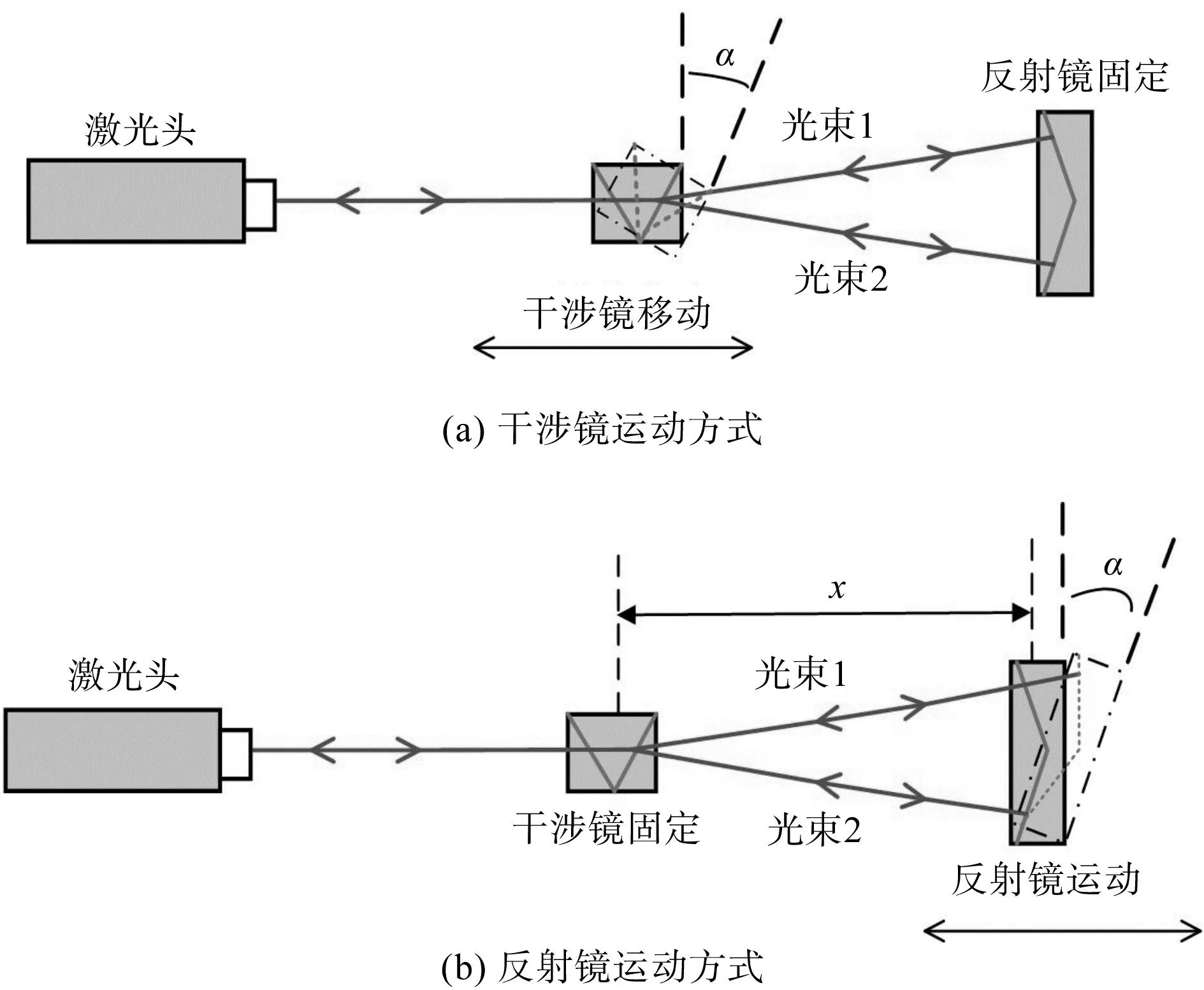
图6 激光干涉仪测量直线度时两种不同安装方式Fig.6 Two different installation methods for measuring straightness of laser interferometer

图6(a)中,若反射镜固定、干涉镜移动,由于干涉镜为沃拉斯顿棱镜,不受竖直方向的角度变化影响,因此直线度测量数据不含角度误差耦合分量。

图6(b)中,若采用干涉镜固定、反射镜移动方式,反射镜对于机床竖直方向产生的俯仰角度变化较为敏感,当反射镜产生一个极其微小的俯仰角度α时,光束1与光束2的长度也会发生相对变化。因此,直线度误差数据中会耦合一个非常小的非直线度数值,大小为光学镜组合之间的距离x与俯仰角度α的正切值的乘积[20]。因此,在测量过程中应选择干涉镜固定、反射镜运动的方式,不仅可利用测量数据对机床直线度误差进行补偿,同时也可为机床装配精度评估提供数据基础。

测量运动轴水平直线度时,笔者需将直线度反射镜水平放置,因此反射光束不受俯仰角度误差影响。测量数据可视为机床水平直线度的真实值,工作台沿X方向运动实际产生的水平和垂直直线度误差如下式所示:

(2)

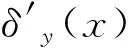
2)直线度误差与定位误差耦合分析。在水平轴运动过程中,工作台的两端由于自身重力作用会产生下沉,如图7所示。

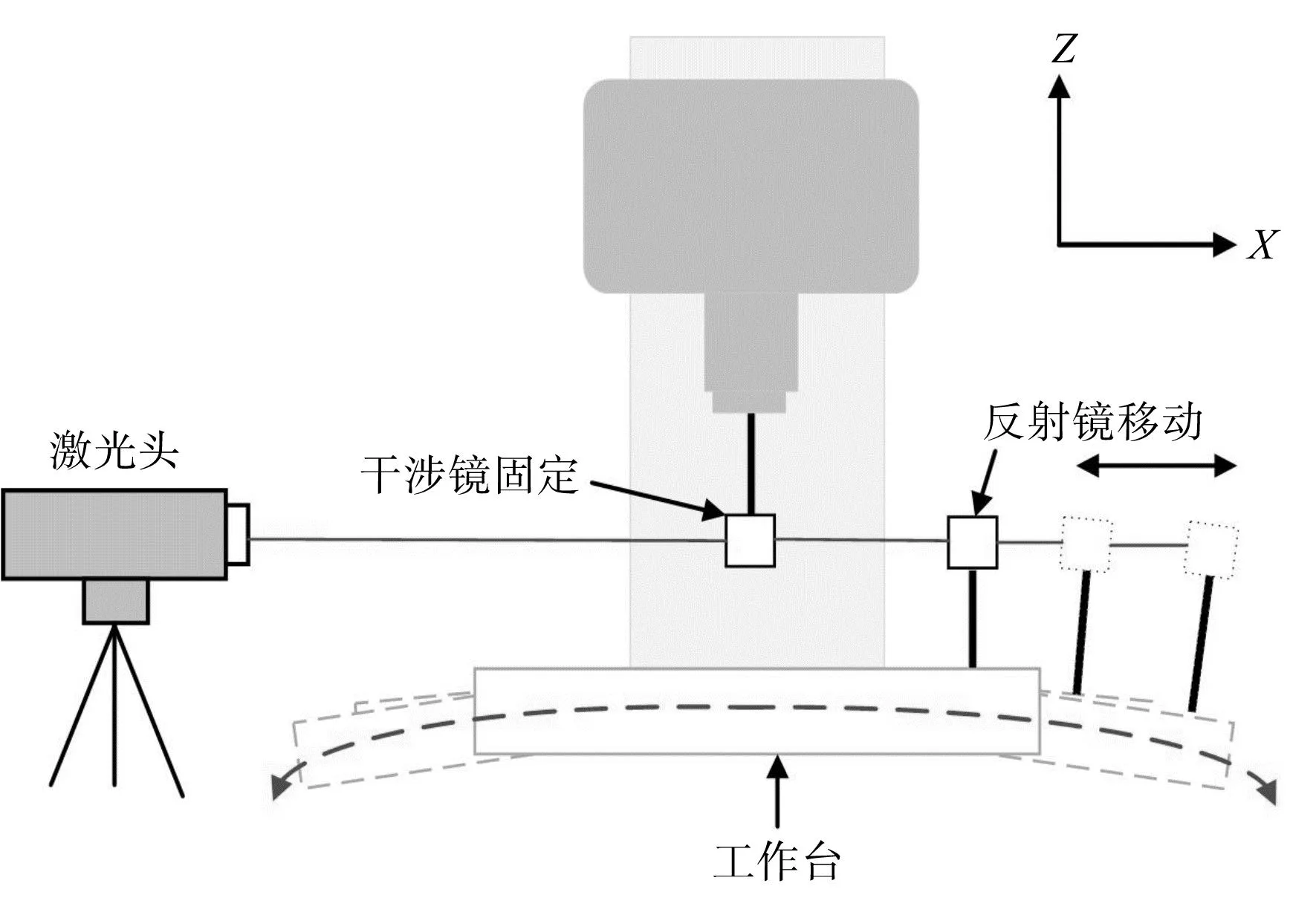
图7 工作台两端受重力作用下沉示意图Fig.7 Diagram of both ends of the table sinking under gravity

运动过程中,工作台会产生垂直于运动方向的直线度误差,这部分直线度误差会对定位误差产生影响[21],如图8所示。

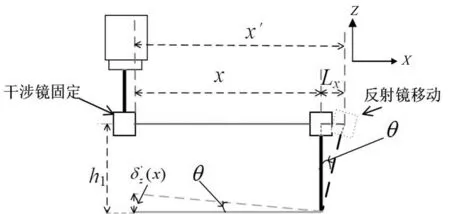
图8 直线度误差与定位误差耦合Fig.8 Coupling of straightness error and positioning errorX为机床的指令行程;x′为机床的实际行程;h1为测量点距离X轴平面的距离;δz(x)为X轴Z向直线度误差;θ为工作台的角度波动值;Lx为垂直直线度误差引起的定位误差耦合分量。

在X轴实际运动状态下,由于重力作用工作台两端会产生下沉,因此工作台与水平面会产生一个非常细微的偏差角θ。此时,激光干涉仪所测距离为x′,实际测量所得的定位误差数据包含X轴固有的定位误差δx(x)与Z向直线度引起的定位误差Lx两部分。

由图8中几何关系可知,θ与Lx如下式所示:

(3)

(4)

X轴固有的定位误差如下式所示:

(5)

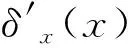
水平直线度误差是由于机床设计、装配等因素造成的几何误差,不受重力影响,因此对定位误差基本无影响。

在机床运行过程中,可视机床运动部件为刚体,因此在任一时刻内,机床运动部件上每一点处的偏摆误差和俯仰误差是相等的。此时,激光干涉仪测量所得的转角误差数据即可视为X轴的转角误差值。

2.2.2 辨识方程的建立

测量时,需要将移动镜组安装在工作台上设定的测量起点处,随运动轴一起运动,并需要建立两个坐标系,即运动轴坐标系和测量坐标系;通过不同坐标系下相同坐标点坐标之间的齐次坐标变换关系,计算得到线性误差辨识方程组。

三个直线轴的误差测量相互独立,互不影响,其辨识方程的建立方法也完全相同。

以X轴为例,坐标系示意图如图9所示。

图9 X轴坐标系与测量坐标系示意图Fig.9 X-axis coordinate system and measurement coordinate system diagram

在X轴坐标系Ox中,笔者选取一点a1作为原点,建立X轴测量坐标系Om,测量起点a2随X轴运动距离x后到达测量终点a3。(x1,y1,z1)为测量坐标系相对于X轴坐标系的偏移量、(x2,y2,z2)为测量坐标系下a2点的坐标、(x3,y3,z3)为测量坐标系下a3点的坐标。

设X轴的运动矩阵、测量坐标系相对于X轴坐标系的偏移矩阵、测量起点a2运动时,其产生的误差矩阵分别为Tx、Td、Ex,如下式所示:

(6)

(7)

(8)

1)测量坐标系下a3点与a2点的坐标变换关系如下式所示:

(9)

式中:上角标“T”为矩阵的转置;下角标“m”为测量坐标系;

2)X轴坐标系下a3点坐标与测量坐标系下a2点坐标变换关系如下式所示:

(10)

式中:下标x为X轴坐标系。

测量坐标系下a3点坐标与X轴坐标系下a3点坐标变换关系如下式所示(即将测量坐标系下a3点坐标左乘偏移矩阵Td):

(11)

将式(9)代入式(11),可知式(10)与式(11)左右两边相等,如下式所示:

Tx·Ex·Td=Td·Tx·Ex

(12)

计算式(12),可得X轴线性误差辨识方程组如下式所示:

(13)

2.2.3 几何误差项辨识

综合式(2)和式(13),并根据等价无穷小原则,可以推出X轴6项几何误差辨识方程组,如下式所示:

(14)

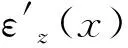
由式(14)可知,只要y1+z1≠0,则方程组就有解,即能够辨识出X轴的6项几何误差。

由X轴误差辨识原理可得Y轴6项几何误差如下式所示:

(15)

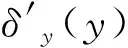
根据X轴几何误差辨识流程与原理,可得Z轴几何误差的辨识方程组如下式所示:

(16)

Z轴几何误差辨识流程和原理与X、Y轴相同,但Z轴作为垂直轴,在测量时,笔者需将反射镜组安装在主轴座上,随Z轴竖直运动。因其主轴座以及主轴箱重力原因,运动过程中,反射镜组存在下沉趋势,因此定位误差数据会比测量值略大。

垂直度误差则可以根据同一基准下测量直线度误差时的角度偏差,通过计算的方式得到。

至此,直线轴21项几何误差均已辨识完成。

3 实验验证

在该实验中,笔者选用的设备为VDL-600A三轴立式加工中心,其配备FANUC 0i高端数控系统,能够提供高精度的控制和操作界面,以确保加工过程的精确性和稳定性;三个运动轴均配备高精度滚珠丝杠副,保证了加工中心的定位精度和重复定位精度。

单轴五次法测量实验如图10所示。

图10 单轴五次测量法实验现场Fig.10 Single axis and five-times measurement method experimental field

根据机床行程和测量镜组不发生碰撞的条件,笔者确定了三个轴的测量范围:X轴为-210 mm～90 mm,Y轴为-160 mm～140 mm,Z轴为-150 mm～150 mm;测量点为机床行程空间内(-210,-160,-150),测量间隔均为15 mm,进给速度为1 000 mm/min;采用干涉镜静止、反射镜移动方式进行测量。

同时,笔者利用九线法在相同测量行程内进行几何误差测量和辨识。

九线法测量图如图11所示。

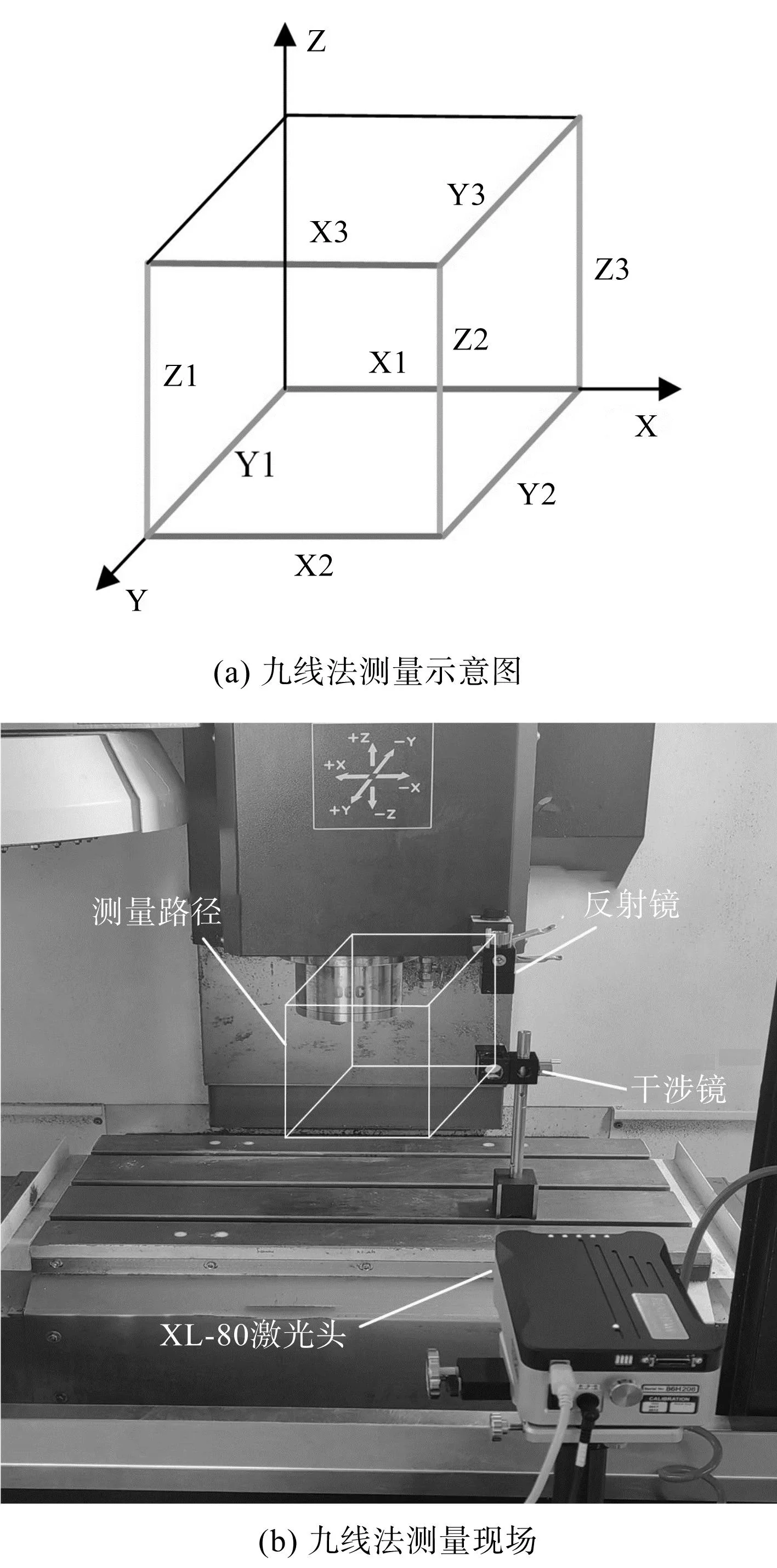
图11 九线法测量Fig.11 Nine-line method of measurement

九线法的基本思路为:在X、Y、Z三个运动轴的测量方向上选定3条测量直线,沿测量线方向和垂直于测量线方向测量机床的定位误差与直线度误差。

为便于后续与单轴五次测量法辨识结果进行对比,在使用九线法测量时,X、Y、Z三轴测量线中应分别包含单轴五次测量法所需的3条测量线。因此,相同测量线上的测量数据也完全相同。

九线法测量空间参数为:X轴测量范围为-210 mm～90 mm,Y轴测量范围为-160 mm～140 mm,Z轴测量范围为-150 mm～150 mm;测量间隔均为15 mm,对X轴上的3条直线(直线X1:(x,-160,-150)、直线X2:(x,0,-150)、直线X3:(x,140,150)),Y轴上的3条直线(直线Y1:(90,y,-150)、直线Y2:(-210,y,-150)、直线Y3:(-210,y,150)),Z轴上的3条直线(直线Z1:(90,140,z)、直线Z2:(-160,140,z)、直线Z3:(-210,-160,z))上的定位误差与直线度误差进行测量。

笔者往复测量3次,并求取平均值,然后分别采用单轴五次测量法与九线法辨识原理对测量数据进行辨识。

X、Y、Z轴18项几何误差对比曲线如图12所示。

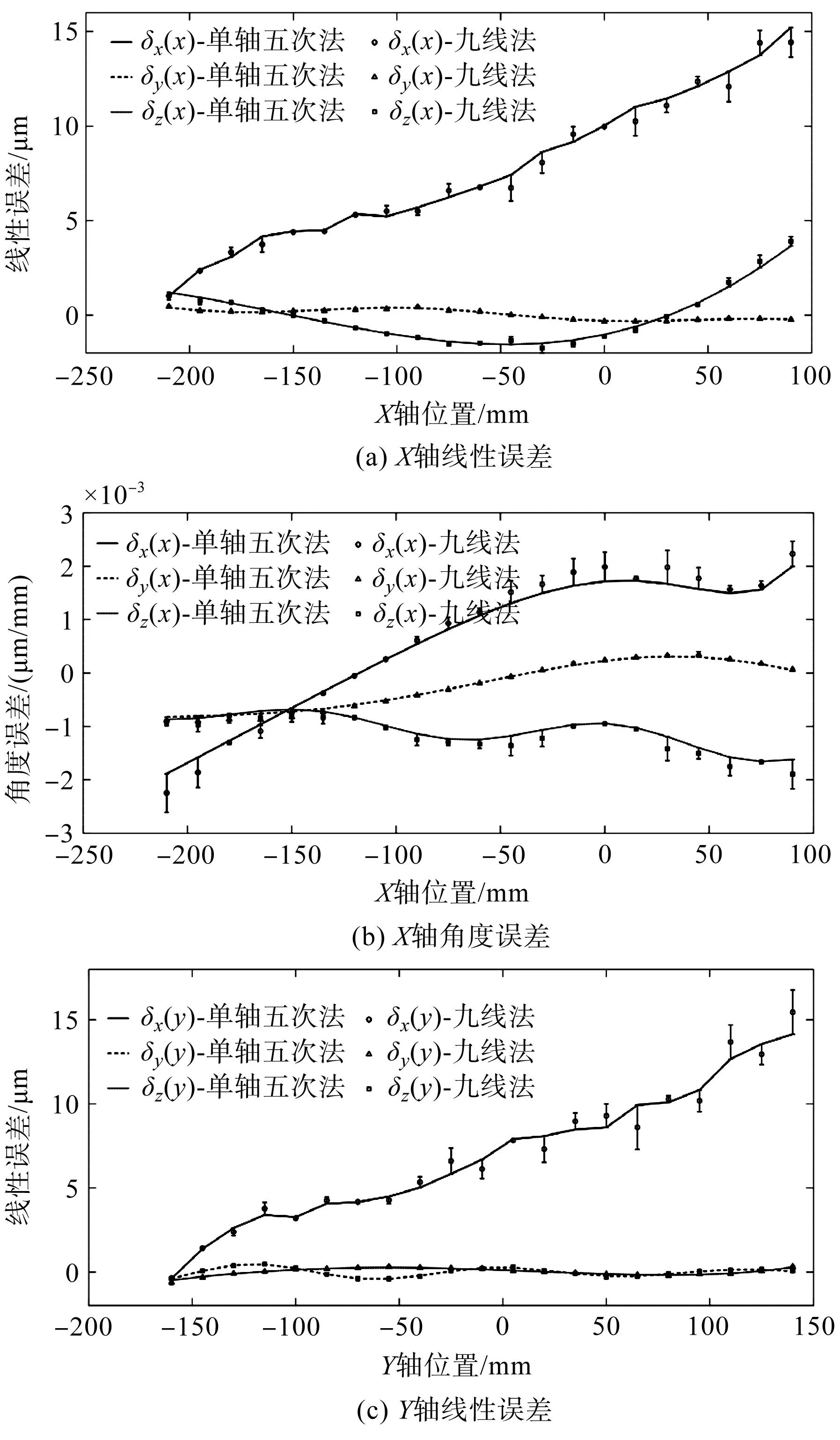
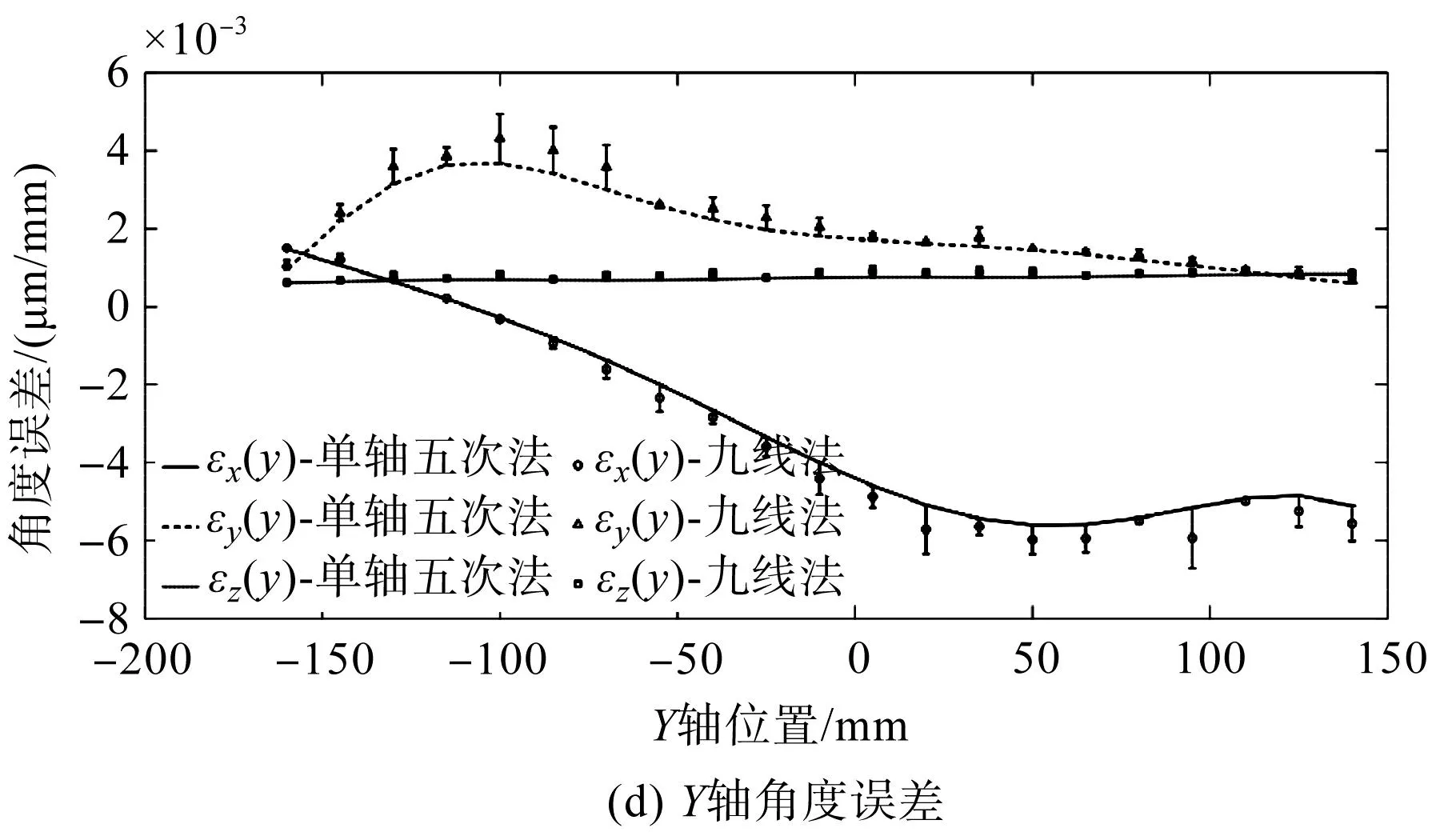
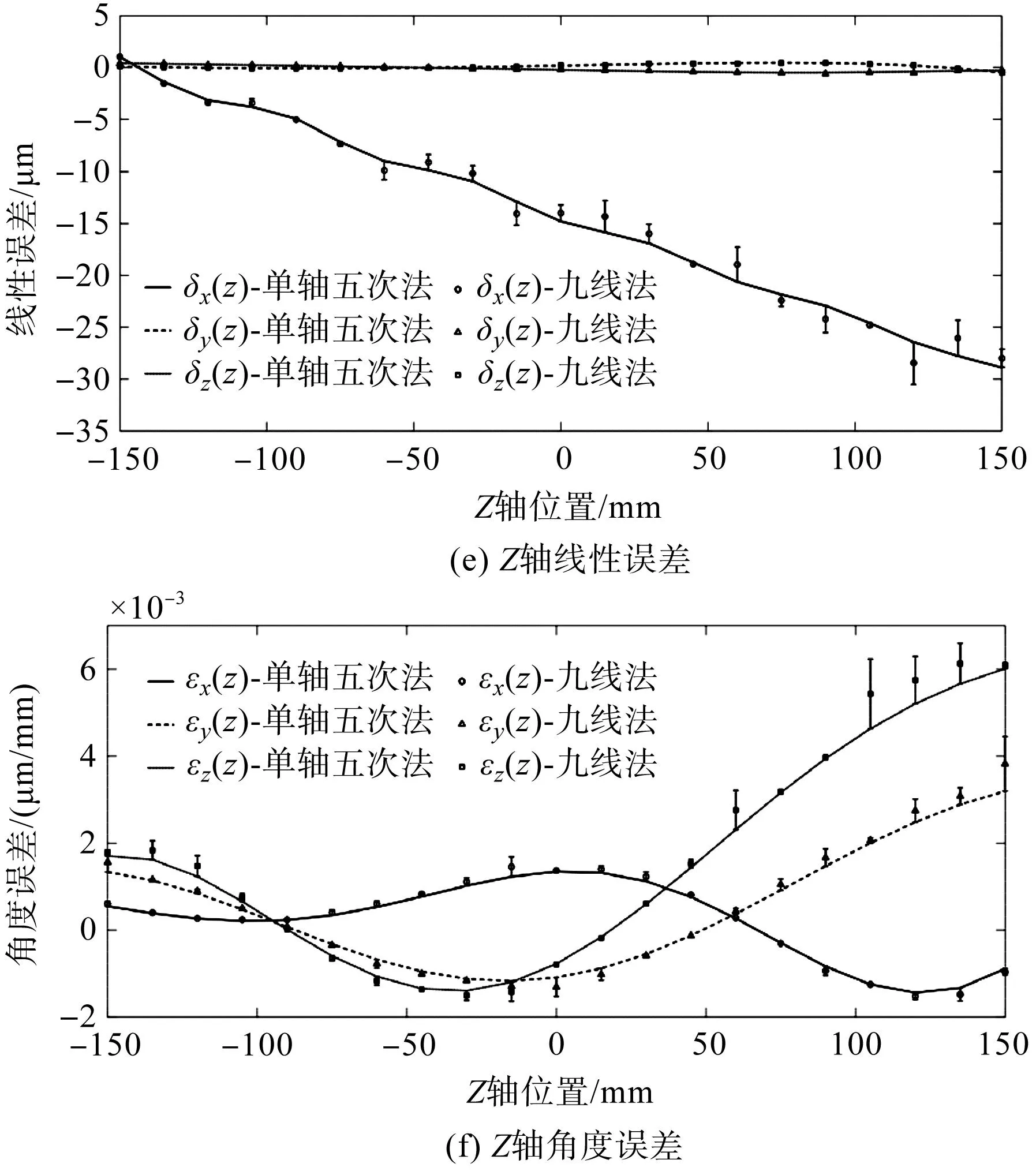
图12 单轴五次测量法与九线法对比Fig.12 Comparison between single-axis and five-times measurement method and nine-line method

由图12辨识结果可知:单轴五次测量法的辨识数据变化趋势与九线法辨识数据变化趋势基本一致,X、Y、Z轴线性误差辨识结果最大偏差分别为0.95 μm、1.31 μm、1.93 μm,角度误差辨识结果最大偏差分别为0.000 4 μm/mm、0.000 8 μm/mm、0.000 2 μm/mm,两种方法的垂直度误差辨识结果最大偏差为8.704 μm/m。几何误差测量结果一致性较好,辨识结果有效,验证了单轴五次测量法是准确的。

由此可见,针对每一项误差,可采用合适的参数化建模方法,得到X、Y、Z轴18项几何误差曲线,其他未测量位置点的误差数据可由模型曲线计算得出。

4 结束语

根据目前机床误差检测精度高、速度快等要求,笔者针对常用的基于激光干涉仪的机床空间几何误差多线测量辨识方法测量线数多、测量难度大、辨识精度低等情况,建立了一种新的机床空间几何误差测量辨识方法,即单轴五次测量法,并对该方法进行了实验验证。

主要研究结论如下:

1)根据机床直线轴实际运动状态,并结合激光干涉仪测量原理,提出了一种机床空间几何误差单轴五次测量方法,分析了激光干涉仪测量过程中的误差耦合情况,消除了传统多线法在求解过程中存在的误差传递现象,减少了测量线数与测量次数,采用单轴运动方式,有效避免了其他轴对当前运动轴误差的影响,提升了几何误差的测量辨识精度;

2)使用单轴五次测量法完成了机床空间几何误差的测量辨识实验,通过与空间九线法测量辨识结果的对比可知,两种方法测量辨识结果的空间误差向量最大偏差为1.93 μm,平均偏差为0.58 μm,验证了单轴五次测量法的准确性、有效性;

3)根据辨识的误差数据,结合误差综合模型以及单项误差参数化模型,可分析并绘制机床3个方向的综合误差分布场,为机床误差补偿及精度装配提供重要的理论依据与数据支持。

由于激光的测量波长会受到环境影响,诸如气压、气温以及湿度等,在测量过程中需引入仪器误差。因此,在后续的研究中,笔者将根据现场测量环境对仪器误差进行分析。