基于SORT映射的IRCMFDE在旋转机械故障诊断中的应用*

王潞红,邹平吉

(1.中国矿业大学 机电工程学院,江苏 徐州 221116;2.长治职业技术学院 机械电子工程系,山西 长治 046000;3.兰州职业技术学院 人事处,甘肃 兰州 730070)

0 引 言

随着计算机技术和智能算法的快速发展,机械设备健康监测和故障诊断方法也逐渐走向智能化和快速化。在旋转机械的故障监测中,机械振动信号在表征机器故障的敏感性方面要优于温度和压力等参数[1-2]。旋转机械的振源多种多样,在各种因素的耦合影响下,其振动信号呈现非线性和非平稳性,如何从中提取出有效的故障信息,并进行故障识别是研究的重点和热点之一[3]。

目前,基于熵的非线性动力学分析方法,如样本熵、模糊熵、排列熵、散布熵和波动散布熵等,因其具有强大的非线性数据分析性能,被广泛应用于旋转机械的健康监测和故障诊断领域[4]。杨云等人[5]利用排列熵提取了滚动轴承振动信号的损伤特征;但排列熵忽略了信号的幅值信息。葛红平等人[6]为了提高算法对信号幅值的敏感性,利用散布熵来表征滚动轴承的损伤状态;但散布熵未考虑信号的波动性。SHARMA S等人[7]将表征信号波动特性的波动散布熵用于旋转机械的故障诊断,取得了不错的识别结果;但波动散布熵只是从单一尺度描述信号的复杂性,分析不够全面。

为描述信号在不同尺度下的复杂性信息,AZAMI H等人[8]提出了多尺度波动散布熵(multiscale fluctuation dispersion entropy,MFDE),并用于生物时间序列的分析,取得了优于多尺度熵的分析效果;但在MFDE中,粗粒信号的长度与原信号长度和尺度因子的相关性较大,在尺度因子较大时,粗粒信号的长度会迅速减少,使得MFDE不可避免地遗漏部分关键故障信息[9-10]。

随后,为了提高MFDE的性能,钱恩丽等人[11]对MFDE的粗粒化构造方式进行了改进,提出了复合多尺度波动散布熵,用于单向阀的故障诊断;但该粗粒化方式依然遗漏了部分故障信息。姜万录等人[12]进一步提出了精细复合多尺度波动散布熵(refined composite multiscale fluctuation dispersion entropy,RCMFDE),并将其用于液压泵故障的精确表征;但基于均值的粗粒化序列构造方法存在较为复杂的平均计算,使得计算的效率较为低下,难以用于处理大批量的数据。徐哲熙等人[13]提出了时移多尺度波动散布熵,将其用于水电机组的故障诊断,准确地识别了故障类型;但时移粗粒化处理也面临着随着尺度的增加而误差增大的缺陷[14]。

在模式识别方面,相关向量机(relevant vector machine,RVM)在处理小样本的问题时优于支持向量机,具有更好的泛化性和稀疏性,但其核函数及其参数的选择对性能的影响较大,有必要对其参数进行优化设置[15]。朱兴统等人[16]采用蝙蝠算法(bat algorithm,BA)对RVM的参数进行了优化,构建了BA-RVM分类模型,实现了对滚动轴承故障进行精确识别的目的。

鉴于BA-RVM的优异分类性能,笔者引入BA-RVM作为故障分类器。

针对上述问题,笔者基于最小值的思想对RCMFDE的粗粒化方式进行改进,同时采用具有良好抗噪性能的SORT映射代替RCMFDE中的正态累积分布函数(normal cumulative distribution function,NCDF),提出一种基于SORT映射的改进精细复合多尺度波动散布熵(improved refined composite multiscale fluctuation dispersion entropy,IRCMFDE)和BA-RVM的旋转机械故障诊断方法。

首先,利用SORT映射代替传统RCMFDE中的NCDF映射,并利用最小值计算代替原始的平均值计算,生成基于SORT映射的IRCMFDE;随后,利用IRCMFDE提取旋转机械振动信号的故障特征,实现旋转机械的故障表征目的;最后,利用BA-RVM对旋转机械的故障类型进行智能识别,利用滚动轴承、齿轮箱和离心泵3种滚动轴承数据集对基于IRCMFDE和BA-RVM的故障诊断方法进行实验验证和分析。

1 改进精细复合多尺度波动散布熵

1.1 基于SORT映射的波动散布熵算法

常规波动散布熵采用的映射方式为正态分布函数(NCDF)。在杨采红等人[17]的研究中,基于SORT映射的散布熵取得了优于NCDF映射的效果。因此,笔者考虑将SORT映射引入至波动散布熵中,基于SORT映射的波动散布熵理论如下:

1)对于时间序列x={x1,…,xN},对其进行重构,得到时间序列y如下:

(1)

式中:L为y的长度;nc为类别数量;

2)对y进行排序,将排序结果置于向量sx中,同时排序索引置于向量osx中,定义标签向量cx,如下所示:

(2)

3)定义新向量z,其中元素zi的值为cx中与xi对应排序索引相同的元素,如下所示:

zi=cxj

(3)

式中:j为满足osxj=i的索引;

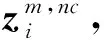
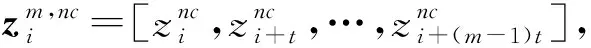
(4)

(5)

5)计算各潜在的散布模式πv0v1…vm-1的概率p(πv0v1…vm-1):

(6)

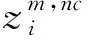
6)定义基于波动的散布熵为:

(7)

相比于常规的基于NCDF映射的波动散布熵,SORT映射由于没有复杂的计算,仅开展简单的重构和排序处理,因此具有较高的计算效率。

1.2 精细复合多尺度波动散布熵

MFDE的粗粒化处理截取的是非重叠片段,未全面考虑各片段两端邻近元素之间的相对关系,导致其熵值误差随着尺度因子的增加而逐渐变大,影响分析的可靠性[18]。因此,姜万录等人[19]提出了RCMFDE方法,优化了粗粒序列的构造模式。

RCMFDE的粗粒化是基于平均值来表征信号的特征信息,其具有稳定性好和性能优异的特点;但平均值作为描述信号一阶矩特征的方法,在计算过程中需要对片段中的两个以上元素进行平均,降低了分析效率。

1.3 改进精细复合多尺度波动散布熵

杨潇谊等人[20]1152-1153针对传统粗粒化的不足,利用精细复合粗粒化处理对时间序列进行多尺度分析,同时将粗粒化处理过程中的平均值计算替换为最大值计算,以表征数据隐含的信息量,用于准确快速地提取旋转机械振动信号中的故障信息。

笔者基于该思想对RCMFDE进行改进,并利用SORT映射代替NCDF映射,提高RCMFDE的特征提取性能和分析效率。

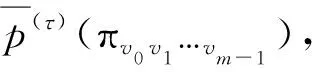
具体原理如下:

1)对于时间序列x={x1,…,xN},构造改进的粗粒化时间序列如下:

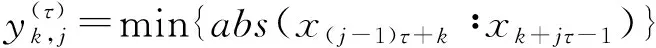
(8)

式中:abs()为绝对值函数;x(j-1)τ+k∶xk+jτ-1为数据点x(j-1)τ+k到数据点xk+jτ-1之间的全部数据点。

由式(8)可以发现:和RCMFDE中的基于平均值的粗粒化处理相比,基于最小值的粗粒化处理不需要进行多次求和,而是采用简单的排序处理即可以获得片段的最小值,因此,基于最小值的粗粒化处理的效率会高于基于均值的粗粒化处理的效率。

2)求解粗粒化序列的IRCMFDE,公式如下:

EIRCMFD(x,m,nc,t)=EFD(y(τ),m,nc,t)

(9)

2 旋转机械故障诊断模型

相关向量机是一种基于贝叶斯推理的稀疏概率网络,其将核函数作为基函数,而且其参数有着独立先验精度的优点,能够缓解支持向量机的不足。

然而RVM算法的性能与核函数参数的取值有关,为了提高算法的性能,笔者采用蝙蝠算法(BA)对其参数进行优化。BA是YANG Xin-she等人[21]提出的一种全局启发式优化算法,与遗传算法和粒子群优化算法相比,BA的效率和准确率都有明显提高,并且精度也有所提升。

为了增强旋转机械故障识别的精度和效率,笔者提出了一种基于SORT映射的IRCMFDE和BA-RVM[22]旋转机械故障诊断方法,其实现流程如图1所示。

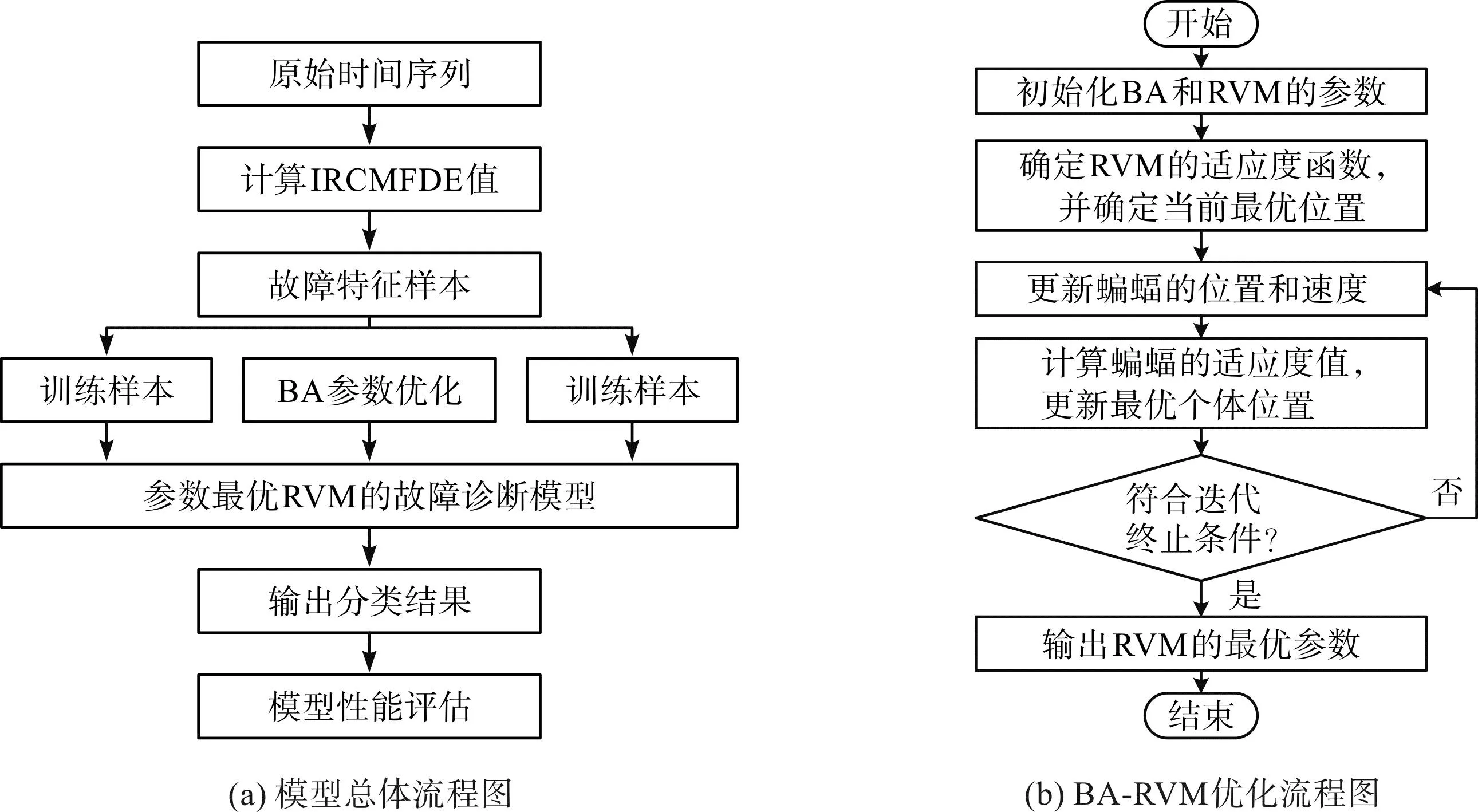
图1 基于IRCMFDE和BA-RVM的流程图Fig.1 Flowchart based on IRCMFDE and BA-RVM

基于IRCMFDE和BA-RVM的故障诊断方法的流程如下所示:

1)将旋转机械振动信号进行分割,得到多组M组长度为N的样本,其中随机抽取M1组样本作为训练样本,剩余M-M1组样本作为测试样本;

2)利用IRCMFDE提取样本的熵值特征,选取前20个尺度的特征,构造特征样本;

3)利用BA对RVM的参数进行优化,构造参数最优的RVM分类模型;

4)利用训练样本对BA-RVM分类模型进行训练,并通过测试样本对模型进行评估,得到旋转机械的故障识别结果。

3 故障诊断实验及分析

在进行实验时,需要预先设置IRCMFDE方法的4个参数,分别是数据长度N、嵌入维数m、类别数量nc和时间延迟t。

笔者采用了杨潇谊等人[20]1157的研究中的参数设置,即嵌入维数m=2,类别数量nc=3,时间延迟t=1,数据长度N=1 024,尺度因子τ=20。

3.1 滚动轴承实验

为验证基于IRCMFDE和BA-RVM旋转机械故障诊断方法的有效性,笔者利用滚动轴承数据集开展了实验研究。该圆柱滚子轴承数据集由Sant Longowal工程技术学院提供[23]。

实验平台如图2所示。

图2 滚动轴承实验平台Fig.2 Rolling bearing test platform

滚动轴承振动信号在2 050 r/min的转速下,采用三轴振动传感器(型号PCB3456A01),以70 kHz的频率进行信号收集,包含轴承座上垂直、水平和轴向3个方向的振动信号。

试验轴承是型号为NU205E的圆柱滚子轴承,笔者设置了3种状态类型:内圈故障、外圈故障、滚动体故障以及正常状态,如图3所示。

图3 圆柱滚动轴承的典型故障视图Fig.3 Typical fault view of cylindrical rolling bearings

对于该数据集,笔者采用无重叠的方式进行滑动采样;为了在一个周期内包含振动信号的完整信息,每1 024个数据点构造一个样本,每种故障样本都构造50个,其中30个样本是训练样本,其他20个样本是测试样本。

构造样本的信息如表1所示。

表1 滚动轴承试验样本信息Table 1 Rolling bearing test sample information

滚动轴承垂直方向振动信号的时域波形如图4所示。

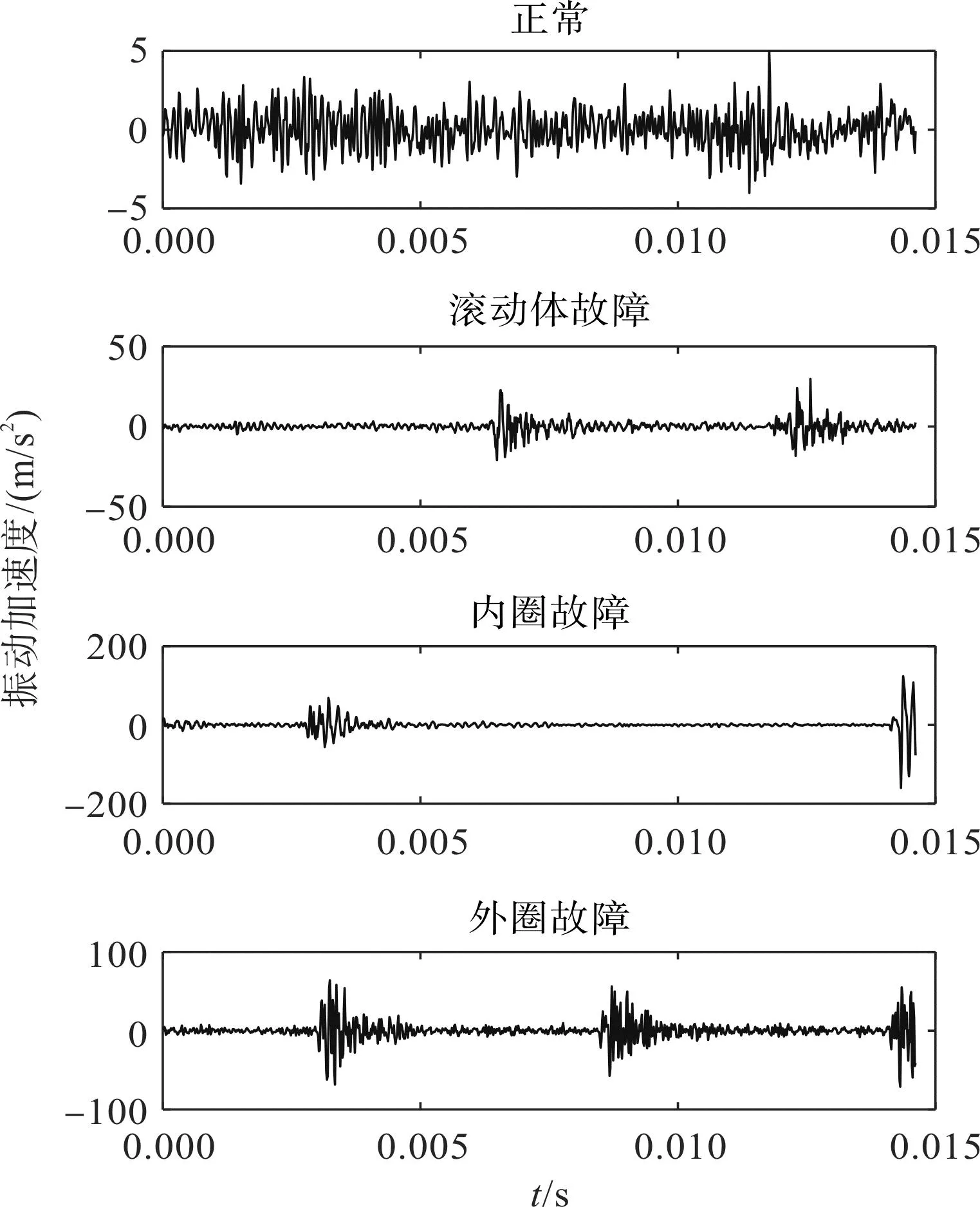
图4 滚动轴承垂直方向振动信号时域波形Fig.4 Time domain waveform of vertical vibration signal of rolling bearing

笔者利用IRCMFDE提取滚动轴承的故障特征,熵值曲线如图5所示。

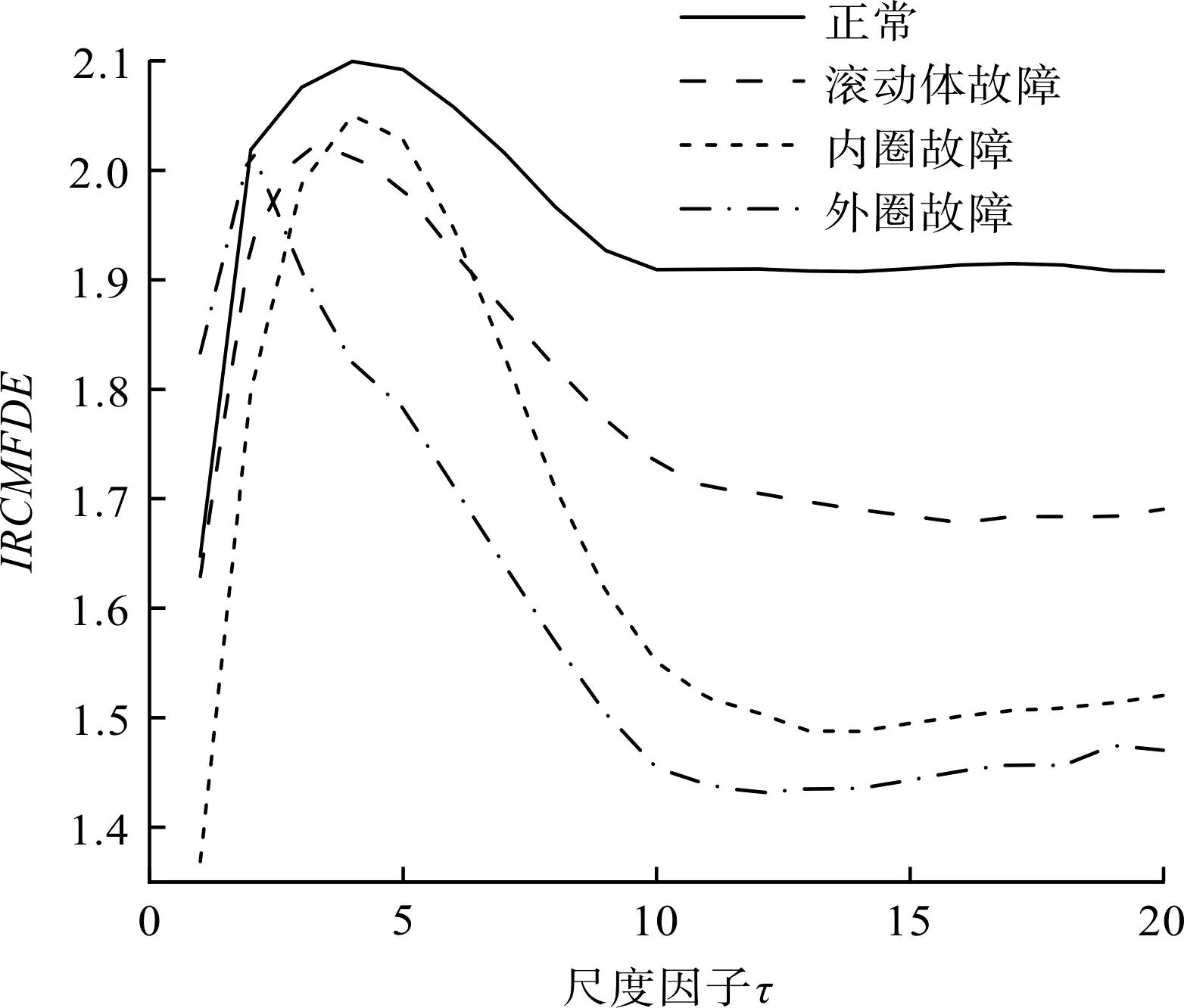
图5 滚动轴承不同工作状态下的IRCMFDEFig.5 IRCMFDE of rolling bearings under different working conditions

从图5可以发现:正常滚动轴承振动信号的IRCMFDE值大于相应故障样本的熵值,这是因为正常状态下的滚动轴承振动信号存在较多的随机冲击,规则性较弱、复杂性较强,因此IRCMFDE值最大。

另外,存在局部故障的滚动轴承振动信号中包含规律性的冲击成分,不规则性较低,因而熵值小于正常样本。

不同样本的熵值曲线具有比较明显的区分度,当尺度因子大于7后,各样本的熵值关系为正常>滚动体故障>内圈故障>外圈故障。这是因为实际运行中滚动轴承的不同位置出现损伤时,故障冲击造成的振动响应不同,因而振动信号具有不同的复杂性特征。

轴承外圈一般是固定的,当其出现局部损伤时,振动信号的周期性冲击成分非常显著,复杂性最低,IRCMFDE值最小。而轴承内圈一般与转轴一起旋转,损伤对振动信号的影响较小,其周期性较之外圈故障较弱,因此,内圈故障的IRCMFDE值大于外圈故障的IRCMFDE值。

类似地,轴承滚动体沿着转轴和自身进行旋转,与内外圈损伤相比,滚动体故障时,振动信号的损伤冲击响应非常弱,规则性较强[24]。

因此,图5中不同故障样本振动信号的IRCMFDE值符合理论和实际工况,证明IRCMFDE能够准确地分辨不同损伤类型,具有显著的物理意义。

在完成了全部样本的故障特征提取后,笔者使用BA-RVM进行了故障的识别。首先,将5种状态的150组训练样本输入至BA-RVM进行训练;随后,将剩余的5种状态的100组测试样本输入至训练完毕的BA-RVM模型中,进行模式识别。

最终的诊断结果如图6所示。

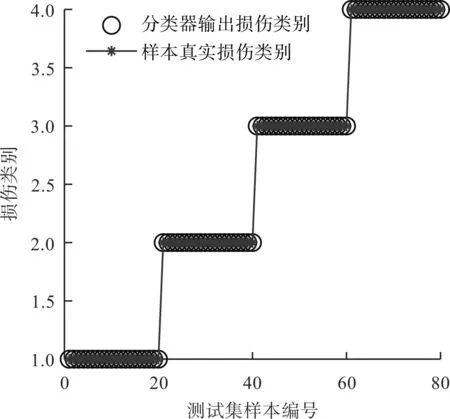
图6 基于IRCMFDE和BA-RVM方法的故障识别结果Fig.6 Fault identification results based on IRCMFDE and BA-RVM method

从图6可以发现:基于IRCMFDE和BA-RVM的诊断方法完成了对全部样本的准确识别工作,对滚动轴承的故障识别准确率达到了100%,证明了该方法的有效性。

随后,为进一步评估IRCMFDE方法的优越性,笔者对比了RCMFDE、精细复合多尺度样本熵(refined composite multiscale sample entropy,RCMSE)、精细复合多尺度模糊熵(refined composite multiscale fuzzy entropy,RCMFE)、精细复合多尺度排列熵(refined composite multiscale permutation entropy,RCMPE)和精细复合多尺度散布熵(refined composite multiscale dispersion entropy,RCMDE),将6种方法提取的20个尺度的故障特征输入至BA-RVM中进行故障识别,结果如表2所示。

表2 不同特征提取方法的故障识别结果Table 2 Fault identification results of different feature extraction methods

从表2可以发现:IRCMFDE方法在识别准确率达到了100%,同时,特征提取时间也仅为13.25 s,两种指标都优于其他5种方法,证明了该方法的优越性。

RCMFDE方法的特征提取时间多于IRCMFDE方法的原因在于IRCMFDE中基于最小值的粗粒化处理的计算复杂度低于RCMFDE中基于平均值的粗粒化处理复杂度,同时SORT函数的计算效率也较高。

因此,IRCMFDE方法不仅具有较高效率,而且能够准确地识别滚动轴承的故障类型。

为了进一步评估IRCMFDE方法的稳定性和优越性,笔者将上述6种方法提取的故障特征输入至BA-RVM分类器中,进行10次重复分类,统计对应的平均分类准确率。

详细的识别结果如表3所示。

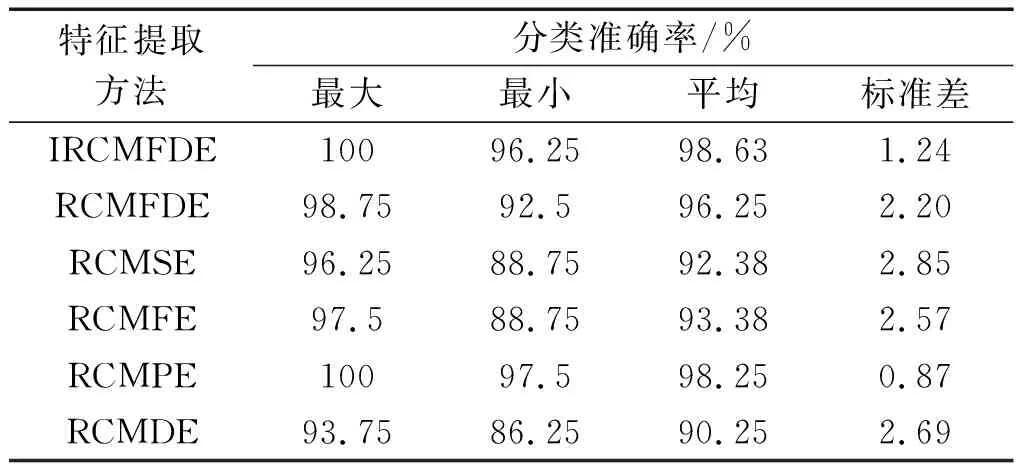
表3 不同特征提取方法的详细分类结果Table 3 Detailed classification results of different feature extraction methods

由表3可知:IRCMFDE方法的平均分类准确率最高,达到了98.63%,而RCMPE方法次之,为98.25%,证明这2种方法都能够准确可靠地识别滚动轴承的故障类型。

但RCMPE方法的标准差小于IRCMFDE方法,证明RCMPE方法的稳定性更优,然而根据表2中的结果,RCMPE方法的效率非常低,特征提取所需要的时间超过IRCMFDE方法的10倍以上。

因此,IRCMFDE方法在特征提取效率和分类性能方面优于其他5种方法。

为了证明基于SORT映射的IRCMFDE的噪声鲁棒性,笔者在振动信号中加入不同信噪比的白噪声,以模拟实际工业环境下强噪声的影响,结果如表4所示。

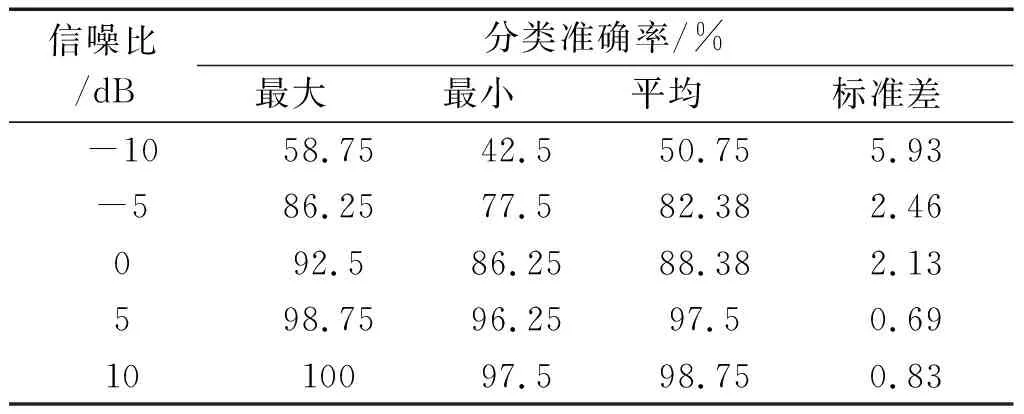
表4 不同信噪比下IRCMFDE方法的分类结果Table 4 Classification results of the IRCMFDE method under different signal-to-noise ratio

由表4可以发现:当信噪比为-10 dB时,IRCMFDE方法的平均分类准确率仅为50.75%;随着信噪比的增加,准确率也显著增加,当信噪比为0 dB时,平均准确率已经能够达到88.38%;而当信噪比提高到5 dB时,IRCMFDE方法的平均准确率也增加至97.5%。

由此可见,当振动信号的信噪比高于0 dB时,该方法能够取得较为可靠的故障识别结果,具有一定的抗噪性。

3.2 齿轮箱实验

随后,为了进一步验证基于IRCMFDE和BA-RVM方法的有效性,笔者利用齿轮箱故障数据集进行实验分析[26]。

该齿轮箱数据集来自于QPZZ-II实验平台所采集的输出轴振动信号。该平台的主要组成包含驱动电机、轴承、齿轮箱和磁粉制动器。

平台具体结构和传感器的布置方式如图7所示。

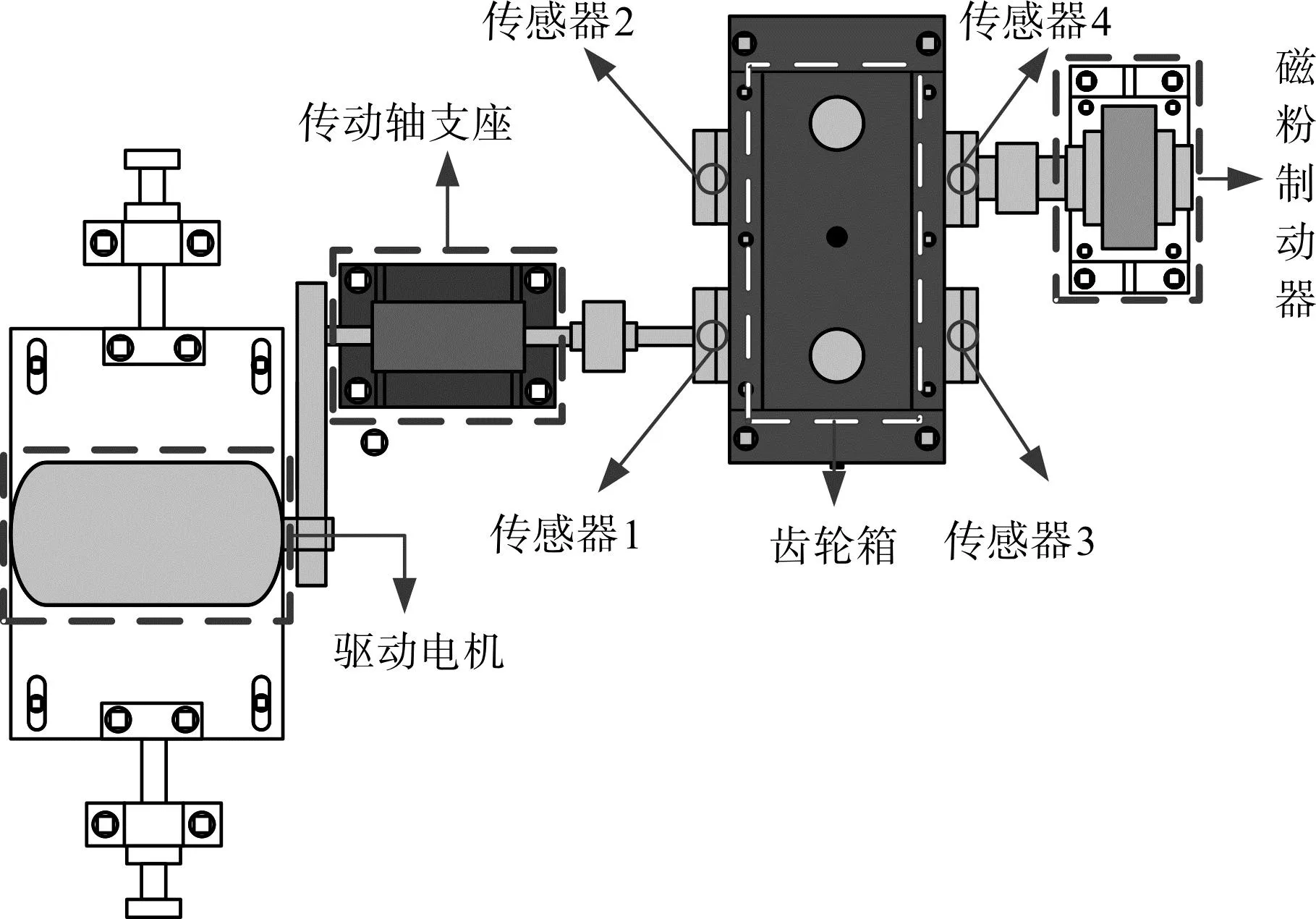
图7 QPZZ-II实验平台的结构和传感器的布置方式 Fig.7 The structure of the QPZZ-II experimental platform and the arrangement of sensors

每种工况样本的数据点数为1 024,笔者构造了互不重叠的50组样本,每种工况和实验过程中的详细参数信息如表5所示。

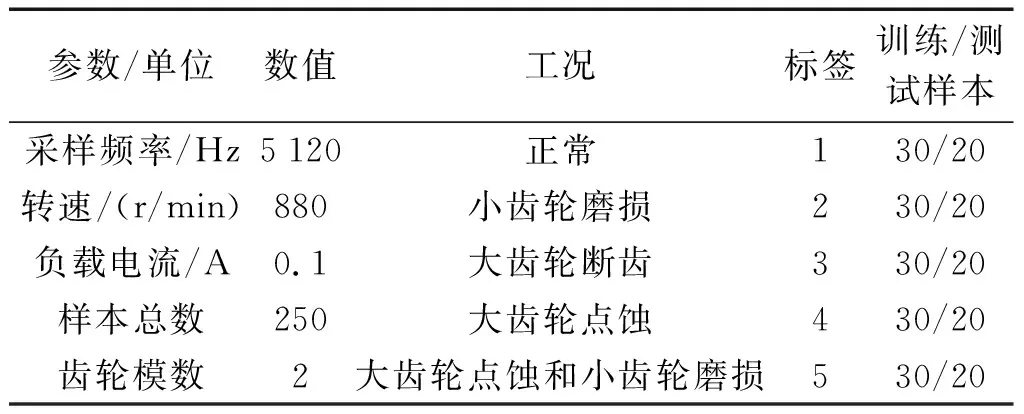
表5 实验的不同工况和具体参数的详细信息Table 5 Details of different conditions and specific parameters of the experiment

齿轮箱振动信号的时域波形如图8所示。

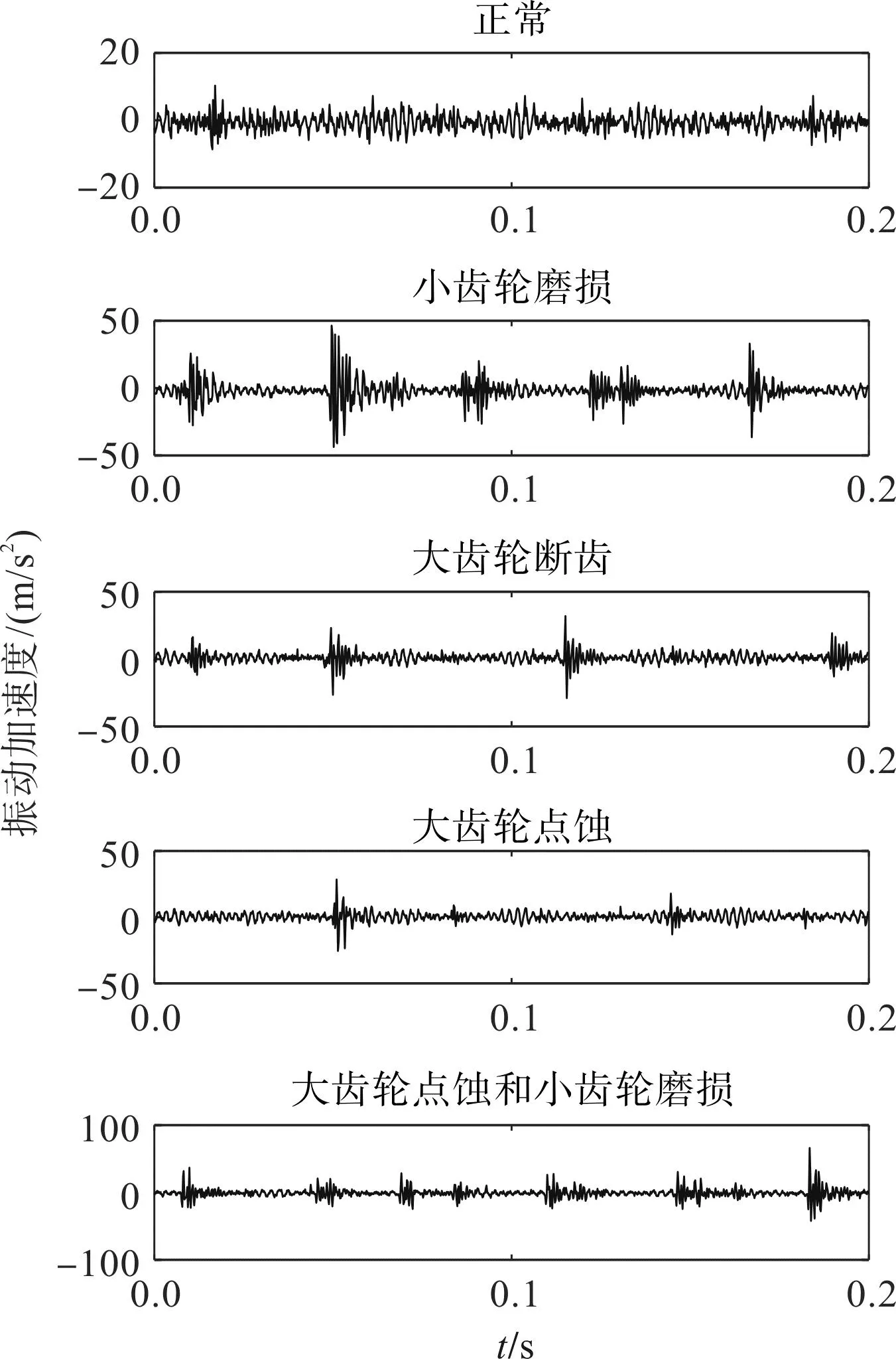
图8 齿轮箱振动信号的时域波形Fig.8 Time domain waveform of gearbox vibration signal

笔者利用IRCMFDE提取振动信号的故障特征,熵值曲线如图9所示。

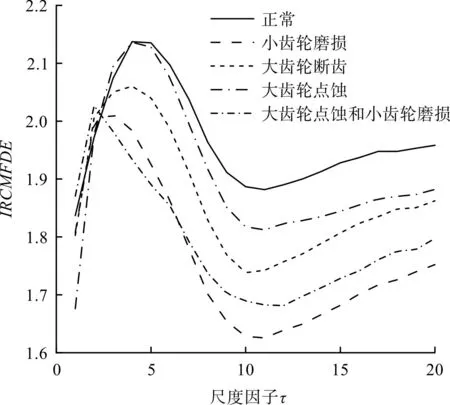
图9 齿轮箱不同工作状态下的IRCMFDEFig.9 IRCMFDE of gearbox under different working conditions

由图9可知:在大多数尺度上,正常齿轮箱振动信号的IRCMFDE值大于相应故障样本的熵值,这表明正常齿轮箱振动信号的复杂性大于相应包含周期性冲击的故障齿轮箱振动信号的复杂性,而且IRCMFDE方法能够精准地区分不同状态齿轮箱振动信号之间的复杂性差异。当尺度因子大于8后,5种状态齿轮箱的熵值曲线具有非常明显的差异。

以上结果证明,IRCMFDE方法可以有效地区分不同样本的故障类型,同时该方法可以通过设定检测阈值,来检测齿轮箱是否存在故障。

随后,笔者将样本的故障特征输入至BA-RVM分类器进行故障识别,诊断结果如图10所示。

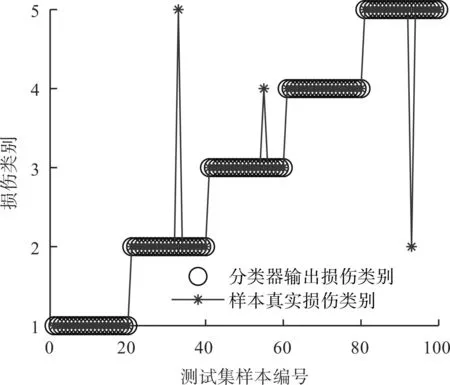
图10 基于IRCMFDE和BA-RVM方法的故障识别结果Fig.10 Fault identification results based on IRCMFDE and BA-RVM method

根据图10可以发现:基于IRCMFDE和BA-RVM的方法错误地识别了3个样本:分别将1个小齿轮磨损样本错误地识别为复合故障(大齿轮点蚀和小齿轮磨损)样本,1个大齿轮断齿样本错误识别为大齿轮点蚀样本,1个复合故障样本错误识别为小齿轮磨损样本。

该方法故障识别准确率为97%,证明该方法在齿轮箱的故障识别方面具有一定的有效性。

随后,为进一步评估IRCMFDE方法的优越性,笔者对比了IRCMFDE、RCMFDE、RCMSE、RCMFE、RCMPE和RCMDE,将6种方法提取的20个尺度的故障特征输入至BA-RVM中,进行故障识别,结果如表6所示。

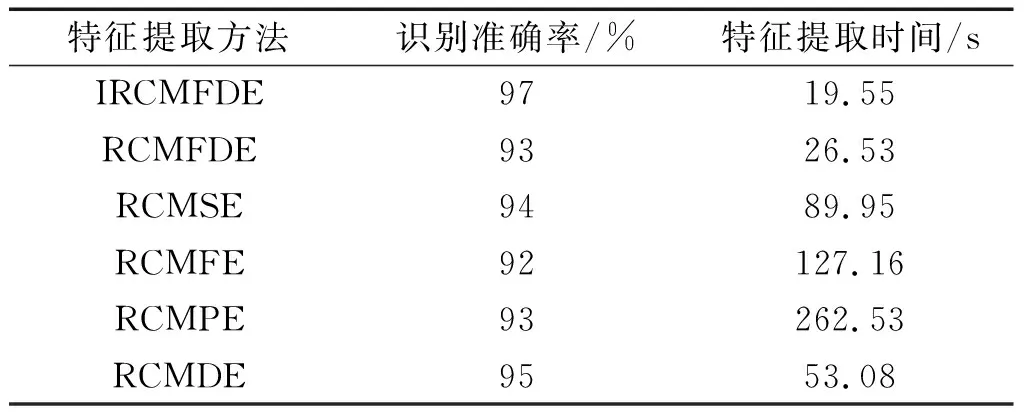
表6 不同特征提取方法的故障识别结果Table 6 Fault identification results of different feature extraction methods

由表6可知:基于IRCMFDE的故障诊断方法取得了最高的识别准确率,且具有最高的特征提取效率,为19.55 s;其在准确率和效率方面都要优于其他5种方法,再一次证明了该方法的优越性。

为了进一步评估IRCMFDE方法的稳定性和优越性,笔者将上述6种方法提取的故障特征输入至BA-RVM分类器中,进行10次重复分类,统计对应的平均分类准确率,详细的识别结果如表7所示。

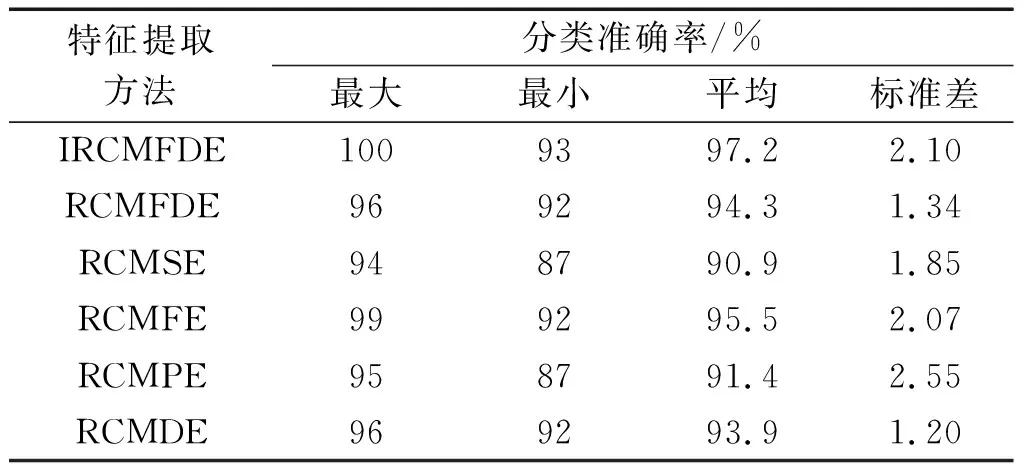
表7 不同特征提取方法的详细分类结果Table 7 Detailed classification results of different feature extraction methods

由表7可知:基于IRCMFDE和BA-RVM的方法的平均分类准确率最高,为97.2%,证明了其在处理分类识别问题时是可靠的。

基于IRCMFDE和BA-RVM的方法在最大分类准确率、最小分类准确率和平均分类准确率方面均优于其他5种方法,证明了该方法的优越性。但是该方法的标准差仅优于RCMPE方法的标准差,证明该方法的分类结果不太稳定,容易出现波动,但总的来说该方法具有一定的可靠性。

同样地,为了证明基于IRCMFDE和BA-RVM方法的抗噪性,笔者在振动信号中添加不同信噪比的噪声,再进行故障特征的提取。不同信噪比下基于IRCMFDE和BA-RVM方法的诊断结果如表8所示。

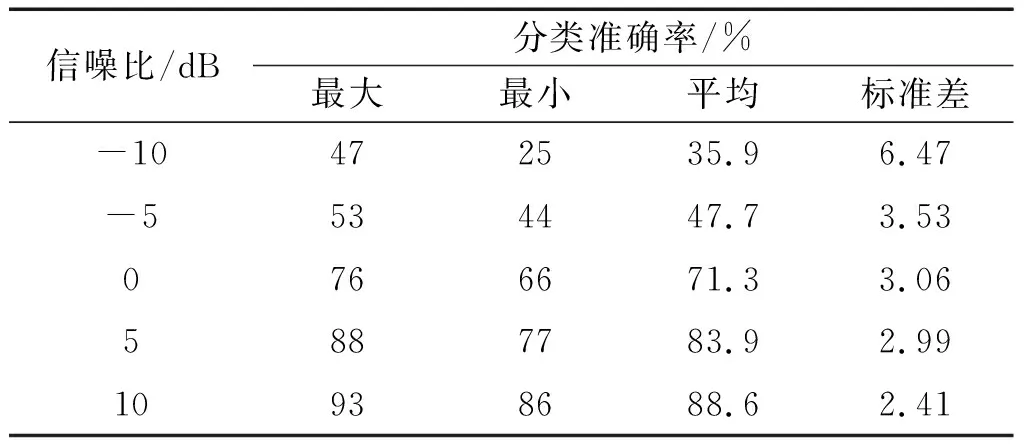
表8 基于IRCMFDE和BA-RVM方法的分类结果Table 8 Classification results based on IRCMFDE and BA-RVM method

由表8可以发现:随着信噪比的增加,基于IRCMFDE和BA-RVM方法的最大准确率、最小准确率和平均准确率都随之增加,而标准差则随之减小,这证明信噪比的提高有助于提高诊断准确率。

当信噪比达到5 dB时,该方法的平均识别准确率能够达到80%以上,具有一定的抗噪性。

3.3 离心泵实验

最后,为了检验基于IRCMFDE和BA-RVM方法的通用性,笔者利用离心泵故障数据集进行实验。实验平台如图11所示[27]。

图11 离心泵实验平台Fig.11 Centrifugal pump test platform

实验中,笔者利用振动加速度计(型号为PCB353B34)和麦克风采集了离心泵的叶片和轴承在受到不同损伤时的振动信号和声信号,进行了后续分析。

每种工况样本的数据点数为1 024,笔者构造了互不重叠的50组样本,实验过程中的详细参数信息如表9所示。

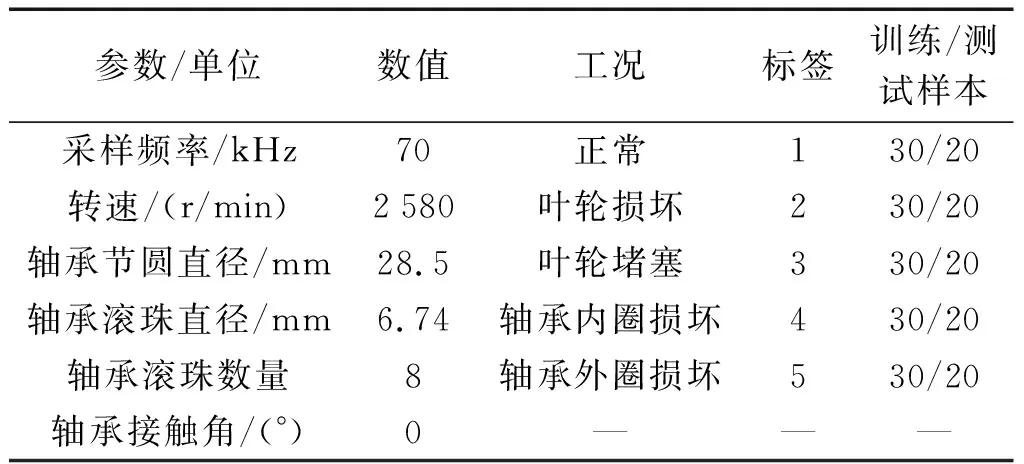
表9 实验的不同工况和具体参数详细信息Table 9 Details of different conditions and specific parameters of the experiment

离心泵振动信号的时域波形如图12所示。

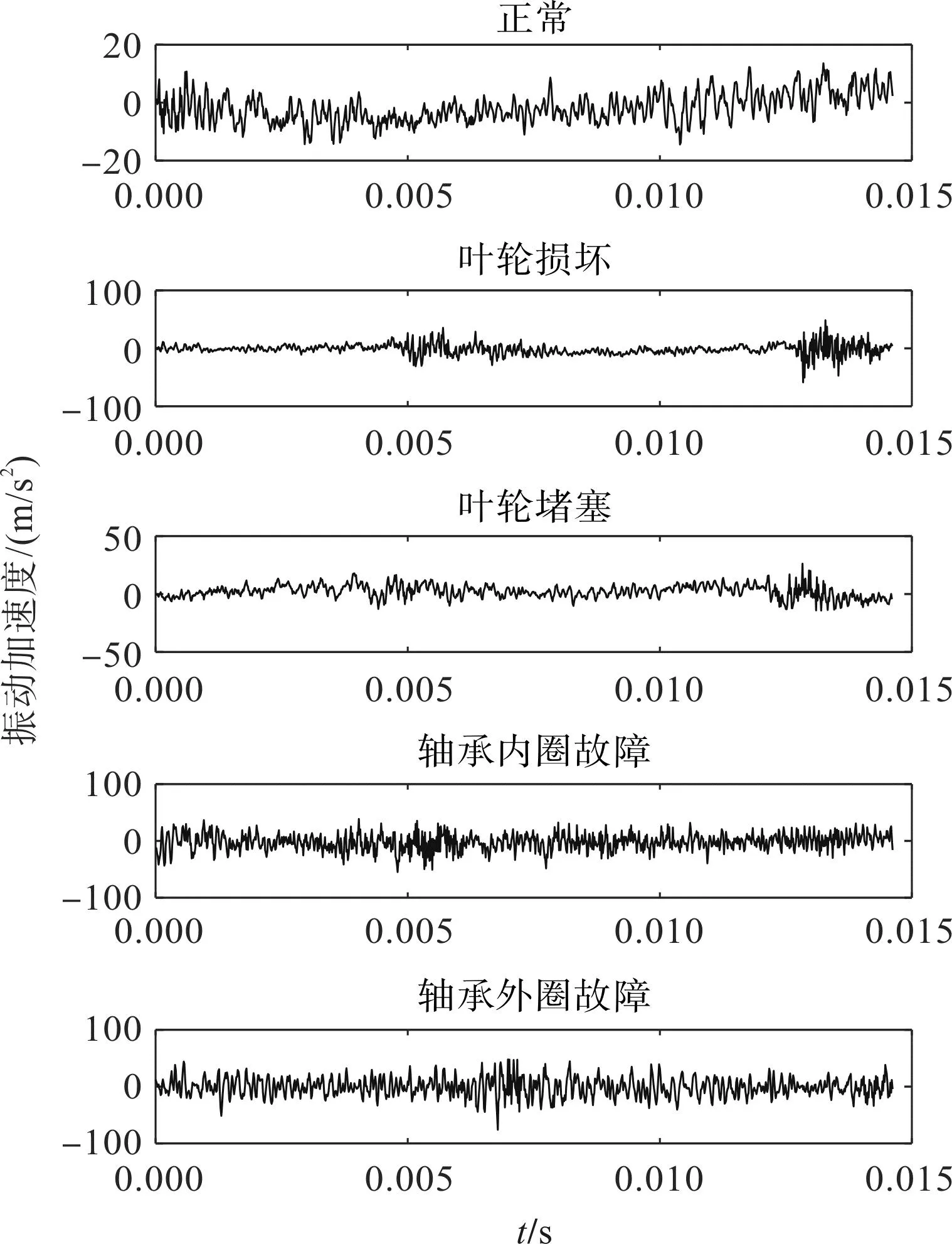
图12 离心泵振动信号的时域波形Fig.12 Time domain waveform of centrifugal pump vibration signal

笔者利用IRCMFDE提取振动信号的故障特征,熵值曲线如图13所示。

由图13可以发现:在大多数尺度因子上,正常离心泵振动信号的IRCMFDE值小于其他故障样本的熵值,且不同状态样本之间具有很大的区分度,证明IRCMFDE能够有效地提取样本信号之间的复杂度差异,并进行准确区分。

而正常样本的复杂度小于其他样本的复杂度,这表明可以通过设定一个阈值,当样本的熵值小于该阈值时,证明该样本为健康样本;而当熵值大于该阈值时,证明样本存在故障。

这充分验证了IRCMFDE在测量信号复杂度方面的有效性。

随后,笔者将通过上述6种特征提取方法构造的故障特征输入至BA-RVM中,进行故障识别,结果如表10所示。

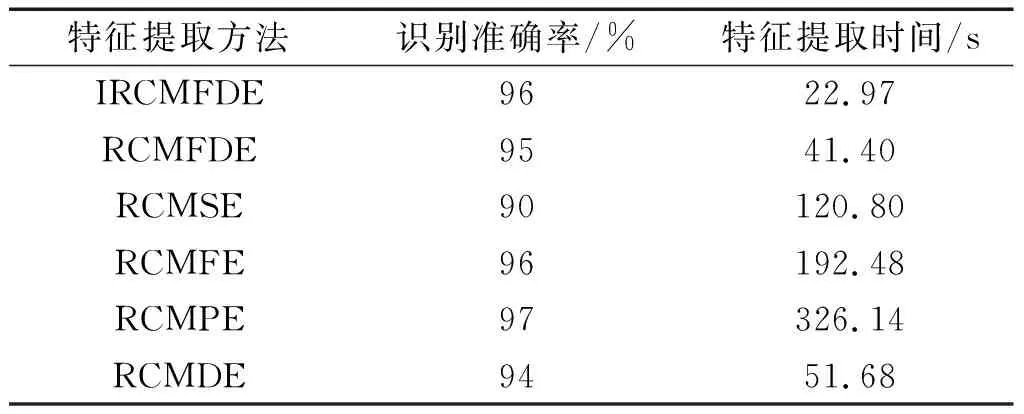
表10 不同特征提取方法的故障识别结果Table 10 Fault identification results of different feature extraction methods

由表10可知:IRCMFDE方法的准确率低于RCMPE方法的准确率,与RCMFE方法相同;但该方法的效率是最高的,只需要22.97 s即可完成故障特征的提取,证明了该方法的优越性。

随后,笔者同样进行了多次实验,以评估IRCMFDE方法的优越性和稳定性,结果如表11所示。

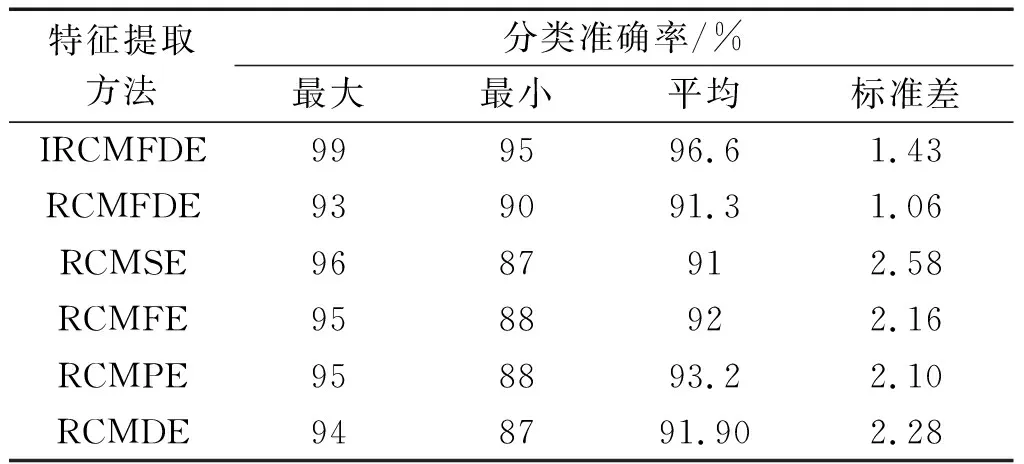
表11 不同特征提取方法的详细分类结果Table 11 Detailed classification results of different feature extraction methods

从表11可以发现:在平均准确率方面,IRCMFDE方法最高,为96.6%;最大准确率方面,IRCMFDE方法最高,为99%;最小准确率方面,IRCMFDE方法最高,为95%;在标准差方面,RCMFDE方法最低,为1.06,而IRCMFDE方法次之,为1.43。

上述结果证明,基于IRCMFDE和BA-RVM方法的性能最优,其能够完成对离心泵的准确诊断工作。

最后,笔者对基于IRCMFDE和BA-RVM方法的抗噪性进行研究,结果如表12所示。

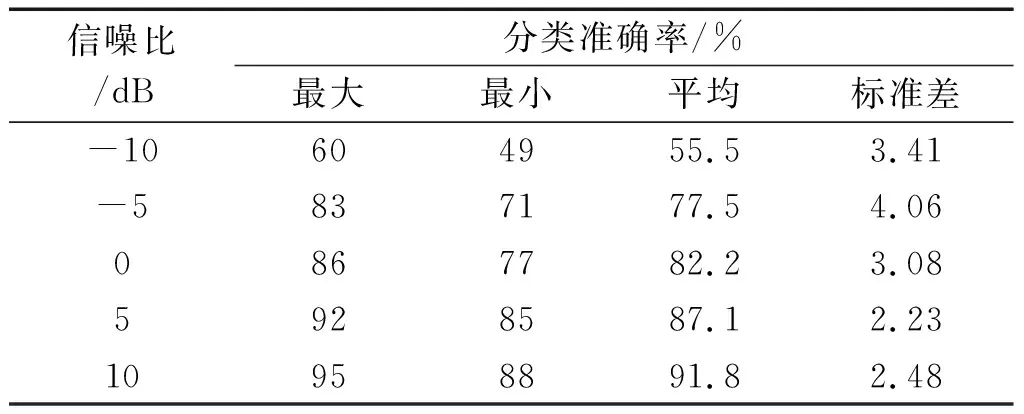
表12 不同信噪比下基于IRCMFDE和BA-RVM方法的分类结果Table 12 Classification results based on IRCMFDE and BA-RVM method under different signal-to-noise ratio

由表12可以发现:基于IRCMFDE和BA-RVM方法的平均准确率在信噪比为0 dB时能够达到82.2%;而信噪比为10 dB时,平均准确率能够达到91.8%,说明该方法具有较好的噪声鲁棒性,适用于实际工业的故障诊断问题。

4 结束语

针对旋转机械的故障识别准确率不佳和特征提取效率较低的问题,笔者提出了一种基于SORT映射的IRCMFDE和BA-RVM的旋转机械故障诊断方法,利用滚动轴承、齿轮箱和离心泵3种典型的旋转机械数据集,对该方法开展了实验分析,验证了该方法的有效性。

研究结论如下:

1)SORT映射和改进的粗粒化处理提高了RCMFDE方法的特征提取效率和性能,IRCMFDE相较于RCMFDE、RCMSE、RCMFE、RCMPE和RCMDE,在特征表征准确度和效率方面更优,识别精度较为稳定;

2)基于IRCMFDE和BA-RVM的旋转机械故障诊断方法在识别滚动轴承、齿轮箱和离心泵的故障时,分别取得了100%、97%和96%的识别准确率,平均准确率分别为98.63%、97.2%和96.6%,同时特征提取时间分别为13.25 s、19.55 s和22.97 s,该方法具有较为优异的性能。

采用该方法得到的诊断准确率虽然很高,但是仍然存在不足,证明振动信号中存在较多的干扰。在后续的工作中,笔者将对振动信号进行去噪处理,以提高该方法的故障诊断准确率。