ANPC 三电平换流器高效电磁暂态建模仿真方法

李 漾，田 芳，张 星，穆 清

（电网安全与节能国家重点实验室（中国电力科学研究院有限公司），北京 100192）

0 引言

新能源领域换流器应用场景的功率和电压不断增加，三电平换流器较传统两电平换流器具有电力电子开关器件承压小、容量大、输出电能质量高等优势，满足了高效化和经济化需求［1］。在三电平换流器典型的几类拓扑结构中，ANPC（有源中性点钳位型）拓扑缓解了传统NPC（中性点钳位型）拓扑开关管损耗不均的情况，延长了变流器的使用寿命［2］，近年来被广泛地应用于中高压大功率场景下风电、光伏出口的主电路设计中。在此背景下，ANPC 三电平换流器仿真建模领域的相关研究工作需求也在增大。

国内外关于电力系统电磁暂态模型展开了大量研究，从器件级、变换器级、系统级尺度提出了不同复杂程度的建模方法［3］，目前用于电磁暂态仿真分析的换流器建模方法主要有基于外特性建模的开关函数模型和平均值模型，以及基于开关器件级建模的开关详细模型［4］。针对不同的研究目的和仿真场景，建模要求也不尽相同［5］。目前各仿真平台大都通过组合现有的元件库基本元件（如IGBT（绝缘栅双极型晶体管）、二极管、电容器等）来构建ANPC换流器模型，暂无ANPC三电平换流器专有仿真模型设计，因此需要提出适用于较大规模小步长实时仿真场景，兼顾计算精度与效率的电磁暂态仿真模型。

ANPC 三电平换流器建模仿真研究通常都是基于大规模区域级电网实时仿真应用场景，且需要采用比常规电磁暂态仿真步长（50 μs）更小的仿真步长（2 μs）实现高频电力电子开关精确仿真。为满足仿真规模和精度的要求，电力电子系统的实时仿真往往需要结合特定的硬件平台实现。现有仿真平台如ADPSS（电力系统全数字实时仿真装置）采用异构计算平台和并行计算架构高效算法［6］，通过FPGA（场效应可编程逻辑阵列）实现电力电子设备的小步长实时仿真，并与基于CPU（中央处理器）实现的常规大步长仿真联合完成仿真任务。但目前基于该架构的实时仿真装置仍面临许多技术需求与挑战：一方面，平台中电力电子装置专有模型库资源较为匮乏，新拓扑结构的电力电子装置专有化建模研究无法满足现有仿真分析需求；另一方面，基于FPGA 的小步长仿真平台硬件资源约束使得电网仿真节点受限，难以进一步扩大规模。

现有的关于ANPC 三电平换流器的电磁暂态建模方法映射到基于FPGA 的小步长实时仿真应用场景中时，均存在模型详细程度或实时性方面的不足，难以兼顾仿真精度和效率，同时面临FPGA 有限硬件资源导致的仿真规模瓶颈问题。ANPC 三电平换流器目前尚没有针对小步长实时仿真场景下兼顾精度和效率、节约计算资源的专有化电磁暂态建模方法。

针对ANPC 三电平换流器在电磁暂态仿真研究领域的不足，本文提出一种适用于小步长实时仿真的ANPC 三电平换流器高效电磁暂态仿真模型。该建模方法能反映设备内电气特性，具有较高的仿真精度，相比基于电力电子开关建模的详细变流器模型有明显的速度提升。模型通过构造ANPC 三电平换流器的离散化伴随电路，基于Ward等值方法消去内部节点，得到桥臂多端口诺顿等效电路。最后，在MATLAB/Simulink 平台中对基于该等效模型搭建的仿真系统进行仿真精度验证和仿真速度测试。该降阶等效模型在电磁暂态算法求解流程中计算复杂度明显降低，且实现了节点降维，可实现小步长仿真电网规模的扩大。

1 ANPC三电平换流器

1.1 电路拓扑和工作原理

ANPC 三电平拓扑结构如图1 所示，其中：n为电压中性点；T1—T6为IGBT 管；D1—D6为反并联二极管；C1和C2为直流稳压电容；UDC为直流侧电压。该拓扑由经典的NPC 拓扑改进得到，用IGBT-二极管并联开关组替代了中性点电压钳位的两个二极管，相对于中性点能输出三种确定的电平。一方面，三电平拓扑结构与传统的两电平相比较，输出谐波含量更低，电压利用率更高，开关承压更小，更适用于较大功率新能源出口场景；另一方面，ANPC 相较于NPC 拓扑，通过采用主动开关增加了零电平输出下的换流回路开关状态组合，通过控制对冗余零电平的切换，在一定程度上实现了开关管的损耗平衡，有效弥补了NPC 拓扑因复杂的长换流路径导致的开关器件组内外管损耗不均的缺点。常用的ANPC 拓扑有常规型结构和混合型结构［7］，两种拓扑的结构和工作原理基本相同，区别在于常规型拓扑所有开关组均采用同类型IGBT，而混合型拓扑中内开关管用SiC MOSFET（碳化硅金属氧化物半导体场效应晶体管）替代。本文对适用于大功率变流器模块设计的常规型ANPC拓扑进行研究分析。

图1 ANPC三电平拓扑结构Fig.1 Topology of an ANPC three-level converter

不考虑控制方法，仅从输出的三种电平有效换流回路进行分析，ANPC 三电平桥臂开关状态如表1所示。ANPC三电平拓扑理论上输出为零电平的状态一共有4种，提供了多种换流回路的开关状态组合。

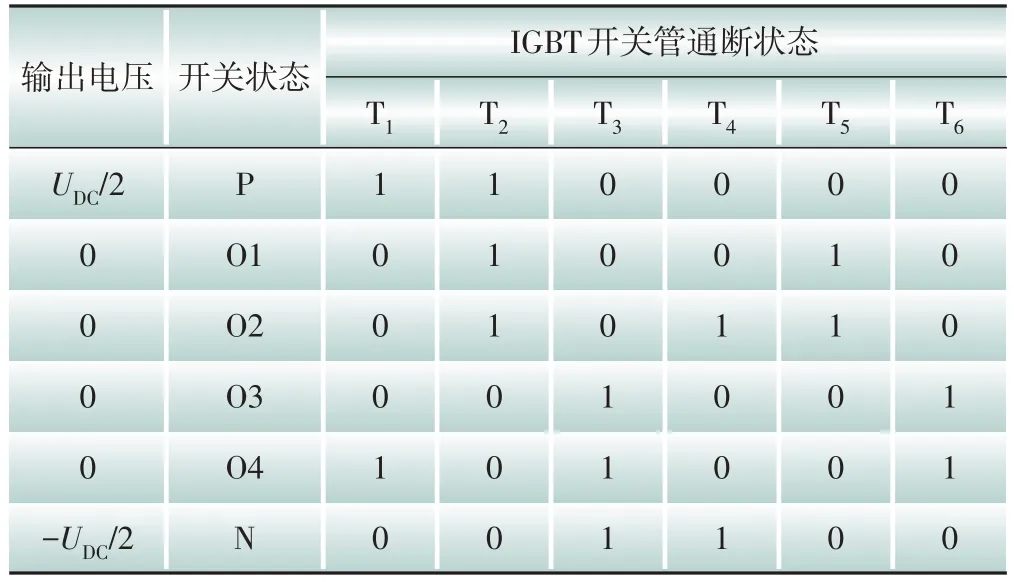
表1 ANPC三电平桥臂开关状态Table 1 Switching states of an ANPC three-level bridge arm

ANPC三电平换流器系统模型如图2所示，其中：LF为滤波电感；CF为滤波电容；LS为交流网侧等效电感；US为交流网侧电压源。除了变流器主拓扑，变流器交流侧一般包括滤波电路、变压器、交流电压源。三电平换流器中，PWM（脉宽调制）是最常用的调制策略，一般采用SPWM（正弦脉宽调制）［8］，如图3 所示，调制波与双向载波比较即得到各开关管触发信号。

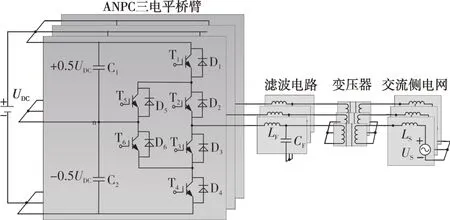
图2 ANPC三电平换流器系统模型Fig.2 The model of ANPC three-level converter

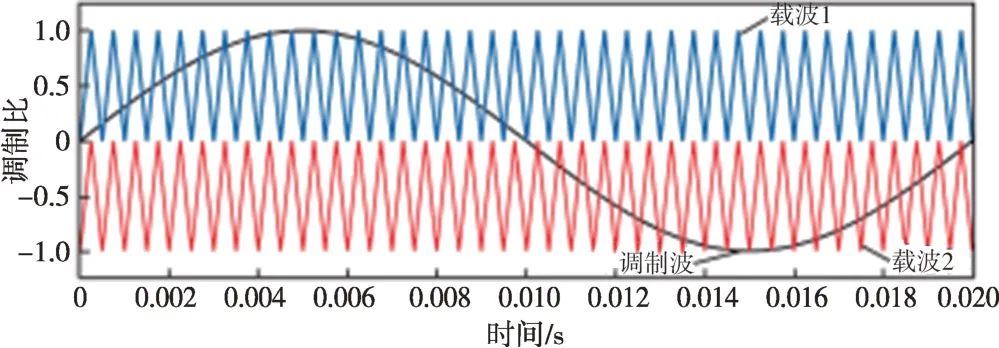
图3 三电平换流器SPWM调制Fig.3 SPWM modulation of a three-level converter

开关管T2和T3为互斥通断的工频开关管，其开通和关断由调制波的正负决定。将上层载波信号与调制波进行比较，得到互斥的开关管T1和T5动作信号，此时T2常开，三电平换流器交替输出为1电平或0电平；下层载波信号与调制波进行比较，得到互斥的开关管T4和T6动作信号，此时T3常开，三电平换流器交替输出为0电平或-1电平。由此可以得到ANPC 三电平拓扑的各个开关管触发信号如图4所示。

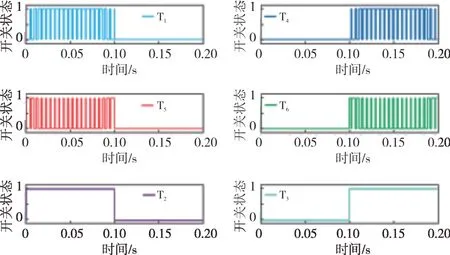
图4 ANPC三电平开关触发信号Fig.4 Trigger signals of an ANPC three-level switch

1.2 电力电子电磁暂态建模方法

在电力系统电磁暂态仿真研究中，研究目的和应用场景不同，对电力电子设备模型的精度和仿真速度要求也不同。电力电子装置基本的建模方法大致可分为外特性建模法和开关器件级建模法［9］。

外特性建模法根据装置整体输入输出特性进行等效建模，可以有效地描述设备电气特性和响应，实现装置对外部电路的等效。基于外特性建模的主要模型通常有平均值模型和开关函数模型。文献［10］介绍了一种模块化多电平换流器桥臂全状态平均值仿真模型，以电气变量在开关周期内的平均值代替其实际值的方式进行简化，但模型无法模拟设备的高频电磁暂态现象。开关函数模型则引入开关通断对应取值的开关函数，根据表达式描述设备开关特性来实现建模［11-12］，该模型中开关不具有实际物理意义，不能用于内特性分析。

开关器件级建模法以电力电子开关元件作为建模基本单元，根据不同电路拓扑结构进行组合，完成设备级和系统级建模。根据建模的详细程度分类，常见的开关器件级模型主要有详细开关模型和简化的系统级模型。详细开关模型可以准确反映开关本身物理特性和功率损耗［13］，但模型复杂程度高，且参数不易获得，仅适用于仿真精度要求很高的离线仿真。简化的系统级开关模型则采用更为简单的等效支路来描述开关通断响应。常规电磁暂态仿真中常采用理想开关模型和大/小二值电阻模型［4］即可满足精度要求，但在基于FPGA 的小步长实时仿真中，上述两种建模方法会存在开关动作时间修正的插值算法问题［14］和开关动作后反复求解网络节点导纳矩阵的问题，计算时间较长，仿真效率难以满足实时性要求。

L/C等效恒导纳开关模型用一个小电感/电容来等效开关的导通/关断状态［15］，如图5 所示（通常等效电容支路会串联一个阻尼电阻消除开关切换时的数值振荡），其中：Ls为开关闭合时的等效小电感；Cs为开关关断时的等效小电容；Rs为开关断开时等效电容支路中的串联阻尼电阻；i(t)和u(t)分别为当前时步t的开关支路电流和电压；Ih_on和Ih_off分别为开关组在导通和关断状态下的离散化伴随电路的历史电流源项；Yon和Yoff为开关导通和关断状态下对应的离散化电路的等效电导，是开关模型出现在网络导纳矩阵中的唯一部分。通过合理取值电感和电容参数，开关状态变化可由历史电流源的值来表示而导纳矩阵不变，避免了占用大量FPGA 计算资源重新求逆的问题，仿真步长足够小时可忽略开关插值的影响［16］。但在仿真规模较大、开关数较多的情况下，单纯采用L/C 等效模型建模仍会导致模型求解复杂度呈指数级提升，且在硬件资源约束下仿真规模有限。

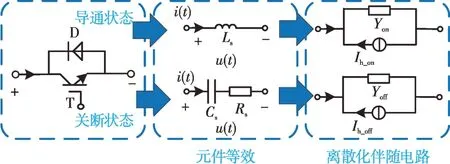
图5 L/C等效恒导纳模型Fig.5 L/C equivalent constant admittance model

除了上述基本建模方法，也有研究提出了基于戴维南/诺顿等效［17］和解耦等效［18］方法实现电力电子变压器和直流变压器模型的简化降维。针对模块化多电平换流器，有研究通过算法切换实现了高精度仿真并减少了内部节点数量，实现了模型计算提速［19-21］。这些方法为基本建模方法的优化改进提供了解决思路，但是尚未有应用于ANPC换流器电磁暂态建模与实时仿真的实例。

综上可知：外特性建模法复杂程度较低，在大规模电力系统仿真场景下具有较高的仿真效率，但其忽略了装置内部特性，难以适用于仿真精度要求较高的场景；开关器件级建模法精度较高，但模型计算复杂度较高，计算时间较长，难以满足实时性要求。

2 ANPC三电平桥臂离散化伴随电路

在构造用于节点分析算法的离散化伴随电路时，不同数值解法对仿真结果和模型表达有很大影响。电磁暂态计算程序中通常采用隐式梯形积分法以满足数值计算的稳定性和准确性，但同样存在数值振荡和求解计算复杂问题。后退欧拉法在电路参数高频变化的仿真场景下稳定性更优，不会出现数值振荡问题［22-23］，在亚微秒级的仿真步长下具有和梯形法相似的精度，离散化电路表达式也更加简单，因此更适用于ANPC 三电平换流器小步长实时仿真场景。

常规型ANPC 三电平桥臂单元内包含IGBT-二极管开关组和电容元件。根据电磁暂态计算方法，设置仿真步长Δt，用数值算法对元件的特性方程进行差分化，得到等效电导和历史电流源并联形式的离散化等效电路结构。

电容元件的电磁暂态计算电路构造如图6 所示，其中：C为元件电容值；Vk和Vm分别为元件支路端节点k、m的节点电压；YC和Ihc分别为离散化伴随电路的等效导纳和历史电流源；ukm和ikm分别为电容支路的电压和电流。

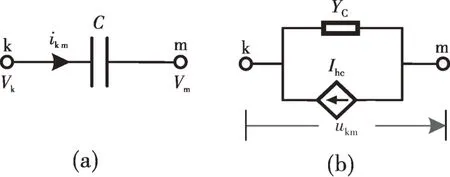
图6 电容支路及其暂态计算电路Fig.6 Capacitor branch and its transient calculation circuit

基本伏安关系方程为：

应用后退欧拉法进行离散化求解：

式（2）可以看作一个值为YC=C/Δt的等效电导与值为Ihc=-Cukm(t-Δt)/Δt的历史项电流源并联的诺顿等效电路，如图6（b）所示。

IGBT-二极管开关组（IGBT 与其反向并联二极管）可以视为用L/C等效电路描述的双向导通开关。根据图5 的L/C 等效恒导纳开关模型，分别列写使用后退欧拉法离散化得到的开关闭合和断开时的特性方程：

式中：i(t-Δt)和u(t-Δt)分别为开关支路电流和电压在上一时步（t-Δt）的历史值。

由式（3）可得不同开关状态下对应图5 的离散化电路等效参数的表达式，历史电流源项分别为：

导通和关断时的等效导纳值分别为：

通过合理设置Ls和Cs的取值，使开关组导通和关断状态时的等效导纳值相等，即满足Yon=Yoff=Y0，可得到模型的恒定导纳值Y0，这样导纳矩阵不会随着开关状态切换而改变，避免了节点分析法计算流程中重新形成导纳矩阵的问题。对比梯形积分法得到的元件等效参数可知，后退欧拉法表达式减少了求解历史电流源项时的加法器和乘法器计算单元的资源消耗，基于后退欧拉法构造离散化伴随电路可提升仿真效率和节约计算资源。

综上，ANPC 三电平桥臂单元的离散化伴随电路整体构造如图7所示，其中：电路中的节点编号为α、β、γ、1、2、3；Iα、Iβ、Iγ、I1为外部网络在边界节点的注入电流；Ihs1—Ihs6为6 个开关组的历史电流源项；Ihc1和Ihc2为上下两直流侧电容的历史电流源项；Y0为6个开关组的等效导纳，YC1和YC2为直流侧电容的等效导纳。

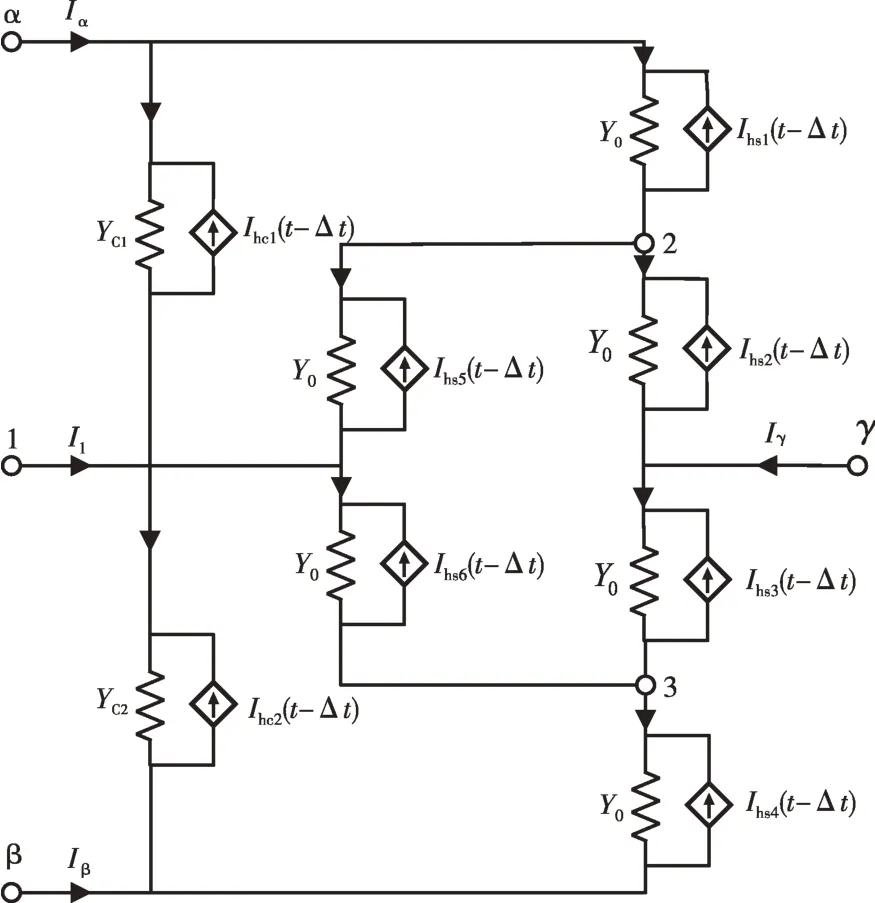
图7 ANPC三电平拓扑伴随电路Fig.7 Associated discrete circuit of ANPC three-level topology

3 基于诺顿等效的降维建模方法

3.1 ANPC三电平单元诺顿等效模型

由图7构造的离散化伴随电路可以看出，在每一时步的网络解算中，电路具有时不变性。该电路可以将节点分为与外部网络直接有电气连接的边界节点和模块内部节点，边界节点为α、β、γ、1，内部节点为2 和3。令电流流入节点的方向为正方向，对仿真时步t的ANPC桥臂单元伴随电路列写网络方程，如式（6）所示，其中YC1、YC2、Y0仅与仿真步长和固定的电感电容取值有关。

式中：Vα、Vβ、Vγ、V1、V2、V3为网络各节点对应的节点电压。

将节点电压方程按照内外节点划分，用分块矩阵的形式来表达，可以改写为：

式中：下标EX 代表外部节点集，IN 代表内部节点集；V为节点电压列向量；J为伴随电路等效历史电流源在各节点的合并注入量；I为外网络注入边界节点的注入电流列向量；Y11、Y12、Y21、Y22为网络的不定节点导纳矩阵。

根据快速嵌套并行求解算法消去内部节点，得到网络Ward等值的表达式为：

其中

式中：Yeq为节点消去后的网络等效导纳矩阵；Jeq为节点消去后剩余节点的历史电流源注入项。

上述表达式体现了网络内部节点消去后等值到边界节点的等效导纳和注入电流效果。将上述Ward等值表达式变换为诺顿等值形式，选取中性点节点1为参考节点，消去Yeq和Jeq中参考节点对应元素，即得到ANPC 三电平桥臂单元面向参考节点的多端口诺顿等效参数表达式，其对应的与外部网络组成的整体电路结构如图8所示。

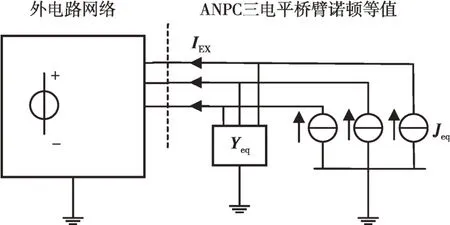
图8 ANPC三电平单元的诺顿等值电路Fig.8 Norton equivalent circuit of ANPC three-level unit

将降阶后的诺顿等效电路代入外电路网络进行一个步长的电磁暂态网络求解，得到桥臂边界节点注入电流IEX，即可通过Ward等值表达式得到边界节点电压VEX。根据边界节点信息，可以结合开关状态进一步还原反解出内部节点电压和支路电流的信息，完成整个内部网络的迭代计算。

基于该等效方法，网络内部节点作用全部等效到边界节点，实现了网络方程矩阵降维和计算简化，对于矩阵计算维数和仿真节点有限的FPGA小步长仿真平台而言，既节约了计算资源，提高了求解速度，又通过节点降维提升了仿真规模上限。

3.2 单元内部电气信息反解与元件状态更新

反解内部网络主要是通过求解单元内部电路的节点电压和支路电流值，更新迭代离散化伴随电路中的元件历史电流源项，用于下一时步仿真计算的初始化。

将推导的诺顿等效电路代入外电路进行整体网络求解后，可以求得边界节点电压VEX和外电路网络对边界节点的注入电流IEX，由此得到内部节点2和3的节点电压反解表达式为：

完成单元内部电路电气信息反解后，即可对离散化伴随电路中的元件参数进行更新并初始化下一时步的计算数据。

电容元件的历史电流源项更新仅需要电容所在支路的电压，用两端节点电压信息（Vk-Vm）即可求解。

IGBT-二极管开关组的历史电流源项与所在支路的电压、电流和通断状态有关。支路电压同样为两端节点电压之差；在离散化伴随电路中规定电流正方向，开关组支路电流可通过基尔霍夫电流定律进行求解。

开关组的通断状态判断由IGBT触发信号和二极管状态决定，基本的判断逻辑如下：当触发信号为1，或当触发信号为0且二极管处于正向导通状态时，开关组处于导通状态；当触发信号为0且二极管处于反向关断状态时，开关组处于关断状态。

元件参数更新完成后即可开始下一时步的仿真计算流程，此时已仿真累计时间T变为T+Δt，直至T到达仿真总时间TFINAL，仿真结束。综上，基于诺顿等效的ANPC 三电平换流器电磁暂态建模和仿真流程如图9所示。

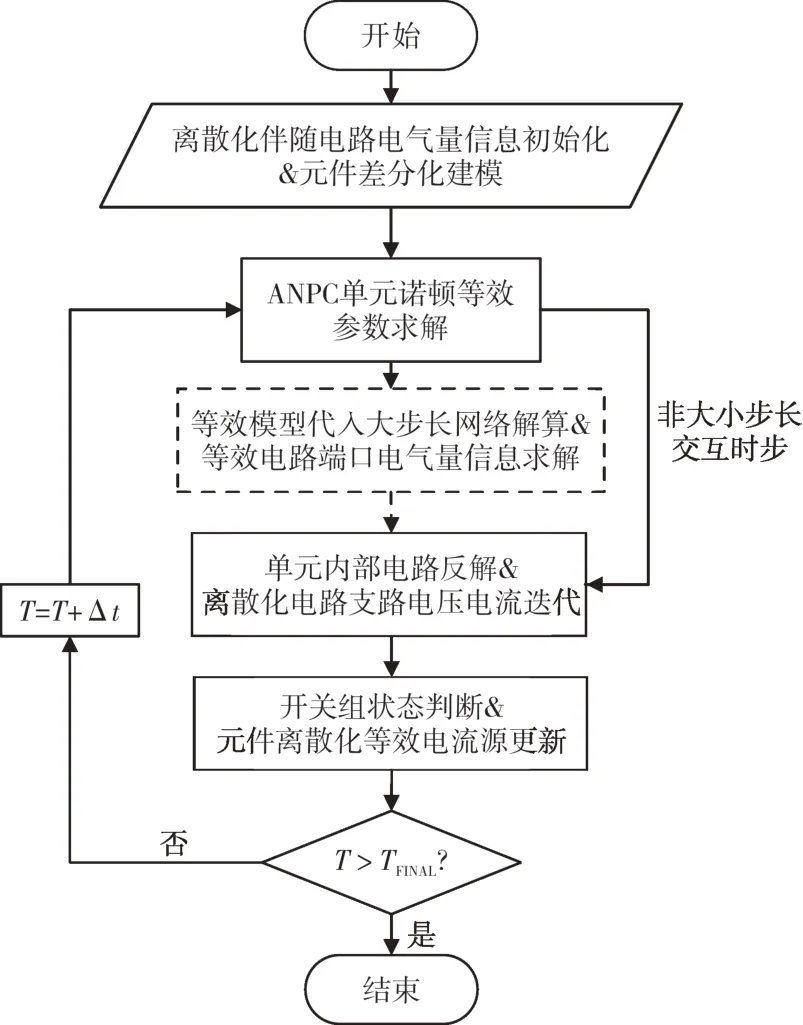
图9 ANPC三电平换流器等效建模及仿真流程Fig.9 Equivalent modeling and simulation flow of an ANPC three-level converter

4 仿真验证

4.1 ANPC三电平换流器仿真模型构建

为验证等效模型的仿真精度和加速性能，按照相同电气参数和仿真配置，在MATLAB/Simulink平台中搭建如图2所示的ANPC三电平换流器系统的电力电子开关详细模型和本文所提出的等效模型，仿真系统的详细参数见表2。本算例采用三电平ANPC 并网逆变器加入dq解耦的典型电压-电流双闭环控制［24］，换流器采用PWM（脉冲宽度调制）双向载波调制。控制器框图如图10 所示，其中：ud和uq分别为dq坐标系下d轴和q轴的网侧前馈电压，ud*和uq*为对应的电压参考值；PI为比例积分环节；ωCFud和ωCFuq分别为电压外环的d轴和q轴解耦项，消除耦合后得到电流内环d轴和q轴的参考值iLd*和iLq*；ωLFiLd和ωLFiLq分别为电流外环的d轴和q轴解耦项，消除电流耦合项后得到dq坐标下的电压调制波，经坐标变换后得到abc坐标下的调制波用于PWM调制，最终得到三相的各IGBT 管的触发信号T1i—T6i（i∈｛a，b，c｝代表A、B、C三相）。

表2 ANPC三电平换流器仿真系统参数Table 2 Parameters of simulation system of an ANPC threelevel converter

4.2 模型仿真精度分析

在搭建的详细模型和等效模型的测试系统中，仿真步长为2 μs，分别设置换流器系统在稳态运行工况和暂态运行工况下的仿真实验，对比观测两种模型的响应波形，以验证本文所提等效模型的精度和动态响应性能。

4.2.1 稳态运行工况

换流器系统在非并网状态下达到稳态运行工况时，交流侧出口三相电压波形以及交流侧负载电流波形如图11 所示。可以看到：系统算例中的电压和电流波形吻合程度较高，出口侧相电压输出为三种电平，最大的相对误差为0.71%；交流侧负载电流波形最大相对误差为2.11%，且输出波形谐波含量较低。上述结果验证了等效模型的精度。

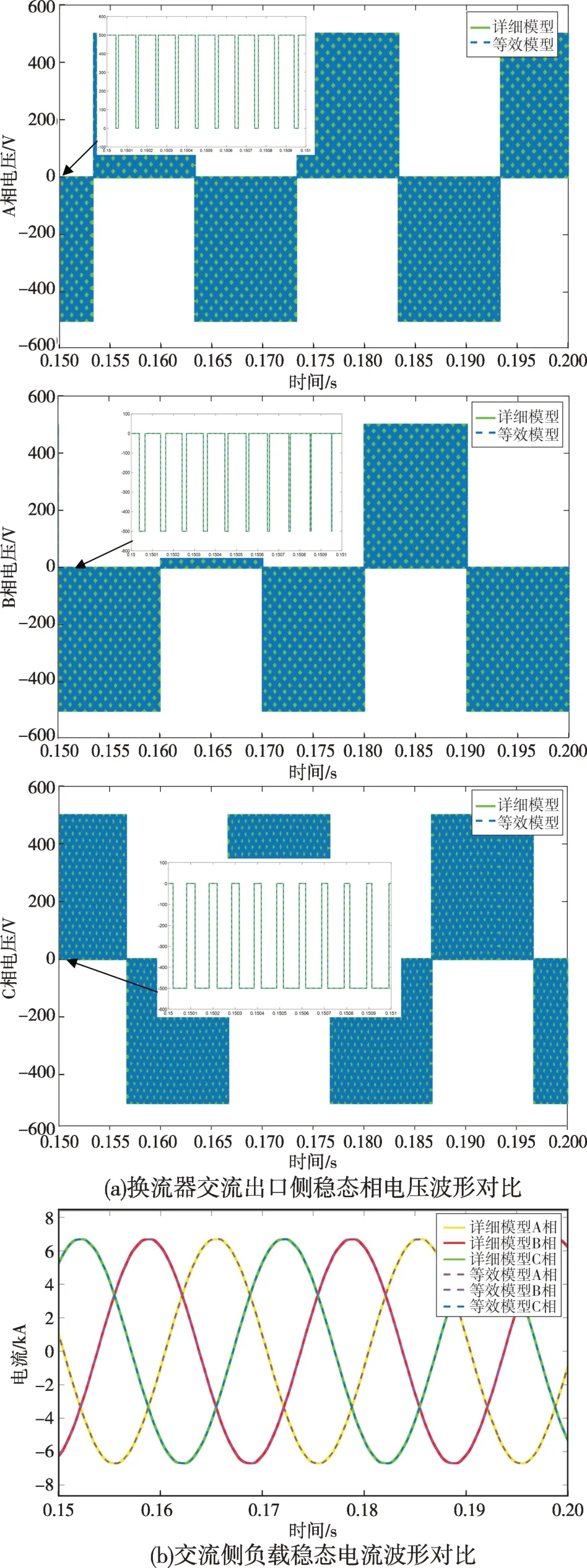
图11 换流器系统仿真模型稳态工况输出波形Fig.11 Output waveforms of converter simulation model under steady-state working condition

4.2.2 暂态运行工况

进一步验证等效模型的在暂态运行工况下的动态响应性能。在t=0.9 s 至t=0.95 s，换流器发生交流出口侧A 相接地短路故障，换流器出口侧的电压、电流和交流网侧的电压、电流动态响应结果如图12 所示。上述暂态故障过程中，换流器出口侧和电压交流侧系统的A 相母线电压大幅下降，而换流器出口和网侧电流均有不同程度增大，在故障清除后各部分电压、电流响应均恢复到原正常运行工况。系统暂态扰动响应结果和过渡过程均符合预期，如图13 所示，对比详细模型与等效模型，暂态工况换流器出口母线电压波形输出结果拟合度较好，验证了等效模型对于系统动态响应的正确性。

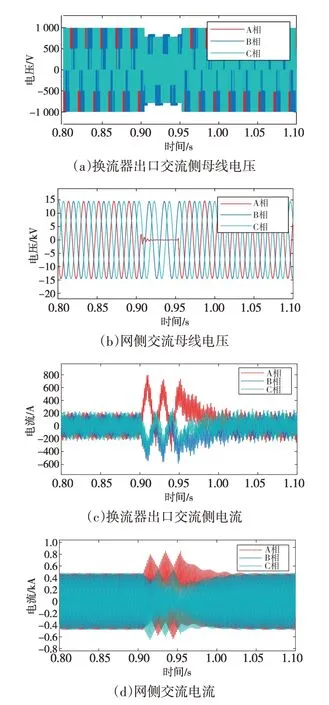
图12 换流器系统仿真模型暂态工况响应波形Fig.12 Response waveform of converter simulation model under transient working condition

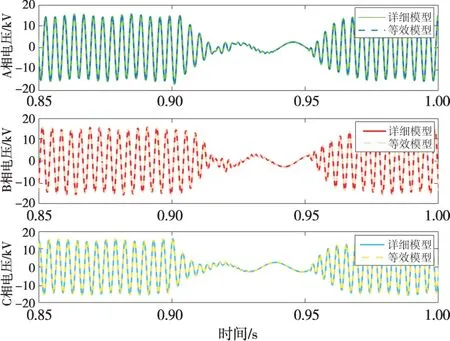
图13 暂态工况换流器出口母线电压波形对比Fig.13 Comparison of waveforms of bus voltage at converter outlet under transient operating condition

4.3 模型仿真速度和稳定性分析

以上述搭建的ANPC 三电平换流器系统为新能源场站出口基本单元，构建含有多个换流器的仿真算例，分别用详细模型和等效模型进行仿真测试，比较二者的CPU仿真用时，以验证本文所提等效模型的提速性能。不同换流器组数下，大网络系统模型的仿真用时对比和加速比结果见表3。可以得出，等效模型对比详细模型有较明显的提速效果，且电网仿真规模越大提速效果越明显，验证了本文所提等效模型在大规模小步长实时仿真场景下的适用性。

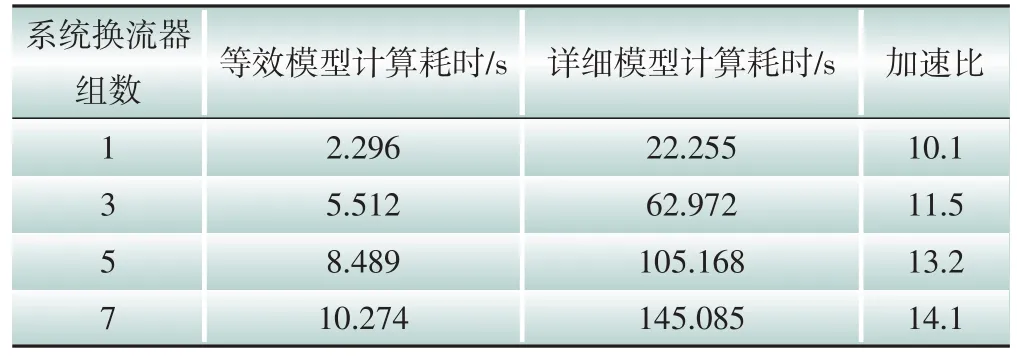
表3 模型的CPU仿真时间对比Table 3 Comparison of CPU simulation time of the model

在仿真效率分析中搭建含7 组ANPC 变流器等效模型的多机并联系统拓扑，如图14 所示，其中：PCC 为系统公共连接点；Ug为系统交流网侧电压源，Rg和Lg分别为其内电阻和内电感；LL1—LL7和RL1—RL7分别为传输线路的等效电感和等效电阻；Lf1—Lf7和Cf1—Cf7分别为每组滤波电路的滤波电感和滤波电容；U1—U7为各组换流器系统的直流侧电压。设置并联机组在t=1.5 s时并于交流网侧（不考虑加入并网控制策略），两种模型下PCC 电压Vpcc的仿真结果对比如图15 所示。可以看出，系统电压响应波形拟合结果较好，验证了本文所提等效模型在网级应用层面的仿真稳定性和精度。

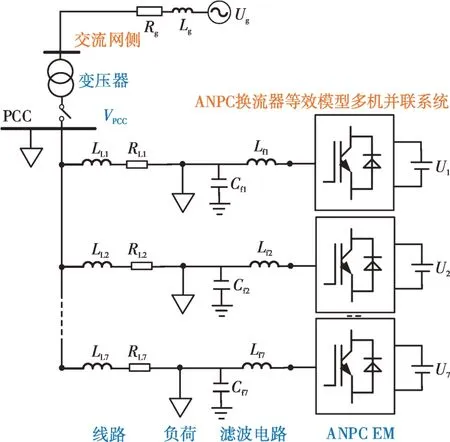
图14 含7组ANPC换流器等效模型的多机并联系统Fig.14 A parallel system with 7 equivalent models of ANPC converters

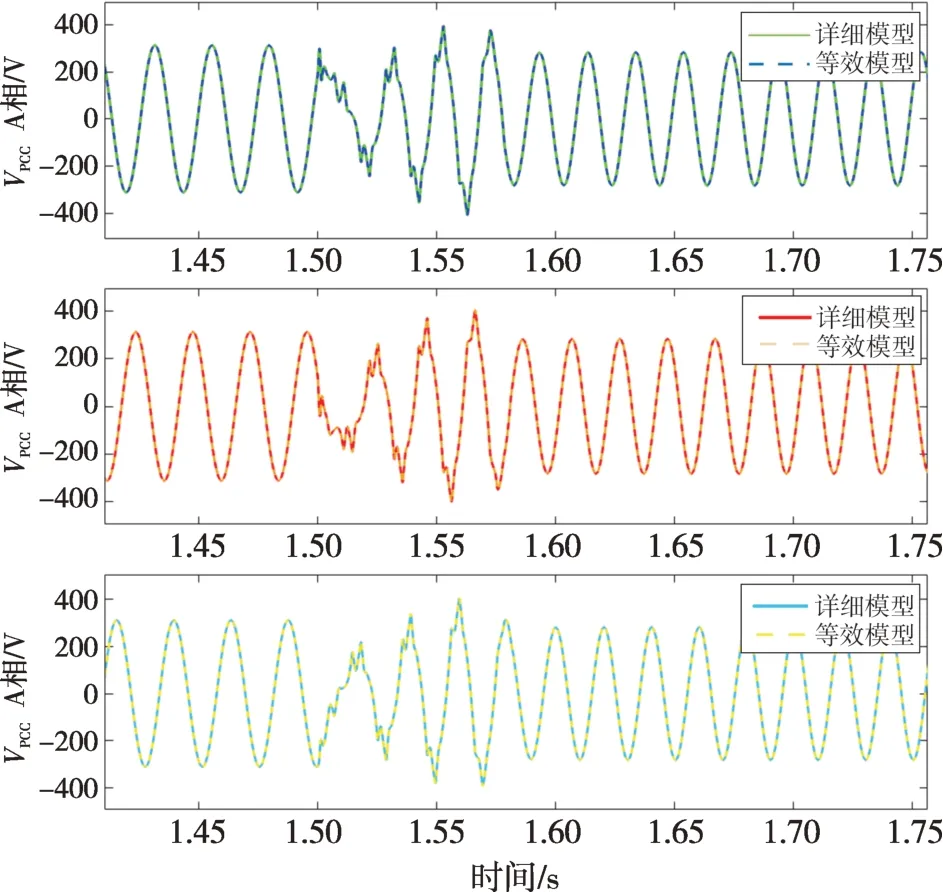
图15 ANPC换流器多机并联系统仿真结果对比Fig.15 Comparison of simulation results of paralleled ANPC converters

5 结语

本文提出一种适用于小步长实时仿真的ANPC 三电平换流器高效电磁暂态模型，并给出了具体建模方法。首先构造ANPC 三电平换流器桥臂的离散化伴随电路，并基于Ward等值方法建立多端口诺顿等效电路，实现了单元内部节点的消去和降维。基于该等效方法，设计了包括诺顿等效参数求解、网络方程解算、单元内电路信息反解、历史电流源项更新的ANPC 三电平换流器系统的完整电磁暂态计算流程，在不损失精度的前提下实现了模型解算复杂度的降低和模型规模的压缩。

在MATLAB/Simulink平台上分别搭建ANPC三电平换流器的开关详细模型和本文所提等效模型的仿真系统，通过算例测试，验证了所提等效模型在保证开关器件级建模仿真精度的同时，具有较好的仿真提速效果。所提出的模型设计完全可映射于FPGA 小步长仿真平台架构，下一步拟依据该建模方法实现基于FPGA 的ANPC 三电平换流器实时仿真系统设计，以完善本研究内容。对于大规模电网仿真场景下的其他多电平复杂拓扑的电力电子装置建模，本文提出的等效降维思路也具有参考价值。