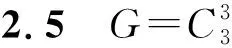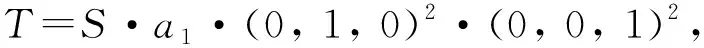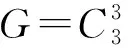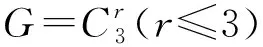初等3-群中表出达文波特常数的极小集
2024-01-24赵小越吴雄华
赵小越,吴雄华
(天津工业大学 数学科学学院,天津 300387)
0 引言
从20世纪60年代阿贝尔群上的零和问题开始被研究,近几十年来取得了迅速发展[1-2].令G是一个加法有限阿贝尔群,由有限阿贝尔群基本定理,|G|=1或G≅Cn1⊕…⊕Cnr,其中1 达文波特常数D(G)是零和理论的起点之一,也是本文的研究对象之一.达文波特常数是一个最小的常数t,使G上每个长度大于等于t的序列S都有非空的零和子列.令A(G)是G上所有极小零和序列构成的集合,B(G)是G上所有零和序列构成的幺半群,记G上空序列1为幺半群B(G)上的单位元.高维东等人为了统一表达零和不变量定义了dΩ(G)[3].对于Ω⊂B(G),定义dΩ(G)是一个最小的整数t,使G上每个长度大于等于t的序列S在Ω内都有子列.若这样的t不存在,则令dΩ(G)=∞,因此1∈Ω时dΩ(G)=0.故在后文中,只讨论Ω⊂B(G){1}的情况.文献[4][5]继续研究了dΩ(G)及其相关变量的零和问题. 是G0上的一个序列.序列中元素用符号· 连接,通常情况下可以省略.令 vg(S)是g在S上的重数; 若σ(S)=0,则称S是一个零和序列; 若S没有非空零和子列,则称S是无零和序列; 对于g∈G0,若vg(T)≤vg(S),则称T是S的一个子列,记作T|S; 若非空零和序列S的每个真子列都是无零和序列,则称S是极小零和序列. 显然空序列 1不是极小零和序列,因此A(G0)⊂B(G0){1}.若dΩ{S}(G)>dΩ(G),则称序列S在Ω内是不可去序列.Ω是dΩ(G)=t的最小Ω当且仅当Ω中任意序列都是不可去序列. 引理2.1[4]设p是一个素数,当G是以下群时,有D(G)=M(G) : (1)r(G)≤2 ; (2)G是一个有限阿贝尔p-群. 引理2.2[3]令Ω,Ω′∈B(G){1} ,若Ω⊂Ω′,则dΩ′(G)≤dΩ(G) . 引理2.3Ω是dΩ(G)=D(G)的最小Ω当且仅当Ω上的每个序列S都在群G上存在一个D(G)长的序列W,且W所有的非空零和子列和S形式相同. 证明由文献[4]中引理5.7显然得到. 引理2.4G=C3⊕C3时A(G)是dΩ(G)=D(G)的最小Ω. 证明因为C3≅Z3,下面对G=Z3⊕Z3展开证明.由Ωmin定义,Ωmin⊂A(G*),因此只需证A(G*)⊂Ωmin,即任意S∈A(G*)都有S∈Ωmin.由引理2.1,D(G)=5.显然长度为D(G)的极小零和序列一定属于Ωmin,所以任意长度为5的极小零和序列都属于Ωmin,因此只需证任意S∈A(G*),|S|≤4,都有S∈Ωmin. 当S∈A(G*),|S|=1时,S只能为序列(0,0),令T=S·(0,1)2·(1,0)2,则T的零和子列只形同于S.即S∈A(G*),|S|=1,有S∈Ωmin. 当S∈A(G*),|S|=2时.若存在序列T,使T的零和子列只形同于(1,0)(2,0),那么也存在序列T′,使T′的零和子列只形同于(0,1)(0,2),称这样的性质为对称性.由对称性,只需讨论以下三个极小零和序列,分别为 S1=(1,0)(2,0);S2=(1,1)(2,2);S3=(1,2)(2,1). 则存在 只含有形同于S1,S2,S3的极小零和序列.因此对于任意S∈A(G*),|S|=2,都有S∈Ωmin. 当S∈A(G*),|S|=4时,设S=a1·a2·a3·a4.由S∈A(G*),序列中有且仅有两个线性无关元,设a1=(1,0),a2=(0,1) .若a3或a4=(1,0),则 S=(1,0)2(0,1)(1,2). 令T=S·(0,1) ,则T的零和子列只与S形同.若a3=a4≠a1≠a2,则 S=(1,0)(0,1)(1,1)2. 令T=S·(0,1),则T的零和子列只形同于S.此时不存在四个元素互不相同的情况.由对称性和序列的无序性,长度为4的极小零和序列都属于Ωmin. 综上,任意S∈A(G*) ,|S|≤4,都有S∈Ωmin.G=C3⊕C3时A(G)是dΩ(G)=D(G)的最小Ω得证.该定理证毕. 若S∈A(G*)且|S|=1,则S只能为(0,0,0).令T=(0,0,0)(1,0,0)2(0,1,0)2(0,0,1)2,则T的极小零和子列只与S形同.所以长度为1的极小零和序列属于Ωmin. 若S∈A(G*)且|S|=4,设S=a1·…·a4.由S∈A(G*),序列中至少有两个线性无关元.若序列中仅有2个线性无关元,类似上述方法,由引理2.4存在极小零和子列只与S形式相同的序列.若序列中有3个线性无关元,设a1=(1,0,0) ,a2=(0,1,0),a3=(0,0,1),则S=a1·a2·a3·(2,2,2).令T=S·a1·a2·a3,则T的极小零和子列只与S形同.由对称性,长度为4的极小零和序列都属于Ωmin. 若S∈A(G*)且|S|=5,设S=a1·…·a5.由S∈A(G*),则S至少有2个线性无关元.若S中仅有2个线性无关元,设a1=(1,0,0),a2=(0,1,0),则a3,a4,a5可由a1,a2线性表出.类似上述方法,由引理2.4,存在极小零和子列只形同于S的序列.若序列中有3个线性无关元,令 a1=(1,0,0),a2=(0,1,0),a3=(0,0,1) 若a4或a5=aj,j∈[1,3],不妨设a4=(1,0,0).此时 S=(1,0,0)2(0,1,0)(0,0,1)(1,2,2). 令T=S·a2·a3,则T的极小零和子列只与S形同.若a4=a5≠aj,j∈[1,3].由S∈A(G*) 得 S=(1,0,0)(0,1,0)(0,0,1)(1,1,1)2. 令T=S·a1·a2,则T的极小零和子列只与S形同.若序列5个元素互不相同,只需讨论以下两种情况: S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(2,1,0),T=S·a4·(2,1,0); S=(1,0,0)(0,1,0)(0,0,1)(1,0,1)(1,2,1),T=S·a1·(1,2,1). 上述T的极小零和子列均只与它所对应的S形式相同.由对称性和无序性,长度为5的极小零和序列都属于Ωmin. 若S∈A(G*)且|S|=6,设S=a1·…·a6.由S∈A(G*),序列中有且仅有3个线性无关元,令 a1=(1,0,0),a2=(0,1,0),a3=(0,0,1). 若a4=a1=(1,0,0),a5=a2=(0,1,0),由S∈A(G*)有 S=(1,0,0)2(0,1,0)2(0,0,1)(1,1,2). 令T=S·(0,0,1),则T的极小零和子列只与S形式相同.若a4=a1=(1,0,0),讨论以下两种情况: S=(1,0,0)2(0,1,0)(0,0,1)(0,1,1)(1,1,1),T=S·(0,1,0); S=(1,0,0)2(0,1,0)(0,0,1)(0,1,2)(1,1,0),T=S·(0,0,1). 存在序列T,它的极小零和子列只形同于对应的S.若a4=a5≠a1≠a2≠a3,讨论以下情况: S=(1,0,0)2(0,1,0)(0,0,1)(0,1,2)(2,0,1),T=S·(1,0,0); S=(1,0,0)2(0,1,0)(0,0,1)(0,1,1)(1,2,2),T=S·(0,1,0). 存在T的极小零和子列只与对应的S形式相同.若序列中6个元素互不相等,讨论以下情况: S=(1,0,0)(0,1,0)(0,0,1)(1,1,0)(0,1,1)(1,0,1),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(1,1,0)(2,1,1)(2,0,1),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(1,1,2)(1,0,1)(0,1,2),T=S·(0,0,1); S=(1,0,0)(0,1,0)(0,0,1)(1,1,2)(1,2,2)(0,2,1),T=S·(0,1,0); S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(1,0,1)(1,1,2),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(1,0,2)(1,1,1),T=S·(0,0,1); S=(1,0,0)(0,1,0)(0,0,1)(1,2,2)(0,2,1)(1,1,2),T=S·(0,1,0); S=(1,0,0)(0,1,0)(0,0,1)(1,2,2)(2,1,2)(2,2,1),T=S·(2,1,1). 上述T的极小零和子列均只与它所对应的S形式相同.由对称性和无序性,长度为6的极小零和序列都属于Ωmin. 证明r=1时,G=C3,显然成立.由引理2.4和引理2.5,定理显然成立.该定理证毕.
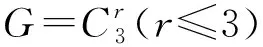
1 定义及符号介绍


2 定理的证明