基于混合启发式算法的快递末端选址路径优化研究*

孙睿男,初 翔,陈 昱,闫明宁

(1.大连海事大学航运经济与管理学院,辽宁 大连 116026;2.大连海事大学综合交通运输协同创新中心,辽宁 大连 116026)

1 引言

近年,快递数量快速增长,给快递末端网点及末端配送环节带来了巨大的压力。目前,快递配送末端由于各自为政的配送模式,导致配送成本居高不下,而共同配送模式可以有效降低末端配送成本[1]。因此,在共同配送模式下,合理规划快递网点选址及配送路径问题具有重要的研究意义。

有关选址路径问题研究中,王琪瑛等[2]研究了电动车辆选址路径问题;胡大伟等[3]研究了两阶段的选址路径问题;Arslan[4]从客户覆盖范围的角度研究了选址路径问题。Kinay等[5]对充电站选址问题进行了研究。Ozbaygin等[6]对动态路径问题进行了研究。上述选址路径研究多假设客户需求为已知的情况,而在快递实际配送过程中,一般其派件量为已知,而收件量为不确定的情形,关于随机选址路径问题相关文献也较为丰富,如需求不确定型[7-9]、时间不确定型[10]、距离不确定型[11]、场景不确定型[12]及多重因素不确定型[13]。

针对末端快递选址路径的研究文献也较为丰富,如de Giovanni等[14]针对快递货运路径规划问题进行研究,建立了综合考虑车辆容量、时间窗约束的数学模型。Bergmann等[15]对城市配送最后一公里问题进行研究,建立了考虑车辆容量的数学模型。许闯来等[16]对快递配送网络进行研究,在建立模式时考虑了配送车辆载荷约束。裴利奇等[17]研究了快递中转站选址问题,建立了考虑快递中转站容量和配送车辆载荷约束的数学模型。Li等[18]对快递企业配送包裹问题进行了研究,在建模时加入了载具容量约束。Yan等[19]建立了城市动态快递调度模型,在模型中也考虑了容量约束。姬杨蓓蓓等[19]针对快递末端配送网络优化,建立了考虑车辆载荷约束的选址路径模型。可以看出,以上对快递末端网点配送的研究都只考虑配送车辆的载重约束,均未考虑快递配送与物流配送之间的差异。快递配送与物流配送之间的区别主要有以下2点:(1)快递配送除了对快件重量有限制之外,对快件的体积也有一定的约束。如贺冰倩等[21]对快递收派路径规划问题进行了研究,在建立模型时同时考虑了快件容量和体积约束。(2) 在物流配送中,末端配送基本使用轻型厢式货车作为配送载具;而快递配送方式大多为快递员进行末端配送,配送成本多为人工成本。

梳理上述文献可知,相关研究已取得一定成果,但还存在以下几点不足:(1)大部分文献并未考虑到快递同时收派件,且需求随机的情况;(2)配送车辆返回策略均为返回原出发网点,该返回策略易造成较高的配送成本;(3)所建模型大部分未考虑快递末端配送的实际特性,即快递配送与物流配送之间的差异性。

因此,基于以上几点,本文结合共同配送模式特点,考虑快递配送与物流运输之间差异性,以人工成本为目标函数,引入随机机会约束解决需求随机问题,基于最近网点返回策略,建立包含快件重量、体积以及配送员最大时长等约束的数学规划模型;并设计基于遗传算法和自适应大邻域搜索ALNS(Adaptive Large Neighborhood Search algorithm)算法的混合启发式算法,对随机需求下快递网点选址路径问题进行研究。所得结论可为快递企业提供相应管理启示,并为后续对随机需求选址路径研究提供方法参考。

2 共同配送随机LRP模型建立

2.1 问题描述

本文所研究问题可描述为在某区域内存在多家快递企业的快递网点,后文简称为网点,客户点和网点的位置已知,所有节点集合A=W∪C,网点集合为W={1,2,…,n},si为网点i的建设成本,1≤i≤n,网点最大容量为Qw(w∈W),实际容量为Qi,客户点集合为C={n+1,n+2,…,n+m}。每个客户点派件量是确定的,收件量为不确定的情况,dwj和dvj分别为客户点j(n+1≤j≤n+m)的派件重量和体积,rwj和rvj分别为客户点j的收件重量和体积,假设每个客户的收件量相互独立且均服从相同泊松分布,E(rwj)和E(rvj)分别为收件重量和体积的期望值。dij为任意网点i和客户点j之间的距离,dj(j+1)为任意客户点j和客户点j+1间的距离,其余变量均用此方法表示。K={1,2,…,α}为配送车辆集合,V为配送车辆行驶速度。假设配送时,车辆一直保持匀速行驶,Qk和Vk分别为配送车辆k(1≤k≤a)的最大容量和最大体积,Qijk为配送车辆k在网点i和客户点j之间的载量,Vijk为车辆k在网点i和客户点j之间的配送体积。cd和cr分别为配送员派件和收件的单位人工成本,cs为单位时间配送的人工成本,Tp为配送员单次最大配送时长。决策变量Zi∈{0,1},若Zi=1,表示在网点i建立快递网点,否则相反;决策变量Yij∈{0,1},若Yij=1,表示客户点j被网点i服务,否则相反;决策变量Xijk∈{0,1},若Xijk=1,表示配送车辆k从网点i经过客户点j,否则相反。快递员从网点出发进行派送,派送完成后返回距离最近的网点。

如何合理地选择快递网点及安排派送路径是本文研究核心,主要目的是降低成本,因此以网点选址路径总成本为目标函数,建立两阶段双层规划模型。第1阶段中上层模型考虑网点选址成本最低,包含建设成本和人工成本,下层模型考虑配送距离最短。因客户点收件量为不确定的随机变量,所以有可能出现第1阶段所选网点容量无法满足客户点的实际需求量或配送车辆容量和体积无法满足客户点的需求量的情况,从而导致预优化阶段方案失效。此时就需要第2阶段重新优化,重优化阶段采用失败点前序点重优化策略,以此确定末端快递网点建设及配送路径规划,减少物流整体配送成本。

2.2 数学模型

2.2.1 上层模型

假设某一预优化方案中客户点集合C,均由某一网点对其派送,在服务完前j-1个客户点后,现要确定客户点j+1是否也由该网点进行派送,采用随机机会约束机制进行判断,此时该网点的剩余载荷量Qj=Qw-(dw1+dw2+…+dwj)-(rw1+rw2+…+rwj),因收件量rj为随机变量,此时通过随机机会约束机制判断是否由该网点服务客户点j,即P{rwj≤Qj-dwj}≥α,α为预先设定的风险偏好值,其表示决策者在不确定情况下对风险的可接受程度。若决策者对风险的接受程度不高,更想保证预方案的成功率,则α应取较高值;反之,α应取较低值,α∈(0,1],dj和rj分别为客户点j的派件量和收件量。式(1)表示上层模型目标函数,包含了快递网点的建设成本和人工成本;式(2)表示网点建设数量的约束条件;式(3)表示网点载荷量的随机规划约束;式(4)表示决策变量,为0-1变量。目标函数式中Z、Y和X均为所求的决策变量。

(1)

s.t.

(2)

P{rwj≤∑i∈WYijQj-dwj}≥α,∀j∈C

(3)

Yij∈{0,1},Zi∈{0,1},∀i∈W,∀j∈C

(4)

2.2.2 上层模型随机机会约束等价处理

上层规划模型中,约束条件式(3)可以推导为确定型等价形式,式(3)可变为:

(5)

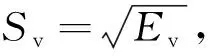
(6)

假设常数τ为α的分位点,则式(6)可转化为:

(7)

因此,由式(5)和式(7)可知:

Sv·τ+Ev≤T

(8)

T=Q-∑i∈W∑j∈CdwjYij

(9)

将期望和标准差均代入式(8),得:

(10)

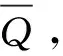
(11)

(12)

2.2.3 下层模型

同样地,车辆k按顺序对客户进行配送,现判断客户点j+1是否由车辆j服务,则车辆在客户点j和客户点j+1之间的实际载荷量Qj(j+1)=∑j∈CQ0jk-(dw1+dw2+…+dwj)-(rw1+rw2+…+rwj),其中∑j∈CQ0jk为车辆k初始载荷和体积,即车辆所需配送的所有点派件量之和。此时,若车辆继续对客户j进行服务需满足rwj≤Qj(j+1)k-Qojk+dwj,引入随机机会约束,即P{rwj≤Qj(j+1)k-Qojk+dwj}≥α,α∈(0,1]。同理,其体积随机约束为P{rvj≤Vj(j+1)k-Vojk+dvj}≥α。

式(13)为下层规划目标函数,以总配送距离最小为目标;式(14)和式(15)分别表示配送车辆的载荷与体积的随机机会约束;式(16)表示配送员最长配送时间约束;式(17)表示每个客户仅被服务一次;式(18)表示避免网点之间相互配送;式(19)表示每个客户仅被一个快递网点服务;式(20)表示节点流量平衡约束;式(21)表示配送车辆从网点出发时的负载量等于该网点所服务客户的派件需求总和;式(22)表示配送车辆在各节点负载量;式(23)表示配送车辆回到快递网点时的负载量等于该网点所服务客户的收件量需求总和;式(24)和式(25)表示车辆负载量约束;式(26)和式(27)为决策变量之间的关系,分别表示当点i被选为建设快递网点,则必有客户点j由网点i配送和只要存在客户点j由网点i配送,则网点i必被选为建设快递网点;式(28)表示决策变量,为0-1变量。

(13)

s.t.

P{rwj≤∑i∈W∑j∈C(XijkQijk+Xj(j+1)kQj(j+1)k)-

Q0jk+dwj}≥α,∀k∈K

(14)

P{rvj≤∑i∈W∑j∈C(XijkQijk+Xj(j+1)kQj(j+1)k)-

Q0jk+dvj}≥α,∀k∈K

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

0≤Qijk≤QkXijk,∀i∈W,∀j∈C,∀k∈K

(24)

0≤Qj(j+1)k≤QkXi(j+1)k,∀j∈C,∀k∈K

(25)

(26)

Yij≤Zi,∀i∈W,∀j∈C

(27)

Xijk,Xj(j+1)k∈{0,1},∀i∈W,∀j∈C,∀k∈K

(28)

2.2.4 下层模型随机机会约束等价处理

随机约束规划式(14)可转化为:

P{rwj≤Qk-∑i∈W(XijkQijk+Xj(j+1)kQj(j+1)k)+

∀j∈C,∀k∈K

(29)

推导过程与上层模型推导过程中式(5)～式(12)同理,快件重量的随机机会约束确定型等价形式可转化为:

(30)

T=Qk-∑j∈CQ0jk+

∑i∈W(Xijkdwj+Xj(j+1)kdwj)

(31)

同理,快件体积的随机机会约束确定型等价形式可转化为:

(32)

T=Vk-∑j∈CV0jk+

∑i∈W(Xijkdvj+Xj(j+1)kdvj)

(33)

2.2.5 重优化阶段

重优化阶段中,对于选址问题网点容量无法满足的情况,选择添加新的网点进行后续配送,而现有对随机需求路径问题失败点处理方法主要有失败点返回策略、失败点前序点返回策略和失败点重优化策略3种。

如图1所示,A、B为快递网点,图中实线为预优化阶段路径,虚线为重优化阶段路径,8个客户点中,客户点2,4和6为失败点,预优化阶段路径如图1a所示。

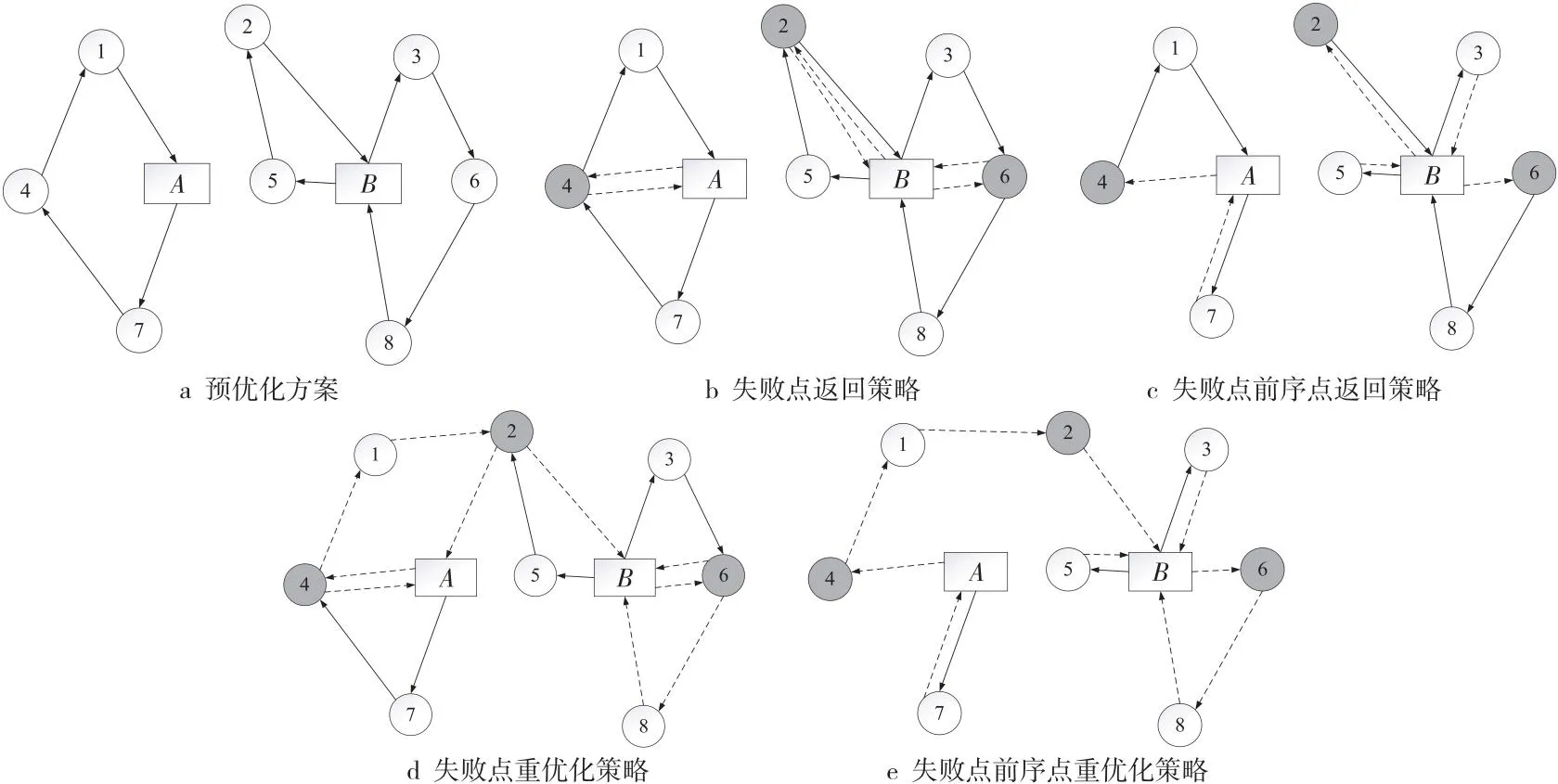
Figure 1 Failure point return policy图1 失败点返回策略

(1)失败点返回策略,如图1b所示,配送车辆在客户点2,4和6不满足条件无法配送时,车辆返回原快递网点,再按预优化安排进行后续配送。

(2)失败点前序点返回策略,如图1c所示,配送车辆在失败点4的前序点1,预先对车辆剩余载荷能否满足失败点4的需求进行判断,若车辆剩余载荷能满足后序点需求则对其服务,否则,在失败点前序点就返回原配送网点再继续配送,这种情况下,其配送路径长度一定小于失败点返回策略。

(3)失败点重优化策略,如图1d所示,配送车辆在失败点返回原出发网点,对于失败点及其预优化方案中后续客户点进行重新统一规划,设计配送方案生成重优化路径,再按重优化阶段路径方案进行配送。

总结以上几种返回策略中,失败点返回策略操作最为简单,但其配送路径距离较长,前序点返回策略未考虑到后续点的统一优化,无法保证整体路径最优。因此,将失败点前序点返回策略和失败点重优化策略相结合组成失败点前序点重优化策略,并在返回规则上进行改善,结合共同配送模式特点,配送车辆在返回网点时,无需返回原配送网点,选择距离最近的网点返回,可缩短配送路径的距离。

如图1e所示,配送车辆在失败点4的前序点7通过判断其后序点无法满足配送需求时进行返回,统计所有失败点及其后续点,重新设计后续客户点配送方案,生成重优化阶段路径安排。

3 混合自适应大邻域搜索遗传算法

针对双层模型解空间大、计算复杂等特性,本文设计混合自适应大邻域搜索遗传算法进行求解。将自适应大邻域搜索算法嵌入遗传算法中,每一代进化时先用遗传算法寻优;再将遗传算法种群中最优个体作为自适应大邻域搜索算法的初始解进行求解;最后,通过“个体替换”操作将自适应大邻域搜索算法所得的新解替换掉遗传算法种群中适应度最低的解,生成新一代种群,以达到改善种群质量的目的,以此不断迭代,直至算法结束。

本文所设计的混合自适应大邻域搜索遗传算法结合了2种算法的优点,即通过遗传算法的选择算子、交叉算子和变异算子等来提升自适应大邻域搜索算法的全局搜索能力,降低算法陷入局部最优解的概率;而自适应大邻域搜索算法的破坏算子和修复算子也可以加强遗传算法的局部搜索能力,并通过引入自适应机制,自适应更新算子权重,使其在每次迭代的时候都可以选择当前最优的算子进行解的变换,强化每一代的求解质量。改进后的混合自适应大邻域搜索遗传算法可以更好地在全部解空间中寻优,得到更满意的解。具体的算法流程如图2所示。

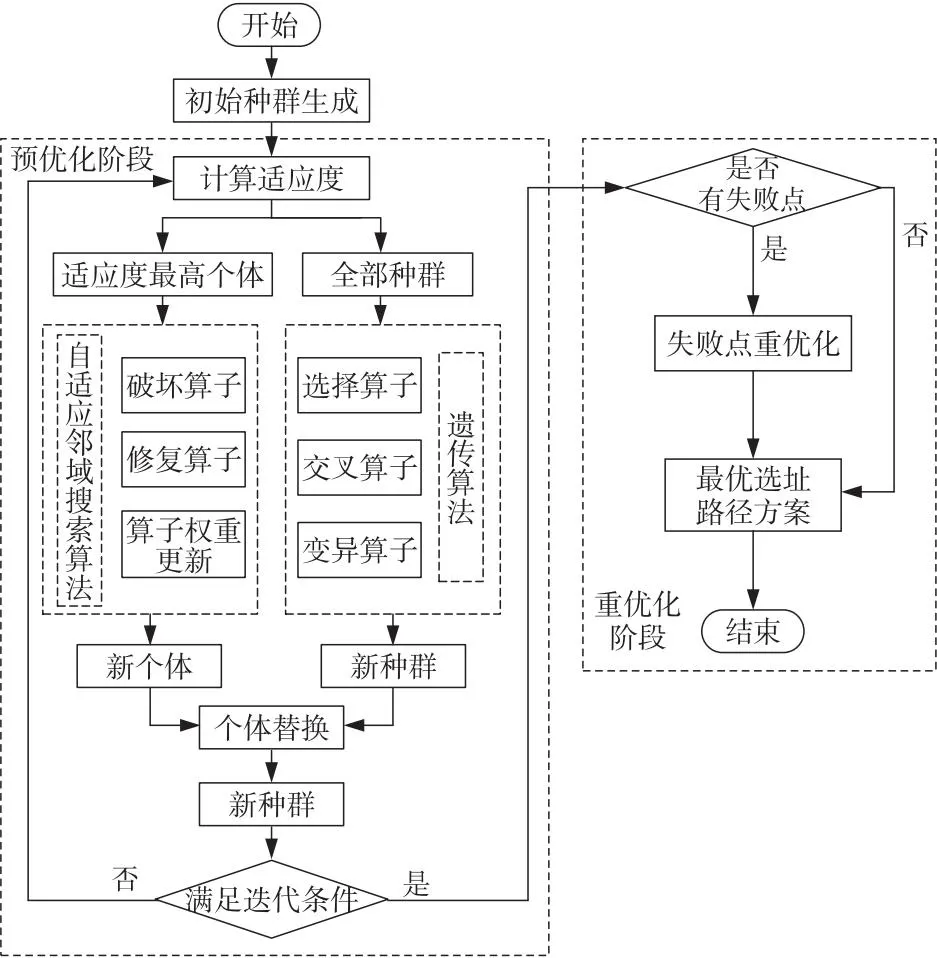
Figure 2 Flow chart of hybrid adaptive large neighborhood search genetic algorithm图2 混合自适应大邻域搜索遗传算法流程

3.1 编码及解码方式

算法采用整数编码的方式,将全部客户需求编号点打乱顺序存入染色体编码方案列表中,作为配送的服务顺序。

解码过程包括2步:第1步根据随机机会约束机制及快件的重量、体积约束将客户分配给配送员,如不满足该约束条件,则为该需求点增加新的快递员进行服务,直至为所有需求点都分配好快递员;第2步根据每辆配送车辆首尾客户到快递网点的距离确定车辆的出发网点和返回网点。

具体以图3为例,其中1～10为客户需求点,a、b和c为3个配送网点,将客户点打乱顺序加入列表中,即为染色体编码方案;解码首先根据编码方案列表中的顺序为配送员分配客户,当分配到第4个客户,即客户6时,发现不满足约束条件,为客户6及后续客户点安排新的配送员进行配送服务;将已分配好的配送路径{1,3,2}以列表的形式加入二维列表route中,并根据配送路径中起始客户和末尾客户,选择最近的网点作为其始末网点,加入二维列表depot中,确定最终的始末配送中心,即配送员从网点a出发进行派送,先后服务客户点1,3和2后返回最近网点b;以此类推,确定最终的染色体解码方案。

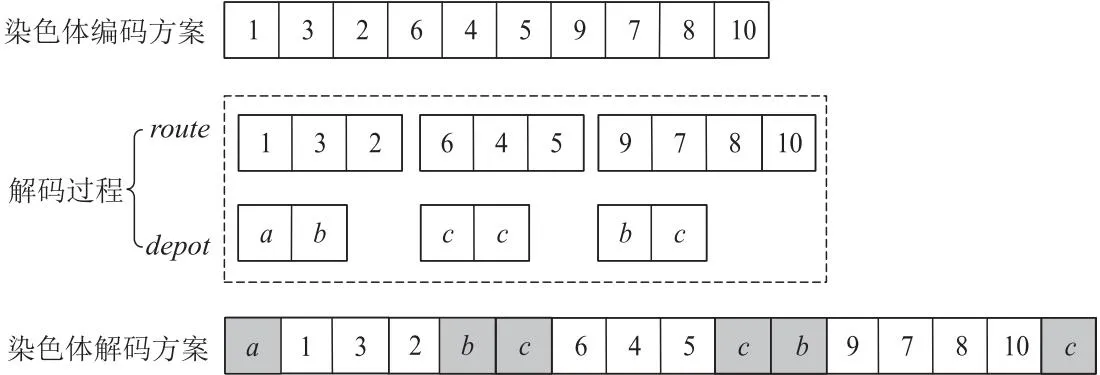
Figure 3 Coding and decoding modes图3 编码及解码方式

3.2 初始种群生成

随机生成一个种群规模为popesize的初始种群,popesize为预先设定好的数值,通过计算每个个体的适应度,将适应度最大的个体作为自适应大邻域搜索算法的初始解,对该个体进行邻域搜索。全部初始种群就作为遗传算法的初始解进行迭代,再通过个体替换,即将自适应大邻域搜索算法所得的新个体替换掉遗传算法所得新种群中适应度最小的个体,生成新一代种群。

3.3 适应度函数

先给出上层选址模型的初始解,将其代入下层模型进行求解,得出的配送路径规划方案再反馈到上层模型中,以上层模型的目标函数式(1)的倒数作为算法个体的适应度函数fs,如式(34)所示:

(34)

由式(34)可知,目标函数值F1越优,其染色体个体适应度fs越大。

3.4 遗传操作

遗传操作在整体算法中起到全局搜索的作用,通过选择、交叉和变异等操作,可以避免整体算法陷入局部最优解的情况:

(1)选择算子:采用二元锦标赛选择策略,即每次在父代种群中随机选择2个不同的个体,通过比较2个个体的适应度大小,将适应度较大的个体加入新的种群中,重复n_select次数。

(2)交叉算子:需考虑到子代染色体中是否包含重复基因,考虑到该因素,下层模型采用OX交叉法。即随机选择2个染色体作为父代染色体,选择其中一个染色体的一串基因直接复制到子代染色体相同位置,再从另外一个父代染色体中按顺序将不同于子代染色体中已有的基因复制到子代染色体中,所得的新染色体即为子代染色体。该方法巧妙地避免了子代中出现重复基因的情况。

(3)变异算子:在变异过程中,同样考虑子代染色体重复基因的情况,采用二元突变的方式,即随机从种群中选取一个染色体作为父代染色体。在已选择的父代染色体中随机选择2个不处于相同位置的基因点,然后交换该2点的基因值,得到的新染色体即为子代染色体。

3.5 自适应大邻域搜索操作

自适应大邻域搜索算法主要是增强算法的邻域搜索能力,其中邻域搜索算子有很多种,本文引入2种破坏算子及3种修复算子,通过不断地破坏和修复个体来搜索邻域解。

(1)破坏算子。

① 随机破坏算子:即在个体染色体中随机选取宽度在[d_min,d_max]中的一段基因序列,存入remove_list中,以备修复操作时使用。

② 最差破坏算子:即移除一定范围引起目标函数增大的需求点,通过分别计算移除每一个需求点后目标函数的减少量,对需求点进行排序,按照一定比例移除需求点集合。

(2)修复算子。

① 随机修复算子:与随机破坏算子原理相同,即在已破坏个体中,随机将remove_list中的基因序列插入到个体中,形成新解。

② 贪婪修复算子:根据remove_list中需求点顺序,依次将列表中需求点插入使目标函数增量最小的位置,直至remove_list列表为空。

③ 后悔修复算子:计算remove_list中需求点插入到待插入个体序列中L个次优位置时目标函数的变化,选择使目标函数变化最大的需求节点及其最优位置。

(3)算子权重更新策略。

每次迭代都更新权重在处理大规模问题时所需时间太长,可以通过合理设置p的值来平衡求解时间和权重更新的及时性之间的关系。因此,每迭代p次更新一次算子权重作为混合大邻域搜索遗传算法的权重更新策略。权重更新表达式如式(35)所示:

(35)

其中,W(α)表示算子α每次更新权重;p表示算子更新衰降系数;S(α)表示算子α的总奖励得分,与算子的被选择次数和使用该算子后产生的邻域解的质量有关;t(α)表示算子被选择的次数。

4 数值实验与实例分析

4.1 算法参数及性能对比

(1)参数确定。

本文研究的随机选址路径问题目前没有统一的标准通用算例,因此选择Prodhon提出的经典选址路径问题标准测试集(http://prodhonc.free.fr/Instances/instances_us.htm)中部分算例对算法参数及性能进行测试。分别选取测试集中名称为coord20-5-1(算例包含20个客户点,5个备选中心)、coord50-5-1(算例包含50个客户点,5个备选中心)和coord100-5-1(算例包含100个客户点,5个备选中心)的算例对算法进行参数分析,通过调整参数取不同的值,用算法对上述3个算例分别求解5次,对3个算例中最优解对应的参数求平均数,取该平均数作为最终的参数值。最终确定的参数最优值如表1所示。

表1中包含以下参数:PC为交叉算子概率;PM为选择算子概率;N_select为进行选择操作时,选择种群的比例;Rand_d_max为随机破坏算子的最大上限,Rand_d_min为随机破坏算子的最低下限;Worst_d_max为最坏破坏算子的最大上限,Worst_d_min为最坏破坏算子的最低下限;Regret_n为后悔修复算子中取次优位置的个数。

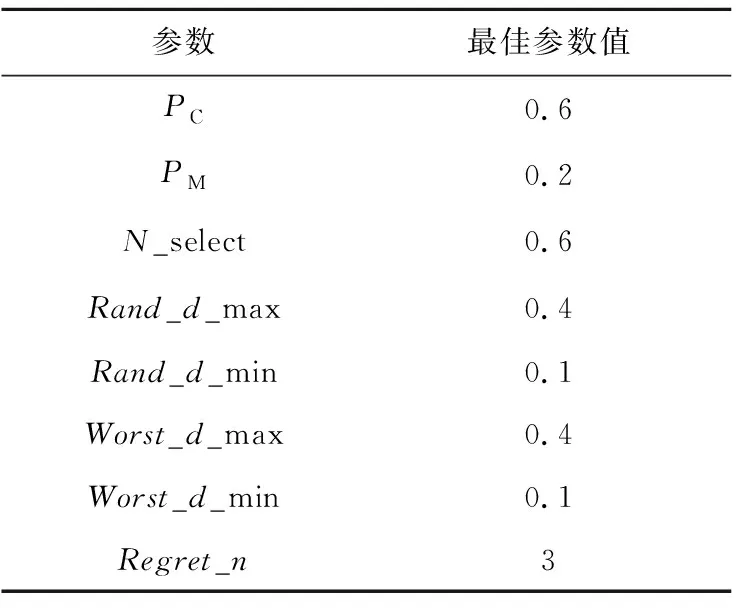
Table 1 Optimal values of parameters表1 参数最优值

(2)算法性能对比。

为了测试混合算法性能,设置目标函数包含配送中心和车辆的固定成本及运输成本,分别用自适应大邻域搜索(ALNS)算法、传统遗传算法GA(Genetic Algorithm)以及本文设计的混合自适应大邻域搜索遗传算法ALGA(Adaptive Large neighborhood search and Genetic Algorithm)运行5次,对运行结果进行对比。所得结果如表2所示,其中,BS表示已知最优解,Best表示算法运行5次的最优解,Gap表示当前算法所得结果与最优解之间的差距,Ave表示平均数据。

由表2可知,本文所设计的ALGA算法在客户规模为20时可找到最优解;对比各算法的Gap值衡量算法性能,ALGA算法的Gap值平均为1.50%,相对于GA算法的2.40%和ALNS算法的2.89%,说明ALGA算法性能相对其他2种启发式算法更优。

(3)算法收敛性对比。

为了分析算法的收敛情况,选取coord20-5-1算例,记录每一代种群最优解并绘制算法收敛图,进行算法收敛性分析。

从图4可以看出,在50代以内,GA算法和ALGA算法收敛速度相近,但其在50代后陷入了局部最优解;ALNS算法虽然一直稳步收敛,但整体迭代速度较慢;本文提出的ALGA算法结合GA和ALNS 2种算法的优点,不仅在求解初期迭代速度快,并且全程持续稳步收敛,在400代附近找到最优解。相比于改进前的算法,本文的ALGA算法收敛到最优解的速度最快。

Figure 4 Comparison of algorithm convergences图4 算法收敛对比图

4.2 实例验证

本文选取某市范围内快递网点作为研究对象,对数据进行整理,可描述为该区域内有3家快递企业,6个已有网点作为备选网点(如表3所示),20个配送需求点(如表4所示),网点容量均为1 000 kg,配送车辆载重为200 kg,容量为1.5 m3,单位时间配送的人工成本为15元,车辆行驶速度为15 km/h,收派件单件提成为0.5元。在进行选址路径规划时,需求点收件量是不确定的,只有派送到该点才能知道具体的量。根据收派件的数据预先设置需求点的收件量服从λ=10的泊松分布。

采用标准遗传算法(GA)和改进的混合自适应邻域搜索遗传算法(ALGA)对上述实例数据分别计算10次,对比运算结果。

由表5的实验结果可以看出,改进的混合自适应邻域搜索遗传算法的最优解和平均解都优于标准遗传算法,并且,混合自适应大邻域搜索算法的标准差值较标准遗传算法低了2.23,由此可知混合自适应邻域搜索遗传算法的稳定性更强。

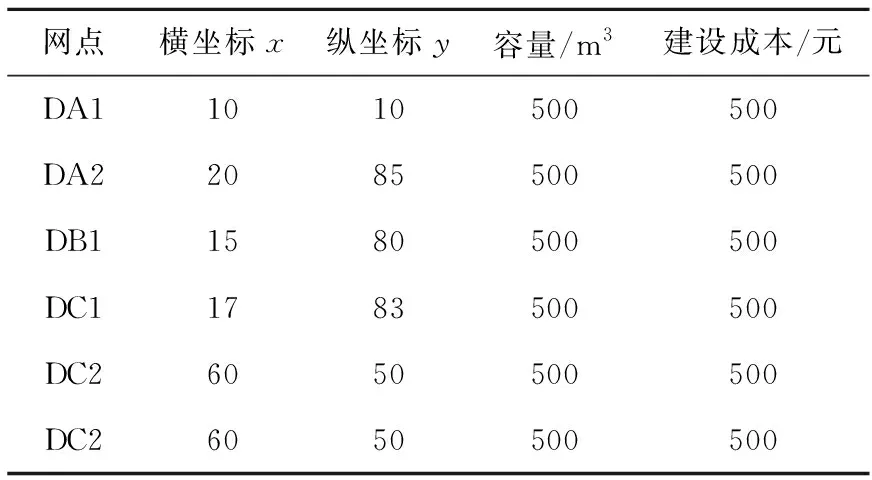
Table 3 Parameters of alternative outlets表3 备选网点参数表

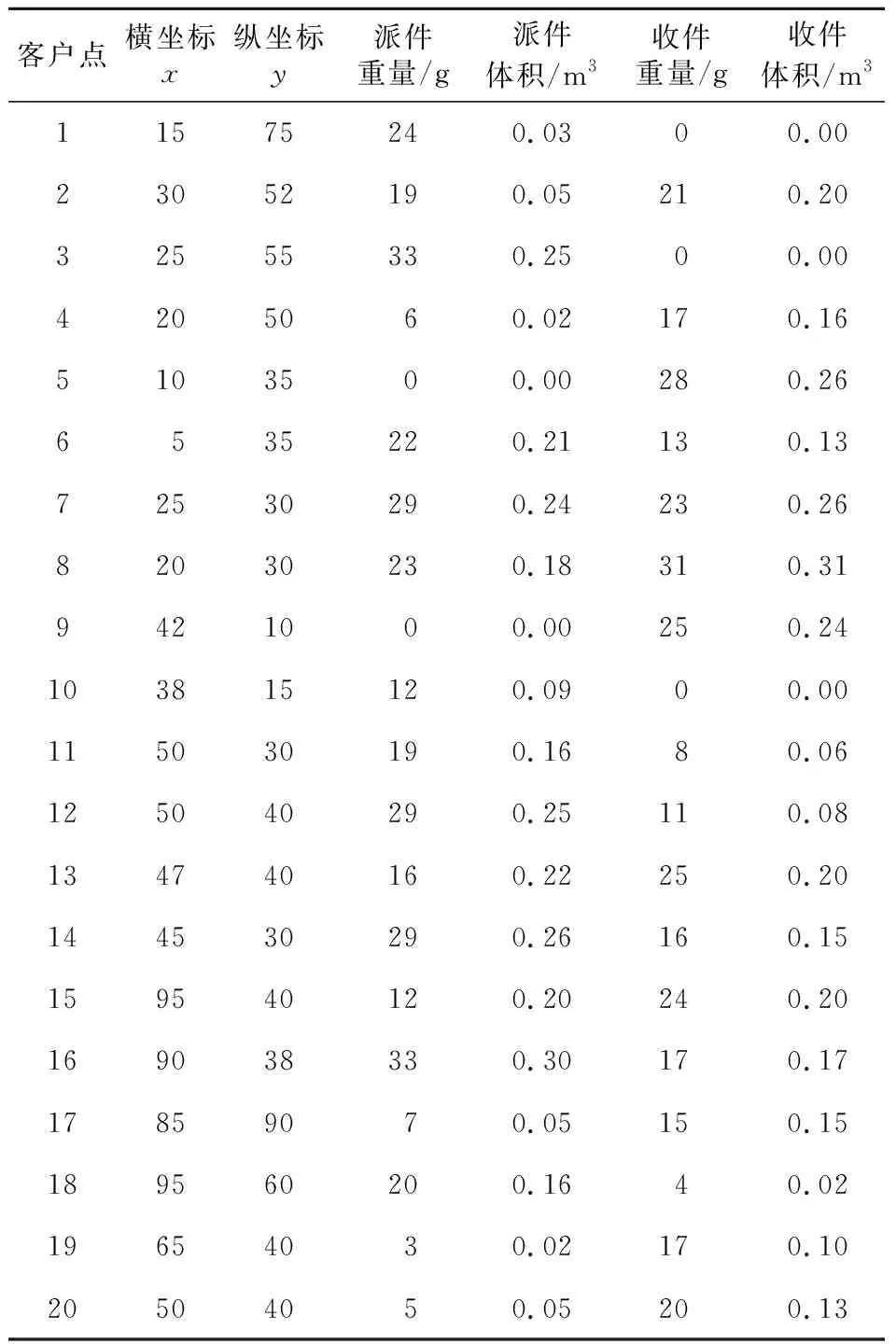
Table 4 Customer point parameter 表4 客户点参数

Table 5 Example results comparison表5 结果对比

上述各组算例及实例结果表明,改进后的混合算法相对于标准遗传算法及自适应大邻域搜索算法,在求解质量和求解速度方面都有明显提升。这是因为遗传算法局部搜索能力较弱,而在遗传算法中引入局部搜索能力较强的邻域搜索算法来提升算法种群质量,可以结合2种算法的优点,增强算法的全局搜索能力。该算法可以有效解决物流配送选址路径求解耗时长和求解质量差的问题。采用本文改进的混合遗传算法,在同等客户规模情况下,能够有效减少快递配送物流成本,提升整体配送效益。

4.3 灵敏度分析

实验1风险偏好值α的取值影响。

研究随机问题时,通常采用引入随机机会约束的方法进行求解,因而预设置的风险值α值得探讨,α的设定既要保证模型成本在可接受的范围内,同时也要满足模型中的载荷等约束。因此,本节采用上述实例数据,设置α的值从0.1到1.0,分别对模型进行求解,根据求解结果分析风险值α对模型成本的影响。

实验结果如表6所示,可以看出当偏好值α在0.4～0.7时,模型总成本较低,当偏好值α为0.6时,模型成本最优。分析其原因,可能是由于当α值设置较小时,更趋向于一次派送较多的客户,导致配送路径失败,从而产生更多的成本;当风险值α设置较大时,随机机会概率较小,一次配送所服务的客户数量较少,造成成本较大。因此,过大或者过小的偏好值都会引起配送成本的升高,所以建议物流企业决策者在制定配送方案时要根据实际情况选取风险偏好值,避免选取较高或较低的偏好值,保证物流配送成本最优。

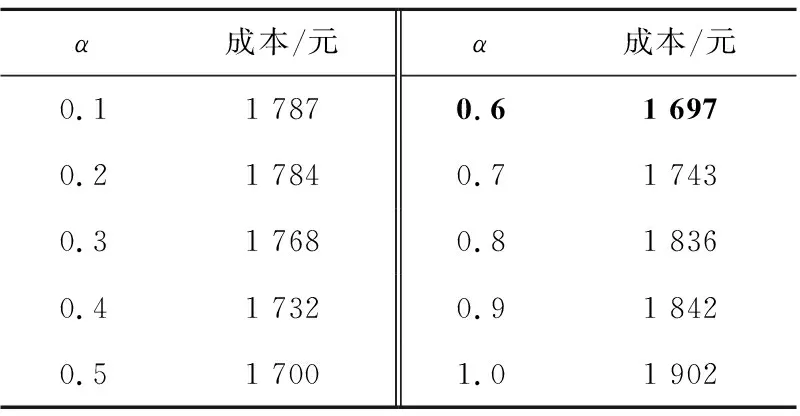
Table 6 Influence of preference value on the results表6 偏好值对结果的影响

实验2收派件数量的影响。

在实际的快递派送过程中,顾客的收派件数量经常发生变化,因此,本文探究收件与派件的数量对网点选址路径决策的影响。以上文中实例数据为例,控制收派比为不同值,分别对其求解,根据结果进而分析收派比的影响。

由表7中数据的变化可以看出,随着收派比的增加,模型整体成本呈先下降后上升趋势。分析其原因,本文所研究的问题为收件数量为不确定的情况,因此当收派比较高时,随着实际收件量的增加,预先规划的路径失败的概率增大,从而导致成本上涨;而当收派比较低时,实际收件量较少,低于所设收件量的期望值,并且在总量不变的情况下,一定的收件量可以提高派送车辆空间利用率,所以在总量不变的情况下,过低的收件量也会导致成本升高。由此可以得出收派件数量比值的变化对配送方案的制订有着重要意义,建议物流决策者在制定路径配送方案时应充分考虑收件与派件之间的数量关系。

Table 7 Influence of dispatch ratio on results表7 收派比对结果的影响

实验3不同返回策略的影响。

为验证最近网点返回策略的合理性,以实例数据为例,对不同返回策略下实例求解结果进行分析。表8给出了2种不同返回策略下的结果,其中,Best为总成本的最优值,CL为总成本,D为配送距离,Gap为CL与Best的偏差值。

Table 8 Influence of different strategies on results表8 不同策略对结果的影响

根据表8结果可知,在对本文实例求解中,2种返回策略对比,最近网点返回策略的成本最优;返回原网点策略相比最近网点返回策略,其实际配送距离较长,因此其末端物流成本也高于最近网点返回策略。以本文数据为例,采用最近网点返回策略可使末端成本降低1.5%,因此本文所采用的最近网点返回策略可以有效降低物流企业配送成本。

5 结束语

本文对共同配送模式下收件量随机的同时收派件的快递网点选址路径问题进行研究。首先,建立所研究问题的数学规划模型,针对模型中的收件量不确定性,引入随机机会约束,生成第1阶段选址路径规划,并提出新的失败点重优化策略解决第1阶段优化失败问题。然后,提出一种混合自适应邻域搜索遗传算法,改进传统遗传算法的局部搜索能力不足的问题,并通过算例证实了混合遗传算法的高求解效率和快速收敛能力。最后,通过数值实验,分析模型风险偏好值、收派件数量之比及返回策略对网点选址路径规划的影响,形成相应的管理启示。并得到如下结论:

(1)所建立的数学优化模型,综合考虑了共同配送、收件需求随机、快递配送的特征,以及最近网点返回策略,虽然使模型求解更为复杂,但更符合快递服务的实际需求。

(2)所设计的混合启发式算法,在传统遗传算法的基础上引入自适应邻域搜索算法来改善每一代种群的质量,有效提升了算法全局搜索和局部搜索的能力,较传统启发式算法具有更好的求解质量和更快的收敛速度。

(3)对风险偏好值的灵敏度分析表明,过高或者过低的偏好值取值都会导致物流成本上升;对收派件比值灵敏度分析表明,随着收派比的增加,模型整体成本呈先下降后上升趋势;对不同返回策略的实验分析表明,多个配送网点在共同配送的基础上,采用最近网点返回策略可以有效地降低快递企业配送成本。

物流企业可以综合考虑以上因素进行配送方案制定,降低末端配送成本。

本文的研究可以为多个快递企业实施多网点共同配送提供较好的选址配送方案,但需要指出的是,研究中并未考虑快递企业可能会受到多重不确定环境及客户时间窗因素的影响。如何在时间窗约束下及多重不确定因素下规划好快递末端配送问题是未来的研究方向。