基于代数粒的聚类方法*

肖振国,陈林书,孙少杰,梅本霞,柳媛慧,赵 磊

(1.湖南科技大学计算机科学与工程学院,湖南 湘潭 411201;2.湖南科技大学外国语学院,湖南 湘潭 411201; 3.湖南警察学院信息技术(网监)系,湖南 长沙 410138)

1 引言

粒计算作为智能计算研究领域中信息处理的一种新理念和新方法,其本质是通过选择合适的粒度来寻找一种较好的、近似的解决问题的方案,并且在此过程中去除繁冗,降低问题求解的复杂性[1,2]。粒化,作为粒计算中的核心工作,主要是将未分组的粒子(细粒度)聚类为分组(粗粒度)。聚类,作为机器学习的最重要任务之一,旨在将相似的对象分组在一个聚类中,它主要包括数据预处理和知识聚类这2个步骤[3]。从这个角度来看,粒计算中的粒化与机器学习中的聚类任务是相同的。近年来,越来越多的研究人员也开始逐渐从粒计算的角度研究聚类方法。

粒计算中的粒度包括3个部分:粒子、粒属性和粒结构。粒子是粒计算的基本计算单元,因其相似性、相邻性和一致性而内部不可区分。粒属性为同一粒度上所有粒子所共有的一组公共特征。粒结构描述了同一粒度上所有粒子之间的结构关系。目前大部分粒计算模型都是基于粒属性进行聚类,而没有考虑粒结构,例如表1中的容差邻域模型[4,5]和粗糙集理论[6,7]。表1中的商空间理论[8,9]和代数商模型[10-12]虽然分别引入了拓扑粒结构和代数粒结构,但仅从粒层上讨论粒度的转换方法,而没有研究相应的粒度聚类方法。事实上,代数粒结构广泛应用于包括数字编码、形式语言、电子电路设计等在内的信息与通信领域。例如,汉明编码是一种以模2运算为代数粒结构的典型应用[12]。但是,目前系统地讨论代数粒结构的文献非常有限。

Table 1 Brief introduction to the research of granular computing and clustering model表1 对粒计算与聚类模型研究的简述

基于以上分析,本文在作者前期工作[10-15 ]的基础上,从粒计算的角度提出一种基于代数结构的聚类方法,主要工作有以下3个方面:

(1)基于代数二元算子,建立代数粒模型,为代数结构的粒度数据提供形式化描述方法。

(2)通过同余关系粒化,从粒计算的角度提出一种基于代数粒的聚类方法,通过粒集的同余划分和粒结构的同态映射进行粒度聚类。该方法为代数结构的粒度聚类提供一种新型方法,从结构上丰富了粒度计算理论。

(3)将基于代数粒的聚类方法与容差邻域模型和商空间模型进行对比分析。实验结果表明,基于代数粒的聚类方法具有更好的结构完备性和应用鲁棒性。

2 相关知识

2.1 粒计算与聚类

粒计算,最早是由Lin[6]在1997年提出的,粒计算被视为与粒子相关的所有理论、策略、方法、技术和工具[2],现已广泛应用于机器学习[16]、知识获取[17]、复杂问题解决[18]、图像处理、模式识别、智能控制、人工神经网络和语言动态系统等领域。作为粒计算的关键工作之一,粒化可以分为变量粒化(聚类)、概念粒化(聚合)和值粒化(量化)。在数据预处理的过程中,粒化将原始数据转换成具有不同行和列语义的表,其中行对应于原始元组的组(粒),列表示关于每个组内原始值的聚类信息。

聚类,是对一组对象进行分组的任务,使同一组(一类)中的对象比不同组(聚类)中的对象在某种意义上更相似。聚类是数据挖掘的主要任务,也是统计数据分析的常用技术,应用于许多领域,包括图像处理[19]、机器学习[20]、服务计算[21]、模式识别、信息检索、生物信息学、数据压缩和计算机图形学。

基于粒属性的聚类,是一种旨在创建聚类树的分层聚类算法,其最终目的是降低维度、冗余和存储需求。目前大多数粒计算聚类方法都是基于粒属性的,例如:容差邻域模型[4,5]基于容差关系进行粒化,并且根据粒属性的值将粒集聚集成类;粗糙集理论[6,7]粒化基于等价关系,粒集根据等价划分被聚类。然而,上述基于粒属性的聚类方法仅考虑粒属性,即它预先假设粒度上的所有粒子都是独立的,它们之间没有任何结构关系。

基于粒结构的聚类,是近年来出现的基于粒结构的粒计算聚类方法,如表1所示。Zhang等人[8,9]提出了商空间理论,将粒结构指定为拓扑结构,通过同余关系进行粒化,为不同粒子之间的变换和分解提供了理论支持。Wang等人[22,23]将粒定义为一个七元组G=(C,Rc,Ri,Ro,B,Ω,Θ),粒结构是由内部关系Rc、输入关系Ri和输出关系Ro组成的开放系统,为粒系统提供了一个强有力的建模概念。 Chen等人[10-12]提出粒计算的代数商模型,将粒结构看作一个代数运算,并通过同余关系进行粒化。但是,上述研究仅将粒结构分别指定为拓扑序和代数运算,而没有从粒计算角度研究相应的聚类方法。

2.2 粒度体系结构

粒度,是粒计算中最基本和最重要的概念。图1给出了论域U={ui|i=1,2,…,P}上的粒度三元组定义(UN,FQ,S),其中,P是论域U中元素个数,粒集UN={vi|i=1,2,…,N}中的粒子vi是U的子集,N表示粒子数量,粒属性FQ={fj|j=1,2,…,Q},Q表示属性数量,粒结构S表示粒集UN上粒子之间的结构关系。

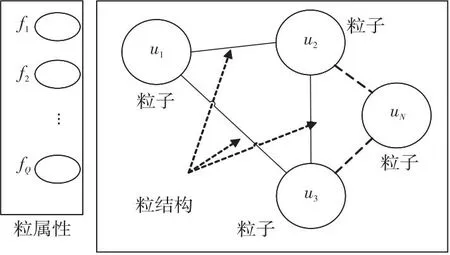
Figure 1 Architecture of granularity (UN,FQ,S)图1 粒度(UN,FQ,S)的体系结构

一般地,问题空间都是从最复杂的原始最细(离散空间上)粒度开始求解,下面提出的新型聚类方法,就是从细粒度到粗粒度进行聚类。因此,下文所指的原始粒度(UN,FQ,S)对应的粒集UN={vi|i=1,2,…,N},就是论域U={ui|i=1,2,…,N}上的最细粒度UN={{ui}|i=1,2,…,N}。

粒属性FQ是所有粒子相互共有的一组特征,目前已有成熟的聚类算法,如划分聚类(k-Means、围绕中心点的划分聚类PAM(Partitioning Around Medoid))、层次聚类(自底向上的层次聚类AGNES(Agglomerative Nesting)、自顶向下的层次聚类DIANA(DIvisive ANAlysis))和密度聚类DBSCAN(Density-Based Spatial Clustering of Applications with Noise),本质上都是基于粒属性离散值的距离度量,进而对样本集进行聚类。基于粒属性的聚类方法,作者在文献[12,15]中另有讨论。

本文不讨论粒属性,仅从粒结构上讨论信息粒化和聚类方法。因此,粒度(UN,FQ,S)可以简单地表示为二元组(UN,S)。并且,由于粒结构作为代数被广泛应用于信息和通信领域,所以UN中的粒结构S被特指为代数二元算子∘(x,y),即粒度简化为二元组(UN,∘)。

2.3 基于粒计算的聚类方法

图2展示了聚类过程的典型步骤,以及本文工作的重点,即从粒计算的角度设计新型聚类方法的框架。图2下层是一个通用的聚类过程,包括从源数据中选择特征、预处理数据、聚类方法选择和验证聚类结果以及在应用中将最终聚类结果解释为知识表示4个步骤。图2上层给出了本文提出的基于代数粒的聚类方法的主要内容,包括代数粒定义的预处理和粒度粗化过程的聚类方法,对应于机器学习视角下的特征选择和聚类方法选择。

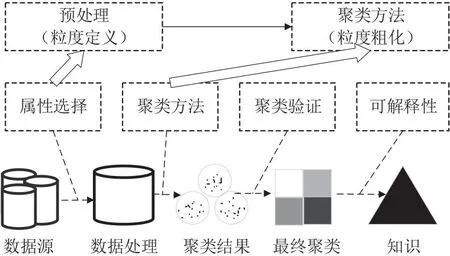
Figure 2 Clustering process from the perspective of granular computing图2 粒计算视角下的聚类过程

图2上层的粒度定义到粒度粗化的过程,本质上是粒计算中的粒化过程,它旨在将未分组的粒子(细粒度)聚集成几个部分(粗粒度),而这也正是粒度聚类过程。例如,35岁、2个月、13天的客户可以被聚类成35岁客户的粗粒度,并且也可以被继续聚类成中年(30～55岁)客户的更粗粒度。在本文的设计中,数据预处理是生成信息粒度,从粒度计算角度看,其目标是在粒化之前的信息格式化和粒度创建。聚类方法对应粒计算的粒化过程,即将具有模糊或不确定性的不同粒子进行聚类。因此,预处理和聚类方法对应于粒化过程中的粒度定义和粒度粗化过程。

3 本文方法

基于图2中的通用聚类框架和新型聚类方法,本节从粒计算的角度提出基于代数粒的聚类方法,主要包括以下任务:

(1) 将具有代数运算关系的粒结构定义为一个二元算子∘,进而定义代数粒为(UN,∘N×N)。

(2) 以同余关系R进行粒化,将粒子集UN聚类到同余划分UM中,粒结构∘N×N同态映射到⊕M×M,从而将代数粒(UN,∘N×N)粒化为粗粒度(UM,⊕M×M)。其中,M表示聚类粒结构⊕M×M的度,即聚类粒集UM的粒子数量。

3.1 粒度建模

粒度是粒计算中一个非常重要的概念,因为粒系统中的孤立粒子没有任何意义,只有当粒子处于由具体粒化规则下的某一粒度上时,它才有意义。在聚类算法的初始阶段,每个聚类可以被视为粒计算中的粒子集,因为一个类别本质上是训练集中样本的集合。从这个角度来看,粒计算中的每个粒子与训练集的每个样本一一对应,粒子ui上的粒子集UN对应整个训练集,粒度(UN,∘)上的粒结构∘表示粗度UN上粒子之间的结构关系,2.2节已将其指定为一个代数二元算子∘(x,y),于是,代数粒模型可以定义如下:

定义1代数粒被定义为一个二元组(UN,∘N×N),其中:

UN={ui|i=1,…,N}

(1)

∘N×N={si,j←ui∘uj|ui,uj,si,j∈UN}

(2)

其中,粒集UN是N元有限集,粒结构∘N×N是UN上的代数二元算子。

定义1中的∘N×N的结果是二维矩阵,其描述任意2个粒子ui和uj之间的结构关系的二元映射函数,即ui∘uj→si,j。显然,定义1中的粒结构∘N×N是粒集UN上的一个代数运算,即对于粒集UN的任意2个粒子ui和uj,在封闭二元算子∘的运算下,当且仅当ui和uj映射到UN中的1个元素,即si,j∈UN。

表2给出了一个代数粒(UN,∘N×N)的例子,其中粒集UN={{a},{b},{c},{d},{e},{f},{g},{h}}处于问题最初始阶段(离散空间)的最细粒度,即UN中的每个元素都是一个粒子,粒结构∘N×N的结果是一个二维矩阵,表示UN中任意2个变量之间的二元代数运算,例如{a}∘{b}={a},{c}∘{g}={e}。若分别将粒子{a},{b},{c},{d},{e},{f},{g},{h}同态映射为0,1,2,3,4,5,6,7,则表2中的粒结构∘N×N是同余代数运算(x×y)%8,即x乘以y并除以8的余数,如表3所示。

3.2 基于代数粒的聚类方法

从粒计算的角度来看,聚类方法主要对应于粒化过程,其核心工作是将原始粒度聚类成更粗的粒度。在3.1节定义了代数粒之后,本节主要设计基于代数粒的聚类方法,即如何将代数粒(UN,∘N×N)进行粒化。因此,本节将针对以下2个问题进行讨论:

Table 2 Granule structure ∘N×N results表2 粒结构∘N×N的结果

Table 3 Granule structure ∘N×N resultsin homomorphic mapping of table 2表3 同态映射表2中的粒结构∘N×N的结果

Q1:如何对粒集UN进行粒化,即如何将粒集UN聚类为更粗的簇?

Q2:如何粒化粒结构∘N×N,即在对粒集UN进行聚类时,如何将粒结构∘N×N同态映射到更粗的粒度上?

为了求解问题Q1,在对粒集UN进行聚类时,需要一个粒化规则R。例如,在不考虑粒结构的情况下,容差邻域模型以相容关系进行粒化[4,5];粗糙集模型以等价关系进行粒化[6,7];商空间模型指定粒结构为拓扑序,并以等价关系进行粒化[8,9]。以表2中的代数粒(UN,∘N×N)为例,若基于相容关系,它可以被粒化为具有3个粒子{a,b,c,d},{c,d,e,f},{g,h}的覆盖,其中粒子{a,b,c,d}和{c,d,e,f}之间存在一个交集{c,d}。若基于等价关系,它们可以被粒化成1个等价划分{{a,c},{b,f},{d,h},{e,g}},它们之间没有交集,即互不相容。(UN,∘N×N)对问题Q1中的UN进行粒化时,至少需要一个等价关系,因为作为代数粒度,粒集UN是互斥的,它们之间没有交集。

在求解问题Q2过程中,当对粒度(UN,∘N×N)的代数结构进行聚类时,粒化不能由容差关系或等价关系决定,因为它与最初的二元代数算子∘N×N的粒结构有关。实际上,为了同态映射代数算子∘N×N到一个更粗的粒度上,粒化必须基于同余关系,也就是说,只有给定一个同余关系R,原粒结构∘N×N才会同态映射到聚类粒结构上。

基于以上分析,基于代数粒的粒度聚类方法可以定义如下:

i∈p-1(i′),j∈p-1(j′),i′,j′=1,2,…,M

(3)

i∈p-1(i′),j∈p-1(j′),i′,j′=1,2,…,M}

(4)

定义2描述了如何将原始粒度(UN,∘N×N)聚类成更粗粒度(UM,⊕M×M)。式(3)给出了聚类粒集UM的获取方法,即从原始粒集UN到聚类粒集UM的映射方法。式(4)给出了原始粒结构∘N×N构造聚类粒结构⊕M×M的方法。

定义2中式(3)是聚类粒集的获取方法,因为已知条件R是一个同余关系,它本质是根据自然映射p:UN→(UN/R)获取同余划分UN/R的过程。事实上,经典商空间模型和粗糙集理论根据等价关系R进行粒化,即其聚类粒集是一个等价划分UN/R;而容差邻域模型根据相容关系R进行粒化,即其聚类粒集是一个完全覆盖UN/R。事实上,多数文献对粗糙集理论和商空间模型的分析,都是直接给出等价关系的等价类,粗糙集理论主要讨论知识粗糙/近似表示和知识约简,商空间模型主要讨论知识粒化和粒度转换。

为简单起见,下文将新方法与商空间模型和容差邻域模型进行实例对比分析时,直接给出其粒化关系——同余关系、等价关系、相容关系的相应同余划分、等价划分、完全覆盖,如表4第3列所示。

图3展示了定义2中基于代数粒的聚类方法的主要步骤,对应粒计算理论中的粒化过程,即粒集粗化UN→UM和粒结构粗化∘N×N→⊕M×M。所以,定义2提供了一个基于代数粒的聚类新方法,并从粒结构的角度丰富了粒计算理论。

Figure 3 Clustering method of granules UN and granule structure ∘N×N图3 粒集UN和粒结构∘N×N的聚类方法

3.3 聚类方法实现

算法1描述了定义2中基于代数粒的聚类方法实现的伪代码。输入论域U={u1,u2,…,uN}上的最细粒度(UN,∘N×N)对应的原始粒集UN,原始粒结构∘N×N对应的二维矩阵AN×N,以及同余关系R的粒化规则;算法输出聚类粒集UM与聚类粒结构⊕M×M对应的二维矩阵BM×M。

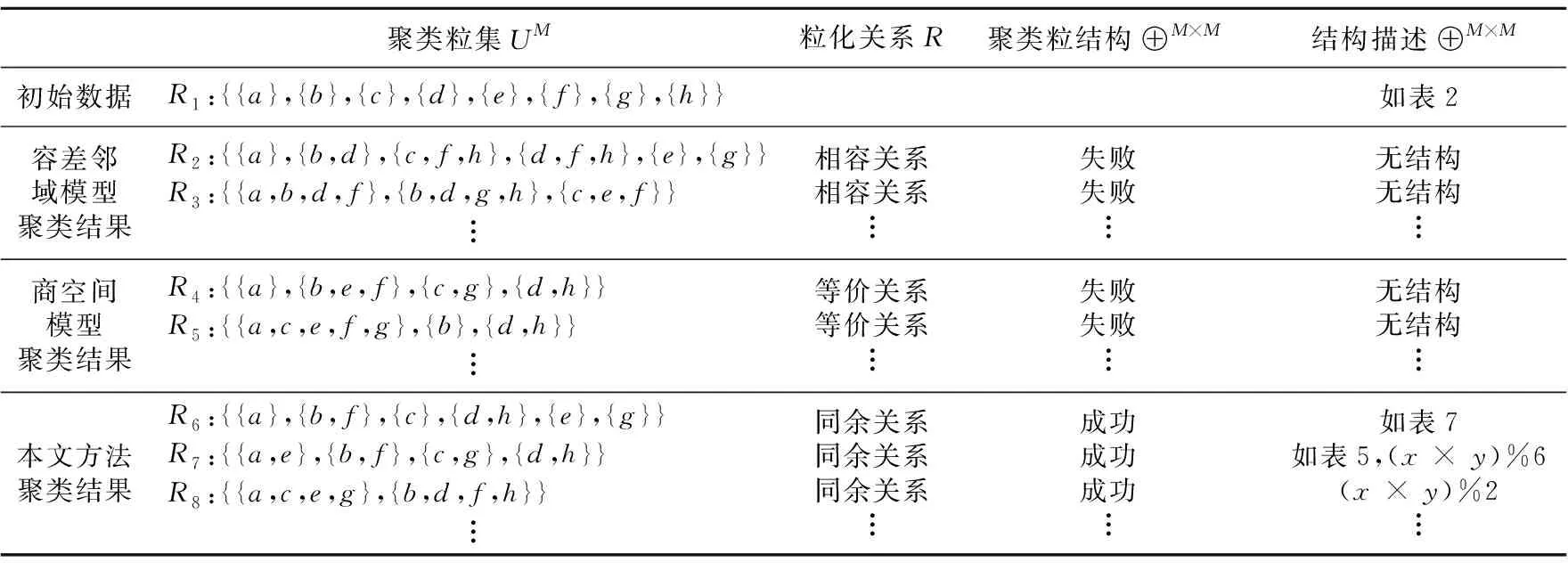
Table 4 Comparative results of several models to cluster algebraic granularity in table 2表4 几种模型对表2中代数粒进行聚类比较

算法1 对粒度(UN,N×N)进行聚类输入:初始粒集 UN={{u1},{u2},…,{uN}},粒结构N×N即AN×N,同余关系 R。输出:聚类粒集 UM,聚类粒结构⊕M×M。Step 1 由同余关系R获得同余划分UM=UN/R;Step 2 M=|UM/R|;Step 3.1 初始化 BM×M,即∀bi,j←∅;Step 3.2 for t1←1 to N doStep 3.3 for t2←1 to N doStep 3.4 获得 at1,t2 from AN×N;Step 3.5 for s1,s2←1 to M do Step 3.6 Search ut1∈us1的索引s1,where ut1∈UN,us1∈UM;Step 3.7 Search ut2∈us2的索引s2,where ut2∈UN,us2∈UM;Step 3.8 end forStep 3.9 bs1,s2←bs1,s2∪at1,t2;Step 3.10 end for Step 3.11 end for Step 4 输出聚类粒集 UM;Step 5 输出聚类粒结构⊕M×M,即BM×M

在算法1中,Step 1根据定义2中的已知条件——同余关系R直接获得聚类粒集UM,即同余划分UN/R。Step 3.1将粒结构⊕M×M的结果初始化为空矩阵,然后Step 3.2～Step 3.11建立聚类粒结构⊕M×M的矩阵BM×M,这是该聚类方法中最重要的步骤。根据式(4),∀x,y,有x∘y∈[x]⊕[y],其中[x]指粒子x的聚类粒集,即聚类前的任意2个粒子的运算结果一定属于这2个粒子的同余类的运算结果。于是,Step 3.2～Step 3.11中聚类粒结构⊕M×M的建立方法是,从聚类前的表2出发,Step 3.9逐步将表2中各粒子的运算结果(表2中每一项)归并到聚类后的表5中,其中Step 3.5～Step 3.8先检索表2中粒子所要归并入的表5中位置(下标)i′和j′。最后,Step 4和Step 5输出聚类粒集UM,以及聚类粒结构⊕M×M的结果即二维矩阵BM×M。

现在从时间复杂度分析聚类粒结构⊕M×M的生成矩阵BM×M。如果根据式(3),从聚类后的表5出发,逐个生成表5中元素bi,j,显然外循环的时间复杂度为O(M2),而每个元素bi,j根据[x]⊕[y]=[x∘y]生成,其时间复杂度为O(N2),所以,整个算法的时间复杂度为O(N2·M2)。显然,如果直接根据定义(2)进行聚类,其时间复杂性O(N2·M2)比较高。于是,本文采用启发式方法设计了效率更高的聚类算法 ,如算法1所示,时间复杂度由Step 3.2、Step 3.3和Step 3.5决定,整个算法的时间复杂度改进为O(N2·M)。

Table 5 Clustering the granule structure ∘N×N results in table 2表5 对表2的粒结构∘N×N的结果进行聚类

下面进一步举例说明算法1的实现过程。如表4所示,当通过同余关系R7对表2中的代数粒(UN,∘N×N)进行聚类时,Step 1获得聚类粒集UM={{a,e},{b,f},{c,g},{d,h}}。Step 3.1将聚类粒结构⊕M×M初始化为空矩阵,其中Step 2指定矩阵⊕M×M规模为M=|UN/R|。Step 3.2～Step 3.11根据定义2中式(4)将聚类粒结构⊕M×M推导为表5所示的矩阵BM×M,其同态映射矩阵如表6所示。显然,表6中聚类粒结构⊕M×M是一个代数运算(x×y)%4,即它是一个同余运算,其具体聚类过程如图4所示,图中U1～U4表示全论域U的子集。

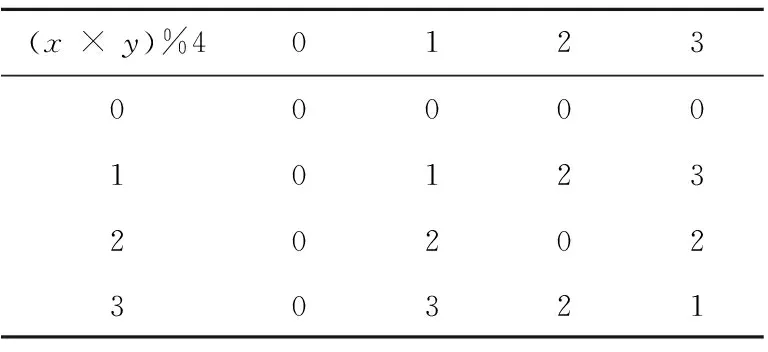
Table 6 Granule structure ⊕M×M results in homomorphic mapping of table 5表6 同态映射表5中的聚类结构⊕M×M的结果

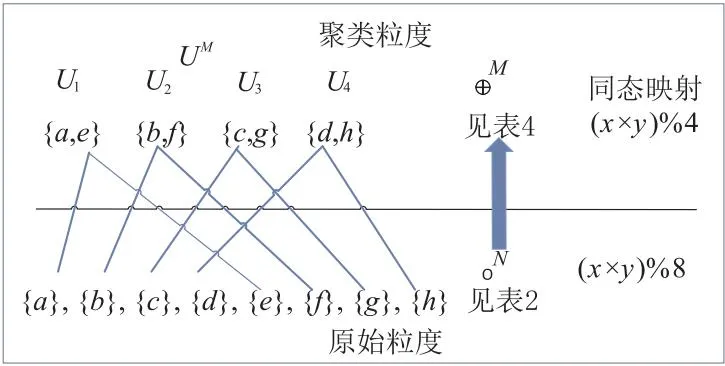
Figure 4 Clustering process of algebraic granularity (UN,∘N×N) in table 2图4 表2中代数粒(UN,∘N×N)的聚类过程

4 模型对比与分析

本节将提出的基于代数粒的聚类方法与传统粒计算聚类方法中的容差邻域模型和商空间模型进行对比实验,分析三者之间的差异性,得出结论:基于代数粒的聚类方法具有更好的结构完备性,且具有更好的有效性和鲁棒性。

表2描述了一个代数粒(UN,∘N×N),粒集为UN={{a},{b},{c},{d},{e},{f},{g},{h}},通过表3的同态映射可以清楚地看出,粒结构∘N×N是(x×y)%8的二元代数运算。下面以表2中的代数粒为例,通过基于代数粒的聚类方法、容差邻域模型和商空间模型分别对其进行聚类。

4.1 基于代数粒的聚类

定义1给出了代数粒的形式化描述(UN,∘N×N),定义2给出了代数粒的聚类方法,即基于同余关系R的粒集聚类UN→UM和粒结构聚类∘N×N→⊕M×M。

在基于代数粒的聚类方法中,3.3节已经通过算法分析了表2中代数粒的聚类过程,显然其粒结构由表3中的同余运算(x×y)%8聚类为表6中的同余运算(x×y)%4。

将表2中的代数粒(UN,∘N×N)按表4中同余关系R6进行聚类,其粒集UN由{{a},{b},{c},{d},{e},{f},{g},{h}}聚类为更粗粒集UM={{a},{b,f},{c},{d},{e},{g},{h}}。根据式(4),其粒结构∘N×N由表2聚类成表7。若将表7中的粒子{a},{b,f},{c},{d,h},{e},{g}分别同态映射为0,1,2,3,4,5,则表7中的聚类粒结构同态映射为表8。虽然表8中代数算子不表示为 (x×y)%6,但根据定义1中的代数粒定义,对于任何ui,uj∈UM,都存在ui∘uj∈UM,即表7和表8中的聚类粒结构仍然具有代数运算的封闭性,即表2中的原始粒结构仍被聚类为更粗的粒结构,表7和表8中的聚类粒结构仍然具备结构完备性。因此,本文所提出的基于代数粒的聚类方法仍然有效。

Table 7 Clustering the granule structure ⊕M×M in table 2 with congruence relation R6表7 用同余关系R6对表2的粒结构⊕M×M的结果进行聚类

Table 8 Granule structure ⊕M×M results in homomorphic mapping of table 7表8 同态映射表7中的聚类结构⊕M×M的结果

4.2 容差邻域模型聚类

在容差邻域模型中,不对粒结构进行讨论,粒集通过相容关系进行聚类。例如,在表2的代数粒(UN,∘N×N)中,如果按表4中的容差关系R2和R3进行聚类,则聚类粒集为覆盖{{a},{b,d},{c,f,h},{d,f,h},{e},{g}}和{{a,b,d,f},{b,d,g,h},{c,e,f}},但粒结构UN×N不能被聚类,如表4所示。

4.3 商空间模型聚类

在商空间模型中,粒结构被指定为拓扑结构,粒集通过等价关系进行聚类,而粒结构被聚类为商拓扑。因此,一个代数粒(UN,∘N×N)的粒集UN仍然可以利用商空间模型进行聚类,但代数算子的粒结构∘N×N不能被聚类。若仍然按照定义2中式(4)进行粒结构聚类,则聚类粒结构不再具有定义1中的结构完备性。

将表2中的代数粒(UN,∘N×N)按表4中等价关系R4进行聚类,其粒集UN由{{a},{b},{c},{d},{e},{f},{g},{h}}聚类为更粗粒集{{a},{b,e,f},{c,g},{d,h}}。若仍然根据定义2中式(4)对粒结构进行聚类,则粒结构∘N×N的结果将由表2聚类成表9。若将表2中的粒子{a},{b,e,f},{c,g},{d,h}分别同态映射为0,1,2,3,则表9中的聚类粒结构同态映射为表10,但显然表10中代数算子却不表示为(x×y)%4。

表9和表10的粗体项表示,聚类后的代数算子⊕M×M的粒结构不再与原代数算子∘N×N同构,即虽然粒集UN={{a},{b},{c},{d},{e},{f},{g},{h}}被成功聚类为UM={{a},{b,e,f},{c,g},{d,h}},但原始粒结构∘N×N未被聚类。因为根据定义1,代数粒结构必须具有代数运算封闭性,即具有结构完备性,但表9和表10中的聚类粒结构显然不具备结构完备性。例如,表10中b1,1={a,b,e,f}∉UM,但u1,1=u0∪u1= {a}∪{b,e,f},即通过等价关系R4进行聚类,则定义2中的聚类方法不再有效。

Table 9 Clustering the granule structure ⊕M×M resultsin table 2 with equivalence relation R4表9 用等价关系R4对表2的粒结构⊕M×M的结果进行聚类

Table 10 Granule structure ⊕M×M resultsin homomorphic mapping of table 9表10 同态映射表9中的聚类结构⊕M×M的结果

4.4 差异性分析

从上述基于代数粒的聚类方法、容差邻域模型和商空间模型对代数粒进行聚类的实验结果及其分析可以发现,它们之间的根本性区别在于:基于代数粒的聚类方法通过同余关系对粒集进行聚类,并通过定义2中式(4)对粒结构进行聚类;容差邻域模型通过相容关系对粒集进行聚类,且不考虑粒结构;商空间模型通过等价关系对粒集进行聚类,同时将粒结构聚类到拓扑商空间。

表面上,基于代数粒的聚类方法、容差邻域模型和商空间模型这三者之间似乎没有明显的相关性,但在数学上,同余关系Ra、等价关系Rb和容差关系Rc之间存在如下偏序关系Ra⊆Rb⊆Rc,从而有式(5)而立:

∀x,y∈UN,Ra(x,y)⟹Rb(x,y)⟹Rc(x,y)

(5)

上述偏序关系从本质上决定了粒集与粒结构的聚类方法,因此可以从表4中得出结论,若给定代数粒(UN,∘N×N)上的同余关系Ra,因为同余关系既是等价关系又是相容关系,则既可以基于代数粒的聚类方法来对粒集UN进行聚类,也可以用容差邻域模型和商空间模型来对粒集UN进行聚类。但是,如果给定同余关系Ra,代数算子的粒结构∘N×N只能使用基于代数粒的聚类方法进行粒结构聚类,详见表9和表10中的粗体项。这意味着,与容差邻域模型和商空间模型相比,基于代数粒的聚类方法在对粒结构进行聚类时,具有更好的结构完备性,且具有更好的有效性和鲁棒性,而这需要在更严格的同余关系的前提条件下进行。

5 结束语

本文从粒计算角度提出了一种新的基于代数粒的聚类方法。首先,基于代数二元算子,建立代数粒模型;其次,将粒度通过同余关系进行粒化,提出了基于代数粒的聚类方法,其中粒集被聚类为同余划分簇,粒结构被同态映射成更粗粒结构;然后,将新型聚类方法与容差邻域模型和商空间模型进行对比实验,结果表明,新型聚类方法具有更好的结构完备性和应用鲁棒性。

基于代数粒的聚类方法为代数结构的粒度聚类提供了一种新型方法,从结构上丰富了粒度计算理论,并为粒计算理论与机器学习的融合研究提供了理论依据。