一种油田配电网接入分布式电源的配置优化方法

2024-01-22章海静邵刚涛薛珍丽

西安石油大学学报（自然科学版） 2024年1期

章海静,杨庆,邵刚涛,薛珍丽,李攀

(1.国网陕西省电力有限公司电力科学研究院,陕西西安 710100; 2.中国能源建设集团西北城市建设有限公司,陕西西安 710038;3.长庆工程设计有限公司,陕西西安 710018; 4.陕西省油气井测控技术重点实验室,陕西西安 710065)

引言

油田配电网以抽油机为代表的感性负荷占到油区总负荷的80%以上,其功率因数较低。结构受地理条件限制,供电半径较长[1]。生产中,油气产量由上级政府计划决定,因生产引起的有功消耗无法减少,运行有其特殊性[2]。传统的无功优化方法可以减少配电网的功率损耗。文献[3]采用牛顿-拉夫逊一阶法和二阶法数学模型对地方电网进行了优化,取得了较好的结果。文献[4]将牛顿-拉夫逊法、约束条件与二次函数整合在一起进行无功优化,取得了较好的收敛速度与精度。文献[5]在传统的灵敏度分析选点的基础上做出改进,综合考虑网络结构和负载分布情况,利用各节点的灵敏度数值进行无功优化,取得了较好的收敛结果。文献[6]提出了基于负荷预测的多中心内点法的配电网动态无功优化,具有预测精度高、适应性强等特点。但随着全球温室效应的加重,发展清洁能源技术已成为低碳化背景下实现可持续发展的关键问题[7]。在当前“碳达峰、碳中和”要求下,油田配电网存在清洁替代率低、绿色低碳不达标的问题。因此,考虑分布式电源接入的优化配置问题已成为配电网的主流研究方向。

根据中石油《关于进一步做好油气生产清洁能源替代“十四五”规划的通知》,2025年新能源利用率将不低于25%,若碳排放得不到限制以及清洁替代率达不到标准,不但对企业造成巨大的经济损失,更有可能被迫停产或者受到处罚。在这种情况下,将光伏发电和井场燃气发电引入油田配电网,可以提高油田配电网清洁能源比例,满足配电网“碳达峰”的要求。

近年来,随着光伏发电等分布式电源的接入,研究人员对分布式电源的优化配置问题进行了大量的研究。文献[8]提出一种考虑抽油机负荷周期性波动的油田配电网损耗电量分析的改进方法,建立了低压侧并联固定电容器无功补偿的优化模型,采用随机抽样优化算法求解出电容器的最佳补偿个数和位置。文献[9]提出一种计及无功优化和多能协同交互的源-网-荷-储集中优化调度模型,可解决高比例可再生能源接入配网带来的无功问题。文献[10]通过建立多目标双层储能选址定容优化模型,降低系统运行成本并改善电压质量。文献[11]以网损最小、分布式电源成本最低和投资收益最高为决策变量,建立了有功无功协同优化模型。文献[12]充分考虑风光出力波动,在有功无功协同优化模型中考虑储能因素,通过储能充放电策略平滑风光出力波动,减少无功补偿装置的动作次数,以达到降低网络损耗、提升电网电压稳定性的目的。文献[13]的有功-无功协同优化方法重点对风场、光伏电站储能系统容量配置进行研究。文献[14]以运营商收益最大为目标,提出了一种配电系统中储能配置方法,促进了风电消纳。文献[15]基于随机规划方法提出一种考虑多类型分布式电源的电池储能定容选址模型。

从上述研究可以发现,已有的分布式电源多为风、光发电装置。而油田生产要求减少伴生气的直接排放,因此油田电网会因地质条件差异安装井口燃气发电机。由于可再生能源和小型燃气发电机的接入对油田配网并网点周围的电能质量和潮流分布将产生较大的影响,因此如何保证新能源接入后系统安全稳定、低碳经济运行,是目前油田电网亟待研究的课题[16]。

1 数学模型

1.1 接入分布式电源配置优化目标函数

油气产量不能随意减产,因此油田电网无功优化的目标是在保证油气产量的基础上,尽可能降低线路损耗,减少不必要的电费支出。碳中和的大背景下,在充分考虑新能源介入和油田伴生气发电特点的基础上,以优化后的网损和投资最小为目标,以保证网络中的电压、电流和功率处于安全运行允许范围内为约束,建立了油田配电网接入分布式电源配置优化数学模型,其目标函数为

minA=(FPLOSS+FS+FT+FC)。

(1)

式中:FPLOSS为有功功率网络损耗产生的费用,可表示为:

(2)

式中:α为电价,元/(kW·h);τ为年平均运行时间,h;PLOSS,i为流过线路i的有功网损;N为配电网的节点数。

FS为光伏发电投资和维护费用:

(3)

式中:k1为单位容量光伏发电装置年投资费用;f1为单位容量光伏发电装置年维护费用;NS为节点n处安装光伏发电装置的组数;S为单组光伏装置的容量;N为配电网的节点数。

FT是井口燃气轮机投资和维护费用:

(4)

式中:k2为单位容量井口燃气轮机年投资费用;f2为单位容量井口燃气轮机年维护费用;NT为节点n处安装燃气轮机的台数;T为单台燃气轮机的容量;N为配电网的节点数。

FC是补偿电容器的投资和维护费用:

(5)

式中:k3为单位容量补偿电容器年投资费用;f3为单位容量补偿电容器年维护费用;NC为节点n处安装电容器的组数;C为每一组电容器容量;N为配电网的节点数。

1.2 约束条件

(1)功率平衡约束

∑PG-∑PL-∑PLOSS=0,

(6)

∑QG-∑QL-∑QLOSS=0 。

(7)

式中:∑PG为有功出力总和;∑QG为无功出力总和;∑PL为负载消耗的有功功率;∑QL为负载消耗的无功功率;∑PLOSS为系统中有功损耗;∑QLOSS为系统中无功损耗。

(2)节点电压、支路电流约束

(8)

式中:Vn,φ为第n个节点的电压值;Vn,φ,min为节点电压最小值,取93%VN;Vn,φ,max为节点电压最大值,取107%VN;Ii,φ为第i条支路φ相电流值;Ii,φ,max为第i条支路过载电流的临界电流值。

(3)配电网进线功率约束

(9)

式中:P0为从进线流入配电网的有功功率;P0,min为从进线流入配电网的有功功率下限,取分布式电源参与发电时,根据以往运行情况该线路所连接的油田重要负荷的最小值;P0,max为从进线流入配电网的有功功率上限,取分布式电源不发电时,根据以往运行情况该线路出现的最大实际运行功率。

Q0为从进线流入配电网的无功功率;Q0,min为从进线流入配电网的无功功率下限,取进行无功补偿后,根据以往运行情况该线路出现的最小无功功率;Q0,max为从进线流入配电网的无功功率上限,取不采取无功补偿措施时,根据以往运行情况该线路出现的最大实际无功功率。

(4)光伏装置位置约束

油田生产现场地貌复杂,面积允许且太阳能辐照值达到4 500～5 600 MJ/(m2·a)的场地才适合安装光伏发电装置。用LS表示光伏装置是否适合在油田电网中的某节点位置安装:

(10)

(5)燃气轮机位置约束

燃气轮机不仅可以消耗掉由于超压而排空浪费掉的伴生气,而且形成的微电网也可以为周围采油作业提供环保的能源。用LT表示地质条件是否适合安装伴生气发电装置:

(11)

2 Hopfield神经网络

人工神经网络模型的基本组成单元为神经元模型,神经元模型是对生物神经元的工作方式的模拟[17]。Hopfield神经网络通过求解微分方程组确定规划问题的最优解,计算效率比随机搜索算法高[18]。HNN网络框架如图1所示。

图1 Hopfield网络框架

图中N1～Nn代表n个神经元,是输出单元,又是下一次计算的输入单元。X1～Xn为网络输入,y1～yn为网络输出。Vi(t)为网络在t时刻的状态,Wij为Ni到Nj的连接权值。n个节点之间的连接强度用n×n方阵W表示。通过对网络进行迭代训练和反馈运行,网络的能量函数值逐渐减少至稳态值,此刻对应的解即为网络方程的最优解。

3 优化配置的神经网络能量函数

为了确定补偿数量NT,NS和NC,必须对目标函数式(1)进行求解,该问题属于典型的组合优化问题。常规的数学手段难以完成,因此本文运用Hopfield神经网络进行求解,首先建立表示规划状态的关联矩阵,见表1。

表1 电网规划状态的关联矩阵V

表中,J为电容器组数上限,K为光伏最大组数上限,M为燃气轮机最大台数上限。其中,1～J列单元数值为1表示对应列的电容器给对应行的负荷节点提供补偿,每一列单元为1的个数不超过1,保证每组电容器不能重复补偿给多个负荷点。

J+1～J+K列,单元数值为1表示对应列的光伏发电容量为对应行的负荷节点进行发电。每一列为1的单元个数不超过1,保证对应列的光伏发电容量不能重复分配给多个节点进行发电。

J+K+1～J+K+M列,单元数值为1表示对应列的燃气轮机为对应行的负荷节点进行发电。每一列为1的单元个数不超过1,保证对应列的燃气轮机不能重复分配给多个节点进行发电。关联矩阵中每个单元用vij表示。

该油田电网实际使用的光伏发电装置是通过逆变器接入电网的,因此可将其视为PQ节点,但P值和Q值为负数。与目标函数对应的神经网络能量函数的表示式为

(12)

能量函数的第一项对应目标函数的分项式(2),保证因网损造成的损失电费最少;

能量函数的第二项保证关联矩阵V的每一列为1的单元个数不超过1,即每一个电容器组或燃气轮机等装置只有一个安装地点,防止出现同一装置多点安装的非法计算结果;

能量函数的第三项对应目标函数的分项式(5),保证补偿电容器投资及维护费用最少;

能量函数的第四项对应目标函数的分项式(3),保证光伏发电装置投资维护费用最少;

能量函数的第五项对应目标函数的分项式(4),保证燃气轮机投资及维护费用最少;

能量函数第一项、第三项、第四项和第五项之和对应了优化补偿目标函数的数学模型式(1),保证系统有功和无功费用最小;

第六项和第七项保证光伏发电和燃气轮机只能安装在地貌及地质条件许可的地方。

考虑到式(12)的Hopfield神经网络能量函数求解时会经常陷入无效解,文献[19]将动态方程变为:

(13)

其中,uij为神经元输入。由式(13)可得:

(14)

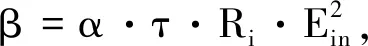
(1)电容器组数上限

(15)

式中:QΣ为由负荷统计确定的最小补偿无功上限;QC为单组电容器补偿的无功功率。

(2)光伏最大组数

(16)

(3)燃气轮机最大台数

(17)

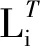
利用欧拉法求解式(14)即可得所求解。每次迭代计算后电压Ui会变化,可以利用潮流计算确定变化的Ui。在利用Hopfield神经网络获得最优解后,个别节点电压可能会不满足约束条件。因此,本文将Hopfield神经网络所得解作为初始值,利用如图2所示算法最终确定最优解。

图2 潮流约束计算流程

4 算例验证

某油田W变电站10 kV LD#线,线路长度24.97 km,共有35段线路,线路接带有10/0.4 kV配电变压器26台,总容量为2 919 kVA,功率因数0.62。线路单位长度的电阻为0.057 087 8 Ω/km,单位长度的电抗为0.367 217 Ω/km,单位长度电纳为0.000 003 3。线路的所有节点参数见表2。

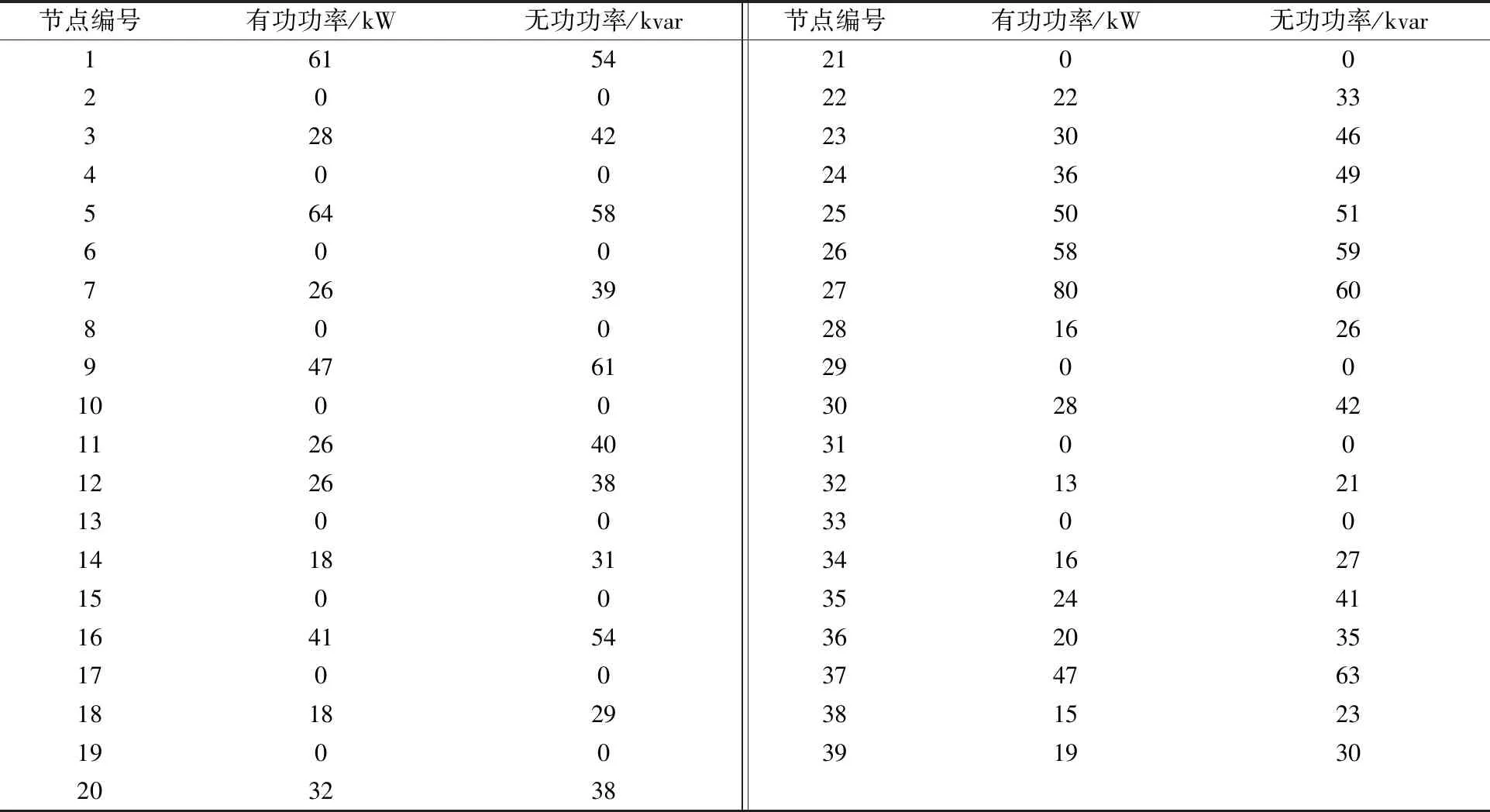
表2 10 kV LD# 线路节点参数

取贴现率为0.06,经济使用年限为20 a,则等年值系数为0.087 1。投资和维护费用系数取值:k1=420 元/kW,f1=10元/kW,k2=3 000元/kW,f2=75元/kW,k3=210元/kvar,f3=5元/kvar。年运行时间τ=7 000 h,电价α=0.4 元/(kW·h),E1≈10,E2≈200,E3≈5,E4≈5,E5≈5,E6≈300,E7≈300,循环计算500次,计算步长取0.01。按图2所示算法得出优化方案拓扑,如图3所示,图中红色部分为接入分布式电源进行优化配置后的功率补偿设备的安装位置及补偿容量。

图3 优化配置后配电网拓扑结构图

图3中节点22的变压器容量为80 kVA,所安装的燃气发电装机容量较大,为100 kW。结合该油田电网的实际地形图(图4)分析可知,节点22的位置正好处于采油区块末端,位于沟底,光照资源不足,但开采时伴生气资源非常丰富。该优化方案不但能够大幅减少伴生气的直接排放,而且可以弥补光照资源不足的劣势。油田电网接入分布式电源优化配置前后各项指标的统计见表3。

表3 优化配置前后各指标的对比

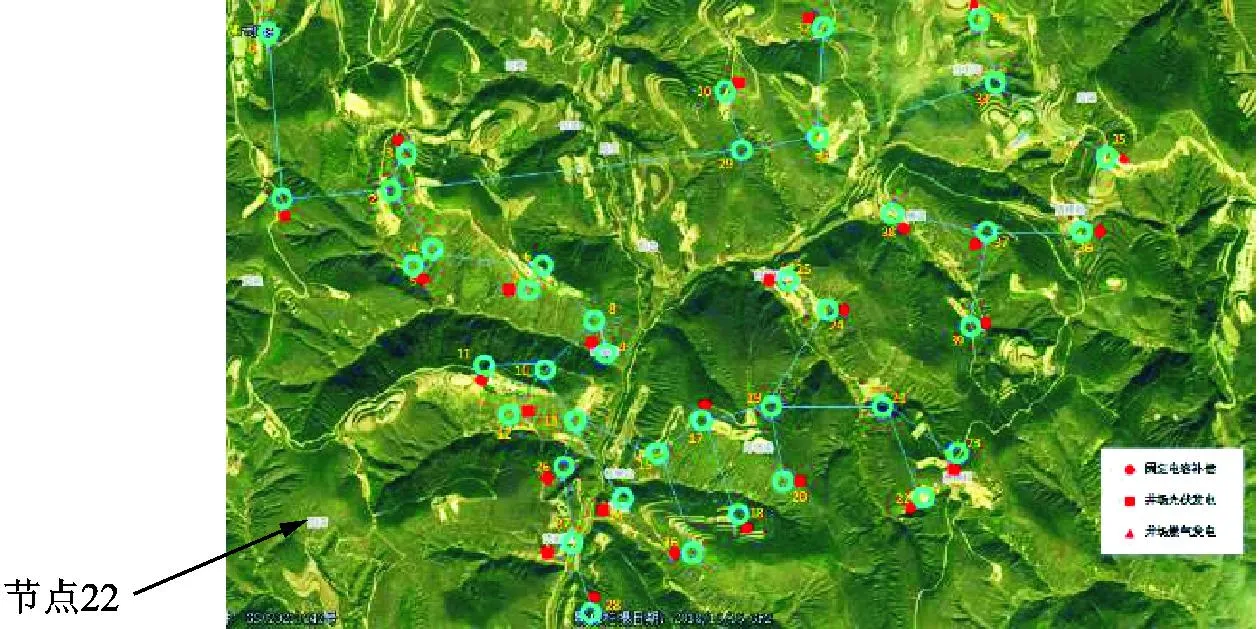
图4 配电网实际节点位置图

通过表3可以看出,所提算法可以保证油田电网在接入分布式电源进行优化配置后的功率因数满足供电要求,年供电成本相较于优化配置前的年供电成本节约150.24万元, 减少碳排放261 t/a,减少石油气排放227 500 m3/a。实现了部分清洁能源的替代,绿色低碳,清洁能源的替代率达到15.75%,满足油田公司对目前油田电网运行的节能环保要求。