球型防喷器胶芯安全性能与结构优化
2024-01-22黎文奇刘少胡牟易升易先中
刘 洋,黎文奇,管 锋,刘少胡 ,牟易升,易先中
(1.长江大学 机械工程学院,湖北 荆州 434023; 2.中国石油集团工程材料研究院有限公司,陕西 西安 710077)
引言
目前,油气资源的勘探开发逐渐向深部地层延伸,然而超深井面临的井控形势也愈加严峻[1-2],如果防喷器设计和制造达不到额定工作要求,将会造成井喷等安全事故[3-4]。其中,球型防喷器在使用过程中,球型胶芯会受到钻柱的挤压和磨损作用,导致其密封性能降低。对此,国内外专家学者对深井防喷器结构进行了相关研究[5-7],HU等[8-10]研究了旋转防喷器各种参数对其密封性能的影响,讨论了旋转防喷器密封结构的失效机理,并分析了井压、起下钻速度、摩擦系数等参数对密封结构接触应力的影响,最后通过静态和动态密封性能试验研究为减少胶芯的失效事故提供依据。徐大萍等[11]分析了球型防喷器胶芯失效原因,为胶芯的设计和使用提供现场数据。邓又铭等[12]针对国产球型胶芯密封性差和寿命低的问题,建立了球型胶芯的三维结构,分析了胶芯密封压力、活塞行程与接触压力的关系。姚尧等[13]根据气控环形防喷器胶芯密封问题,对胶芯在3个不同阶段的变形和密封进行了仿真研究,表明胶芯的变形量和接触压力存在一定的对应关系。隋旭东[14]考虑到环境因素对环形防喷器的影响,对环形防喷器结构进行了分解,根据单因素评价集分析得到环境因素对胶芯和液控油路产生的影响最大。付海龙[15]根据过油管防喷器工作原理,通过建立胶芯参数优化目标,完成了胶芯尺寸优化,获得最佳长径比。王冬雪等[16-17]为开发适用于深井井控的防喷器,利用PROE软件和有限元软件实现对高压防喷器参数优化设计,利于对胶芯或支撑筋结构进行实时修改,加快了复杂的胶芯结构研发进程。
上述研究结果为球型防喷器安全评价提供了一定的理论指导,部分研究针对常规球型防喷器进行了三维仿真计算,但是缺少相应的试验数据支撑,且缺少针对球型防喷器胶芯密封性能的安全评价结论。本文根据常规球型防喷器实际尺寸进行三维建模,完成胶芯材料拉伸和压缩试验,找到橡胶材料最优本构模型,最后将该模型运用到胶芯仿真分析中,并根据常规胶芯密封结构进行二次优化设计,对常规和优化的胶芯密封结构进行安全性能评价分析,以确定球型胶芯密封段最优倒角切削量。
1 球型防喷器结构及工作原理
球型防喷器主要由顶盖、壳体、挡泥环、活塞、胶芯等构成,如图1所示。在关井动作时,胶芯沿顶盖内腔自下而上,从外缘向中心移动,最后达到密封钻杆与胶芯的环形空间的目的。球型防喷器在封井过程中,胶芯受到活塞的过度挤压和钻柱的摩擦作用,因此,胶芯在使用过程中经常发生橡胶掉块和密封面过度磨损现象,如图2所示。
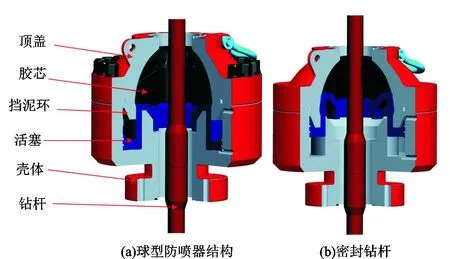
图1 球型防喷器及工作示意图

图2 胶芯失效案例
2 胶芯本构关系的建立及材料试验
2.1 胶芯材料非线性本构关系
橡胶作为一种典型的超弹性材料,它的本构关系非常复杂,现有文献对橡胶材料的模拟计算一般采用常用的本构关系模型[18-19],当不考虑橡胶材料的蠕变、Mullins效应及应力松弛等与时间相关的特点时,橡胶应变能函数可以近似表示为
W=W(I1,I2,I3)。
(1)
其中,
(2)
式中:I1,I2,I3为Green应变张量的3个不变量;λ1,λ2,λ3为3个主伸长率。
Rivlin从纯数学角度出发导出应变能密度函数的一般形式,即
(3)
式中:Cik为材料常数。
橡胶一般近似为不可压缩材料,因此I3=1,式(3)可简化为
(4)
作为应变能函数,Gregory认为Mooney-Rivlin模型没有考虑到足够的高阶项,故其预测的理论结果与试验所取得的数据有很大的差别[20],因此提出了三阶表达式
W=C10(I1-3)+C01(I2-3)+C20(I1-3)2+C11(I1-3)(I2-3)+C30(I1-3)3。
(5)

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3。
(6)
Mooney-Rivlin模型能够较好地反映橡胶在拉伸变形下的应力应变关系,却很难描述橡胶的压缩变形特征,而Yeoh 模型具有良好的大变形拟合能力,特别适合模拟填充橡胶。本文通过试验进一步对Yeoh模型和Mooney-Rivlin模型数据进行拟合,找到较优的本构模型数据,为完成球型胶芯的数值仿真计算提供试验数据。
2.2 胶芯材料应力应变关系试验
球型防喷器胶芯材料以丁腈橡胶为主,本节分别对胶芯材料进行单轴拉伸、单轴压缩、平面拉伸和体积压缩试验[21],如图3所示。通过对这4类试验数据的优化处理,得到胶芯材料的较优本构关系。

图3 胶芯材料试验
将2.1节的Yeoh 模型和Mooney-Rivlin模型作为本节拟合本构模型,采用 ABAQUS有限元软件对试验数据进行拟合评估,从而得出Yeoh 模型系数,拟合结果如图4所示。由图4可知,3种曲线在不同横坐标下应力应变值大小交替变化,当橡胶变形率超过200%以后,Yeoh 模型和Mooney-Rivlin模型的误差逐渐增加,Yeoh 模型相对于Mooney-Rivlin模型误差增量较小(图4(a)、(b))。当橡胶压缩变形率超过40%以后,Mooney-Rivlin模型的误差增加较大,如图4(c)所示。可见测试数据和拟合数据偏差较大,拟合结果不理想,但是总体趋势是相同的。当橡胶变形率超过 100%时,Mooney-Rivlin模型误差明显增加。从图4(d)所示曲线拟合程度来看,当橡胶体积压缩变形率在5%以内时,Yeoh 模型相对于Mooney-Rivlin模型能更好地反映丁腈橡胶的体积压缩本构模型。虽然超过该值后Yeoh 模型的误差会增加,但因橡胶材料泊松比较大,且试验所得橡胶的体积压缩量很小, 因此可假设橡胶为不可压缩材料,忽略橡胶体积的影响,所得的本构关系数据也较接近试验结果。

图4 四种试验数据拟合结果
针对上述4种拟合数据所得橡胶本构关系精度较低的问题,采用GB/T 7757方法和橡胶大变形不可压缩方法处理橡胶试验数据时[22],以丁腈橡胶的单轴压缩试验测试数据为基础,橡胶大变形不可压缩方法相对于GB/T 7757方法计算精度提高了约14%,如图5所示。由此说明采用橡胶大变形不可压缩方法处理试验数据所得到的本构关系精度有较大的提高。导入基于体积不可压缩大变形理论方式处理的应力应变数据,利用ABAQUS拟合得到Yeoh模型系数C10=1.109 MPa,C20=0.109 4 MPa,C30=0.333 2 MPa。运用该本构关系能够较准确地模拟丁腈橡胶的大变形行为。
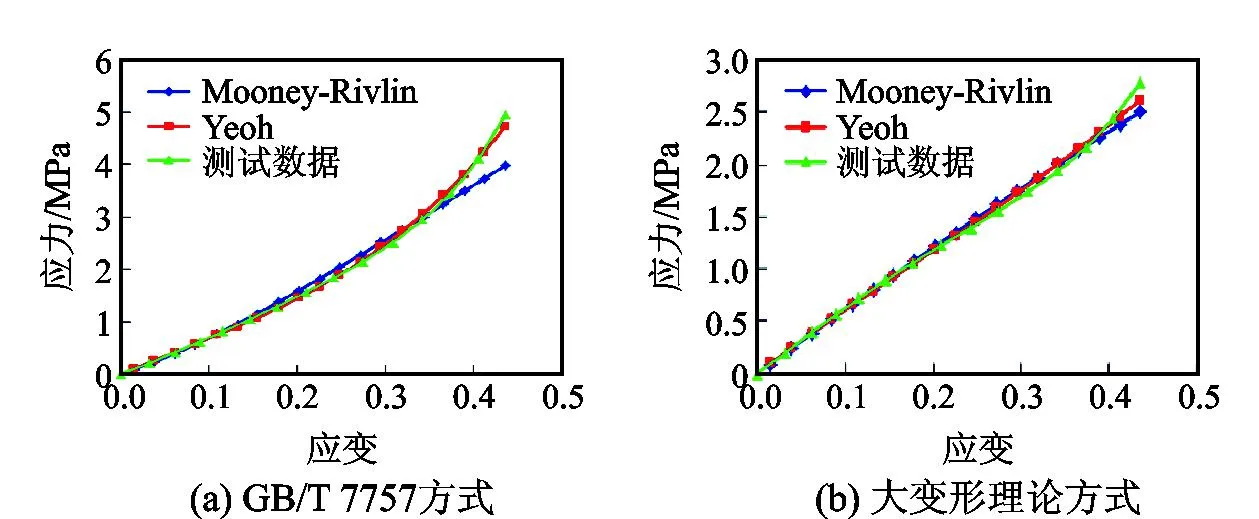
图5 两种处理方式数据拟合结果
3 常规胶芯密封结构有限元分析
以FH35-35 球型胶芯为研究对象,胶芯内部包含12块支撑筋,胶芯和支撑筋的外形结构如图6(a)所示。以第 2节分析结果为基础,球型防喷器胶芯材料的本构模型采用Yeoh本构模型,模型系数C10=1.109 0 MPa,C20= 0.109 4 MPa,C30=0.333 2 MPa。因为橡胶材料可被看作不可压缩超弹性材料,所以本次模型泊松比取0.5,其密度为1.5×10-9t/mm3。本次研究中,支撑筋等金属部件采用35CrMo材料属性,设定其杨氏模量E=210 GPa,泊松比μ=0.3,屈服强度为860 MPa,密度为7.8×10-9t/mm3。采用 ABAQUS/Explicit求解计算,分析过程中不考虑顶盖、支撑筋、活塞以及钻杆的变形,并指定各刚体部件的参考点为RP1、RP2、RP3,边界条件和载荷均施加在参考点上。考虑到在装配时,取活塞的极限行程为180 mm,符合实际情况。因此,在载荷步模块中,对活塞的参考点RP2施加沿Z轴正向的位移载荷180 mm,如图6(d)所示。

图6 球型胶芯结构及有限元分析模型
胶芯在不同时刻沿径向方向的位移云图如图7所示。从图7中可以看出, 胶芯向中心收缩的过程中,胶芯上部的橡胶沿径向方向的变形最大,向中心方向收缩最快,符合胶芯上部挤出橡胶多的特点。胶芯在不同时刻沿径向方向的位移云图如图7所示。从图7中可以看出,胶芯向中心收缩的过程中,胶芯上部的橡胶沿径向方向的变形最大,向中心方向收缩最快,符合胶芯上部挤出橡胶多的特点。如图7(c)所示,在第7 s时,胶芯上部的棱边最先开始与钻杆发生接触,此时胶芯沿径向方向的位移量为126.7 mm,该值的大小也在一定程度上反映了球型胶芯封井的速度。从图7(d)中可以看出,沿轴向正向,胶芯向中心方向挤出的橡胶逐渐减少,同时,在胶芯底部与活塞上表面接触的部位,由于活塞上表面的承载面积有限,胶芯底部的橡胶向中心挤出时有向下运动的趋势。
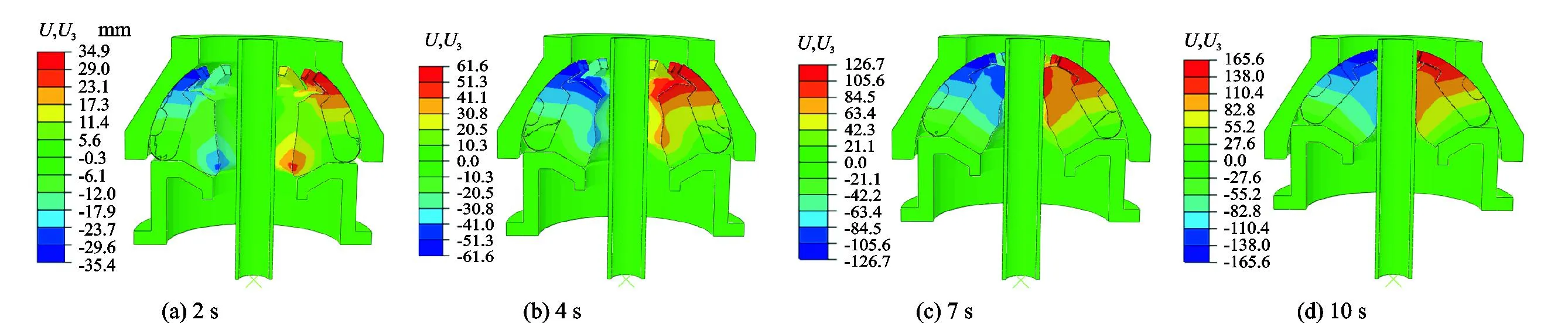
图7 不同时刻胶芯沿径向方向的位移云图
胶芯密封性能的好坏可以通过密封区域的接触压力和密封长度来衡量。图8为胶芯和钻杆的接触压力云图,接触压力最大值约为116.1 MPa。由于胶芯内壁表面产生褶皱,使胶芯沿环向方向的变形不一致,从而导致密封长度沿环向的差异较大,在产生褶皱的部位密封长度最短。从图8中可以看出,在钻杆表面,最大接触压力值发生在胶芯棱边与钻杆接触的区域,说明棱边的周围区域是胶芯密封钻杆的主要作用部位,并且产生褶皱的位置接触压力值较小。在产生褶皱的位置选取棱边与钻杆接触区域的一系列节点,根据节点上的接触压力值绘制成密封压力变化曲线,如图9所示。从图9中可以看出,接触压力值在60~90 MPa之间,极小值位于胶芯内壁表面产生褶皱的位置。因此,从密封长度和密封压力来看,胶芯在褶皱处的密封效果不理想,当流体压力较大时,可能发生流体泄漏或其他危险。

图8 不同时刻接触压力云图

图9 径向和轴向接触压力曲线
4 胶芯结构改进方案
4.1 球型胶芯结构改进设计及计算
根据第3节的分析结果可知,常规的球型胶芯在密封钻杆时,胶芯上部的变形量较大,胶芯在褶皱处的密封性能降低,这是导致该部位橡胶破坏的主要原因。同时,胶芯向上倾斜部位的变形较大,该位置容易造成应力过大而失效。从以上方面考虑,对胶芯的结构进行改进,改进胶芯向上倾斜部位,使胶芯上部呈现斜向下的倒角结构(图10(a)),并对新型胶芯结构进行数值模拟计算。由图10可以看出,胶芯向中心收缩的过程中,上部表面的橡胶沿径向方向的位移量基本一致。如图10(d)所示,在第 7 s时,胶芯上部的棱边最先开始和钻杆接触,此时胶芯沿径向方向的位移量为117.0 mm,和改进前的位移量(126.7 mm)相比降低了9.7 mm,说明新型胶芯上部橡胶减少了,但是胶芯对钻杆的密封速度(即封井速度)没有下降。

图10 改进后的胶芯结构及不同时刻径向方向的位移云图
从图10(e)可以看出,在分析完成时,胶芯上部仍存在一定的空间,即胶芯上部的橡胶与支撑筋没有发生接触。结果表明,当胶芯中心部位的橡胶受到井压作用时,在挤压变形过程中仍有运动的空间,能够有效避免胶芯上部的橡胶向上挤出而发生外翻造成应力集中。
4.2 改进后胶芯的密封性能
图11为改进后胶芯和钻杆的接触压力云图。从图 11可以看出,胶芯接触压力最大值约为200 MPa,平均接触压力约为40~100 MPa,通过测量,密封长度基本处于80~110 mm之间,且在褶皱位置密封长度有最小值。但是和改进前相比,最短密封长度由120 mm提高至150 mm,因此,有利于增强胶芯的密封性能。

图11 改进后胶芯的密封性能
为了进一步研究改进后胶芯密封压力值的分布情况,以钻杆为研究对象,选取如图12所示的路径,查询节点上的接触压力值,并和改进前曲线(图9)相比较。改进后曲线的峰值压力为 180 MPa,该峰值压力位于棱边对应的钻杆表面,和改进前的峰值压力120 MPa相比增大了60 MPa,且胶芯的有效密封长度更长,由改进前的约 80 mm提升至约120 mm,说明改进后的胶芯有助于提高褶皱处的密封性能。图 12(a)所示径向方向接触压力值在60~140 MPa之间变化,约为井口压力35 MPa的1.5~4.0倍,足以封闭井口流体。

图12 改进后胶芯密封性能曲线
4.3 胶芯结构尺寸优选
以上研究表明,胶芯上部橡胶的储量对胶芯的密封性能和应力值影响不同,因此,需要进一步对胶芯上部的结构尺寸进行优选。具体优选方法:在新型胶芯结构的基础上,改变胶芯上部的倒角部位切削量, 如图13(a)图所示。切削深度d分别为-5、0、5、10 mm,即在新型胶芯结构的基础上,分别对倒角部位加厚5 mm,削去 0、5和 10 mm,并分析这4种胶芯密封性能的变化规律,找到最优的倒角结构。
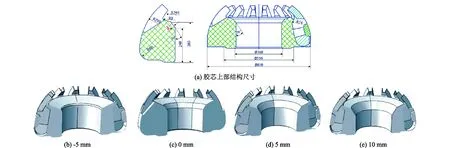
图13 胶芯结构尺寸优选示意图
图14为不同切削尺寸胶芯的等效应力云图。从图14可以看出,不同切削尺寸胶芯内壁表面的变形形态和应力分布情况也不同。在图14(a)中,对胶芯上部加厚5 mm时,胶芯内壁表面没有产生褶皱,但是内壁表面的应力值整体较高,明显高于其他 3 种情况;而在图14(b)、(c)和(d)中,胶芯内壁表面均产生明显褶皱,且应力的分布情况基本相似。

图14 胶芯 Mises 应力云图
根据前面的分析可知,胶芯上部圆弧根部位置应力值较高,最容易发生破坏,因此取该位置沿环向的6个节点,求出其应力平均值作为评价该部位应力水平的依据,如图15所示。由图15可知,胶芯上部加厚5 mm时,其圆弧根部的应力值明显增加,达到约55 MPa,说明该方法不可行。同时发现,切削加厚10 mm时胶芯上部圆弧根部应力值在4个值中最小,约为30 MPa,对应力值进行分析对比发现,加厚5 mm的胶芯结构已达最优。图16(a)-(d)为不同情况下钻杆的接触压力云图。
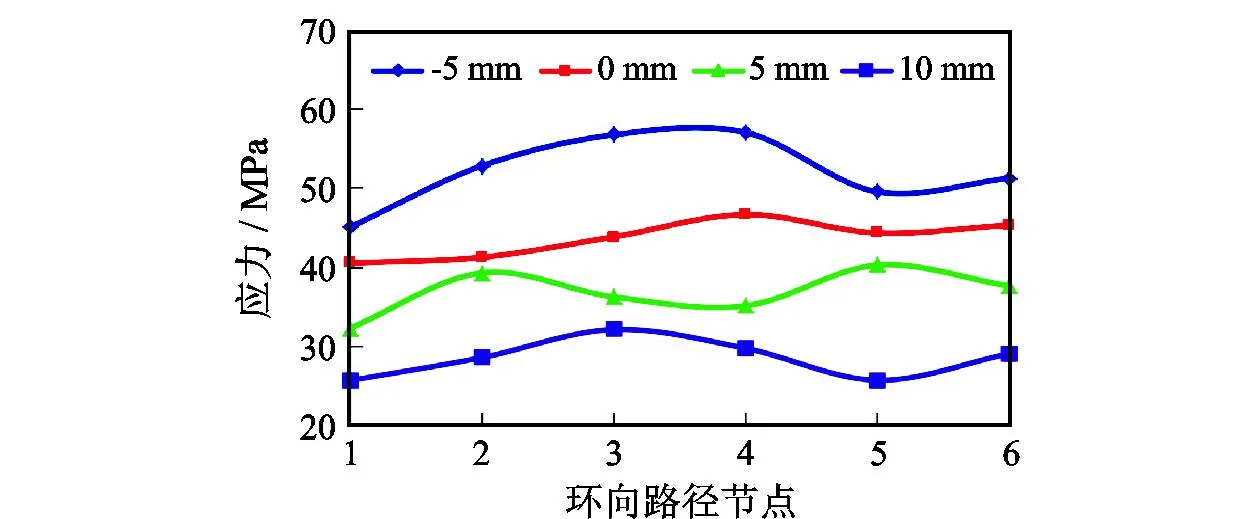
图15 环向节点应力曲线
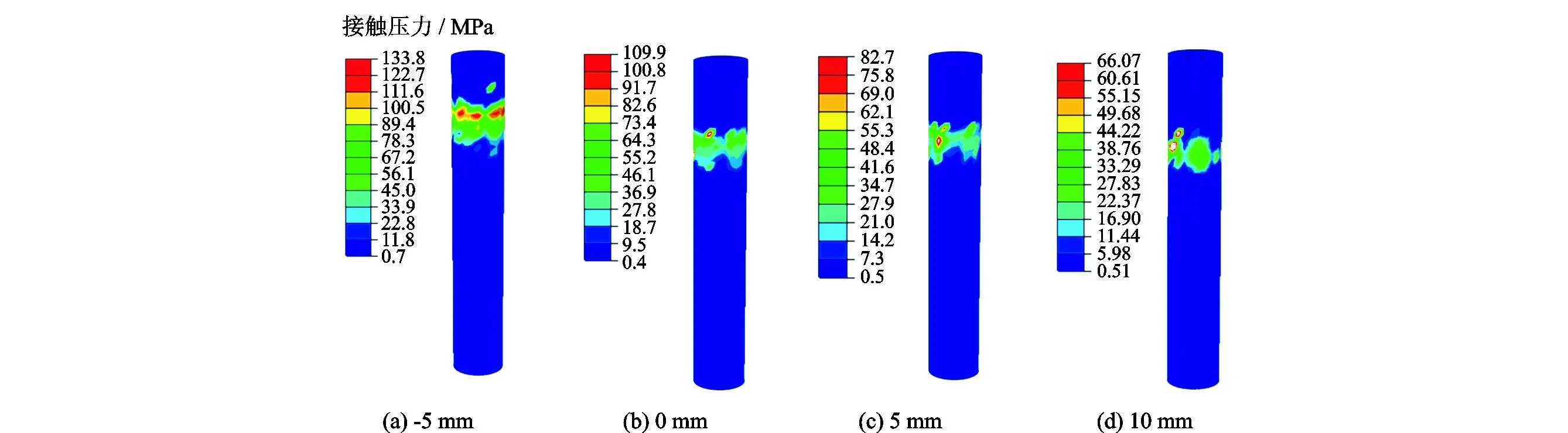
图16 钻杆的接触压力云图
在钻杆表面密封长度较短的区域,选择沿Z轴正向的一系列节点,得到密封压力沿轴向方向变化的规律,如图17所示。对胶芯上部切削5 mm和0 mm时,由于胶芯上部橡胶减少过多,导致胶芯的密封压力较低,密封长度较短,因此密封效果不理想。对胶芯上部加厚5 mm时,峰值密封压力提升至120 MPa左右,但是沿轴向方向的密封长度仍然较短,可能导致密封不可靠。而优选前的胶芯,其峰值密封压力约为90 MPa,相比优选前的胶芯,虽然峰值密封压力有所下降,但是总的密封长度明显更长,对提高胶芯的密封性能更有效。因此,综合考虑胶芯上部应力值的大小和密封性能的好坏,优选前的胶芯具备良好密封性能,并且胶芯上部应力值较低,有助于提高胶芯的使用寿命。
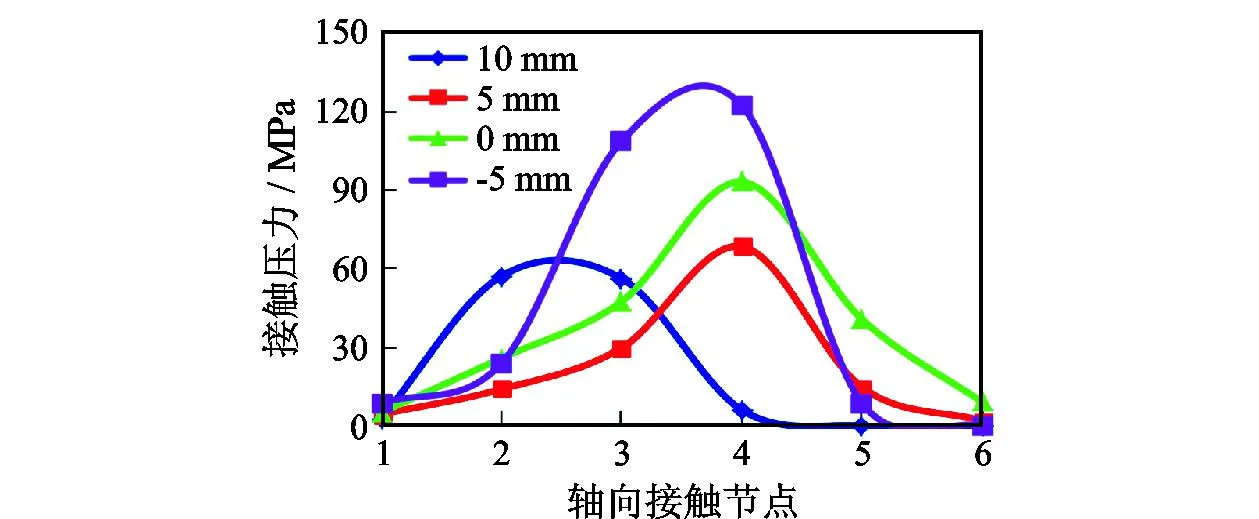
图17 密封压力沿轴向方向变化规律
优化前后胶芯倒角节点的应力和最大主应力曲线,如图18所示。对比可得,在-5 mm切削厚度情况下,整个倒角面各点应力值均较大,皆在55 MPa左右;其余3种倒角切削量的应力分布较相似,在支撑筋正对处的橡胶出现较大峰值,但随着切削量的加大,应力峰值减小,说明胶芯密封段切削量越大,橡胶所受的最大应力越小,胶芯强度越高。

图18 优化后胶芯倒角环形节点应力及最大主应力曲线
优化后胶芯倒角环形节点位移曲线如图19所示。从图19中可以看出,随着胶芯倒角切削量变大,同一位置胶芯轴向和径向变形量逐渐减小,胶芯倒角切削-5 mm和0 mm时其位移量较大。胶芯倒角位置的总位移和轴向位移变化趋势相似,而径向位移类似于正弦曲线变化,说明胶芯倒角位置位移变化呈现负对称变化。分析图18、图19可得,胶芯应力值随着胶芯倒角的增大而逐渐变小,所以容易造成胶芯储胶量不足,封井效果下降。为了避免胶芯倒角处橡胶脱离及开裂、胶芯底部橡胶开裂等明显的失效形式,并且要保证球型胶芯有良好的封井性能,这就要求球型胶芯有足够的储胶量,所以对胶芯密封段的倒角不宜过大。综合考虑应力、变形和密封性能,确定将球型胶芯密封段倒角切削量+5 mm作为胶芯橡胶部分优化后结构尺寸。
5 结 论
(1)胶芯向中心收缩的过程中,胶芯上部的橡胶沿径向方向的变形最大,向中心方向收缩最快,符合胶芯上部挤出橡胶多的特点。沿轴向正向,胶芯向中心方向挤出的橡胶逐渐减少,由于胶芯内壁表面产生褶皱,使胶芯的变形沿环向不一致,从而导致密封长度沿环向的差异较大。
(2)最大接触压力值发生在胶芯棱边与钻杆接触的区域,说明棱边的周围区域是胶芯密封钻杆的主要作用部位,并且在产生褶皱的位置接触压力值较小。
(3)改进后的胶芯与钻杆的接触压力最大值约为200 MPa,平均接触压力约为40~100 MPa,密封长度基本处于 80~110 mm之间,且在褶皱位置密封长度有最小值。但是和改进前相比,最短密封长度由120 mm提高至150 mm,因此,有利于增强胶芯的密封性能。
(4)在-5 mm切削厚度下,整个倒角面各点应力值均较大,其余3种倒角切削量的应力分布较相似,在支撑筋正对处的橡胶出现较大峰值,但随着切削量的增大,应力峰值减小,说明胶芯密封段切削量越大,橡胶所受的最大应力越小,胶芯越不容易被破坏,所以确定切削量+5 mm为胶芯倒角部位最优结构尺寸。
