海上浮式风机重力安装式筒形锚承载特性分析

康思伟，栾辰宇，张雨蓉，李飒

（1.中海油融风能源有限公司，上海 200120；2.天津大学建工学院，天津 300072）

0 引言

随着我国海上风电的迅速发展，有关海上风电技术的研究越来越受到工程界和学术界的重视[1]。浮式风机是一种安装在浮动结构上的海上风力发电装置。浮式风电场具有以下优势：可以进一步增加海上风力开发的范围和深度；可以解决近海用海矛盾突出的问题；对海床扰动小，较少干涉人类活动；为近海与航运通道提供更多空间；可为海上石油和天然气设施提供绿色电力[2]。浮式风机现有锚型主要有重力锚、打入桩锚、拖曳埋置锚、吸力桩锚、动力贯入锚与平板锚[3]。吸力桩锚、重力锚以及拖曳埋置锚已经被应用于海上浮式风电的建设中[4，5]。

吸力锚是一种常用的锚固基础型式，常用于承受倾斜荷载的条件。Aubeny C P[6]对吸力锚受倾斜荷载作用下的承载力进行了研究，提出了一种计算倾斜荷载条件下吸力锚承载力的简化上限解。Magued Iskander[7]对吸力锚在粘土和砂土中的特性进行了对比分析，指出在砂土中安装吸力锚时，容易出现超土塞现象，且吸力安装有可能导致其承载力的降低。目前，吸力锚更多地被应用于粘性土当中[8，9]。针对浮式风机的受力特征，Laszlo Arany[10]提出了作为浮式风机锚固基础的吸力锚的设计计算流程，指出了由于浮式风机受力特征与一般海洋结构物不同，设计荷载的准确对于吸力锚的设计至关重要，其在粘土中的设计计算方法可参考海洋工程中吸力锚的设计方法。

拖曳锚也是浮式风机锚固基础的一种选择，拖曳锚的精确定位是拖曳锚研究中的关键问题。毋晓妮[11]研究了黏土中浅埋拖曳锚的运动性能，并指出在埋深较浅的情况下，埋深比和方位角对土体中的屈服面均有影响。张春会[12]基于增量迭代法提出了预测拖曳锚嵌入运动轨迹和系泊点拉力的模型。但由于拖曳锚不能承受垂直荷载且需要相当长的拖曳距离，从而导致更大的现场调查成本，并增加了干扰现有系泊线和海底管道的可能性[13，14]。

重力锚的适用范围广，施工简单。重力锚主要用于海底管道的管汇系统，也被称为防沉板。针对重力锚，Gourvence S[15]提出了考虑H-V-M效应的重力锚破坏包络面方程。

重力锚也被用于海管铺设的起始锚，李飒[16]探讨了这类重力锚在复合荷载作用下的承载机理。这种重力锚由于其功能所限，重量一般都在十几到几十吨的量级。由于重力锚主要靠重力提供承载力，与其他锚固形式相比，其水平承载效率较低[17]。还有一些重量大的重力锚，主要被用于固定近海的海上结构物。

我国海域地质条件非常复杂，常常出现砂土或硬粘土地质。为此，本文以我国南海某海域粗砂地质为背景，考虑到粗砂渗透性较大，无法采用吸力安装，因此提出了采用重力安装方式的重力安装式筒形锚，该锚型可以提供近2 000 t的承载力，可用于粗砂等渗透性较大的风电场地，并利用数值分析对其贯入过程以及承载特性进行分析。

1 工程背景及锚固基础型式

南海某海域海底5 m深范围内均为粗砂，粗砂的基本物理力学性质见表1，海域的海况条件见表2。

表1 土层物理力学性质Table 1 The physical and mechanical properties of soil

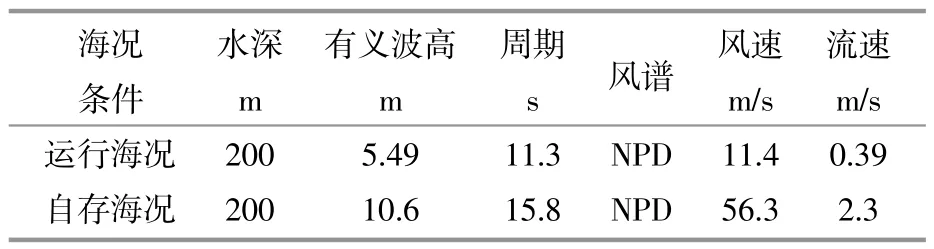
表2 南海某海域环境参数Table 2 Environmental parameters of a certain area in the South China Sea

本文采用半潜式浮式风机结构计算锚固基础的所受荷载，其中，浮式平台塔架浮筒上的稳态风量的表达式为

式中：Fw为风载荷推力，N；Cw为系数，一般取0.615 N・s2/m4；Cs为风力形状系数；Ch为风力高度系数；A为暴露在风中的塔架表面的垂直投影面积，m2。

采用NPD阵风谱来表示某处的时变风力，其表达式为

式中：SNPD（f）为NPD风谱的谱密度，m2/s；z为海平面的垂直高度，m；fw为风速频率；U10为海洋静水面以上高10 m处的10 min内平均风速，m/s。

采用Morison公式计算波浪荷载。

对单位波浪载荷积分得到总的波浪力为

式中：Fw（t）为某时刻浮式平台所受波浪荷载；ρw为流体的密度，kg/m3；CD为拖曳阻力系数；Dp为浮式平台结构的截面尺寸，m；u（z，t）为某时刻垂向分布浮式平台结构截面的水质点速度，m/s；Cm为惯性力系数；Ap为浮式平台结构的截面波浪方向的正投影面积，m2；a（z，t）为某时刻垂向分布浮式平台结构截面的水质点加速度，m/s2；B为浮式平台水下部分吃水长度，m；η为海平面标高，m；S为海域水深，m；z为海平面的垂直高度，z=0即为静水面，m。

海流荷载的计算式为

式中：FC为作用于浮式平台的海流力；Ad为浮式平台静水面以下部分迎流方向的投影面积，m2；vc为海流的流速，m/s。

根据环境载荷以及上述计算式，得到浮式风机锚固基础在运行海况条件下的水平荷载为11.2 MN，在自存工况条件下的水平荷载为14.4 MN。如果考虑安全系数为1.5，则其锚固基础需要提供约22 MN（2 200 t）的水平承载力。由于粗砂的密封性差，采用吸力锚安装风险较大，因此采用了重力安装式筒形锚。为了进一步说明重力安装式筒形锚的承载特性，本文同时对常规重力锚进行了计算分析。

重力安装式筒形锚[图1（a）]的重力块采用混凝土制成，尺寸为15 m×15 m×6 m。重力块下的筒形基础高度为4 m，壁厚0.05 m，重量约94 t，整体重量3 200 t左右。常规方形重力锚采用混凝土制成[图1（b）]，尺寸为15 m×15 m×6 m，干重约3 100 t。

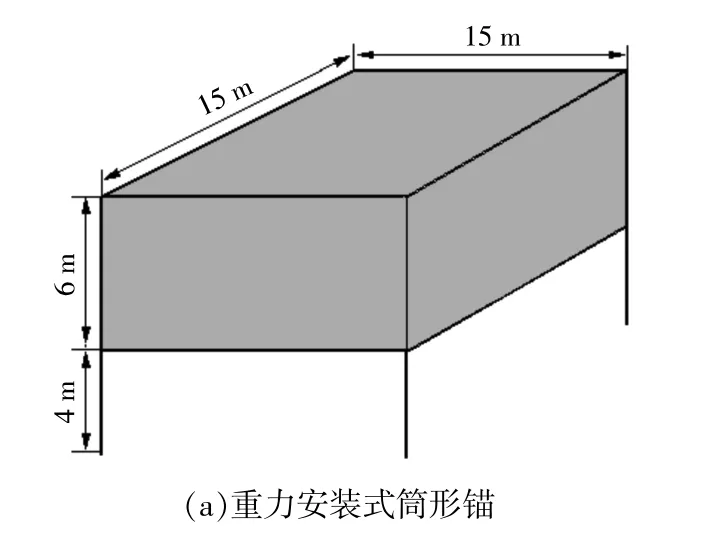
图1 两种锚型Fig.1 Two kinds of anchor

2 重力安装式筒形锚的贯入

重力安装式筒形锚需要通过筒形基础的贯入来提高锚固基础的水平承载力，因此能否贯入至设计深度是这种锚固基础能否成功使用的关键。在岩土工程中的下沉贯入属于大变形问题。对于大变形问题，目前的有限元模拟方法主要有任意拉格朗日-欧拉法（ALE）[18]、网格重划分和插值技术法（RITSS）[19]，耦合欧拉-拉格朗日法（CEL）[20]。其中RITSS实质上还是ALE法，它主要是将全自动网格重划分和现行插值技术与小变形计算相结合，以此避免大变形所造成的网格畸变。此外，还有学者采用了流体动力学法（CFD）[21]以及离散元法（DEM）[22]进行贯入模拟。

由于CEL方法结合了拉格朗日法与欧拉法的优点，利用了欧拉法中材料可以在网格里自由流动而网格保持固定位置这一特征建立模型，该模型可以有效解决大变形问题。因此，本文计算采用了CEL方法，通过有限元程序ABAQUS/Explicit模块实现。其中锚采用拉格朗日体，地基采用欧拉体。考虑到贯入工况的对称性，计算模型（图2）取实际模型的1/4。

图2 贯入的计算模型Fig.2 Penetration model

计算中将锚视为刚体，其单元类型为8节点三维体单元，单元默认划分尺寸为0.2 m。地基的计算深度为15 m，长度和宽度均为50 m。为了允许锚贯入过程中土体向上隆起，建立模型时在地基表面向上取2 m为计算模型的一部分，该部分区域初始材料设置为空。在贯入过程中，地基土会发生大变形，因此土体采用8节点三维欧拉体单元，本构关系采用M-C模型，模型参数取值见表1。

锚的总重为其实际水下重量，通过施加重力加速度的方法实现。地基底部3个方向上的速度设为0，对称面上法向速度为0，其他3个侧面3个方向速度为0。锚的对称面法向位移固定，其他位置可以自由移动。锚和地基之间设置接触面单元。法向接触为硬接触，由于地基贯入深度范围内的土体全部为砂土，切向摩擦系数取为0.4。

计算得到锚的贯入速度变化曲线如图3所示。

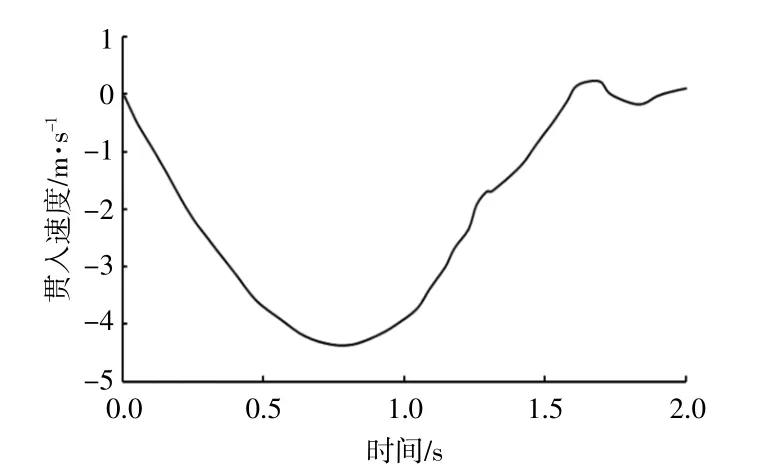
图3 锚的贯入速度随时间的变化关系Fig.3 The relationship between penetration velocity and time

计算得到锚的贯入深度随时间的变化过程如图4所示。由图4可知，锚的最终贯入深度为4.2 m，说明重力块可以保证筒形基础贯入至设计深度4 m。

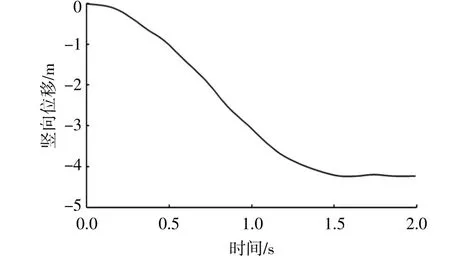
图4 锚的贯入深度随时间的变化关系Fig.4 The relationship between penetration depth and time

根据锚的贯入速度可以将锚的贯入过程分为两个阶段。第一阶段是贯入速度增加的过程，该过程持续到0.88 s时速度达到最大值，此时对应的贯入深度约为2.2 m。表明在此深度范围内，锚受到的贯入阻力小于锚的自重，锚为加速运动。第二阶段锚的贯入速度开始降低，直至降低为0，贯入过程停止。这表明第二阶段锚受到的阻力大于锚的重力，锚开始做减速运动，直至贯入停止。

3 不同锚固基础的承载特性

在保证重力安装式筒形锚可以贯入至设计深度后，进一步分析锚固基础的承载特性。锚固基础的承载力可采用小变形方法进行计算。本文采用拉格朗日有限元法，利用ABAQUS进行计算。计算针对重力安装式筒形锚和常规重力锚展开。重新建立有限元模型，由于采用拉格朗日有限元法计算，锚体和土体的单元类型均为8节点三维体单元。考虑到承载条件下的受力情况的对称性，为节省计算时间，采用了半模进行分析。地基的计算深度为15 m，长度为100 m，宽度为50 m，以上模型尺寸可以消除边界的影响。地基土采用M-C模型，为反映筒形基础和土的相互作用，在土-筒表面采用摩尔库仑罚函数的形式。采用位移加载法施加水平荷载，系泊点（荷载作用点）在重力锚上底面中心位置。

图5（a）为常规重力锚土体中塑性区的分布。由图中可以看到，在水平力的作用下，常规重力锚塑性区主要出现在重力锚底部的有限范围，依靠重力锚底部与土体的摩擦提供抗滑力。图5（b）为重力安装式筒形锚的土体中塑性区的分布。为清楚起见，给出三维图。从地基破坏时的塑性变形图可以看出，地基的破坏形式为典型的浅层破坏，筒体范围内的土体已全部被破坏。

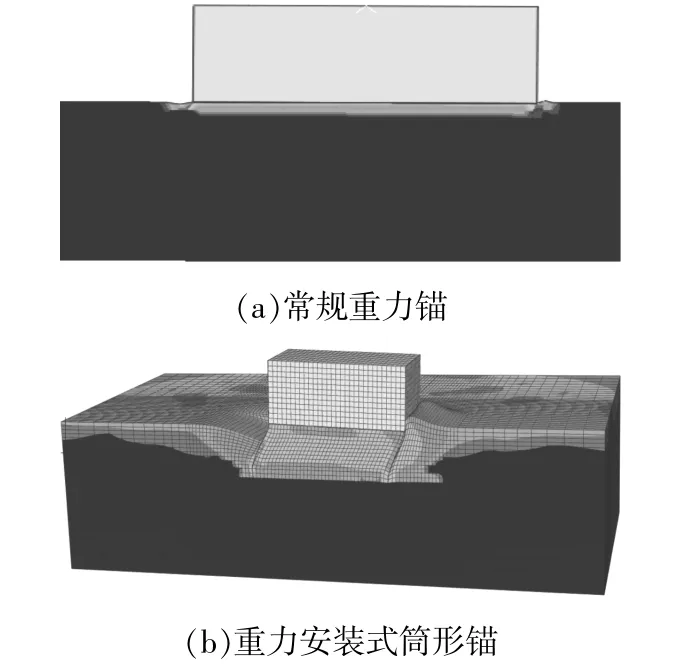
图5 水平荷载下地基破坏时的塑性区Fig.5 The plastic zone under horizontal loading

除此之外，本文还对两种不同类型的基础形式进行了竖向抗拔承载力的计算。图6为常规重力锚和重力安装式筒形锚在承受上拔力时土体中的塑性区分布。

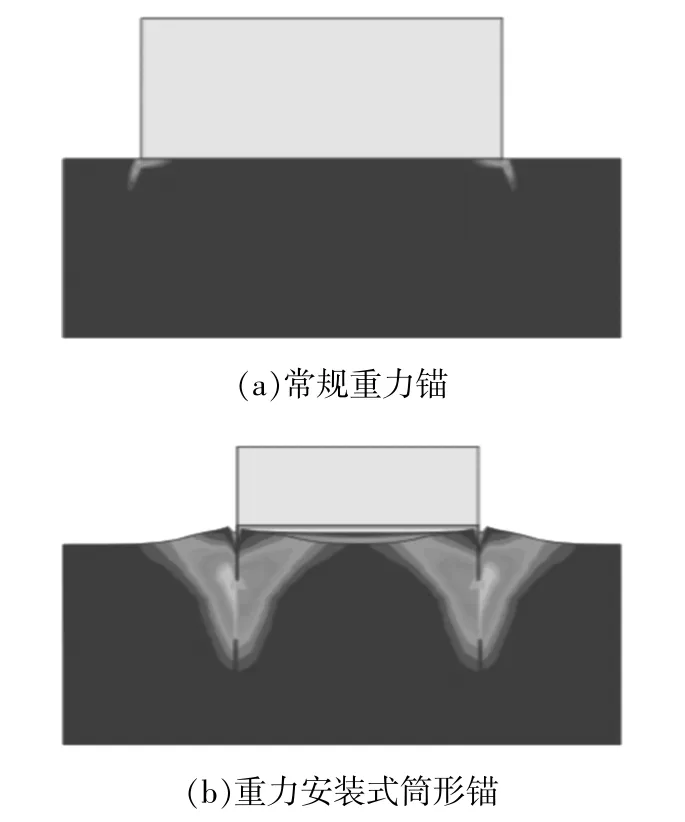
图6 上拔荷载下地基破坏时的塑性变形Fig.6 The plastic zone under pullout loading

由图6可知：由于常规重力锚仅与土层表面相接触，土体的塑性应变范围很小，仅有与土体接触面的四周的少量土体产生了塑性区，这说明常规重力锚主要依靠自重抵抗上拔力；当重力安装式筒形锚受到上拔力时，筒形周围斜向上产生楔形体塑性区，且由于土体为砂土，筒形基础的顶面与土体产生了分离，主要为筒形侧壁的摩擦力以及自身的重量抵抗上拔力，这种破坏模式一般称为不密封破坏模式。

前文计算分析了锚固基础在分别承受水平荷载和上拔荷载时的破坏模式。当锚固基础承受倾斜向上的荷载时，即同时受水平（H）和上拔（V）荷载时，需要考虑采用H-V耦合效应对承载力的影响[15]。考虑H-V耦合效应时，有限元的计算模型不变，但加荷方式发生变化。本文采用常用的Swipe加载方法进行计算。首先，沿X方向采用位移控制法施加荷载，直至达到极限承载力；然后，保持X方向的位移不变，沿Y方向施加位移荷载，直至达到极限承载力。得到的加载轨迹可作为基础的破坏包络线[23]。采用上述方法得到的两种基础的H-V破坏包络线如图7所示。

图7 两种锚型的H-V破坏包络线Fig.7 The failure envelope of two kinds of anchor

由图7可知：由于重力安装式筒形锚可以调动更大范围内地基土的承载力，其水平向承载力超过2 500 t，满足浮式风机的承载要求；常规重力锚的水平承载力为1 100 t左右，重力安装式筒形锚的水平承载力为常规重力锚的2倍以上；由于上部重力块的重量较大，重力安装式筒形锚H-V破坏包络面的形状更加接近于圆形而不是常见的椭圆形。

4 结论

本文针对高渗透性砂土提出了一种重力安装式筒形锚，采用CEL法模拟了重力安装式筒形锚的贯入。利用拉格朗日法分别计算了重力安装式筒形锚和常规重力锚的水平和抗拔承载力，同时采用Swipe加荷方式得到了两种类型锚固基础的H-V破坏包络面。

①采用重力块将筒形基础贯入至土体一定的深度是可行的。重力安装式筒形锚可以作为土体渗透性较大，吸力锚安装存在困难条件下的一种选择。

②由于存在一定的入泥深度，重力安装式筒形锚在承载过程中将形成更大范围的塑性区，因此对具有几乎相同重量的重力安装式筒形锚和常规重力锚，重力安装式筒形锚的水平承载力可以达到常规重力锚的2倍。

③对于砂土中的筒形基础，其上拨破坏为不密封模式。在这种破坏模式下，重力安装式筒形锚在复合加载模式下的H-V破坏包络面的形状更加接近于圆形。

④重力安装式筒形锚可以作为粗砂质海底条件下浮式风机锚固基础的一种选择。