准零刚度隔振平台的冲击响应及能量分析
2024-01-22刘彦琦顾黄森宋春芳汪新邓二杰王友会
刘彦琦,顾黄森,宋春芳,汪新,邓二杰,王友会
(1. 北京市科学技术研究院 城市安全与环境科学研究所,北京 100054; 2. 江南大学 机械工程学院 江苏省食品先进制造装备技术重点实验室,江苏无锡 214122)
近年来,非线性隔振理论及应用迅猛发展[1],准零刚度隔振系统作为一种新兴的非线性低频隔振技术,改变了线性系统隔振的传统观念。准零刚度隔振系统是由正负刚度结构并联组成,正刚度结构可以提供承载能力,负刚度结构主要用于降低系统的总刚度,使整个隔振系统的总刚度值接近于零,即为准零刚度。高静低动刚度的准零刚度隔振器具有优良的低频隔振性能,其动态特性、隔振性能受到广泛关注,主要聚焦于非线性高静低动系统在谐波激励下的隔振性能研究[2-4]。Hao等[5]设计了一种高静、低动刚度可调的六自由度正交隔振系统,并通过理论与实验研究了其隔振性能。刘彦琦等[6]研究了耦合线性吸振器的准零刚度隔振系统的隔振性能。姚国等[7]对X型准零刚度隔振器的隔振特性进行了研究分析。赵权等[8]研制了一种空间占比小、安装方便的准零刚度车载隔振系统并研究了其低频隔振性能。然而,冲击载荷普遍存在工程中,准零刚度隔振平台的冲击响应分析同样重要。
国内外的学者对冲击响应进行了一定的研究。任晨辉等[9]提出了一种由多层负刚度余弦形曲梁连接构成的新型高性能舰船设备冲击防护装置,给出了余弦形曲梁横向压载下力-位移关系解析表达并优化了模型。Tang等[10]研究了具有高静低动刚度特性的非线性隔振器在半正弦和圆形阶跃冲击激励下的动态特性,并提出了3种评价系统缓冲性能的指标。高鹏等[11]设计了一种八连杆抗冲击隔离器,并通过模拟仿真分析了系统的抗冲击性能。Ledezma-Ramirez等[12]研究了一种用于冲击隔振的非线性低动力刚度实验装置,并分析了系统冲击响应。Shekhar等[13]研究了在瞬态基础冲击激励下几种非线性隔振器的冲击性能。Yan等[14]研究了带负电阻电磁并联阻尼的非线性隔振器的冲击隔振性能。Huang等[15]研究了欧拉梁作为负刚度调节器的非线性隔振系统的抗冲击特性,分析了刚度对系统冲击响应的影响。
本文针对准零刚度隔振平台,研究了准零刚度隔振系统冲击响应和系统能量损耗特性。数值分析了系统在冲击激励下的时域响应,并与相应的线性系统进行了对比分析。进一步分析了阻尼和结构参数对系统缓冲性能的影响,以系统能量损耗速度作为缓冲性能评价指标。
1 准零刚度隔振平台模型
通过碟形弹簧与螺旋弹簧并联构成压杆式准零刚度单元,如图1a)所示。由3个压杆式准零刚度单元铰接构成锥形支柱,准零刚度隔振平台由承载平台及4个锥形支柱组成,如图1b)所示。
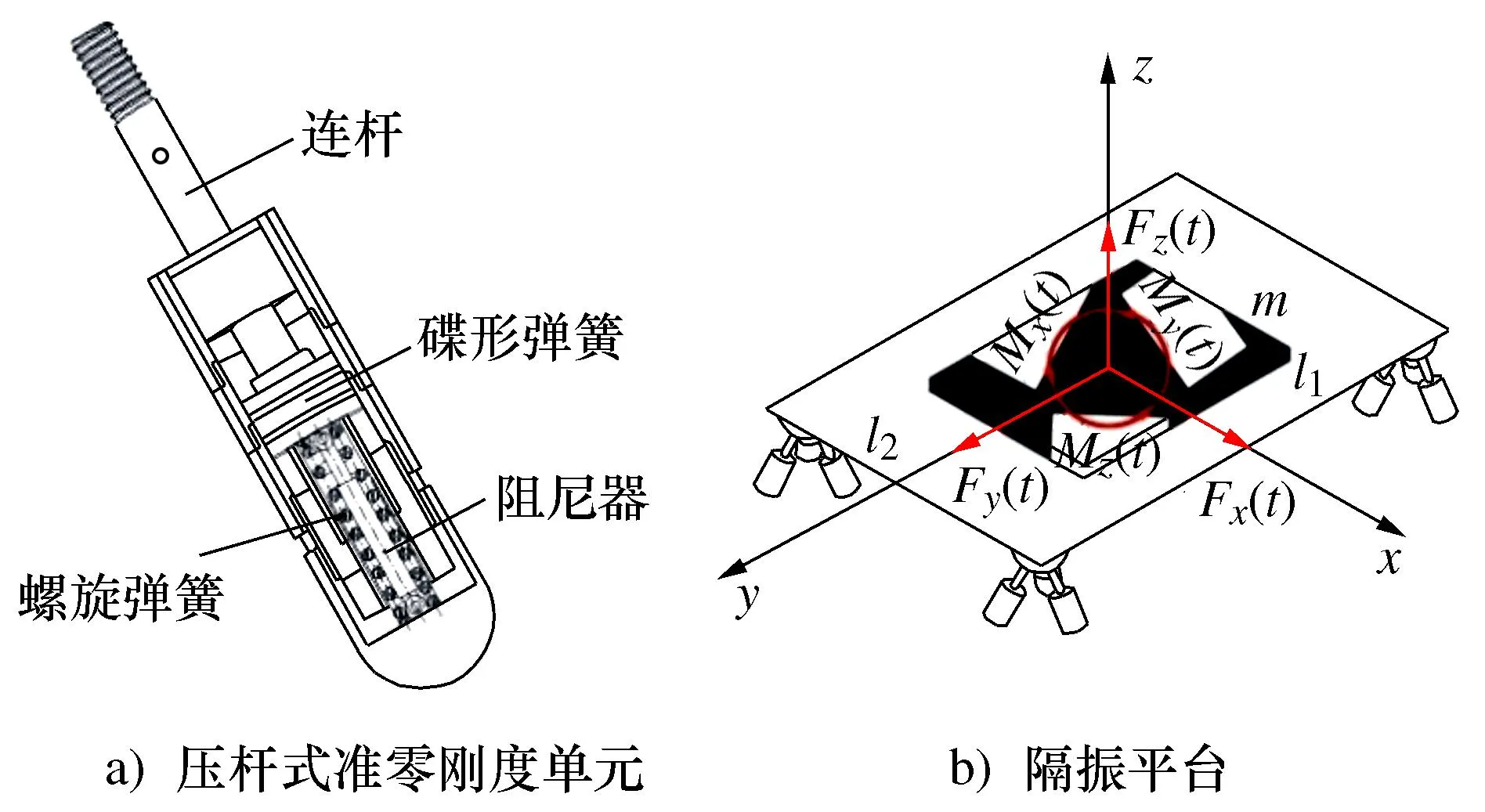
图1 准零刚度隔振平台结构示意图Fig.1 Structure of quasi-zero stiffness vibration isolation platform
碟形弹簧初始处于预压缩状态,其结构示意图如图2所示,当其受到外激励时,碟形弹簧提供了负刚度,用于抵消正刚度,从而降低系统的动刚度,实现系统准零刚度。锥形支柱的3个压杆式准零刚度单元均匀布置,在静平衡状态时,其与竖直方向的夹角为φ,其中锥形支柱受力分析如图3所示。

图2 碟形弹簧结构示意图Fig.2 Structure of disc spring
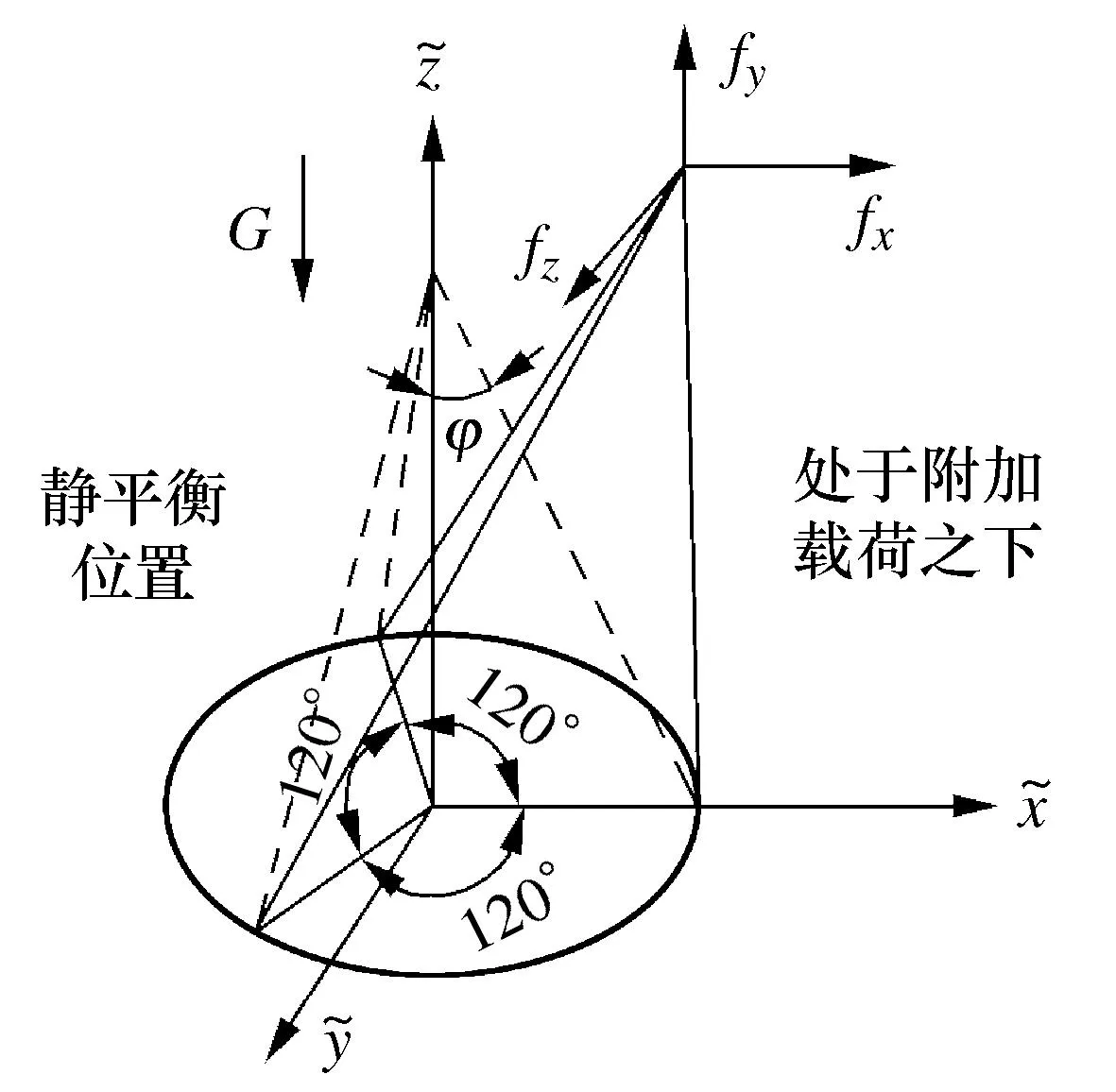
图3 锥形支柱受力分析图Fig.3 Force analysis of conical prop
承载平台质心受到附加荷载作用时,准零刚度隔振平台产生的回复力(Fx,Fy,Fz,Mx,My,Mz)[16-19]表达式为:
(1a)
(1b)
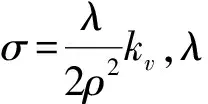
2 动力学方程
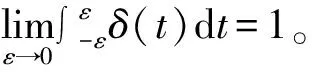
则系统的非线性动力学方程为

(2)
式中:M=diag{m,m,m,Ix,Iy,Iz};c为线性黏滞阻尼系数矩阵;u为承载平台中心受到激励作用时各个自由度方向产生的位移,u={x,y,z,θx,θy,θz}T;Ft为冲击激励;Fr为回复力。
由冲量定理可知:当冲击持续时间t极短时,平台尚未发生任何位移,但速度可以突变,随着冲击激励的消失,平台运动问题可转变为初始位移为0,初始速度最大的自由振动问题[20]。
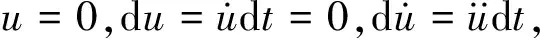
(3)
将式(3)在[-ε,ε]内积分,得到冲击激励作用后的速度增量为H0/M,即在冲击激励消失后,初始运动条件为
(4)
在脉冲激励结束后,系统在式(4)表示的初始扰动下做自由振动。
通过将准零刚度系统中所有非线性因素去除从而可以得到相对应的线性系统,其中ωnz为相应的线性平台z方向的固有频率,则平台动力学方程可转化为:
(5)
其中:
u′=[x′,y′,z′,θx,θy,θz]T,
ζ=diag{ζ1,ζ2,ζ3,ζ4,ζ5,ζ6},
F′r=[F′x(u),F′y(u),F′z(u),M′x(u),M′y(u),M′z(u)]T,
3 冲击响应分析
准零刚度隔振平台结构参数及平台初始运动参数见表1,冲量大小为隔振平台及被隔振物体质量的10%。

表1 隔振平台及初始运动参数Tab.1 Vibration isolation platform and initial motion parameters
通过求解式(5),得到准零刚度隔振平台在冲击激励下的时域位移响应,对比展示了准零刚度隔振平台与相应线性系统的冲击位移响应,如图4所示。
由图4可知:在冲击激励下,系统在经过一段时间后位移趋于0。此外,准零刚度隔振系统的位移幅值高于相应的线性系统,但是在系统衰减过程中,准零刚度系统所用的衰减周期数远远低于线性系统。因此,若从位移幅值的角度评价,准零刚度系统缓冲效果不如线性系统,若从系统衰减过程中所需周期数判断,则准零刚度系统远优于线性系统。
阻尼对准零刚度系统冲击响应的影响如图5所示,随着系统阻尼增大,系统位移响应幅值降低,并且系统衰减所需时间减少,所需的周期数降低。

图5 不同阻尼下系统位移响应Fig.5 Displacement response under different dampings
4 系统能量转换
在冲击激励的情况下,系统在冲击的极短过程中并未发生位移,没有能量损耗,但是产生了较大的初速度,所以冲击能全部转化为系统的动能,冲击结束后系统做自由振动,在自由振动过程中,冲击能逐渐转化为系统动能、势能以及运动过程中的能量损耗。设冲击能为J1,系统动能为J2,系统势能为J3,自由振动过程中的能量损耗为J4,则系统自由振动过程中能量损耗占比为
(6)
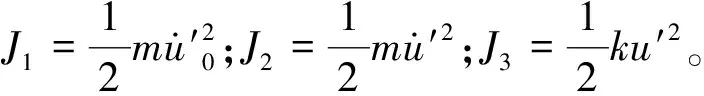
式(6)可用于评价系统的缓冲性能,若系统能量损耗越快,则系统缓冲性能越好。
不同阻尼情况下,准零刚度隔振平台系统能量损耗占比曲线如图6所示。

图6 不同阻尼下系统的能量损耗占比曲线Fig.6 Energy loss ratio curve under different dampings
由图6可知:准零刚度隔振系统的能量损耗占比总体上随着时间的持续迅速增大经过波动而后逐渐趋近于1,并且随着阻尼的增加,能量损耗占比曲线的变化梯度越来越大,说明增大阻尼有助于提升系统的缓冲能力。在能量损耗占比曲线趋近于1的过程中,曲线会出现峰谷,这可能是由于非线性系统的运动不稳定性导致的。在增大阻尼的过程中,曲线峰谷位置的值分别从0.78、0.77、0.90、0.42、0.65、0.66增大至0.98、0.98、1(峰谷消失)、0.85、0.95、0.96,峰谷不断减小,且当阻尼增大到一定程度时,峰谷会直接消失。
图7为不同刚度比λ时系统六自由度方向能量损耗占比情况。除z自由度方向之外,其他5个自由度能量损耗曲线均出现峰谷,并且x、y自由度方向,只在刚度比λ=1时,出现峰谷现象。在非峰谷区域,在每个自由度上,系统在不同刚度比下的能量损耗曲线非常的接近,即刚度比对系统能量损耗曲线的影响不显著。在峰谷区域,刚度比对曲线峰谷具有一定的作用,随着刚度比的减小曲线峰谷处的值分别从0.95、0.94、0.71、0.81、0.88增大至0.98、0.98、0.85、0.96、0.95,峰谷不断减小,当刚度比减小到一定程度时,峰谷会趋于消失。

图7 不同刚度比λ下系统能量损耗占比曲线Fig.7 Energy loss ratio curve under different stiffness ratio λ
不同倾斜角φ的情况下,系统6个自由度方向的能量损耗占比曲线如图8所示。与刚度比相似,在非峰谷区域,在给定的3组倾斜角度的工况,系统能量损耗占比曲线非常接近;即在每个自由度上,倾斜角对系统能量损耗占比的影响不显著。倾斜角的变化只会对系统损耗能量占比曲线的峰谷造成一定影响,增大倾斜角会加深曲线的峰谷。
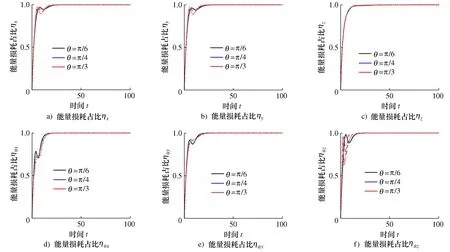
图8 不同倾斜角φ下系统的能量损耗占比曲线Fig.8 Energy loss ratio curve of the system at different inclination angles φ
5 结论
1) 在冲击激励下,准零刚度系统的位移响应幅值高于线性系统,但准零刚度系统位移响应的衰减速度快于线性系统,衰减所需的周期数少于线性系统;增大阻尼会使系统的位移响应幅值降低,衰减速度加快,衰减所需周期数减少。
2) 增大阻尼的过程中会使能量损耗占比曲线坡度变陡,说明增大阻尼有助于提升系统缓冲性能,并且在增大阻尼的过程会使曲线的峰谷逐渐减小甚至消失。
3) 除z自由度方向之外,其他5个自由度能量损耗曲线均出现峰谷。在非峰谷区域,刚度比对系统每个自由度的能量损耗曲线的影响均不显著。在峰谷区域,刚度比对曲线峰谷具有一定的作用,减小刚度比能减小曲线的峰谷,当刚度比减小到一定程度时,峰谷会趋于消失。
4) 倾斜角的变化只会对系统损耗能量占比曲线的峰谷带来一定影响,增大倾斜角会加深曲线的峰谷;在非峰谷区域,系统倾斜角φ对能量损耗占比的影响不显著。
